基于三维模型的改进正则化ERT成像算法

李守晓，王化祥，范文茹，张玲玲

基于三维模型的改进正则化ERT成像算法

李守晓1，王化祥1，范文茹2，张玲玲3

(1. 天津大学电气与自动化工程学院，天津 300072；2. 中国民航大学航空自动化学院，天津 300300；3. 天津大学理学院，天津 300072)

电阻层析成像(ERT)通过对被测场边界注入电流，测量被测场电压变化，重建物场内电导率．针对ERT成像分辨率低，提出一种基于三维模型的改进Tikhonov迭代电阻成像算法．针对Tikhonov正则化参数选择问题，提出基于同伦映射的方法，并利用非线性函数Sigmoid调节正则化参数，以获得的图像灰度值作为Tikhonov迭代法的初始值进行迭代，重建敏感场图像．仿真及实验结果表明，该方法有效地改进了ERT图像质量．

电阻层析成像；图像重建；正则化；同伦映射

电阻层析成像[1](electrical resistance tomography，ERT)技术是基于边界电压测量值反映物场内部电导率分布的变化[2]．由于该技术具有非侵入、无辐射、响应快、结构简单以及成本低廉等优点，在石油、化工等领域具有广阔的应用前景[3]．

ERT成像算法包括非迭代算法和迭代算法[4]．非迭代算法包括线性反投影、Tikhonov正则化算法、基于截断奇异值分解的直接算法；迭代算法包括landweber迭代算法、牛顿-拉夫逊迭代算法以及共轭梯度迭代算法．线性反投影算法虽然简单快速，但该算法成像精度较低．landweber迭代算法与最速梯度下降法类似，但其收敛性比较差[5]．牛顿-拉夫逊迭代算法虽然收敛快但计算量较大且具有局部收敛的缺点．Tikhonov正则化算法的成像质量主要依靠正则化参数的选择．最优的正则化参数将得到质量高的图像．但该种算法中正则参数一般不易确定，通常需要通过实验观测确定，而且确定的参数并非最优值.

为了提高正则化方法的效率，减少由于试探正则化参数所带来的不便，笔者基于同伦映射，构造了同伦映射函数，将Tikhonov正则化方法引入了一种连续可调的正则化参数修正方法，节省了时间．随着迭代的进行，采用固定点正则化参数修正，用所得图像灰度值作为Tikhonov迭代法的初始值进行成像，提高成像质量．

1 ERT系统基本原理

为电阻层析成像的反问题求解，即通过已经测量的电压值反求被测管道截面的电导率分布情况．电阻层析成像线性模型为[6]

式中：g为电导率分布矢量，在图像重建中代表图像灰度值；z为电压矢量，即电导率变化引起边界的电压变化；S为灵敏度矩阵．ERT反问题的求解即由已知的测量电压z求解未知g的过程．电阻层析成像的不适定性直接影响成像质量．运用正则化的方法可以使求解更稳定、成像更精确．

2 算 法

2.1Tikhonov正则化方法

Tikhonov方法是ERT中求解反问题最常用的方法之一．Tikhonov正则化的基本思想是通过约束解的范数以保证解不发散．其最小化目标函数为

式中：μ为正则化参数；L(g)称为正则化函数．应用牛顿-拉夫逊迭代法，标准的迭代公式为

式中I为nn×单位阵．将最小化目标函数变为

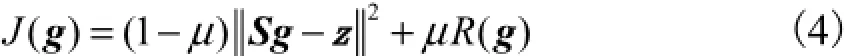
采用牛顿-拉夫逊迭代可得到改变的Tikhonov正则化迭代形式

2.2同伦映射

设X和Y是Rn的非空子集，f，p：X→Y是光滑映射．如果对任意α∈[0,1]，(α,x)∈[0,1]×X都成立，H(α,x)=(1-α)f(x)+αp(x)∈Y 则称光滑映射H:[0,1]×X→Y是f和p之间的一个线性同伦[7]，α为同伦参数．

根据定义，若需要求解的原方程为

基于同伦映射，构造同伦函数

式(7)满足

由式(7)可知，α为同伦参数，α∈[0,1]．当α= 0时式(7)等价于式(6)．若从式(7)出发，在求解的过程中通过连续减少α的值，最终将求得式(6)的解．由于H(α,x)≥0，所以可按最优拟合的原则将式(7)的求解转化为无约束最优化问题，即

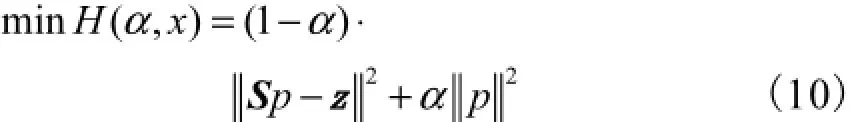
应用正则化方法进行求解

将式(11)应用于牛顿-拉夫逊迭代将得到与式(5)相似的迭代形式，其中α与μ有着相似的关系．由于同伦映射可跟踪α的求解，因此可解决正则化参数μ难以确定的问题．

2.3改进正则化算法

对于正则化参数的确定，目前已发展了Arcangeli和误差极小化等，上述方法的共同点是需要预先估计原始数据的误差水平．但在过程参数检测中，被测参数分布较复杂，先验知识较难获取．传统试探的方法虽然理论上能获得最优的μ值，但计算量大．针对这种情形，本文中提出改进的正则化方法．由同伦参数与正则化参数相似性，可以采用同伦路径追踪的方法确定正则化参数μ．同伦路径追踪有很多方法，如高阶插值预估-Newton校正算法和欧拉预估-Newton校正算法等．因正则化参数介于[0，1]之间，考虑到同伦映射，同伦参数需要从1或接近l的数逐渐逼近0．参考人工神经元网络的非线性作用函数，即Sigmoid函数，引入连续同伦参数调整公式，即

式中：N为迭代次数，当a=1，b=0时为典型的Sigmoid函数[8]．式(12)中的同伦参数即是正则化参数．

对于本文的问题经过多次实验，a取0.5，b为[-10，10]之间的实数，本文b=-0.5．由于同伦参数的跟踪变化是连续的，可以保证迭代稳定地进行．

引入原始图像与重建图像的相关系数[9]

式中：g*是被测区域内的真实电导率分布；g是电导率计算值；g*和g分别是g*和g的平均值．由于式(12)随着N值的越来越大，同伦参数的变化很缓慢，算法效率低．故在图像最大相关系数下降5%时，μ值取0.001，将由式(13)的算法所成图像作为式(5)迭代图像灰度初始值，提高算法的实时性[10]和图像质量．

改进正则化方法采用式(5)的迭代形式，其中μ值选取采用分段函数形式为

3 实验与仿真结果

为验证改进正则化方法的有效性，通过建立三维模型，分别运用Tikhonov正则化方法(TIK)、改进的Tikhonov正则化方法(HTIK)和截断奇异值分解的直接方法(TSVD)对3种电导率分布模型进行仿真[11]与实验．

3.1ERT仿真实验

采用Matlab软件和有限元软件COMSOL求解正问题．首先采用有限元软件COMSOL建立三维模型，并用其剖分网格．采用3种不同电导率分布的三维模型，有限元单元采用四面体单元如图1所示．模型(Ⅰ)共有13,885个节点，7,068个四面体单元；模型(Ⅱ)共有14,699个节点，7,711个四面体单元；模型(Ⅲ)共有15,703个节点，8,434个四面体单元．ERT的测量方式选择相邻驱动模式，电导率对比度1∶2．

反问题求解采用方形网格，网格数为812个，分别运用TIK算法、TSVD算法和HTIK算法进行成像．根据经验选择能够得出理想图像的μ值．在仿真中对TIK算法选择不同μ值，模型(Ⅰ)的μ值选为10-6，模型(Ⅱ)和模型(Ⅲ)的μ值选为0.02．迭代次数都选为20次，进行成像．表1给出了3种算法的成像结果，成像图选取3维模型的中间截面如图2所示．可以看出HTIK法成像效果明显好于TIK法和TSVD法．

图1 ERT三维模型Fig.1 3D model of ERT

图2 三维模型截面示意Fig.2 Section of 3D model

表1 仿真模型和成像效果Tab.1 Simulation models and reconstructed images

由于仿真中实际电导率分布已知，所以采用图像的相关系数对重建图像质量进行评判．对3种不同电导率分布模型分别采用TIK和HTIK进行成像比较．图3为取50次迭代所成图像的相关系数．从图3中可以看出HTIK的图像相关系数更高．TIK方法要耗费大量的时间进行μ值的选择，而且图像最大相关系数低于HTIK．

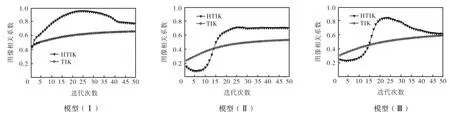
图3 模型的图像相关系数曲线Fig.3 Curves of correlation coefficient of models

对反问题采用不同数量的网格剖分[12]，分别对两种成像算法的计算时间进行比较(计算机配置：Intel 酷睿2双核P,7350，主频2.0,GHz，内存2.0,GB，操作系统为Windows7)，如表2所示．可以看出随着逆问题网格剖分数量的增加，HTIK所花时间比TIK略少．由于传统TIK算法对μ值的选择要进行多次实验观测确定，所以实际上HTIK方法节省了大量时间．

表2 不同算法图像成像实时性比较(50次迭代)Tab.2 Comparison of different algorithms in terms of computation time(iteration 50)

3.2ERT实验结果

图4 ERT成像实验Fig.4 ERT imaging experiment

电阻成像实验系统如图4所示，激励电流小于5,mA，激励频率范围10,kHz～1,MHz(实验激励频率为100,kHz)，激励模式为相邻激励，采用相邻测量的测量模式，解调方式为数字相敏解调，测量信噪比60,dB，数据采集速度为120帧/s，每幅含208个数据，USB2.0数据接口，上位机软件采用VC6.0的界面，运用OpenGL进行图像显示．水槽直径为200,mm；16个电极为直径10,mm的圆形不锈钢电极；溶液为NaCl溶液；成像物体为直径25,mm有机玻璃棒；1,m长单层屏蔽电缆．

将NaCl加入水中测得溶液电导率为0.2,s/m，运用实验装置进行实验．实验模型参照仿真模型，有机玻璃棒放在盐水里的分布见表3．分别采用HTIK(25次迭代)、TIK(100次迭代)、TSVD 3种方法进行成像．其中TIK中的正则化参数μ根据经验选择，模型(Ⅰ)选为10-6、模型(Ⅱ)(Ⅲ)选为0.02．成像结果如表3所示．

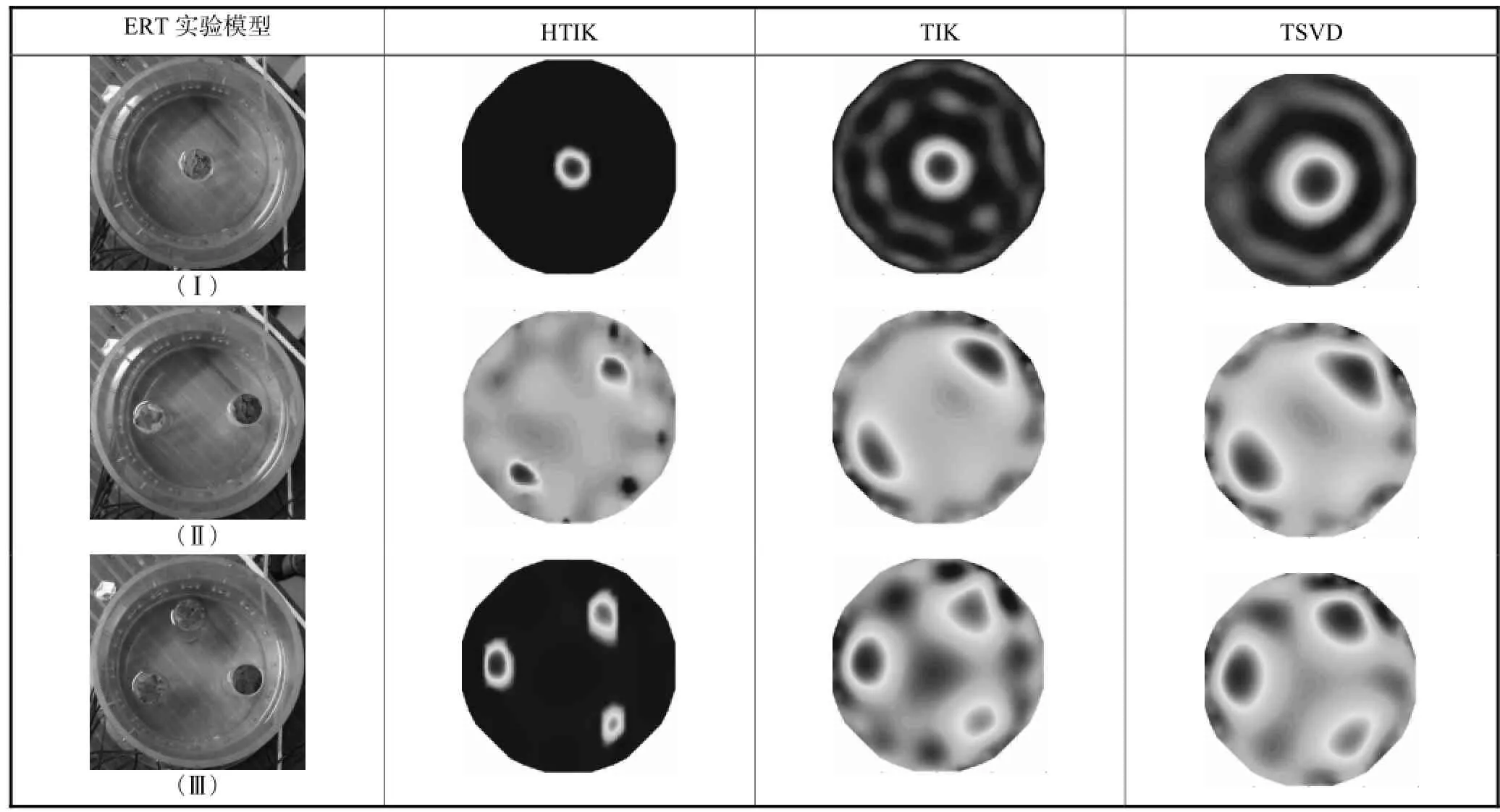
表3 模型和实验成像效果Tab.3 Models and reconstructed images for experimental results

在实际的测量中，由于测量误差以及仪器本身的误差导致实验数据与仿真有差异[13]．由表3可以看出HTIK成像场域更加均匀，离散相更接近真实分布．HTIK成像效果优于TIK和TSVD．

4 结 语

提出了一种改进的Tikhonov正则化方法用于ERT成像．基于同伦映射方法对正则化参数进行连续调节，然后用所得图像灰度值作为Tikhonov迭代法的初始值进行成像，提高成像质量．同传统的Tikhonov正则化方法比较，HTIK具有成像质量高，花费时间少的优点，通过仿真和实验证明了图像重建的可行性．

［1］ Dickin F，Wang Mi. Electrical resistance tomography for process applications[J]. Meas Sci Technol，1996，7(3)：247-260.

［2］ Zlochiver S，Freimark D，Arad M，et al. ParametricEIT for monitoring cardiac stroke volume[J]. Physiol Meas，2006，27(5)：139-146.

［3］ Hu Li，Wang Huaxiang，Zhao Bo，et al. A hybrid reconstruction algorithm for electrical impedance tomography[J]. Meas Sci Technol，2007，18(3)：813-818.

［4］ 王化祥，范文茹，胡 理. 基于GMRES和Tikhonov正则化的生物电阻抗图像重建算法[J]. 生物医学工程学杂志，2009，26(4)：701-705.

Wang Huaxiang，Fan Wenru，Hu Li. A hybrid reconstruction method in electrical impedance tomography based on GMRES and Tikhonov regularization[J]. Journal of Biomedical Engineering，2009，26(4)：701-705(in Chinese).

［5］ 彭黎辉，陆 耿. 电容成像图像重建算法原理及评价[J]. 清华大学学报：自然科学版，2004，44(4)：478-484.

Peng Lihui，Lu Geng. Image reconstruction algorithms for electrical capacitance tomography：State of the art[J]. Journal of Tsinghua University：Science and Technology，2004，44(4)：478-484(in Chinese).

［6］ 王化祥，唐 磊，闫 勇. 电容层析成像图像重建的总变差正则化算法[J]. 仪器仪表学报，2007，28(11)：2014-2018.

Wang Huaxiang，Tang Lei，Yan Yong. Total variation regularization algorithm for electrical capacitance tomography[J]. Chinese Journal of Scientific Instrument，2007，28(11)：2014-2018(in Chinese).

［7］ 王则柯. 同伦方法引论[M]. 重庆：重庆出版社，1990.

Wang Zeke. An Introduction to Homotopy Methods[M]. Chongqing：Chongqing Publishing House，1990(in Chinese).

［8］ 崔 凯，杨国伟，李兴斯. 用同伦方法反演非饱和土中溶质迁移参数[J]. 力学学报，2005，37(3)：307-312.

Cui Kai，Yang Guowei，Li Xingsi. A homotopy method for parameter inversion of solute transport through unsaturated soils[J]. Acta Mechanica Sinica，2005，37(3)：307-312(in Chinese).

［9］ Li Yi，Yang Wuqiang. Virtual electrical capacitance tomography sensor[J]. Journal of Physics：Conference Series，2005，15(1)：183-188.

［10］ Sun Meng，Liu Shi，Lei Jing，et al. Mass flow measurement of pneumatically conveyed solids using electrical capacitance tomography[J]. Measurement Science and Technology，2008，19(4)：1-6.

［11］ Nick P，William R B L. A Matlab toolkit for threedimensional electrical impedance tomography：A contribution to the electrical impedance and diffuse optical reconstruction software project[J]. Meas Sci Technol，2002，13(12)：1871-1883.

［12］ 王化祥，朱学明，张立峰. 用于电容层析成像技术的共轭梯度算法[J]. 天津大学学报，2005，38(1)：1-4.

Wang Huaxiang，Zhu Xueming，Zhang Lifeng. Conjugate gradient algorithm for electrical capacitance tomography[J]. Journal of Tianjin University，2005，38(1)：1-4(in Chinese).

［13］ Fagerberg A，Stenqvist O，Aneman A. Electrical impedance tomography applied to assess matching of pulmonary ventilation and perfusion in a porcine experimental model[J]. Crit Care，2009，13(2)：852-857.

Improved Regularization Reconstruction Algorithm Based on 3D Model for ERT System

LI Shou-xiao1，WANG Hua-xiang1，FAN Wen-ru2，ZHANG Ling-ling3
(1. School of Electrical Engineering and Automation，Tianjin University，Tianjin 300072，China；2. College of Aeronautical Automation，Civil Aviation University of China，Tianjin 300300，China；3. School of Sciences，Tianjin University，Tianjin 300072，China）

Electrical resistance tomography (ERT) is a technique for reconstructing the conductivity distribution inside an inhomogeneous distribution by injecting currents at the boundary ofa subject and measuring the resulting changes in voltage. To improve the poor imaging quality for ERT, an improved regularization reconstruction algorithm(HTIK)based on 3D modelling was presented. In general, the regularization coefficient of Tikhonov iterative algorithm was difficult to choose, homotopic mapping is adopted. A quasi-Sigmoid method is used to adjust the regularization parameter. Thereafter sensitive field image can be reconstructed by deploying the resultant image vector as the initial value of Tikhonov iteration algorithm. Both simulation and experimental results demonstrate that the proposed method can improve imaging quality obviously.

electrical resistance tomography；image reconstruction；regularization；homotopic mapping

TP212

A

0493-2137(2012)03-0215-06

2011-01-22；

2011-04-24.

国家自然科学基金重大国际合作资助项目(60820106002)；国家自然科学基金资助项目(60532020，50937005)；国家高技术研究发展计划(863计划)资助项目(2006BAI O3A00)；天津市自然科学基金资助项目(11JCYBJC06900).

李守晓（1985— ），男，博士研究生，lsxfly@tju.edu.cn.

王化祥，hxwang@tju.edu.cn.