基于排队论的CAN总线消息响应时间建模与分析

陈 曦，刘鲁源，吕伟杰，李 芳

基于排队论的CAN总线消息响应时间建模与分析

陈 曦1，刘鲁源1，吕伟杰1，李 芳2

(1. 天津大学电气与自动化工程学院，天津 300072；2. 中国科学院电工研究所，北京 100190)

CAN总线消息响应时间是评价CAN总线系统实时性高低的重要性能指标之一，与最糟糕响应时间分析关注极端条件下响应时间计算不同，研究了均值意义下的响应时间建模与分析．在分析CAN总线CSMA/CD协议的基础上，建立了消息响应时间的非强占优先级的M/G/1排队模型．针对CAN总线独有的位填充机制，给出了相应的填充位概率分布函数，计算了均值意义下的消息响应时间．将其用于电动汽车的CAN总线消息响应时间均值计算，印证了响应时间的均值远小于最糟糕响应时间．上述结果从排队论角度对CAN总线系统进行了建模，所提供的模型和方法不仅可用于响应时间的计算和分析，也为CAN总线通信系统的设计与优化提供了理论指导．

CAN总线；响应时间；排队论；优先权；填充位

CAN总线消息响应时间(简称响应时间)分析是评价CAN总线系统实时性高低的重要性能指标之一．目前普遍采用的是最糟糕响应时间分析方法[1-4]，该方法是利用上限函数描述CAN总线带冲突检测的载波侦听多路访问协议(CSMA/CD)，给出极端条件下即最糟糕条件下的响应时间．然而响应时间的均值是公认的另外一个反映通信系统性能的重要量化指标[5]，在基于CAN总线的网络控制系统设计与性能评估、可靠性估计等工程中都有应用．笔者根据CSMA/CD协议，把CAN总线视为一个排队系统，建立非强占优先级的M/G/1排队模型，并以此模型为基础分析计算了消息响应时间的均值．

1 基于排队论的CAN总线消息响应时间建模

排队系统由要求得到服务的“顾客”和给予服务的“服务台”2部分构成．如果把消息占据总线进行数据传输视为“服务”，那么因为CAN总线中的节点在消息传输过程中要占据总线，所以可视其为“顾客”，CAN总线提供消息传输的物理介质并依据CSMA/CD协议进行消息传输的仲裁与管理，所以可视其为“服务台”．一个排队系统主要由3部分构成：输入过程、排队规则和服务机构．就由CAN总线构成的排队系统的输入过程而言，通常CAN总线系统中消息是持续不断发送的，所以认为顾客总数是无限的，且设相继顾客到达的间隔时间服从Poisson分布(M)．CAN总线采用CSMA/CD协议进行消息仲裁，简而言之即当低优先级消息发送时高优先级的消息必须等待低优先级消息发送完毕才能发送，高优先级消息发送时低优先级消息不能发送[1]，这符合非强占优先级的服务规则．CAN总线中的消息只有在全部比特位发送完毕之后才可认为传输结束，所以可以把消息的传输时间视为“服务时间”，因为CAN总线消息的传输时间因填充位的不同而呈一定的概率分布[6-7]，所以服务时间是服从一般概率分布G．由于多个CAN节点接在同一条总线上，任意一个时刻只有一个CAN节点的消息可以在总线上传输，所以只有一个服务台(1)．由分析可知CAN总线上消息的传输符合非强占优先级的M/G/1的排队论模型．

因为排队论主要研究统计平衡下的各种性能指标的概率性质，以下将基于排队论模型研究均值条件下的CAN总线消息响应时间．由于消息的传输时间χ和等待时间Wq是统计独立的，所以消息i响应时间的均值为

2 位填充机制与传输时间的概率分布

由于把消息传输时间视为“服务时间”，所以需要求取服务时间即CAN总线消息传输时间概率分布．根据CAN协议[6]，CAN总线采用NRZ码进行编码，为了实现位同步，采用了位填充机制，即发送节点在连续检测到5个相同极性位如11111或00000后就加入一个相反极性位．接收节点在接收消息时会相应地检测相同极性位数，并去除填充位．位填充机制使得总线上实际传输消息位数大于原始的位数．

如果没有位填充，那么一个CAN消息的总长度可以表示为式中：Li是消息中数据的字节数，0≤Li≤8；g是消息中控制位的总位数，标准格式的消息g=34，扩展格式的消息g=54．参与位填充的共有8Li+g位，剩余的包含CRC界定位、应答位、帧结束和帧间隙在内共13位不进行位填充操作．

进行位填充之后，一个消息的总长度为

式中T是填充位的总数．最糟糕响应时间分析考虑最糟糕情况下即填充位T最多时的消息传输时间，此时每隔4位就插入一个相反极性的填充位，因为参与位填充的只有8Li+g位，所以T的最大值为

可知最糟糕情况下一个消息所用的传输时间是

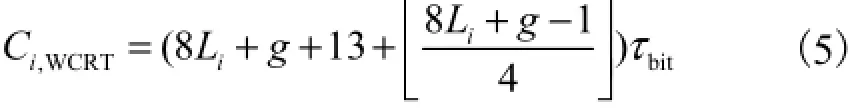
式中τbit是传输一位所需的时间．

事实上因为消息的填充位往往会小于最糟糕情况下的位数，即T值会小于如式(4)所示的最大值，所以消息的传输时间通常会小于式(5)的值，且因各个比特位的排列不同会导致传输时间呈随机变化，因此需要研究传输时间的概率分布函数，即确定排队模型中服务时间的分布类型．

构造一个位填充模型P(Si，m)，该模型由随机生成的5×104个二进制位流序列Si组成，m是位流Si的长度．每个Si满足：①Si中每一位出现0或1的概率相同；②Si中位与位之间相互独立[7-8]．

Si的长度m由不同长度的CAN消息中参与位填充机制的位数而定，根据式(2)，标准格式消息的m取值范围Ms是{5，9，13，17，··，25，29，34，42， 50，58，66，74，82，90，98}，扩展格式消息的m取值范围Ms是{5，9，13，17，··，45，49，54，62，70，78，86，94，102，110，118}，标有下划线的数字对应于0～8个数据字节消息帧中参与位填充机制的位数．

在得到位填充模型P(Si，m)之后，就可以针对不同长度的位流Si统计填充位出现的概率值．图1～图9给出了m分别为54、62、70、78、86、94、102、110、118时(即包含0个、1个、2个、3个、4个、5个、6个、7个和8个数据字节的扩展格式消息)填充位的概率分布(图中位于下方的横坐标)．由于消息传输时间Ci与填充位T满足

所以可得到消息传输时间Ci的概率分布，例如图2中1个数据字节的扩展格式消息当填充位为0时的概率是0.05，即传输时间Ci=(8×1+54+13+0)τbit= 75τbit的概率是0.05．图1～图9中上方的横坐标中列出了传输时间．

由图1～图9计算得到的不同数据字节扩展格式消息传输时间的均值和方差如表1所示．

图1 0个数据字节扩展格式消息填充位和传输时间概率分布Fig.1 Probability distribution of bit-stuffing and transmission time of extended format messages with 0 byte of data

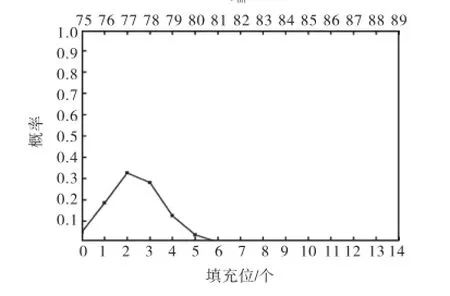
图2 1个数据字节扩展格式消息填充位和传输时间概率分布Fig.2 Probability distribution of bit-stuffing and transmission time of extended format messages with 1 byte of data

图3 2个数据字节扩展格式消息填充位和传输时间概率分布Fig.3 Probability distribution of bit-stuffing and transmission time of extended format messages with 2 bytes of data

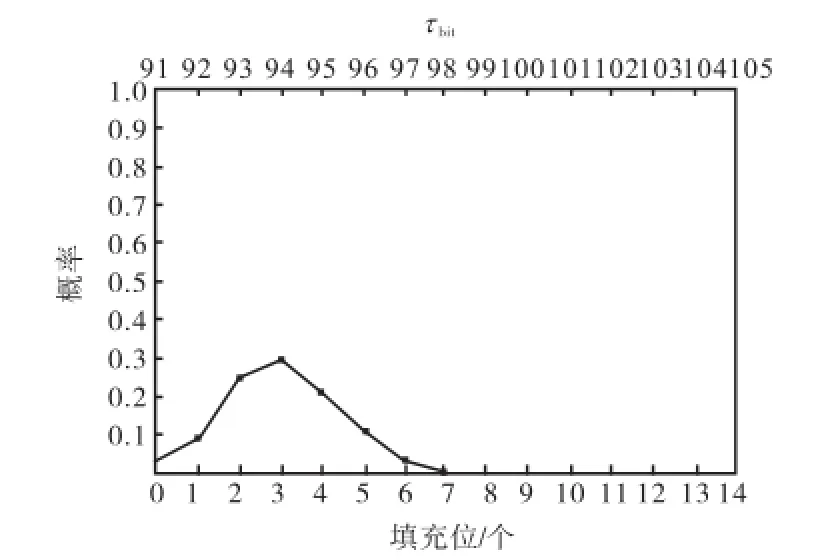
图4 3个数据字节扩展格式消息填充位和传输时间概率分布Fig.4 Probability distribution of bit-stuffing and transmission time of extended format messages with 3 bytes of data

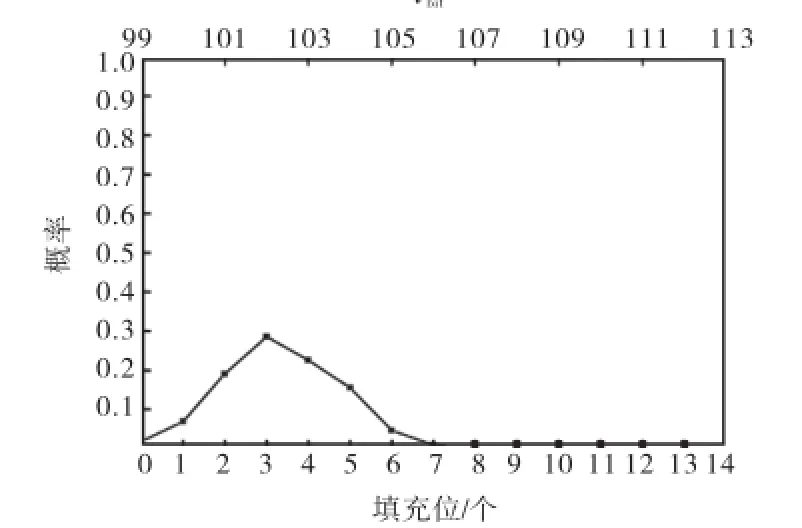
图5 4个数据字节扩展格式消息填充位和传输时间概率分布Fig.5 Probability distribution of bit-stuffing and transmission time of extended format messages with 4 bytes of data

图6 5个数据字节扩展格式消息填充位和传输时间概率分布Fig.6 Probability distribution of bit-stuffing and transmission time of extended format messages with 5 bytes of data

图7 6个数据字节扩展格式消息填充位和传输时间概率分布Fig.7 Probability distribution of bit-stuffing and transmission time of extended format messages with 6 bytes of data

图8 7个数据字节扩展格式消息填充位和传输时间概率分布Fig.8 Probability distribution of bit-stuffing and transmission time of extended format messages with 7 bytes of data

表1 不同数据字节扩展格式消息传输时间的均值和方差Tab.1 Mean and variance of transmission time of extended format messages with different bytes of data

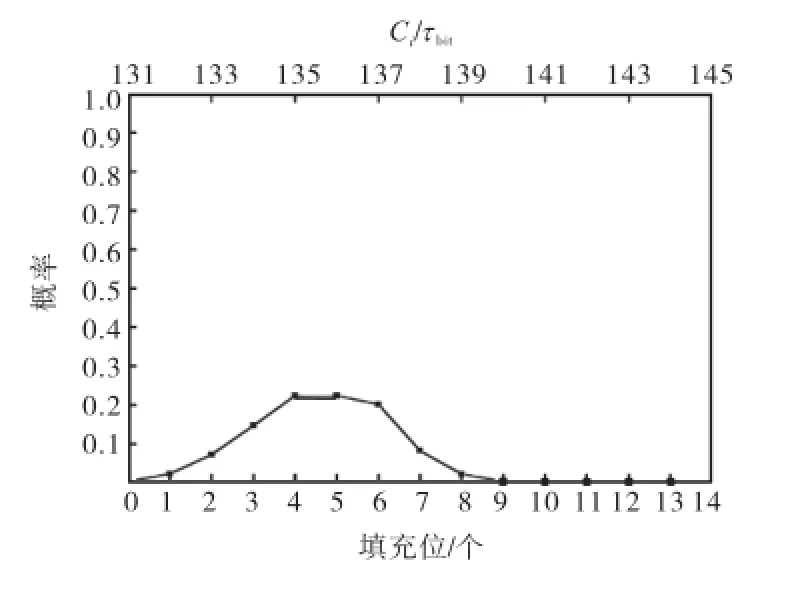
图9 8个数据字节扩展格式消息填充位和传输时间概率分布Fig.9 Probability distribution of bit-stuffing and transmission time of extended format messages with 8 bytes of data

3 CAN总线消息等待时间均值的计算

设某CAN总线消息系统共由k条消息构成，其优先级分别是1，2，··，k，并规定优先级数越小优先级越高，即如果i＜j，那么priority(i)＞priority (j)．消息i(i=1，2，··，k)等待发送时间由3部分构成，即

(1) 当前正在总线上进行传输的消息所需剩余的传输时间S0．

(2) 其他所有已处于发送窗口、优先级为r的消息所需传输时间的总和．设Sr为第r优先级中所有nr个消息的全部传输时间(r=1，2，··，i)．

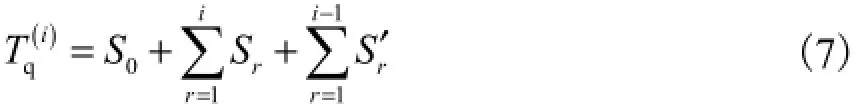
求式(7)的均值，即消息i的平均等待时间为

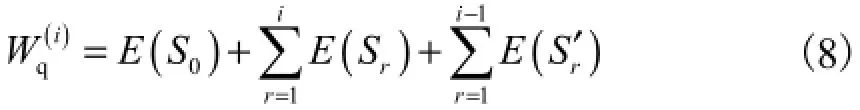
首先计算E(S0)．由于当前正在总线上进行传输的消息r的优先级并不知道，所以用ρr/ρ表示消息r属于第r优先级的概率，消息r的剩余传输时间为Rr，同时考虑到总线处于正在传输状态的概率是ρ，则可得文献[9]指出在一个有k优先级的排队系统中，优先级为r的消息的剩余传输时间的均值为

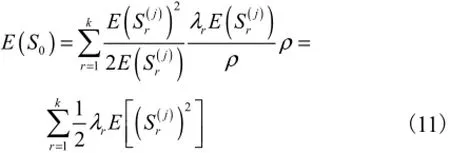
因为其他已处于发送窗口的消息有nr条，所以这些消息的平均传输时间为

式中E(nr)表示平均队长．由于消息的数量和消息的传输时间是统计独立的，且对于任意的概率分布，Little公式都成立[10]，即平均队长为到达速率与等待时间之积，所以式(12)可表示为

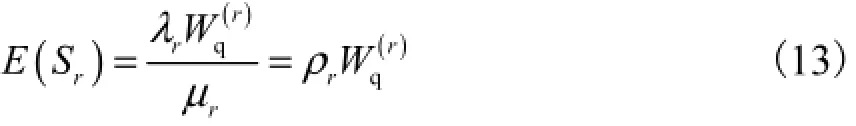
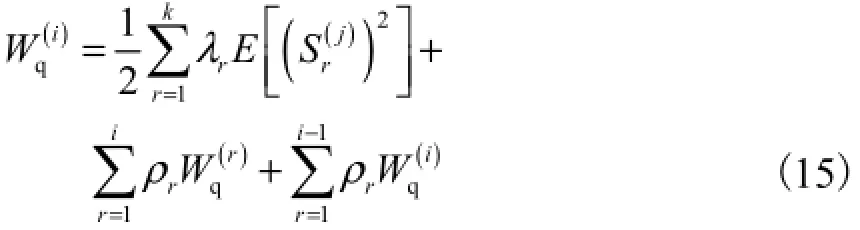
即

式(16)是一个递推公式，考虑到ρ0=0，可得优先级为1的消息等待时间为

由式(16)可得优先级为2的消息等待时间为

用数学归纳法[11]证明满足

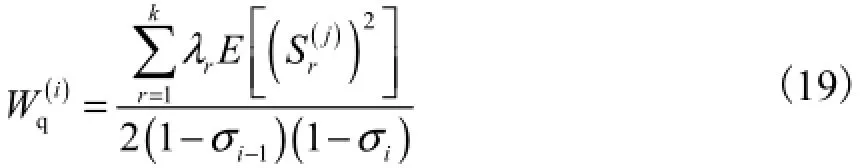
将式(19)代入式(15)可得

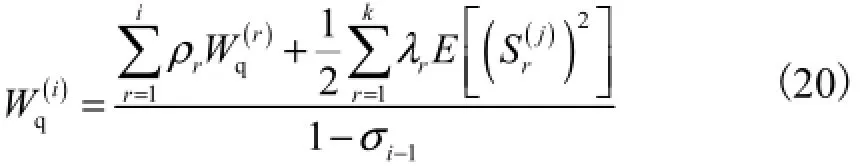
比较式(16)和式(20)可得

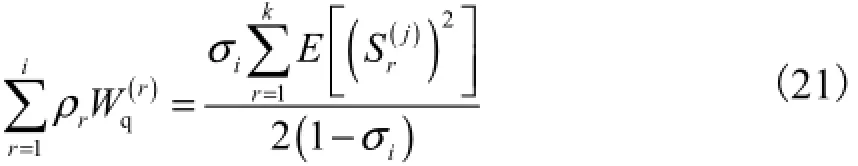
由式(16)可得

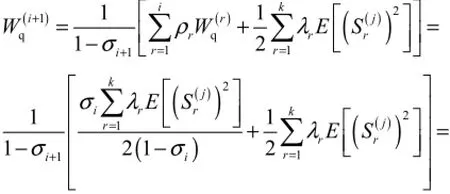
即式(19)在i+1时也成立，由此可证消息i的等待时间为

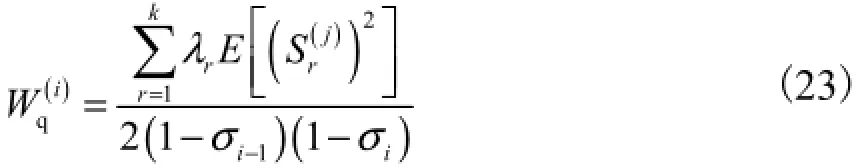
4 计算实例

将第3节论述方法用于CAN消息响应时间的计算．取电动汽车消息模型[11]如表2～表7所示，比特率为250,kb/s，即τbit=4,µs．利用式(22)计算得到的消息等待时间、响应时间均值如表8所示，由文献[1-4]计算的最糟糕响应时间也列在表8中．

由表8可知消息的等待时间随优先级的降低而增大，这是符合客观规律的，因为消息优先级越低，意味着此消息需等待更多、更高优先级消息的概率增大，即式(8)等号右侧后两项的数值在增大，必然会造成等待时间均值的增大．全部消息的响应时间的均值都小于最糟糕响应时间，这与实际相符，因为最糟糕响应时间计算的是极端条件下的响应时间最大值，其值必然要远远大于响应时间的均值．此外最糟糕响应时间和响应时间均值之间的差别随优先级的降低而不断增大，如优先级1的消息，其最糟糕响应时间是消息响应时间均值的2.3倍，而优先级为40的消息即最低优先级消息的最糟糕响应时间是消息响应时间均值的39.7倍．

为了考察消息响应时间均值随总线负载率变化的规律，采用了改变CAN总线的比特率τbit来改变总线负载率，观察消息响应时间变化情况的方法．根据文献[12]，τbit依次设定为125,kb/s、250,kb/s、500,kb/s、800,kb/s、1,Mb/s，相应的网络负载率为71.84%、35.92%、17.96%、11.23%、8.98%，图10是优先级分别为1、20、40的消息响应时间均值变化情况．从图10中可以看出优先级越低，消息响应时间随总线负载率增长而变化的幅度也越大，如优先级为1的消息在负载率为71.84%下的响应时间均值是负载率为8.98%下的10.32倍，而同样条件下优先级为40的消息变化倍数为21.29．从图10中也可以看出在负载率不大于35.92%的情况下，消息响应时间的均值与总线负载率近似成线性变化，而当负载率大于35%时，如图10所示，各优先级的消息响应时间陡然增大．

表2 主控制器消息(节点号1，共12个消息)Tab.2 Messages of main controller(Node1，12 messages)

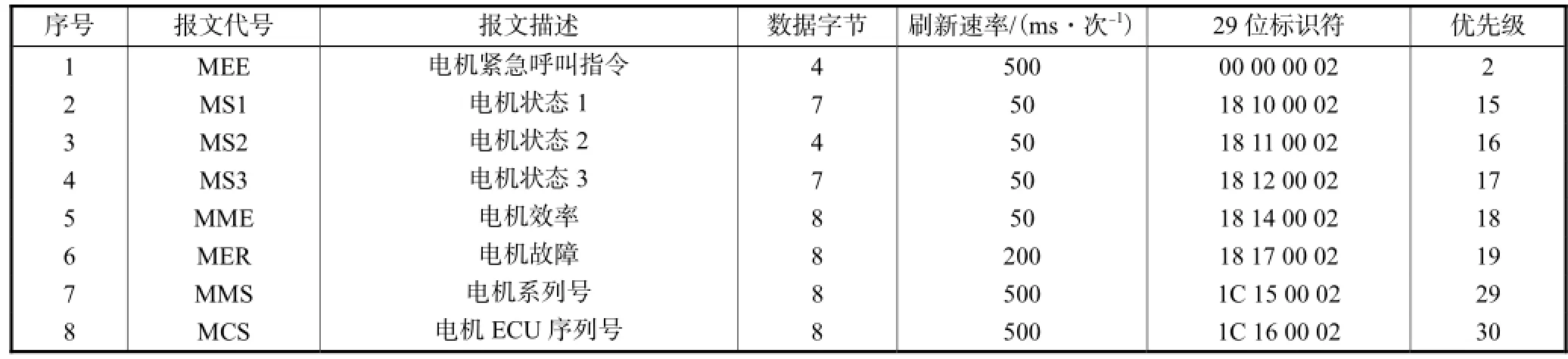
表3 电机ECU消息(节点号2，共8个消息)Tab.3 Messages of motor ECU(Node2，8 messages)

表4 回馈制动ECU消息(节点号4，共3个消息)Tab.4 Messages of regenerative braking ECU(Node4，3 messages)

表5 车载记录仪消息(节点号5，共4个消息) Tab.5 Messages of recorder (Node5，4 messages)

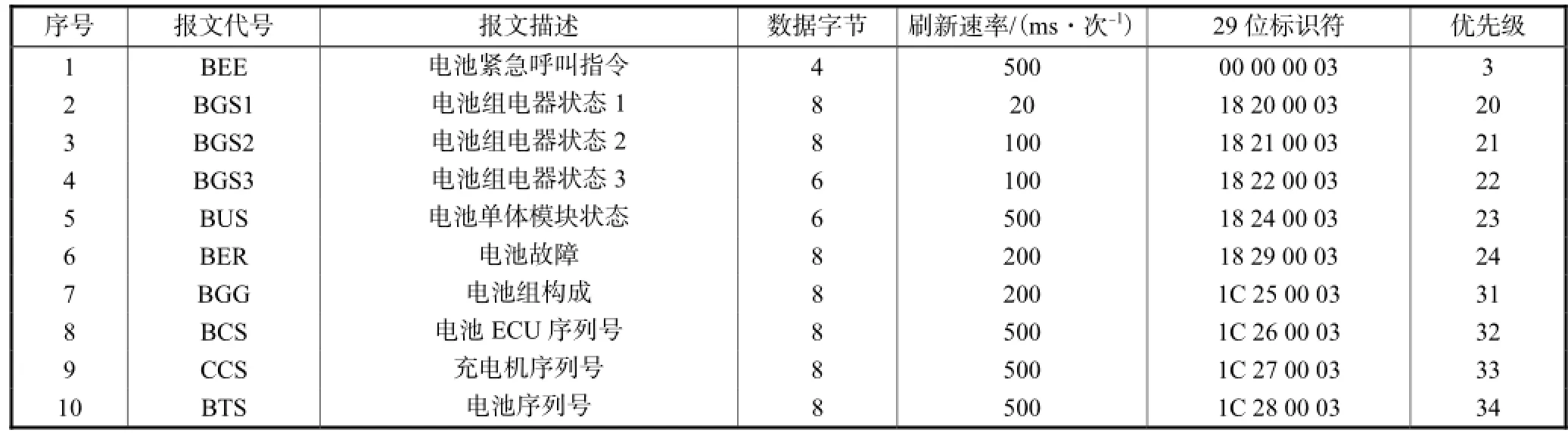
表6 电池ECU消息(节点号3，共10个消息)Tab.6 Messages of battery ECU(Node3，10 messages)

表7 整车故障消息(节点号6，共3个消息)Tab.7 Messages of fault(Node 6，3 messages)

表8 消息的传输时间、等待时间和响应时间的均值及最糟糕响应时间(共40个消息)Tab.8 Mean value and worst case values of transmission time，queuing time and response time(40 messages)

图10 基于网络负载率的消息响应时间均值分析Fig.10 Analysis of mean value of response time based on bus load

5 结 语

采用非强占优先级的M/G/1排队论模型研究了CAN总线消息响应时间均值的计算方法．针对CAN总线独有的填充位机制，采用数值模拟的方法得到了消息传输时间的概率分布．将上述方法用于电动汽车CAN总线消息响应时间均值的计算，分析了响应时间均值与总线负载率之间的关系，结果表明在负载率不大于35.92%的情况下，消息响应时间的均值与总线负载率近似成线性变化．

在利用排队论模型研究CAN总线响应时间均值的过程中，为简化计算，把离散概率分布的消息传输时间用连续概率分布来近似描述，这必然会带来一定的建模误差，今后拟采用离散时间排队理论对此问题进行更为深入的研究．

［1］ Davis R I Burns A，Bril R J，et al. Controller area network(CAN)schedulability analysis：Refuted，revisited and revised[J]. Real-Time Systems，2007，35(3)：239-272.

［2］ Tindell K，Burns A. Guaranteeing message latencies on controller area network[C]// Proceedings of 1st International CAN Conference．Wiesbaden，Germany，1994： 2-11.

［3］ Tindell K，Burns A，Wellings A J. An extendible approach for analysing fixed priority hard realtime systems[J]. Journal of Real-Time Systems，1994，6(2)：133-152.

［4］ Burns A. Preemptive priority based scheduling：An appropriate engineering approach[J]. Advances in Real-Time Systems，1994：222-245.

［5］ Giambene G．Queuing Theory and Telecommunications：Networks and Applications[M]. New York，USA：Springer，2005.

［6］ Nolte T，Hansson H，Norstom C. Using bit-stuffing distributions in CAN analysis[C]//IEEE Real-Time Embedded Systems Workshop. London，UK，2001：256-262.

［7］ Nolte T，Hansson H，Norstom C. Probabilistic worstcase response time analysis for the controller area network[C]// Proceedings of Real-Time and Embedded Technology and Applications Symposium. Toronto，Canada，2003：200-207.

［8］ International Organization for Standardization. 11898-1 Road Vehicles-Controller Area Network(CAN)-Part 1：Data Link Layer and Physical Signalling[S]. 2003.

［9］ Cobham A．Priority assignment in waiting line problems[J]. Operation Research，1954，2(1)：70-76.

［10］ 唐应辉，唐小我. 排队论基础与分析技术[M]. 北京：科学出版社，2006．

Tang Yinghui，Tang Xiaowo. Introductory and Analysis to the Queueing Theory[M]. Beijing：Science Press，2006(in Chinese).

［11］ Narayan B U. An Introduction to Queueing Theory：Modeling and Analysis in Applications[M]．Boston，USA：Birkhauser，2007.

［12］ CiA Draft Standard 102．CAN Physical Layer for Industrial Applications[EB/OL]. http：//www．can-cia．Org，2008-04-10．

Modeling and Analysis of Response Time of CAN Bus Based on Queueing Theory

CHEN Xi1，LIU Lu-yuan1，LÜ Wei-jie1，LI Fang2
(1. School of Electrical Engineering and Automation，Tianjin University，Tianjin 300072，China；2. Institude of Electrical Engineering，Chinese Academy of Sciences，Beijing 100190，China)

Response time of message of CAN is used to evaluate the real-time performance of CAN bus. Compared with the worst case response time analysis which focuses on the response time under extreme condition, analysis and modeling of mean value of response time were presented. According to the CSMA/CD protocol of CAN bus, a nonpreemptive priority M/G/1 model was introduced. Because bit-stuffing was adopted in CAN bus, the probability distribution function was calculated. Accordingly the mean value of response time was educed and the presented method was applied to a message dataset of electric vehicle. Results show that the mean value of response time is far less than the worst case response time. The above conclusions model the CAN bus based on queueing theory, which is available for the calculation of response time and theoretically helps the design and optimization of CAN based network system．

CAN bus；response time；queueing theory；priority；bit-stuffing

TP393.1

A

0493-2137(2012)03-0228-08

2010-10-11；

2011-03-15.

陈 曦（1980— ），男，博士研究生，讲师，chenxi@tju.edu.cn.

刘鲁源，liuly@tju.edu.cn.