斜坡上非均匀沙分组起动流速
吴 岩,韩其为,白玉川,
斜坡上非均匀沙分组起动流速
吴 岩1,韩其为1,白玉川1,2
(1. 天津大学河流海岸工程泥沙研究所,天津 300072;2. 天津大学水利工程仿真与安全国家重点实验室,天津 300072)
在经典力学的基础上,以某一概率为定量标准,根据斜坡上泥沙的受力状态,采用滚动模式进行理论推导,考虑了作用流速和颗粒位置的随机性、非均匀沙不同粒径之间的相互作用及不同倾角的影响,推导了斜坡上非均匀沙分组起动流速公式,通过实测资料验证表明,计算值与实测值符合较好.
斜坡;非均匀沙;暴露度;起动概率
泥沙起动在泥沙运动理论中是最基本的问题之一,在工程应用中,水库排沙、河床演变、航道治理以及桥梁冲刷、水环境保护等方面与泥沙起动均有密切的联系.在物理模型试验、数学模型计算中,起动流速又是必要的参数,因此泥沙起动规律及起动流速的研究在理论和实际应用方面均具有很重要的意义.
天然河流中的泥沙大多都是非均匀沙,即其粒径的尺寸是有一定范围的,是不同粒径的混合沙.对非均匀沙起动,国内外不少学者曾对此进行了研究,钱宁等[1]考虑床沙粗化过程来研究非均匀沙的起动问题;秦荣昱等[2]根据泥沙受力,推导了起动流速和最大起动粒径计算公式;孙志林等[3]对起动颗粒的作用力臂进行随机分析,导出考虑非均匀沙隐暴效应的起动概率表达式,建立非均匀沙第k粒级的起动公式.
冷魁等[4]与刘兴年等[5]在非均匀床沙暴露度的基础上,对非均匀沙的起动规律进行了探讨,提出了非均匀沙起动流速的计算公式;韩其为等[6]认为由于工程泥沙问题冲刷和粗化的需要,研究非均匀沙中不同粒径的起动问题尤为重要,即分组泥沙起动问题.
以往多研究平坡上泥沙的起动,当河道比降大时忽略泥沙颗粒自重沿水流方向的分力,就会有一定的误差.对于斜坡上泥沙起动条件的研究至今较少.文献[7]从休止角的角度出发,研究了均匀沙的临界起动力的状况;陈奇伯等[8]利用水槽试验研究了三峡坝区非黏性均匀花岗石沙粒的起动流速情况,何文社等[9]从理论上推导了非均匀沙的临界起动剪切力,但其理论缺少试验资料的支持.笔者从暴露度(隐蔽度)的角度出发,建立了斜坡上非均匀沙的起动流速公式,更符合天然河流中的实际情况,理论计算值与试验值符合较好.
1 理论分析
1.1暴露度分析
目前非均匀沙起动规律研究中,表示泥沙之间的相互影响常采用附加作用力法[2]和暴露度法[9-11].笔者则沿用韩其为等[12]提出的相对暴露度概念,即任意一泥沙颗粒在床面的位置是随机的,可能被其他周围泥沙所掩盖而不能起动,即完全遮蔽;也可能位于前后泥沙的顶部,很容易起动,即完全暴露;一般情况的泥沙位置是介于这二者之间,如图1所示.可用研究颗粒最低点a至与其相邻的下游颗粒接触点b之间的竖直距离Δ来表征颗粒在床面的位置,Δ可简称为暴露度;Δ愈小,表示暴露愈充分.它较后来Paintal[13]提出的暴露度既简单又能在力学分析时引入有关公式中[14],而不只是一种校正系数.
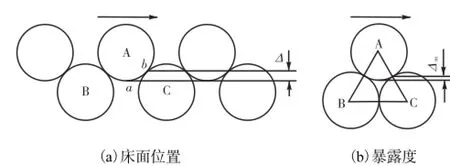
图1 颗粒在床面位置的暴露度示意Fig.1 Exposure degree diagram of particles in bed position
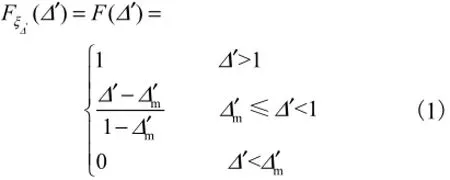
式中:Δξ′为Δ′的随机变量;mΔ′为Δ′的最小值,对于均匀颗粒,且紧密排列时,mΔ′=0.134,如图1所示.
式(1)还表明mΔ′<0.134及mΔ′>1是不可能的,因为前者表示没有光滑床面;后者则表示当Δ′=1时,颗粒已位于床面第2层,而没有暴露,故不可能起动.
Δ′的数学期望为
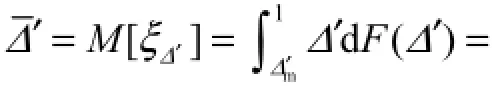
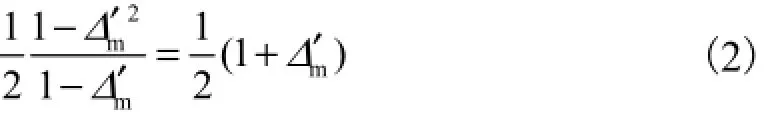
对于非均匀沙,一般按实测床沙级配资料,定义其概率函数为
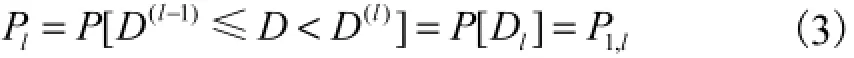
式中:1,lP为床沙级配,即第l组粒径的泥沙(D(l-1)≤D<D(l))所占质量分数;D为泥沙粒径;Dl为该组的平均粒径;D(l-1)及D(l)为其上、下界限粒径.上、下界限粒径的平均粒径为

式中n为粒径分组数、非均匀沙在床面位置的分布较为复杂[15-16].其相对暴露度仍定义为

将泥沙分为粗颗粒、中等颗粒和细颗粒,3种不同粒径的数学期望分别为

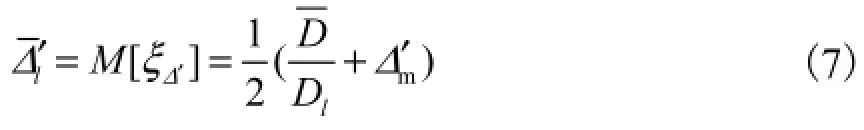
当Dl≤时为细颗粒,有

1.2斜坡泥沙起动公式的建立
从图2中可以看出,泥沙颗粒受力为

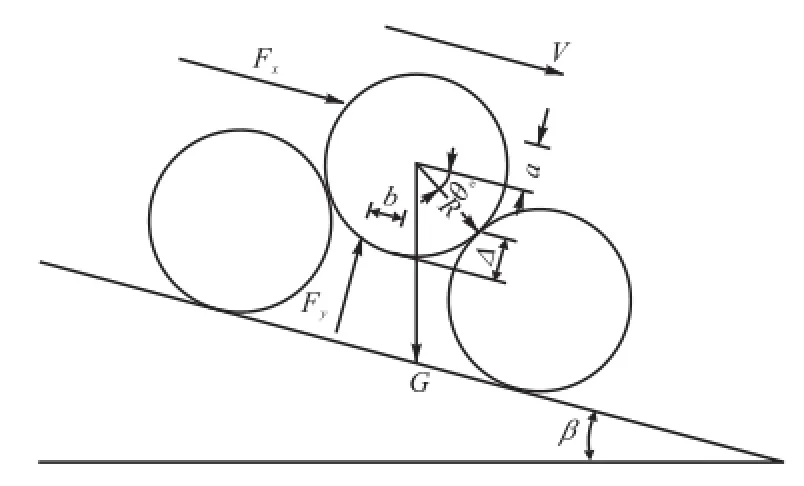
图2 颗粒在床面的位置以及受力Fig.2 Particles diagram in bed position and force

式中:Fx为正面推力;Fy为上举力;G为水下重力;Cx为正面推力系数,取为0.4;Cy为上举力系数,取为0.1[6];为起动的临界水流瞬时底速;ρs和ρ分别为泥沙及水的密度;D为泥沙粒径.
从图2中可得
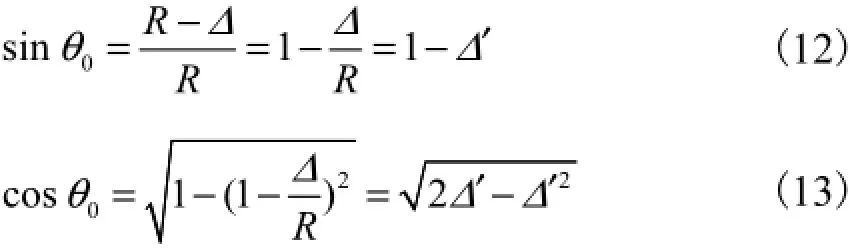
由图2的力矩平衡可得颗粒的起动概率为
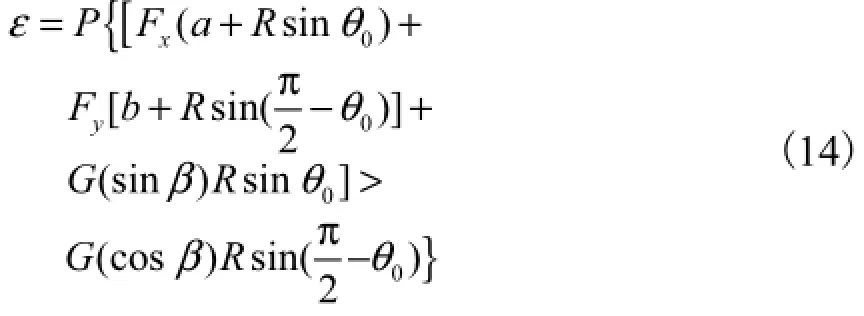
式中:参数a为正面推力到泥沙颗粒中心的垂直距离;参数b为上举力到泥沙颗粒中心的垂直距离;β为倾斜面与水平面的夹角.
将石油安全评价指标数据矩阵X=(xij)m×n各个数据带入到相应的白化权函数中,运用式(8)计算得出各指标的灰色统计数,见表7。然后,根据表7中的灰色统计数及式(9),可得出石油安全模糊评价权矩阵R。

令

即
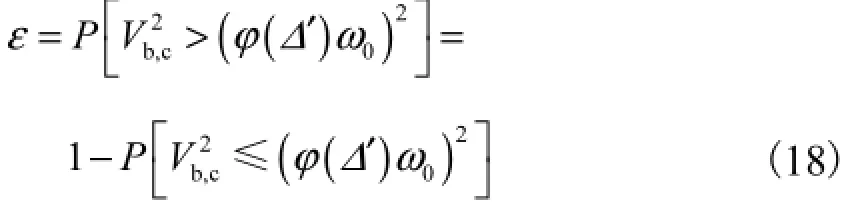
因为水流瞬时底速bV服从正态分布,其密度函数为

式中:Vb为瞬时纵向底速;为时均底速;σ为均方差.
因此,式(18)可表示为
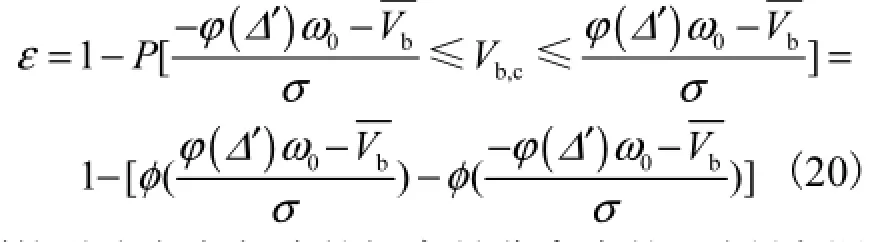
颗粒逆流方向起滚的概率是非常小的,对研究泥沙起动来说意义不大[6],一般忽略不计,故



均值满足对数公式由于是粗糙床面,故1x=.底层流速作用点的位置取床面粗糙度s2kd=[17],由此可得到

窦国仁[18]将泥沙的起动概率分为:弱动(个别泥沙颗粒起动)时,P=0.0014;中动(少量泥沙颗粒起动)时,P=0.0227;强动(大量泥沙颗粒起动)时,P=0.1585.本文以泥沙少量起动时起动概率作为起动标准,即P=0.0227.
垂线平均流速V与u∗之间有[6]
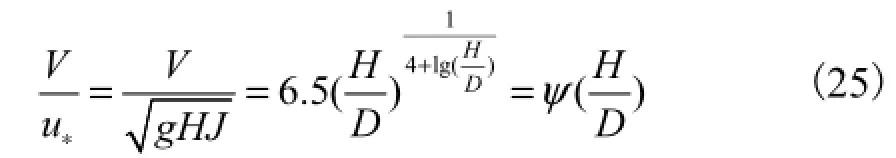
由式(25)可得水流垂线平均流速为
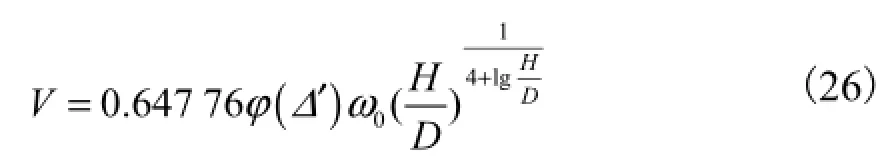
对于非均匀沙,仅需将式(26)中的D用lD代替,0ω用0,lω代替,l表示粒径组,而与Δ′相对应的有,其中,lR为l组泥沙的半径.
2 斜坡非均匀沙起动流速公式验证
采用文献[6]对式(26)进行了验证.
表1列出了本文中的起动流速公式与文献[6,19]起动流速公式以及试验的结果.
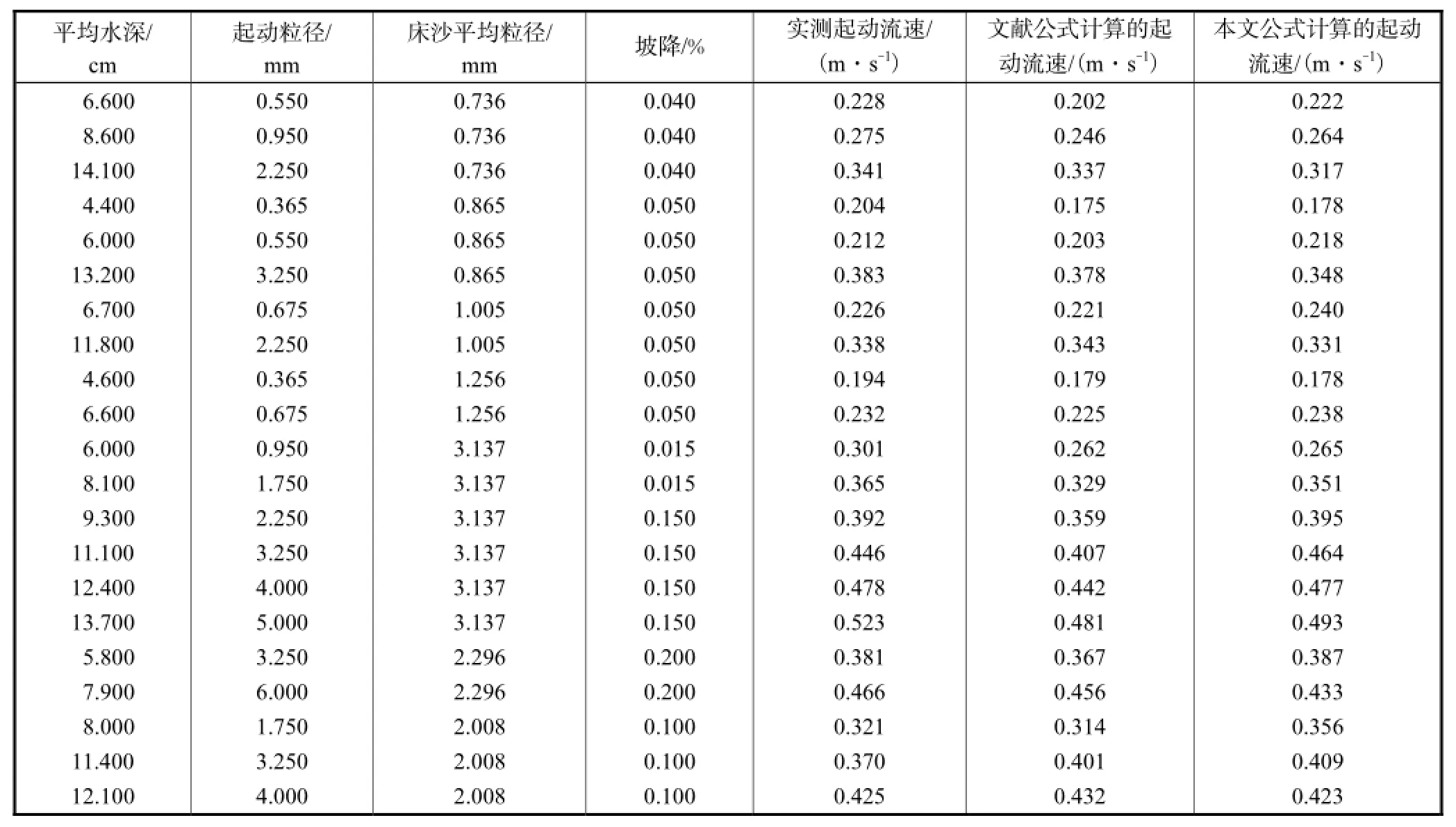
表1 较缓斜坡非均匀沙起动流速实测值与计算值比较Tab.1 Comparison between experimental and calculated non-uniform sediment incipient velocity on moderate slope
从表1和图3可以看出,在不同水深、比降以及泥沙粒径的条件下,本文的起动流速计算值与文献[6]的起动流速计算值以及试验实测起动流速值都很接近.通过计算可知,本文的计算起动流速值与实测的起动流速值的相关系数为0.977,说明本文的起动流速公式可以很好地预测坡度较缓情况下的泥沙起动流速.
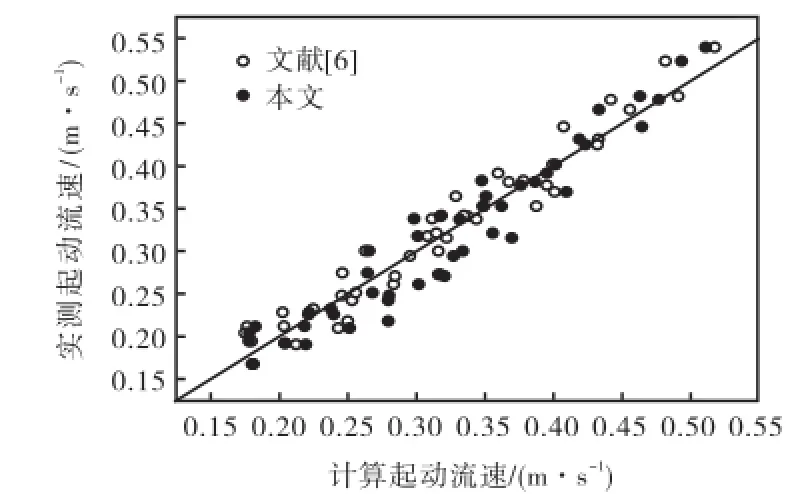
图3 泥沙起动流速计算值与试验值相关性Fig.3 Correlation of experimental and calculated sediment incipient velocity
陈奇伯等[8]用铁板制成长2.00,m、宽0.17,m的倾角可调式试验用槽.试验中选取的泥沙粒径D分别为1.5,mm、3.5,mm、7.5,mm.每种粒径试验了6种底坡,底坡θ分别为5ο、10ο、15ο、20ο、25ο、30ο,共18种组合进行了实测资料验证.因为其试验采用的是均匀沙,且取P=0.159作为判别泥沙起动的统一定量标准,作为非均匀沙起动的一种特殊情况,通常当河床组成为均匀沙时,取河床粗糙度Ks=D,由于陈奇伯与笔者采用的判别泥沙起动标准不一样,泥沙起动流速就不一样.为了便于使用他的试验数据验证,笔者也按他的起动标准即P=0.159来计算起动流速.其计算值与实测起动流速对比结果列于表2.
从表2的结果可以看到,计算结果与实测值比较符合.一般误差在-25%~6%之间,说明将暴露度引入到斜坡泥沙起动流速中,并考虑重力沿水流方向的分力是合理的,同一粒径泥沙颗粒起动流速随着斜坡倾角β的增大而减小,在同一坡度上,粒径大的颗粒较粒径小的颗粒起动流速大.在泥沙粒径为1~2,mm时,起动流速计算值比试验值偏大,但若采用推导公式时用的“个别起动”标准,计算值与实测值颇为接近.除此之外,造成起动流速计算值比试验值偏大这一结果,与床面泥沙上举力系数的确定也是有一定关系的.本文中直接取LC为0.1,文献[20]通过试验发现粒径为0.14~2.0,mm的泥沙,上举力系数LC至少大于0.25,根据本文的公式推导过程,可知随着上举力系数CL的增大,式(26)中的φ(Δ′)值减小,水流垂线平均流速减小.不同的泥沙粒径在坡度β=30ο时较其他坡度时的误差大,除了由于实测资料有一定波动外,是否存在一个临界坡度,在临界坡度内,此公式更加适合,是有待进一步研究的问题.
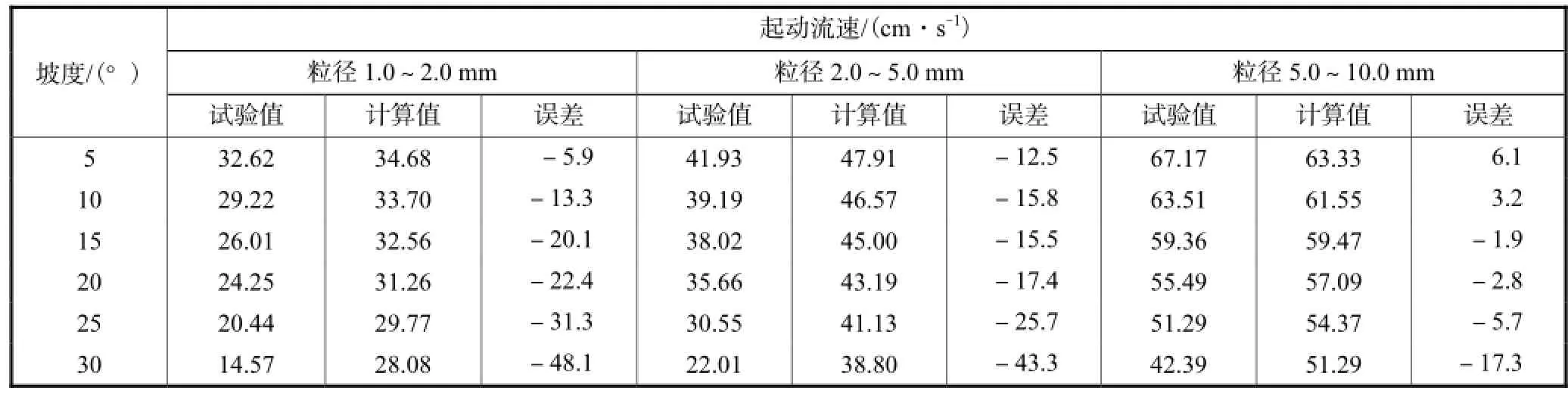
表2 一定坡度泥沙起动流速试验值与计算值的比较Tab.2 Comparison between experimental and calculated sediment incipient velocity on certain slope
3 结 语
将颗粒在床面的位置参数相对暴露度Δ′引入起动流速公式中,并考虑了斜坡坡度的影响,非均匀沙的起动流速随斜坡倾角β的增大而减小,β对起动临界条件的影响较明显,可见在河流和渠道的比降大时,考虑自重沿水流方向的分力是极其重要的.
采用实测资料对文中斜坡上非均匀沙起动流速公式进行了验证,吻合较好.
[1] 钱 宁,万兆惠. 泥沙运动力学[M]. 北京:科学出版社,1983.
Qian Ning,Wan Zhaohui. Mechanics of Sediment Transport[M]. Beijing:Science Press,1983(in Chinese).
[2] 秦荣昱,王崇浩. 河流推移质运动理论及应用[M].北京:中国铁道出版社,1996.
Qin Rongyu,Wang Chonghao. Theory and Application of Bed Load Movement in River[M]. Beijing:China Railway Press,1996(in Chinese).
[3] 孙志林,谢鉴衡,段文忠,等. 非均匀沙分级起动规律研究[J]. 水利学报,1997(10):25-32.
Sun Zhilin,Xie Jianheng,Duan Wenzhong. Incipient motion of individual fractions of nonuniform sediment[J]. Journal of Hydraulic Engineering,1997 (10):25-32(in Chinese).
[4] 冷 魁,王明甫. 无黏性非均匀沙起动规律探讨[J].水力发电学报,1994,45(2):57-65.
Leng Kui,Wang Mingfu. The law of non-cohesive and non-uniform sediment[J]. Journal of Hydroelectric Engineering,1994,45(2):57-65(in Chinese).
[5] 刘兴年,曹叔尤. 粗细化过程中的非均匀沙起动流速[J]. 泥沙研究,2000,8(4):10-13.
Liu Xingnian,Cao Shuyou. Critical velocity of nonuniform sediment in the armoring process[J]. Journal of Sediment Research,2000,8(4):10-13(in Chinese).
[6] 韩其为,何明民. 泥沙起动规律及起动流速[M]. 北京:科学出版社,1999.
Han Qiwei. He Mingmin. The Incipient Disciplinarian and Incipient Velocity of Sediment[M]. Beijing:Science Press,1999(in Chinese).
[7] Chiew Y M,Parker G. Incipient sediment entransport on non-horizontal slopes[J]. Journal of Hydraulic Research,1994,32(5):649-660.
[8] 陈奇伯,解明曙,张洪江. 三峡坝区非黏性均匀花岗岩砂粒起动条件研究[J]. 人民长江,1996,27(7):13-14.
Chen Qibo,Xie Mingshu,Zhang Hongjiang. Incipient motion conditions of non-cohesive uniform granite grains in Three Gorges dam region[J]. Yangtze River,1996,27(7):13-14(in Chinese).
[9] 何文社,曹叔尤,袁 杰,等. 斜坡上非均匀沙起动条件初探[J]. 水力发电学报,2004,23(4):78-81.
He Wenshe,Cao Shuyou,Yuan Jie,et al. Incipient motion of non-uniform sediment particles on sloping fluvial beds[J]. Journal of Hydroelectric Engineering,2004,23(4):78-81(in Chinese).
[10] 刘兴年. 非均匀沙推移质输沙率及其粗化稳定[D]. 成都:四川大学水利水电学院,1986.
Liu Xingnian. Non-Uniform Sediment Bed Load Transport Rate and Coarsening and Stability[D]. Chengdu:College of Water Resource and Hydropower,Sichuan University,1986(in Chinese).
[11] 何文社,杨具瑞. 泥沙颗粒暴露度与等效粒径研究[J]. 水利学报,2002,33(11):44-48.
He Wenshe,Yang Jurui. Relative exposure degree and equivalent grain size of non-uniform sediment[J]. Journal of Hydraulic Engineering,2002,33(11):44-48(in Chinese).
[12] 韩其为,何明民. 泥沙运动统计理论[M]. 北京:科学出版社,1984.
Han Qiwei,He Mingmin. Statistics Theory of Sediment Motion [M]. Beijing:Science Press,1984(in Chinese).
[13] Paintal A S. A stochastic model of bed load transport[J]. J Hyd Res,1971,19(4):527-554.
[14] 何明民,韩其为. 单颗粒泥沙运动力学及统计规律[J]. 力学与实践,1971,1(4):35-37.
He Mingmin,Han Qiwei. The mechanics and statistical laws of single sediment movement[J]. Mechanics in Engineering,1971,1(4):35-37(in Chinese).
[15] 韩其为.泥沙起动规律及起动流速[J]. 泥沙研究,1982(2):11-26.
Han Qiwei.Characteristics of incipient sediment motion and incipient velocity[J]. Journal of Sediment Research,1982(2):11-26(in Chinese).
[16] 韩其为,何明民. 非均匀沙起动机理及起动流速[J].长江科学院院报,1996,3(13):12-17.
Han Qiwei,He Mingmin. Incipient mechanism and incipient velocity of nonuniform sediment[J]. Journal of Yangtze River Scientific Research Institute,1996,3(13):12-17(in Chinese).
[17] Cheng Niansheng,Yee-Meng Chiew. Pickup probability for sediment entrainment[J]. Journal of Hydraulic Engineering,ASCE,1998,124(2):232-235.
[18] 窦国仁. 再论泥沙起动流速[J]. 泥沙研究,1999 (6):1-9.
Dou Guoren. Incipient motion of coarse and fine sediment[J]. Journal of Sediment Research,1999(6):1-9(in Chinese).
[19] 马 菲,韩其为,李大鸣. 非均匀沙分组起动流速[J]. 天津大学学报,2010,43(11):977-980.
Ma Fei,Han Qiwei,Li Daming. Incipient velocity of individual fractions of non-uniform sediment[J]. Journal of Tianjin University,2010,43(11):977-980(in Chinese).
[20] 李昌华,孙梅秀. 床面上泥沙绕流上举力系数的间接确定[J]. 泥沙研究,1984(4):60-63.
Li Changhua,Sun Meixiu. The indirect determination of lift coefficient of flow around the surface of sediment on the bed[J]. Journal of Sediment Research,1984(4):60-63(in Chinese).
Incipient Velocity of Non-Uniform Sediment on Sloping Fluvial Beds
WU Yan1,HAN Qi-wei1,BAI Yu-chuan1,2
(1. Institute of Sediment on River and Coast Engineering,Tianjin University,Tianjin 300072,China;2. State Key Laboratory of Hydraulic Simulation and Safety,Tianjin University,Tianjin 300072,China)
Based on the method of classical mechanics theory combined with a probability as quantitative criteria and according to the sediment stress states on different slopes, a rolling model was adopted to conduct a theoretic deduction. The flow velocity and the random position of non-uniform sediment on the sloping bed, the interaction between different particle sizes and the influence of different angles were taken into account; then the formula for calculating the incipient velocity of non-cohesive and non-uniform sediment on sloping bed was established. The validity of the formula is verified by experimental data.
sloping bed;non-uniform sediment;degree of exposure;probability of starting
TV142
A
0493-2137(2012)03-0209-06
2011-06-29;
2011-10-14.
国家重点基础研究发展计划(973计划)资助项目(2007CB714101);国家自然科学基金资助项目(50809045,51009105);教育部博士点基金资助项目(200800561098).
吴 岩(1985— ),女,博士研究生,wuyan@tju.edu.cn.
白玉川,ychbai@tju.edu.cn.

