基于自适应卡尔曼滤波的GNSS矢量锁定环路

赵思浩，陆明泉，冯振明

(清华大学电子工程系，100084 北京)

基于自适应卡尔曼滤波的GNSS矢量锁定环路

赵思浩，陆明泉，冯振明

(清华大学电子工程系，100084 北京)

为了减小卫星信号信噪比变化对全球导航卫星系统(GNSS)接收机当中矢量锁定环路(VLL)的不良影响，使用一种基于新息的自适应卡尔曼滤波方法对其改进，以实现对VLL滤波器观测噪声协方差矩阵的实时调整.使用后处理软件全球定位系统(GPS)接收机处理信号发生器产生的中频数据以对提出的方法进行验证.实验结果表明，相对于传统标量环路(SLL)，基于自适应卡尔曼滤波的VLL可以在信噪比降低甚至可见卫星数目不足的环境下工作，其载波频率跟踪精度及导航定位解精度均优于固定参数矢量环路和传统标量环路.

全球导航卫星系统;矢量锁定环路;自适应卡尔曼滤波

经过30余年的发展，以全球定位系统(GPS)为代表的全球导航卫星系统(GNSS)已经得到了非常广泛的应用.目前，GPS接收机对于导航信号的处理流程一般包括卫星信号捕获、载波/伪随机码跟踪、导航数据解调以及定位解算等步骤.其中，载波/码跟踪是一个非常重要的环节，如果对信号的跟踪失败，后续步骤将无法进行.例如在GPS信号受到干扰、遮挡或者接收机进行高动态运动的情况下，传统的标量跟踪环路(SLL)将无法对信号进行有效地跟踪，最终导致定位失败.利用各通道之间的相关性，就可以使用信号较强通道的跟踪结果辅助信号较弱的通道，从而使接收机的性能得到提高，这种各个通道之间互相辅助的思想被称为矢量跟踪.矢量跟踪环路的概念由Spilker［1］首 先 提 出，Petovello［2－3］，Lashley［4］，Zhao［5］等人的研究表明，矢量环路在跟踪各个通道信号的同时可以完成对接收机位置和速度的解算，相对于标量环路，矢量环路可以在更低的信噪比条件下正常工作.

在之前的研究中，有学者将卡尔曼滤波器应用于矢量环路或者类似的功能当中，但多数并没有讨论参数的设定方法或者仅仅是手动设定滤波参数［4－7］.而过程噪声和测量噪声的设置直接影响了卡尔曼滤波器的性能，由于工作环境的变化，固定的参数设置由于无法及时反映环境变化很可能带来性能的下降.本文在以上工作基础上使用一款 Matlab软件接收机作为平台［8］，进一步将Mohamed等人提出的基于新息的自适应卡尔曼滤波算法引入了该矢量环路［9］，使其具有实时设定观测噪声协方差矩阵的能力.使用GPS信号发生器产生的中频数据进行测试，对基于该自适应滤波算法的矢量环路的性能进行了评估.

1 矢量环路工作原理

SLL使用锁频环(FLL)、锁相环(PLL)和延迟锁定环(DLL)同时跟踪来自不同卫星的信号，各个通道间彼此独立地提供伪距、伪距率测量结果.由于各个通道间没有信息的共享，因此某一通道出现的异常不会影响其他通道的跟踪性能.需要注意的是，各个通道接收的信号实际上是通过唯一的接收机位置和速度联系在一起的，因此，可以利用这一特性为各个通道的伪距、伪距率等观测量建立联系.

以GPS接收机为例，根据其工作原理，需要至少4颗可见卫星信号提供的伪距、伪距率测量值才能得到接收机的位置、速度、时钟偏差和时钟漂移［10］.跟踪环路当中的伪距、伪距率来源于伪随机码相位和载波多普勒测量值，如果已知用户位置和卫星位置，则可以求解伪随机码相位.矢量环路正是基于这个思想.

如图1所示，在某一时刻k，对接收机位置进行估计，估计值记为 ^Xk，接收机真实位置记为Xk，则对应的码相位误差可以写为

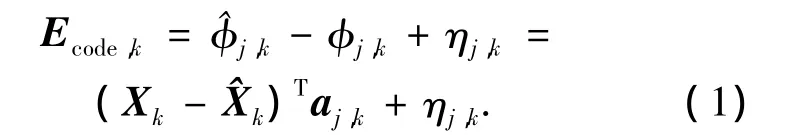
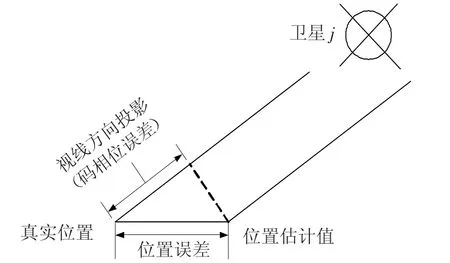
图1 位置误差与码相位误差的关系

式中:^φj，k为k时刻对第j颗卫星信号码相位的估计值，φj，k为码相位真实值，aj，k为由用户指向第 j颗卫星的视线方向单位向量，ηj，k为未模型化的误差项.如果考虑到接收机本地时钟的偏差，可以将(1)改写为

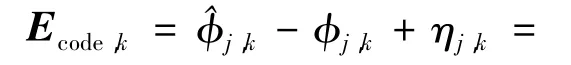
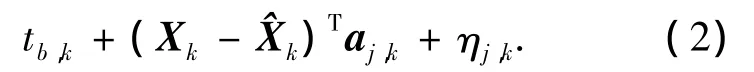
同理，载波频率误差与速度误差的关系可以写为

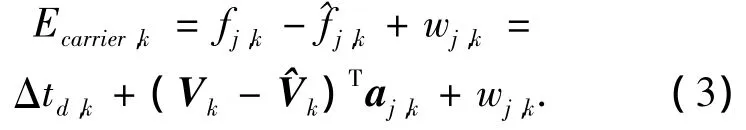
式(2)和式(3)可以作为卡尔曼滤波器当中的测量方程，码相位误差和载波频率误差测量值可以通过码相位鉴别器和载波频率鉴别器得到.

如果我们选取接收机3个方向的位置误差、3个方向的速度误差以及时钟偏差和时钟漂移误差作为状态量［5］，那么过程方程可以写为:

式中:Fk，k+1为离散化的一步状态转移矩阵，Wk为过程噪声.

在Matlab的软件接收机中实现矢量环路的流程如图2所示.

矢量环路需要接收机位置、速度、各个通道的码相位、码频率、载波相位和时钟误差作为初始值，然后对下一时刻的以上各个参量进行估计，利用该估计值在视线方向上的投影产生本地复现的伪随机码和载波，经过积分/清零运算，利用码相位误差鉴别器和载波频率误差鉴别器得到各个通道信号含有噪声的码相位误差和载波频率误差，输入到卡尔曼滤波器当中，得到该时刻各个参量的估计值与真实值的误差，修正估计值后输出，然后进入下一次滤波过程.

2 基于新息的自适应卡尔曼滤波算法

在矢量环路当中，使用了卡尔曼滤波器对状态量进行估计.为了获得更好的跟踪和导航精度，有必要对滤波参数的设置进行探讨.我们将系统离散化的过程方程和测量方程重写如下:

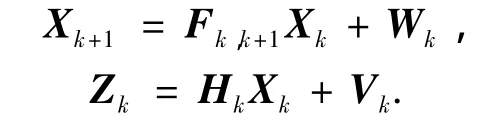
式中:Xk+1为k+1时刻系统的状态，Fk，k+1为离散化的一步状态转移矩阵，Zk为k时刻观测量，根据文献［10］，Zk当中包含了各个通道码相位误差鉴别器以及载波频率误差鉴别器的输出值，Hk为观测矩阵.

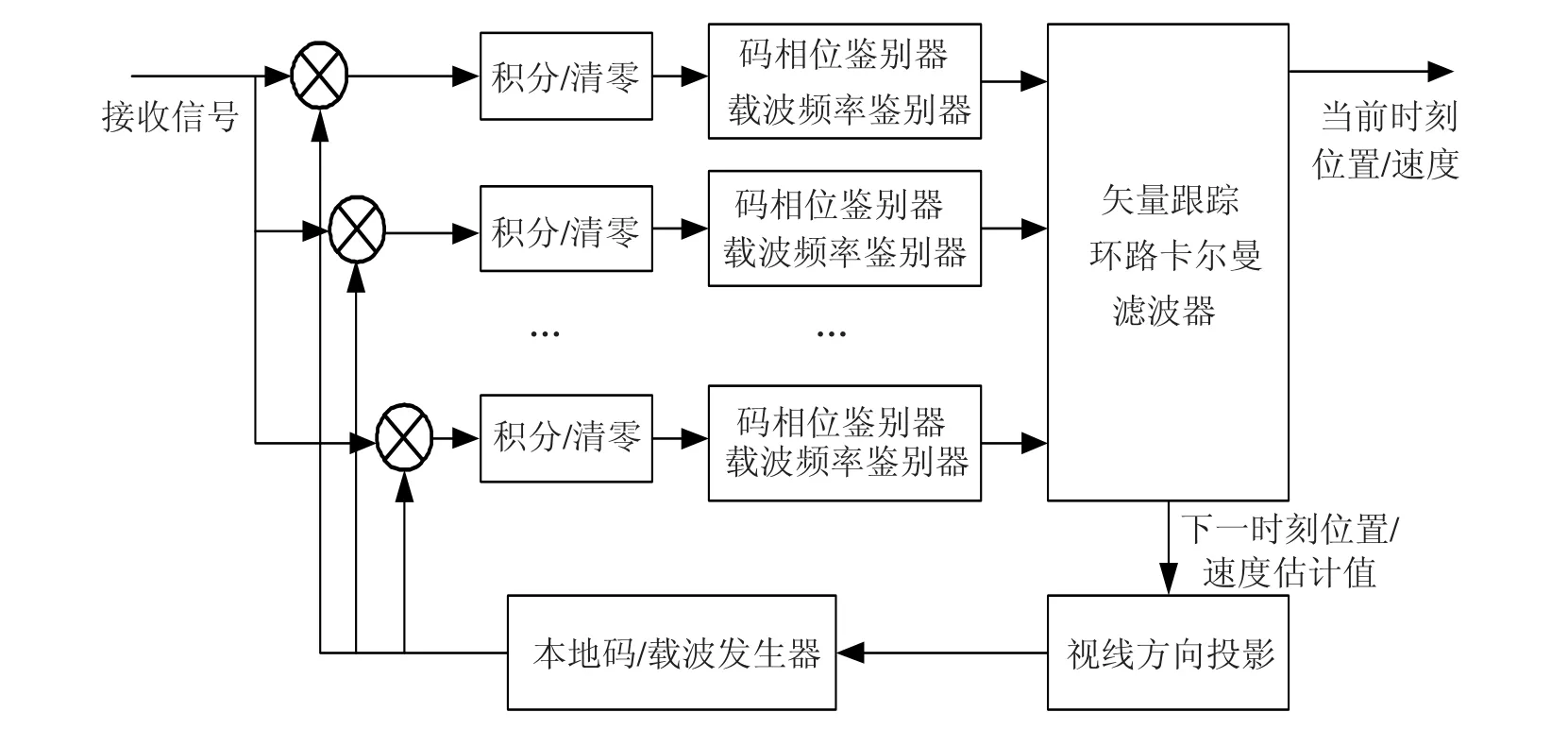
图2 矢量环路工作流程

将过程噪声Wk的协方差矩阵记为Qk，测量噪声Vk的协方差矩阵记为Rk.根据上文给出的矢量环路工作原理和式(4)，可以看出，Qk当中包含的是接收机位置、速度以及时钟误差相关的噪声项，这些项可以通过接收机运动状态，本地时钟的等级等先验知识进行比较准确的设定，在实际的应用过程当中这些值一般可以满足性能要求，因此只需要设定一个固定值即可.根据式(2)和式(3)，测量噪声协方差矩阵Rk当中包含了接收机当中各个通道的码相位误差以及载波频率误差噪声项，假设各个通道码相位误差和载波频率误差之间不相关，则Rk为对角阵，其对角线元素都是与实际接收到信号的信噪比有关，当卫星信号受到干扰或遮挡时，实际的噪声项会发生较大的变化，如果仅仅使用固定的值，很可能无法反应接收信号的变化情况，因此需要考虑使用一种实时设定矩阵Rk的方法.

为了方便下面的讨论，将卡尔曼滤波基本方程重写如下［11］.

估计误差方差:

卡尔曼增益:

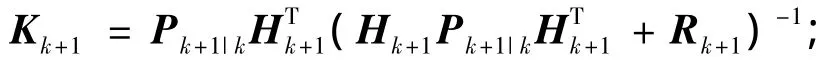
状态估计:

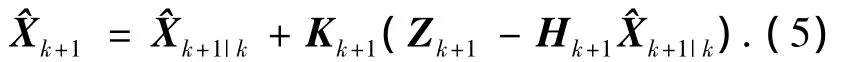
式(5)中(Zk+1-Hk+1^Xk+1|k)被称为新息.理想状态下稳态滤波器的新息应为零均值白噪声序列，自适应滤波的思想是使卡尔曼滤波的新息或残差与它们理论上的协方差相匹配.为了使用新息序列来估计测量噪声协方差矩阵Rk，文献［9］给出了一种使用最大似然准则进行估计的方法:

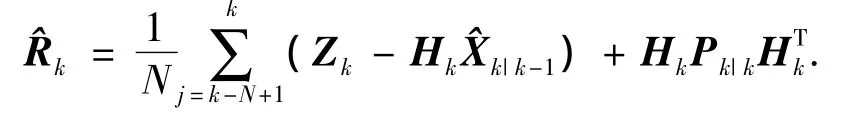
式中:N为连续截取的新息数量，为了保证估计的结果是无偏的，N的选取越大越好，但是考虑到实际接收信号信噪比的变化，如果将N值取的过大则无法及时反映这种变化，因此需要根据应用的场景进行折中考虑.

3 实验及结果

使用GPS信号发生器产生的225 s中频数据，该段数据中，车载GPS接收机在水平面内进行8字型运动，运动速度为50 m/s.整个过程中，初始的50 s内共有10颗卫星可见，之后的175 s内，有的卫星时而被遮挡，时而重新可见，这是信号信噪比变化的极端情况，在城市和峡谷当中比较常见.总的可见卫星数目随时间的变化如图3所示.可见，在58 s左右，可见卫星数目会下降到小于4颗，在之后的时间内，可见卫星数也经常低于4颗，传统标量环路可能受到影响甚至无法工作.

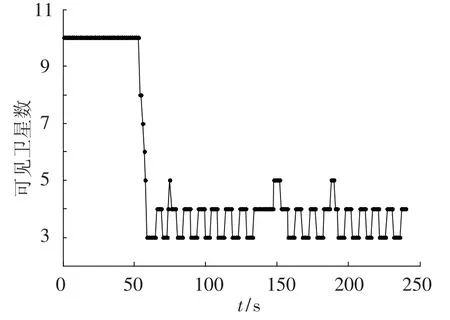
图3 可见卫星数目随时间的变化

在数据开始的45 s内使用标量环路处理数据，然后切换到矢量环路处理余下的180 s数据.分别测试了使用自适应方法设定测量噪声协方差矩阵的矢量环路和使用固定测量噪声协方差矩阵的矢量环路.两种矢量环路均使用1 ms接收数据进行积分与清零运算.自适应方法当中选取连续的500 ms数据(即连续500个观测量)计算R矩阵中的对应项，参数设定如表1所示.作为比较，同时也使用标量环路对该段数据进行了处理，参数设置如表2所示.矢量环路具有与传统标量环路相同的预检测积分时间.

表1 两种矢量环路的参数设置

表2 标量环路参数设置

由图4所示是其中PRN19和PRN14号卫星的载波频率跟踪结果(图中标量环路记为SLL，固定参数的矢量环路记为VLL，自适应矢量环路记为Adaptive VLL，下同)，其他通道卫星信号的频率跟踪结果类似.图4中的柱状图是3种方法得到的频率误差统计结果，从实验当中采样点数量来看，自适应矢量环路的频率跟踪结果更多的集中在误差更小的区间内，而标量环路的结果在误差较大的区间内仍有较多的采样点.可以看到，矢量环路由于各个通道之间共享信息而得到了比标量环路更准确的频率跟踪结果，而使用自适应方法的矢量环路得到的频率跟踪结果误差更小.

由图5、图6展示了接收机位置和速度结果，同样使用了柱状图统计了不同位置误差和速度误差区间当中几种方法获得的结果样本点数.使用标量环路的接收机在处理时间大于58 s时由于可见卫星数目频繁且长时间小于4颗而很快无法准确给出定位结果，而矢量环路则可以保持正常工作，三者当中，使用自适应方法的矢量环路性能最优，给出的三维位置结果误差不超过220 m，给出的三维速度结果误差不超过30 m/s.

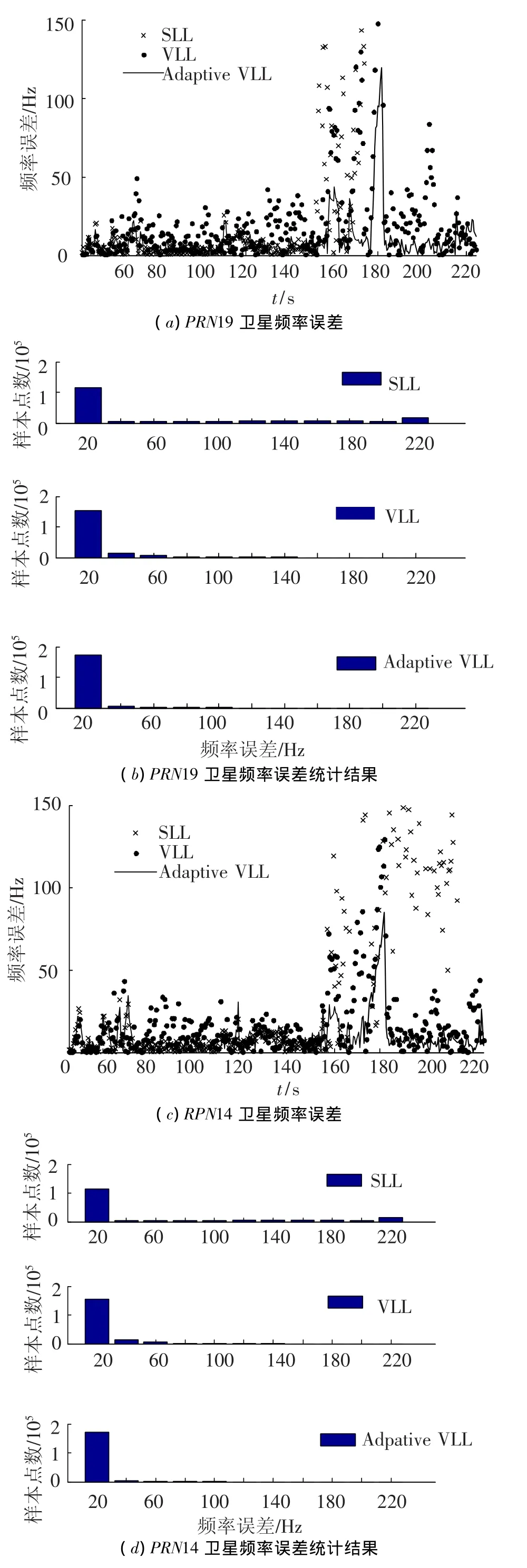
图4 频率跟踪误差

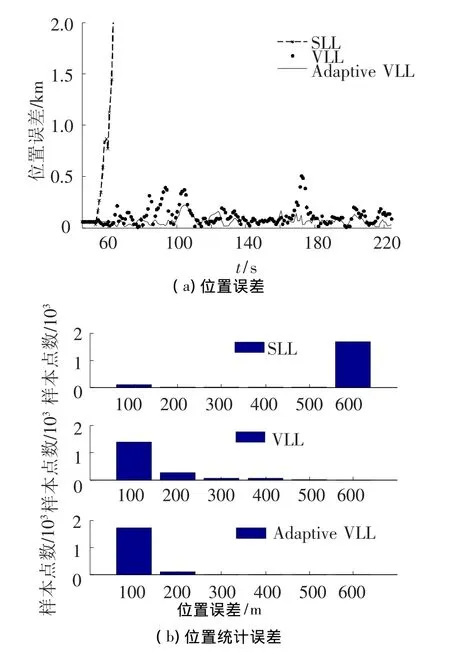
图5 位置误差

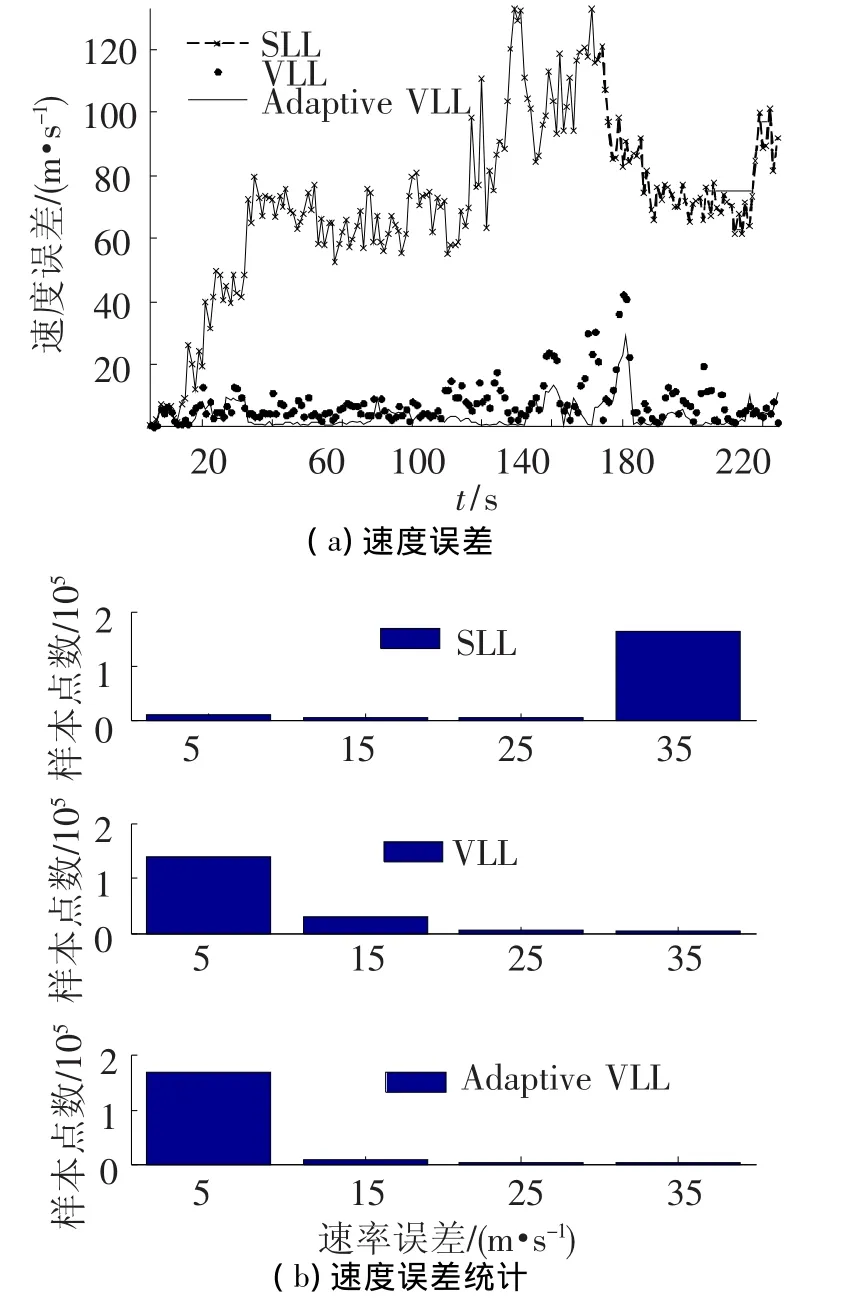
图6 速度误差

4 结论

在低信噪比及卫星信号受到遮挡的情况下，传统的标量环路无法正常工作，更无法给出定位结果;矢量环路能够保持工作，但性能下降.针对这一问题，本文提出了一种应用于GNSS接收机矢量环路中的自适应滤波方法，该方法对观测噪声协方差矩阵进行实时设定，以减小信号恶化通道的观测量产生的不良影响，从而提升GNSS接收机性能.使用一组在信号受到遮挡情况下的GPS仿真数据进行实验，结果表明，本文提出自适应矢量环路可以在卫星信号受到遮挡导致可见星数目小于4的环境下正常工作，给出与真实值匹配较好的载波频率跟踪结果以及位置速度结果.相对于传统标量环路以及使用固定测量噪声协方差矩阵的矢量环路，使用自适应滤波方法可以提供更高的载波频率跟踪精度及位置和速度精度.

［1］PARKINSON B W，SPILKER J J.Global Positioning System:Theory and Apolications［M］.Washington，DC:American Institute of Aeronautics and Astronautics，1996:245－325.

［2］PETOVELLO M G，Lashley M，Bevly D M.What about vector tracking loops［J］.Inside GNSS，2009，(3):6 －11.

［3］PETOVELLO M G，Lachapellle G.Comparison of vector-based software receiver implementations with application to ultra-tight GPS/INS integration［C］//Proceedings of ION GNSS 2006，Forth Worth，TX:Institute of Navigation，2006:1790－1799.

［4］LASHLEY M.Modeling and performance analysis of GPS vector tracking algorithms［D］.Auburn，USA:Auburn University，2009:65 －85.

［5］ZHAO Shi-hao，AKOS D.An open source GPS/GNSS vector tracking loop—implementation，filter tuning，and results［C］//Proceedings of ION ITM 2011，San Diego，CA:Institute of Navigation，2011:1293 －1305.

［6］BHATTACHARYYA S，GEBRE-EGZIABHER D.Development and validation of a parametric model for vector tracking loops［C］.//Proceedings of ION GNSS 2009，Savannah，GA:ION，2009:186－200.

［7］CRANE R.A simplified method for deep coupling of GPS and inertial data［C］.//Proceedings of ON NTM 2007，San Diego，CA:Institute of Navigation，2007:311－319

［8］BORRE K，AKOS D.A Software-Defined GPS and Galileo Receiver:A Single-Frequency Approach［M］.New York:Springer，2007:143 －150.

［9］MOHAMED A H，SCHWARZ K P.Adaptive kalman filtering for INS/GPS［J］.Journal of Geodesy，1999，73:193－203.

［10］KAPLAN E D，HEGARTY C J.Understanding GPS Principles and Applications.Norwood ［M］，MA，USA:Artech House，Inc.，2006:50 －57.

［11］秦永元，张洪钺，汪叔华.卡尔曼滤波与组合导航原理［M］.西安:西北工业大学出版社，1998:34－35.

GNSS vector lock loop based on adaptive Kalman filter

ZHAO Si-hao，LU Ming-quan，FENG Zhen-ming
(Dept.of Electronic Engineering，Tsinghua University，100084 Beijing，China)

To mitigate the negative impact of varying satellite signal-to-noise ratio(SNR)on the vector lock loop(VLL)in a Global Navigation Satellite System(GNSS)receiver，an innovation based adaptive Kalman filter is employed to real-time adjust VLL measurement noise covariance matrix.Intermediate frequency data from a Global Positioning System(GPS)signal generator are post-processed using a software GPS receiver to verify the proposed method.The experimental result shows that VLL with the proposed adaptive Kalman filter outperforms under lower SNR conditions or with even insufficient amount of visible satellites comparing with the conventional scalar lock loop(SLL).Both carrier frequency tracking results and navigation solutions from the proposed method are more accurate than those from either fixed－parameter VLL or conventional SLL.

global navigation satellite system;vector lock loop;adaptive Kalman filter

TN967.1

A

0367－6234(2012)07－0139－05

2011－01－22.

赵思浩(1982—)，男，博士，工程师;

陆明泉(1965—)，男，教授，博士生导师;

冯振明(1946—)，男，教授，博士生导师.

赵思浩，zsh@mails.tsinghua.edu.cn.

(编辑 苗秀芝)