低轨卫星紧组合导航UKF方法

姬晓琴，高晓颖

(北京航天自动控制研究所宇航智能控制技术国家级重点实验室，100854 北京)

低轨卫星紧组合导航UKF方法

姬晓琴，高晓颖

(北京航天自动控制研究所宇航智能控制技术国家级重点实验室，100854 北京)

针对紧组合导航系统状态方程及量测方程的非线性，以低轨卫星为应用对象开展了无迹卡尔曼滤波UKF方法研究.给出了惯性系下的系统模型及算法模型，其中姿态直接采用修正Rodrigues参数来表述以避免四元数归一化条件的限制，系统状态更新采用四阶Runge-Kutta法以适应卫星的高速运动;之后通过数学仿真与广义卡尔曼滤波EKF进行了比较分析.结果表明:UKF滤波对于姿态精度明显优于EKF，提高了一个数量级，对于速度、位置精度两者滤波效果相当，但对于运算时间UKF耗时较长.因此实际应用中可根据导航精度与运算时间需求决定是否采用UKF方法.

无迹卡尔曼滤波UKF;紧组合导航;扩展卡尔曼波EKF;低轨卫星

惯性/卫星紧组合导航系统本质上是一个非线性系统，如惯性导航系统误差模型、伪距及伪距率量测方程等，而常规卡尔曼滤波(Kalman Filter，KF)仅适用于线性系统，是一种线性无偏最小方差估计.对于一般的非线性系统，在理论上还难以找到一种严格的递推方法，通常都是用近似方法来解决非线性滤波问题，但都不是最优的.其中扩展卡尔曼滤波(Extended Kalman Filter，EKF)应用最为广泛，但由于线性化误差的影响，EKF是一个次优有偏的估计器.此外还有无迹卡尔曼滤波［1－5］(Unscented Kalman Filter，UKF)、粒子滤波及模型预测滤波等非线性滤波方法.UKF适用于非线性高斯系统的滤波状态估计问题，尤其对于强非线性系统其滤波精度及稳定性较EKF明显提高［6］.

文献［2］对不同精度的惯性仪表与GPS的紧组合导航系统进行了UKF研究，姿态采用四元数表示，但这无法满足滤波过程四元数归一化条件约束;文献［3］基于无人机进行了惯性/GPS/磁力计多传感器融合的UKF研究，给出随着系统维数的增加，UKF的计算量要大于EKF的结论;文献［4］基于运动载体进行松组合导航系统UKF研究，全局姿态用四元数表述，而局部姿态误差用推广的Rodrigues参数定义，这虽然克服了四元数归一化难题，但计算过程比较复杂;文献［7］进行了中高轨卫星的紧组合导航系统研究，姿态处理方法同文献［4］.上述文献基本都有一共性结论:UKF与EKF滤波精度大致相当，只是当初始误差较大时，UKF收敛速度较EKF快，但最终滤波精度是一致的.文献［5］对UAV惯性/GPS/气压高度计组合导航系统进行了研究，状态更新用一阶Euler法，在采用强非线性气压高度计测量模型及强非线性GPS速度位置测量模型(考虑到GPS接收机与IMU安装点不重合)时，UKF滤波精度较EKF提高至少30%，体现了UKF对于强非线性系统的优越性.文献［8］将UKF方法应用在惯性导航初始对准中，但仍旧使用误差状态变量作为系统状态.文献［9］设计了一种新的UT代表点，扩展了UKF算法，仿真表明该扩展算法精度略优于原UKF，但计算量要高20%.

文中针对低轨卫星基于伪距、伪距率的惯性/卫星紧组合导航系统，开展了UKF滤波算法研究，给出了惯性系下的系统模型及算法模型，其中姿态直接采用修正 Rodrigues参数［10－12］作为姿态表述以避免四元数归一化条件的限制，计算过程较文献［4，7］简单，并提高了姿态滤波精度，最后通过数学仿真验证了所提方法对于姿态修正的有效性.

1 无迹卡尔曼滤波UKF

设非线性系统模型为

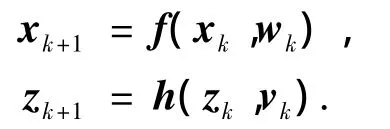
式中:xk为n维状态向量，zk为m维观测向量，wk为q维系统噪声，vk为r维测量噪声，两者均为高斯白噪声，即

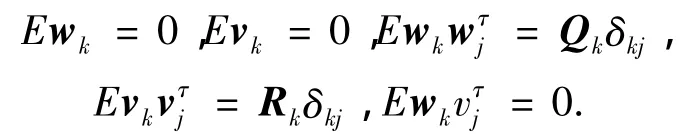
式中:Qk假定为非负定阵，Rk假定为正定阵，假设x0是与{wk}、{vk}都互不相关的随机向量.

首先增广状态向量 Xa=［xτwτvτ］τ，其维数为L=n+q+r，则UKF滤波方程可写为

1)初始化.

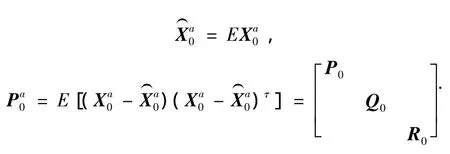
2)计算2L+1个sigma点(采样点).

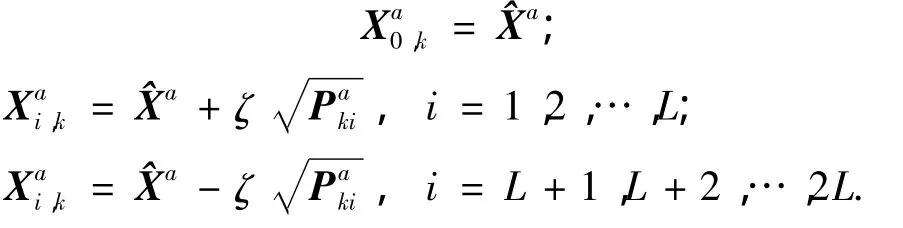
3)状态更新(预测).

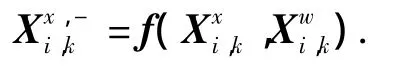
状态变量预测值的均值和方差为

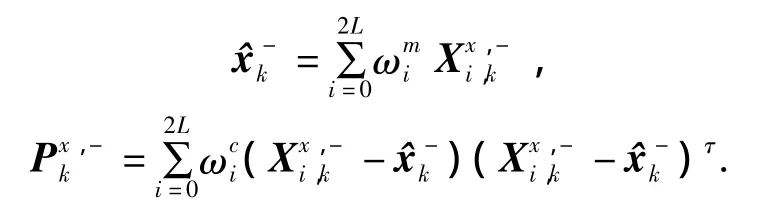
4)量测更新(预测).

根据采样点预测值计算2L+1个预测观测值为

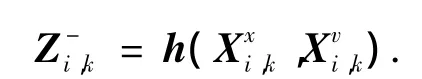
预测观测值的均值和方差为

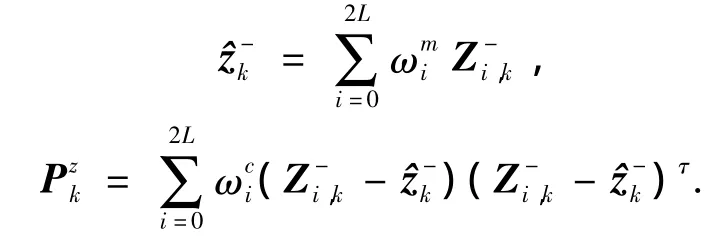
状态量和观测量的互协方差为

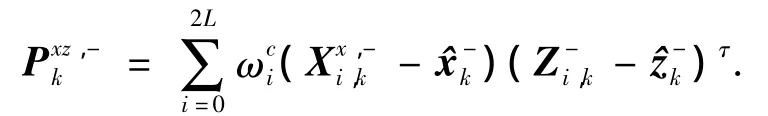
2 紧组合导航系统

2.1 紧组合导航系统状态方程

首先介绍姿态表述的修正Rodrigues参数，它实际上是由姿态四元数推导而来.与绕空间某单位轴e旋转θ角对应的单位四元数q可写为

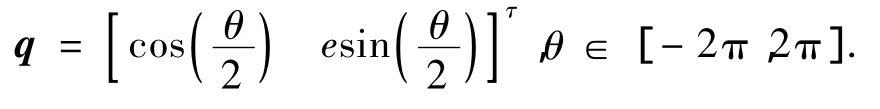
可以看出，R参数旋转角 θ的范围变为(-2π，2π)，在θ=±2π处奇异.

需说明的是，四元数虽然是全局无奇异的姿态表述，但由于四元数不是姿态的最小实现，在滤波递推过程中由因无法始终满足四元数归一化条件而导致滤波误差增大.所以本文直接选取接近全局的最小姿态实现——修正的Rodrigues参数作为姿态表述，既降低了系统维数又保证了滤波精度.

设ω为星体旋转角速度，则姿态四元数满足如下动态方程:

则可导出修正Rodrigues参数的动态方程为

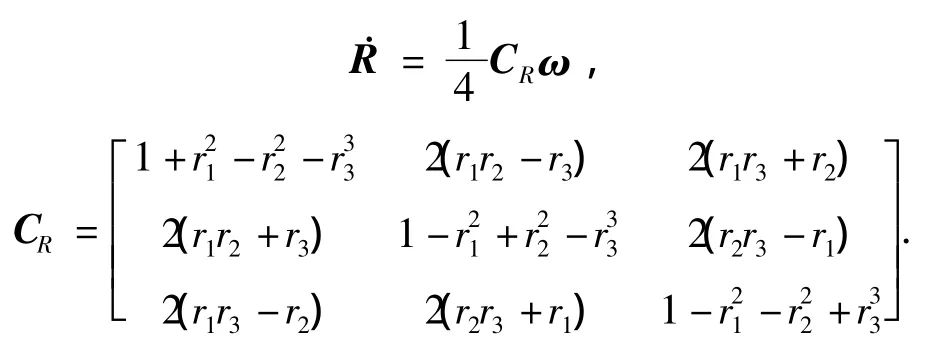
基于修正Rodrigues参数的低轨卫星紧组合导航系统状态方程可写为(只考虑引力，不考虑摄动力):

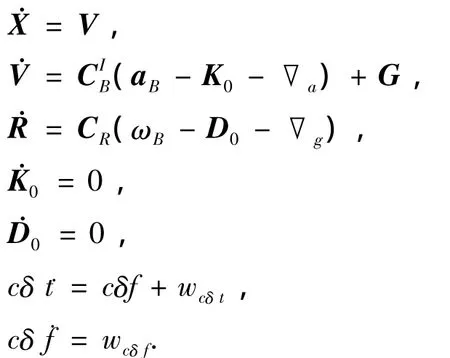
式中:X为位置，V为速度，R为修正Rodrigues参数，K0为加速度计零位误差，D0为陀螺零漂，cδt为与接收机时钟误差等效的距离误差，cδf为与接收机时钟频率误差等效的距离率误差;为弹体系到惯性系的转换矩阵，G为引力加速度;aB、ωB分别为加表、陀螺的测量值;∇a、∇g分别为加速度计、陀螺的测量噪声;wcδt、wcδf为白噪声.

2.2 紧组合导航系统量测方程

伪距、伪距率量测方程为［13］:

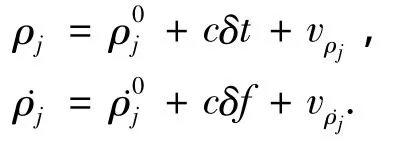
式中:ρj为伪距测量值，˙ρj为伪距率测量值，j代表卫星编号，vρj为伪距测量噪声，v˙ρj为伪距率测量噪声;为惯导计算的第j号导航卫星到接收机的距离，=(X-Xj)τ(V-Vj)/为惯导计算的距离变化率，Xj、Vj为第j颗卫星在惯性系下的位置、速度矢量.

3 数学仿真

3.1 仿真计算条件

1)假设地球为圆形，卫星轨道高度为600 km;

2)滤波器相关参数选取:假设初始状态无误差，假设速度误差 0.1 m/s(1σ)，位置误差20 m(1σ)，姿态 Rodrigues参数误差 2e-4(1σ)，加表零位误差 3 ×10－4g0(1σ)，陀螺零漂0.6(°)/h(1σ)，等效距离误差 300 m(1σ)，等效距离率误差0.03 m/s(1σ)，伪距测量误差50 m(1σ)，伪距率测量误差0.3 m/s(1σ);

3)接收机收星数目:假设低轨卫星上的GPS接收天线的安装方式能保证任一时刻都能收到至少4个卫星信号，即至少有4个伪距、伪距率观测值;

4)系统状态更新:因为低轨卫星在作高速运动，为了保证预测精度以使滤波顺利进行，仿真采用四阶Runge-Kutta法进行系统状态更新.

3.2 UKF仿真结果及分析

基于低轨卫星惯性/卫星紧组合导航系统，本文分别对如下3种滤波方法进行了仿真研究并对其结果进行了比较分析:针对非线性系统方程及量测方程进行了UKF仿真(记为UKF方法1);针对线性化系统方程及量测方程进行了EKF仿真;针对线性化系统方程、非线性量测方程进行了UKF仿真(记为UKF方法2).图1、图2分别给出了EKF与UKF方法1的姿态误差曲线图.仿真结果表明:

1)对于位置、速度、姿态精度，UKF方法2与EKF滤波的效果相当.这说明伪距、伪距率量测方程的线性化对滤波精度的影响不大.

2)对于姿态精度，UKF方法1的效果明显优于EKF滤波，姿态精度由0.8°变为0.03°，提高了一个数量级.分析其原因，应是姿态状态方程的强非线性使得UKF的优势得以发挥.

3)对于位置、速度精度，UKF方法1与EKF滤波的效果相当，这说明速度状态方程的线性化精度足够高，没有体现出UKF的优势.

4)对于仿真运行时间，完成UKF方法2需时约为400 s，而EKF需时约为360 s，这与 EKF大致相当;完成UKF方法1需时约为525 s，耗时较多，这主要是因为卫星在高速运动，而GPS采样信号为1 s一次，故状态更新若用Euler法则预测精度无法保证，仿真中采用四阶Runge-Kutta法虽然保证了精度却导致运算时间增加.

此外，为了进一步考察UKF方法一对姿态的滤波精度，将陀螺精度降低为6°/h(1σ)，在其他滤波条件不变的情况下进行了仿真，仿真结果如图3、图4所示，姿态精度由22°变为0.4°，提高了将近两个数量级，再次验证了本文所用修正Rodrigues参数表述姿态的有效性.

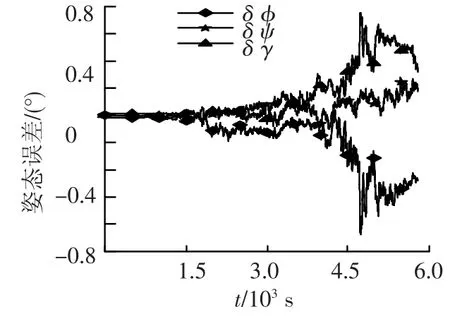
图1 姿态误差曲线(EKF，D0=0.6°/h(1σ)

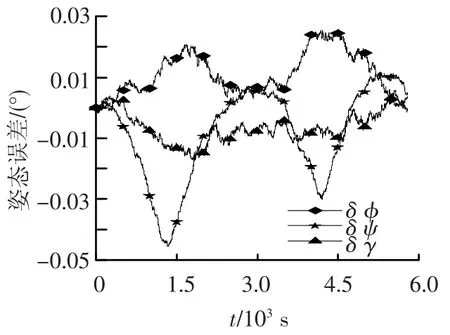
图2 姿态误差曲线(UKF方法1，D0=0.6°/h(1σ)

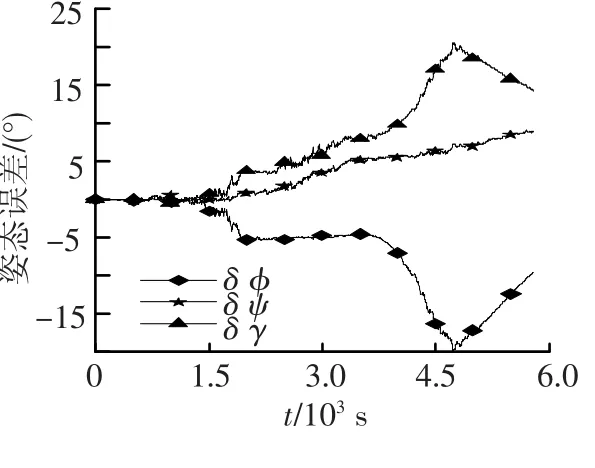
图3 姿态误差曲线(EKF，D0=6°/h(1σ)

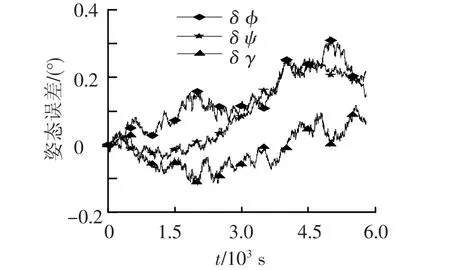
图4 姿态误差曲线(UKF方法1，D0=6°/h(1σ)

4 结论

基于低轨卫星伪距、伪距率惯性/卫星紧组合导航系统，本文针对系统方程及量测方程的非线性，进行了无迹卡尔曼滤波UKF研究，仿真结果显示姿态滤波精度得到大幅提高，表明了直接采用修正Rodrigues参数作为全局姿态表述的有效性，体现了UKF对强非线性姿态运动方程的优势.但是此结果的普遍性和适用性还有待于进一步深入研究.

［1］JULIER S J，UHLMANN J K.A new approach for filtering nonlinear system［C］//Proceedings of the American Control Conference.Washington:Seattle，American Automatic Control Council，1995:1628 －1632.

［2］JAN W，ANDREAS M，JURGEN M，et al.Comparison of Extended and Sigma-Point Kalman Filters for Tightly Coupled GPS-INS Integration［R］.2005，AAIA－2005－6055.

［3］OH Seung-min，JOHNSON E N.Development of UAV Navigation System Based on Unscented Kalman Filter［R］.2005，AIAA-2006-6351，2006.

［4］JOHN L C.Sigma-Point Kalman Filtering for Integrated GPS and Inertial Navigation［R］.2005，AIAA-2005-6052.

［5］VAN D M R，WAN E A.Sigma-point kalman filters for integrated navigation［C］//60th Annual Meeting of the Institute of Navigation.Dayton，OH，United States:Institute of Navigation，2004.

［6］赵琳，王小旭，丁继成，等.组合导航系统非线性滤波算法综述［J］.中国惯性技术学报，2009，17(1):46－52，58.

［7］范利涛.自动转移飞行器自主导航方法研究［D］.长沙:国防科学技术大学，2009:61－80.

［8］张卫明.UKF方法在惯性导航系统初始对准中的应用研究［J］.系统工程与电子技术，2007，29(4):589－592.

［9］李涛.非线性滤波方法在导航系统中的应用研究［D］.长沙:国防科学技术大学，2003:30－39.

［10］WIENER T F.Theoretical analysis of himballess inertial reference equipment using delta-modulated instruments［D］.Cambridge，MA:MIT Dept of Aeronautics and Astronautics，1962:69 －71.

［11］MARKLEY F L.Attitude error reperesentations for Kalman filtering［J］.Journal of Guidance，Control，and Dynamics，2003，26(2):311 －319.

［12］SHUSTER M D.A survey of attitude representations［J］.Journal of the Astronautical Sciences，1993，41(4):439－517.

［13］胡小平.自主导航理论与应用［M］.长沙:国防科技大学出版社，2002:207－210.

UKF for Tightly Coupled Integration in LEO

JI Xiao-qin1，GAO Xiao-ying2

(Beijing Aerospace Automatic Control Institute，National Key Laboratory of Science and Technology on Aerospace Intelligent Control，100854 Beijing，China)

For the nonlinearity of the system dynamic and measurement model in Tightly Coupled Integration of LEO，this article holds research on Unscented Kalman Filter(UKF).The system model and UKF method in inertial frame are introduced.The attitude is represented by modified Rodrigues parameters instead of quaternion for its unit norm constraint，and the state is predicated by the fourth Runge-Kutta technique for satellite＇s high speed.The performance of UKF is compared to Extended Kalman Filter(EKF)by simulations.The results indicate that UKF is better on attitude precision than EKF by one order of magnitude，equal on position and velocity precision，but higher on computation time.

Unscented Kalman Filter(UKF);tightly coupled navigation;Extended Kalman Filter(EKF);low-earth orbit satellite

U666.1

A

0367－6234(2012)07－0135－04

2011－01－25.

姬晓琴(1971—)，女，高级工程师.

姬晓琴，ji－xiaoqin@126.com.

(编辑 苗秀芝)