球形孔洞膨胀动态问题的弹性-损伤力学分析

于雪梅，程 伟，吴 爽

(1.北京航空航天大学航空科学与工程学院，100191 北京;2.黑龙江大学建筑工程学院，150081 哈尔滨)

球形孔洞膨胀动态问题的弹性-损伤力学分析

于雪梅1，2，程 伟1，吴 爽1

(1.北京航空航天大学航空科学与工程学院，100191 北京;2.黑龙江大学建筑工程学院，150081 哈尔滨)

研究了材料还没有出现塑性变形、仅含弹性区和损伤区的球形孔洞动态扩展问题.首先通过对弹性区的研究以及初始损伤分析获得弹性区的场量分布，并给出弹性/损伤区交界处的边界连续条件;然后在自相似假设条件下，推导出动态扩展时损伤区需满足的控制方程;最后通过打靶法进行数值求解.数值分析表明，许多材料参数如ν、n、m都对弹性区和损伤区的场量分布有影响.

孔洞膨胀;损伤力学;自相似假设;打靶法

关于球形孔洞膨胀问题的研究目前广泛应用于材料力学实验、地下爆破、高速穿透、防爆设计以及航空航天工程设计等方面.人们根据研究的内容不同而抽象出不同的受压球形(柱形)孔洞膨胀模型，从而在理论上解决实际工程问题.如Forrestal和Luk［1－3］研究了可压缩弹塑性材料以及应变硬化材料中的球形孔洞膨胀问题;Satapathy［4］研究了脆性陶瓷材料中动态球形孔洞的扩展问题;Durban 和 Masri［5－6］研究了可压弹塑性介质中球形孔洞的动态扩展;刘赵淼等［7］利用球形孔洞模型从理论上研究了泡沫金属材料的动态力学性能及抗侵彻能力，并进行了实验验证;Gao［8－9］提出了两种孔洞膨胀模型以研究弹塑性应变硬化材料的压入变形问题.以上这些研究基本都集中在对于塑性区动态本构方程上，而鲜有对损伤区的研究.实际上，由于变形的连续性，在弹性区到塑性区的过渡中，必然存在损伤区.对此，唐立强、于雪梅等［10－11］针对含损伤区和塑性区的球形孔洞的准静态和动态扩展问题进行了专门研究.本文即主要研究损伤区的动态变形特点.当然，本文所讨论内容要求孔洞膨胀速度m较小(一般小于0.4)，且材料没有出现塑性变形，否则必须考虑塑性区的存在甚至塑性冲击波的作用［12］.

本文建立了含损伤区的球形孔洞膨胀三区模型，采用自相似假设，研究了含损伤区的球形孔洞动态扩展问题，并通过数值计算讨论了材料参数的变化对损伤区场量的影响.

1 含损伤区的球形孔洞动态膨胀模型

含损伤区的球形孔洞动态膨胀模型如图1所示.图中pc为孔洞内压，A为孔洞内径.如取量纲为一的半径ξ=r/A，则取ξi为弹塑性交界，ξw为波前，具体见图示.采用自相似假设［5］，则在稳定扩展阶段，场量对时间的物质导数可以表示为

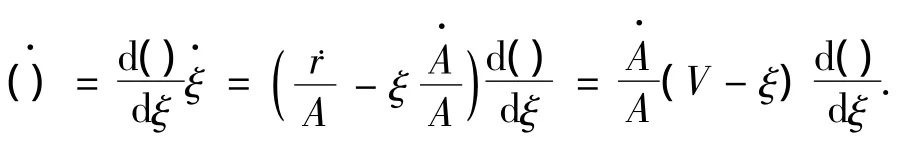
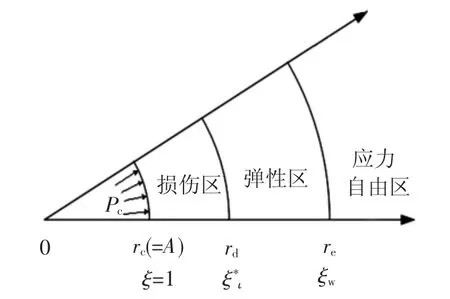
图1 含损伤区的球形孔洞动态膨胀模型

边界条件和连续条件为

1)当 ξ=1时，V=1，Σr=-pc;

2)当 ξ= ξi时，Σre= Σrd，Ve=Vd，ρe= ρd;

3)当 ξ= ξw时，ρ= ρ0，V=0，Σr= Σθ=0.式中:下标e表示弹性区;d表示损伤区;ρ0、ρ分别为变形前、后材料的密度.

2 基本方程

2.1 几何方程

在球形坐标(r，θ，φ)下，几何方程的率形式为

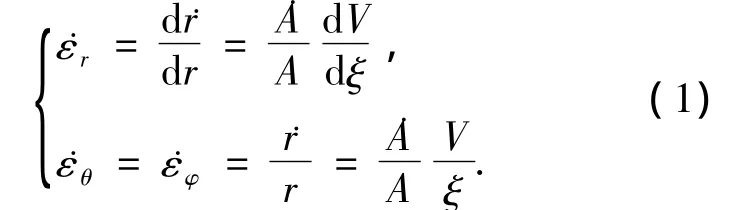
2.2 物理方程

球坐标下损伤区的物理方程为

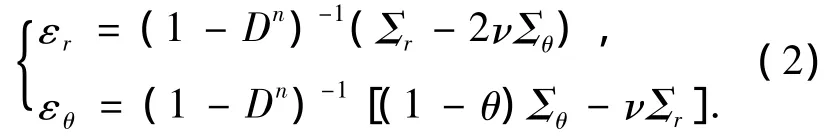
其中D为实际损伤变量，且D=D*-Di0，D*为名义损伤因子，Di0为初始损伤因子.在弹性区，D=0，此时方程(2)化为弹性区物理方程.在弹性区与损伤区边界处，应变状态用Σ表示，初始损伤变量为Di0.n、ν分别为损伤指数和泊松比.

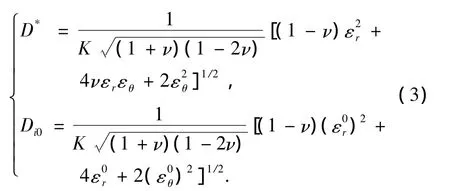
式中K为损伤模量，由材料属性决定.

2.3 运动方程

取无量纲化应力 Σij=σij/E(E为弹性模量).在自相似假设下，运动方程可以表达为［5］

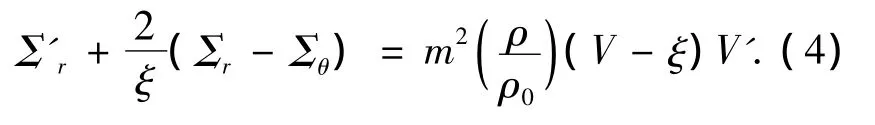
2.4 质量守恒方程

在球对称条件下，质量守恒方程为

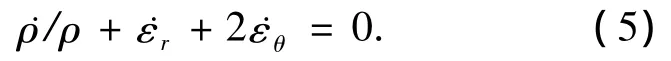
将式(1)带入式(5)并化简得

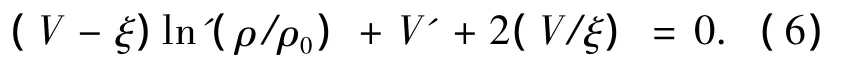
2.5 控制方程

将物理方程(2)两边求导，并用几何方程(1)带入化简，在自相似假设下化简可得到损伤区的控制方程为

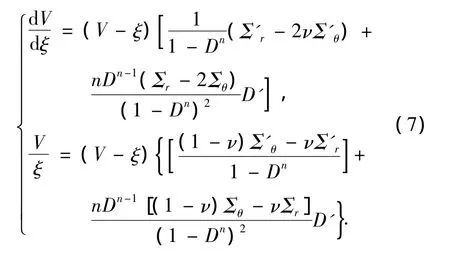
3 求解方法

3.1 弹性区的解

考虑边界条件以及弹性区的应力条件(|Σr|≪1，|Σθ|≪1)，可确定弹性区的解为

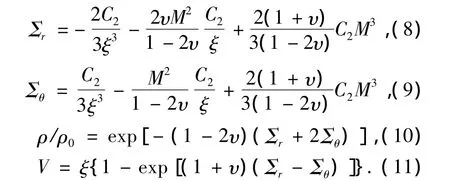
3.2 损伤区的解

综上所述，式(1)～ (2)、(4)、(6)、(7)即构成了损伤区的控制方程组，其中变量有5个，即Σθ、Σr、V、ρ、D，未知数与方程数相同，方程可解.经推导，可确定损伤区求解应力场的方程为

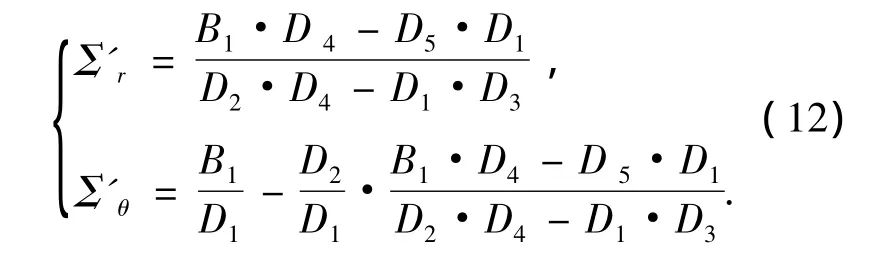
其中:

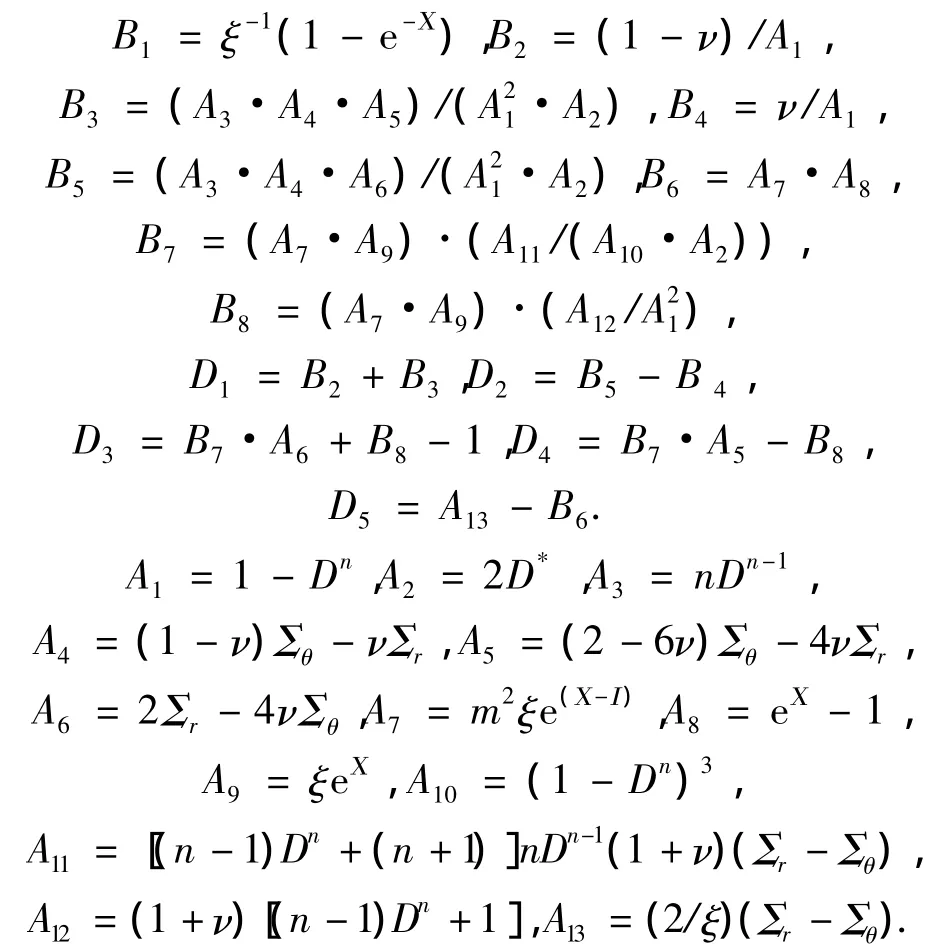
其中D值可由式(3)确定，然后由式(4)、(6)可获得密度场和速度场为

其中:

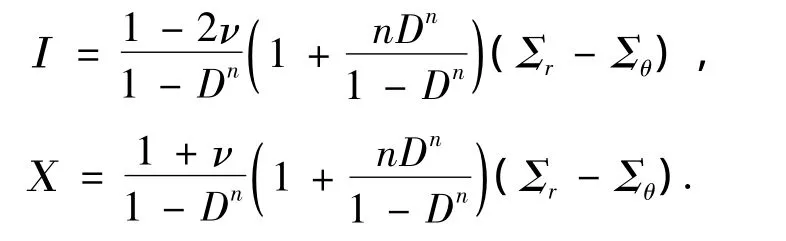
从式(13)、(14)可以看出，当D=0时，两式化为式(10)、(11)，说明在两区交界处，速度场和密度场的分布是连续的.

4 数值计算

从式(8)～(14)可以看出，计算的关键在于设定两区(弹性/损伤)交界处的边界条件，这里存在待定常数C2和两区交界处的位置ξi.在弹性区和损伤区交界处应力满足的初始损伤条件［13］为

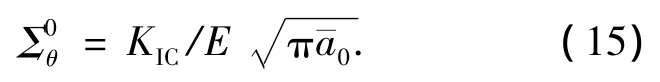
其中KIC为材料的断裂韧度.由式(15)可以确定弹性区待定常数C2.在计算中只需采用打靶法，给定任意的ξi≥1，由方程(8)～(11)可以得出弹性区的全部信息，其与损伤区交界处的场量即可作为求解损伤区的边界条件，进一步由式(12)～(14)进行计算，就可获得损伤区场量分布.检查所得到的损伤区速度场在ξ=1时是否满足边界条件V=1，否则重新进行打靶，直到在ξ=1处满足V=1为止.当ξi确定，就确定了损伤区的范围和损伤区的全部场量的分布.

从弹性区和损伤区的应力场、速度场、密度场表达式(8)～(15)可知，初始裂纹长度¯a0、泊松比ν以及孔洞无量纲化膨胀速度m对弹性区和损伤区的场量分布均有影响，损伤指数n对损伤区分布有影响.对相关参数分别取不同值，通过数值计算可确定各参数对场量的影响.

另外，由前述分析可知，弹性区、损伤区的所有场量分布均是连续的，因此下文只给出损伤区的场量分布.

1)孔洞无量纲化膨胀速度m对场量的影响.取KIC/E=3.8×10-5，K=0.2，n=5，¯a0=2×10-4(m)，ν=0.15，m=0.15/0.35，经计算可获得求解损伤区的初始条件见表1，损伤区的场量分布见图2.

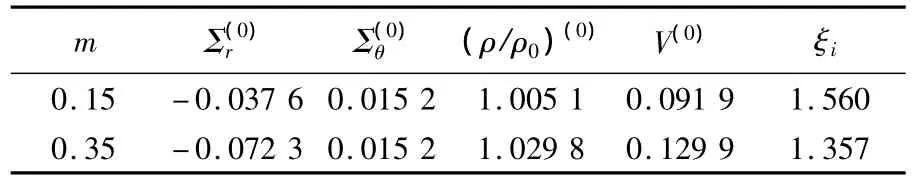
表1 求解损伤区的初始条件(m不同)

从图中可见，m增加，损伤区的连续范围减小，对应同一ξ处，所有场量分布均增大，且在孔洞附近D的变化率明显增大.可以认为孔洞膨胀速度增大时，孔洞内径处的压力增大，因而导致材料更容易受到破坏，使得损伤区的范围减小.图中D为损伤变量，在ξi处为0.

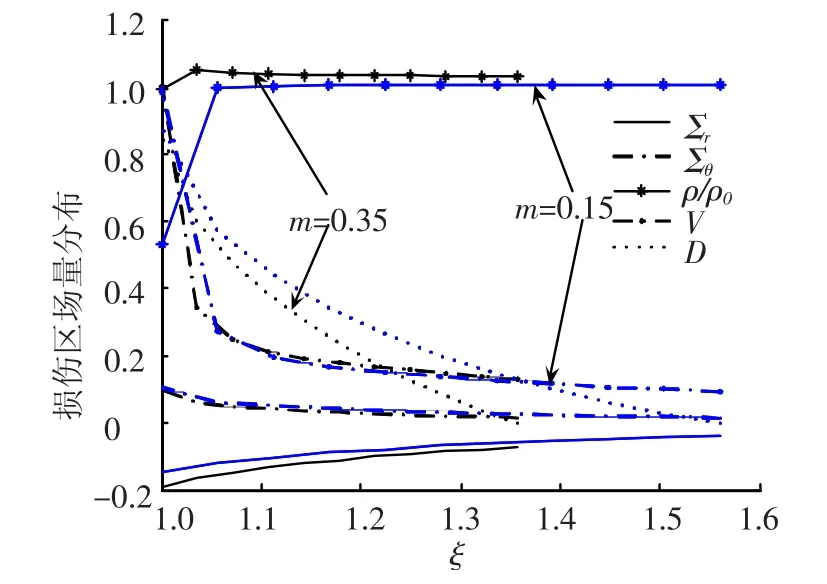
图2 不同m对损伤区场量分布的影响

2)损伤指数n对场量的影响.取KIC/E=3.8×10-5，K=0.2，ν=0.15，¯a0=1×10-4(m)，m=0.15，n=1/5，经计算可得求解损伤区的初始条件见表2，损伤区的场量分布见图3.

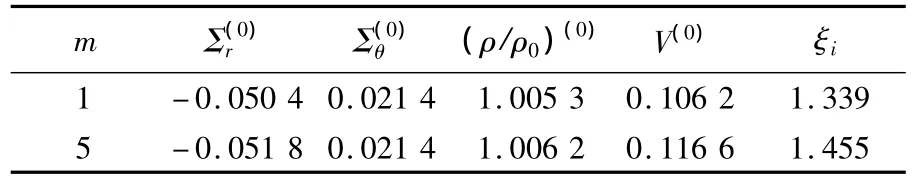
表2 求解损伤区的初始条件(n不同)

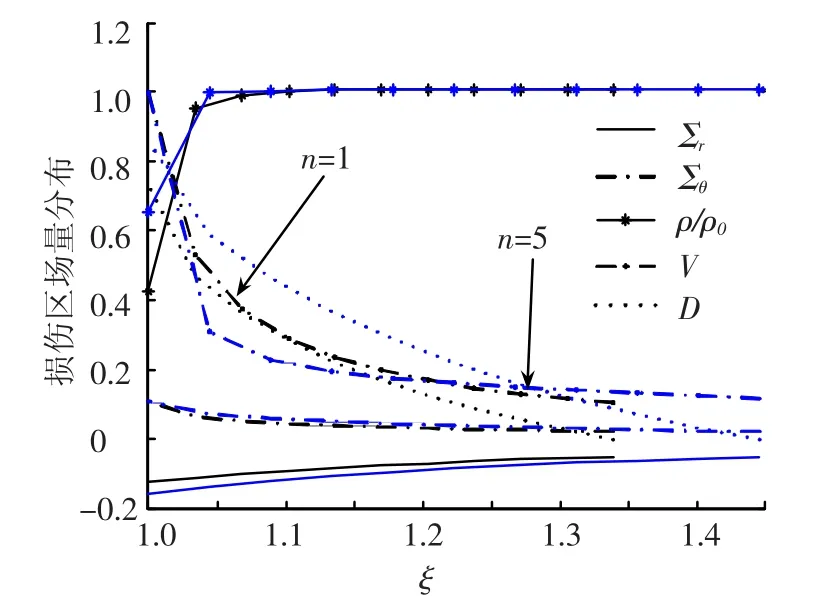
图3 不同n值对损伤区场量分布的影响

从图中可见，n增加，损伤的连续区域增大，即损伤区范围增加，对应同一ξ处，速度场减小、应力场增大.说明随材料韧性增加，导致材料损伤所需的应力越大，同时材料的变形减小，材料抵抗损伤的能力增大.

3)泊松比ν对场量的影响.取KIC/E=3.8×10-5，m=0.15，K=0.2=1×10-4(m)，n=5，ν=0.15/0.35，经计算可得求解损伤区的初始条件见表3，损伤区的场量分布见图4.

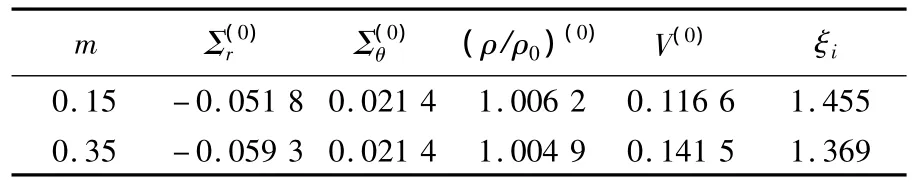
表3 求解损伤区的初始条件(ν不同)

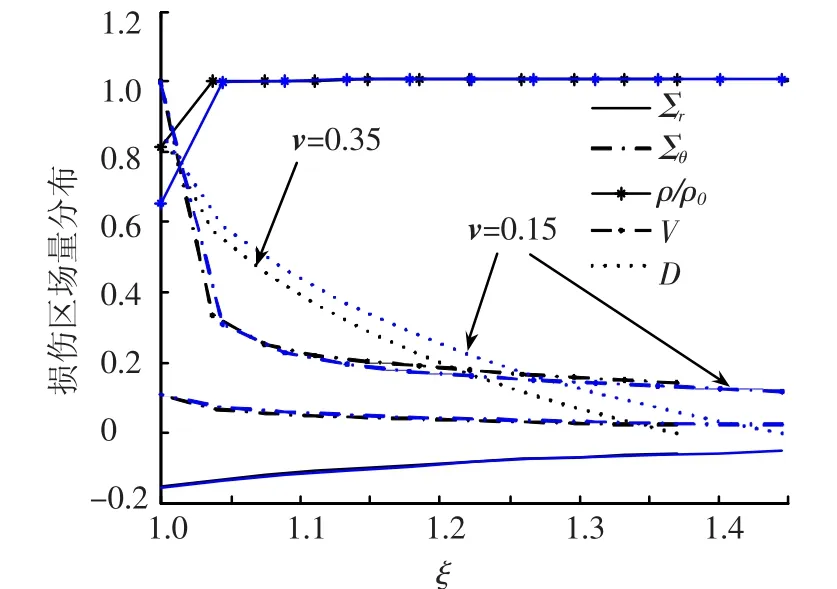
图4 不同ν值对损伤区场量分布的影响

从图中可见，ν增加，损伤区的连续范围减小，对应同一ξ处，除密度变化较小外，其它场量均增大.

总之，孔洞附近损伤区场量变化明显，甚至会出现突然拐点，而远离孔洞处场量变化和缓，趋近弹性区场量分布.

5 结论

1)本文确定了孔洞膨胀速度m较小(一般小于0.4)时包含损伤区的球形孔洞动态膨胀的解析解和数值解，在两区交界处所有场量均连续;

2)在孔洞附近，损伤区的变形比较复杂，场量变化较为剧烈，而在远离孔洞处，场量变化较为和缓;

3)材料参数如泊松比ν、损伤指数n以及球形孔洞无量纲化膨胀速度m等都对弹性区和损伤区的场量分布有影响.ν越大，同一半径处的应力场和速度场增大;m越大，应力场和速度场越大，同时可能出现应变硬化现象;n增加，损伤的连续区域增大，即损伤区范围增加，对应同一ξ处，速度场减小、应力场增大.

［1］FORRESTAL M J，LUK V K.Dynamic spherical cavityexpansion in a compressible elastic-plastic solid［J］.Journal of Applied Mechanics，1988，55:275 －279.

［2］LUK V K，AMOS D E.Dynamic cylindrical cavity expansion of compressible strain-hardening materials［J］.Journal of Applied Mechanics，1991，58(2):334 －340.

［3］FORRESTAL M J，BRAR N S，LUK V K.Penetration of strain-hardening targets with rigid spherical-nose rods［J］.Journal of Applied Mechanics，1991，58(1):7 －10.

［4］SATAPATHY S.Dynamic spherical cavity expansion in brittle ceramics［J］.International Journal of Solids and Structures，2001，38(32/33):5833 －5845.

［5］DURBAN D，MASRI R.Dynamic spherical cavity expansion in a pressure sensitive elastoplastic medium［J］.International Journal of Solids and Structures，2004，41(2):5697－5716.

［6］MASRI R，DURBAN D.Dynamic spherical cavity expansion in an elastoplastic compressible mises solid［J］.Journal of Applied Mechanics，2005，72(6):887 －898.

［7］刘赵淼，高建成.多孔泡沫金属抗侵彻能力研究［J］.北京工业大学学报，2009，35(2):156－161.

［8］GAO X L.Two new expanding cavity models for indentation deformations of elastic strain-hardening materials［J］.International Journal of Solids and Structures，2006，43(7/8):2193 －2208.

［9］GAO X L.Strain gradient plasticity solution for an internally pressurized thick-walled spherical shell of an elastic-plastic material.Mech［J］.Res Comm，2003，30(5):411－420.

［10］YU Xue-mei，TANG Li-qiang，YANG Yong.Static solution on four-region spherical cavity expansion model in the pressure sensitive medium［J］.Journal of Harbin Institute of Technology，2010，17(3):99 －102.

［11］唐立强，于雪梅，吴国辉.压力敏感性材料球形孔洞动态扩展问题［J］.哈尔滨工业大学学报，2010，42(4):665－668.

［12］于雪梅.岩土材料中球形孔洞膨胀问题的力学分析［D］.哈尔滨:哈尔滨工程大学，2010:53－71.

［13］王自强，陈少华.高等断裂力学［M］.北京:科学出版社，2009:14－39.

Dynamic analysis of elastic and damage mechanics on spherical cavity expansion problem

YU Xue-mei1，2，CHENG Wei1，WU Shuang1
(1.School of Aeronautic Science and Engineering，Beihang University，100191 Beijing，China;2.School of Architecture and Engineering，Heilongjiang University，150081 Harbin，China)

The dynamic spherical cavity expansion with damage and elastic area was investigated when distortion is so small that no plastic area arisen.First，by study of elastic region and initial damage，the stress distribution and the continuous conditions in the intersection of damage and elastic regions were given.Then the governing equations to solve the problem of dynamic expansion in the damage zone were deduced.Finally，numerical solutions of the non-linear differential equations were obtained by shooting method.The results show that some material parameters such as v、n、m have influence on the field quantities of elastic and damage regions.

spherical cavity expansion;damage mechanics;self-similar hypothesis;shooting method

O346.5

A

0367－6234(2012)07－0126－04

2011－04－10.

黑龙江省自然科学基金资助项目(A2004-08).

于雪梅(1969—)，女，博士后;

程 伟(1961—)，男，教授，博士生导师.

于雪梅，yuxuemei69@tom.com.

(编辑 张 宏)