采用遗传神经网络的轮轨力建模方法

蔡国强，邢宗义，潘丽莎，程晓卿，秦 勇

(1.北京交通大学 轨道交通控制与安全国家重点实验室，100044 北京;2.南京理工大学机械工程学院，210094 南京;3.广州市地下铁道总公司车辆中心，510320 广州)

采用遗传神经网络的轮轨力建模方法

蔡国强1，邢宗义2，潘丽莎3，程晓卿1，秦 勇1

(1.北京交通大学 轨道交通控制与安全国家重点实验室，100044 北京;2.南京理工大学机械工程学院，210094 南京;3.广州市地下铁道总公司车辆中心，510320 广州)

为解决轮轨力建模问题，提出了一种基于遗传算法和径向基函数神经网络的轮轨力建模方法，该方法基于轨道不平顺输入实现了轮轨力的预测.在径向基函数神经网络的中心、宽度和权值参数上，分别采用遗传算法、最大距离法和最小二乘法来确定，从而提高建模精度并减轻该算法的计算量，实现了快速准确的轮轨力神经网络建模.仿真试验结果表明:提出的轮轨力建模方法具有较高的预测性能.

轨道不平顺;轮轨力;建模;神经网络;遗传算法

随着我国高速客运列车速度和货运列车重载的不断增加，机车车辆与轨道系统之间的相互作用状况越来越严重.作为导致轨道失效、破坏、车辆部件损伤的主要因素，轮轨力越来越成为轨道检测项目的重要内容之一，主要被用来评价列车运行的安全性、平稳性和舒适性［1－2］.目前轮轨力的测量主要是通过测力轮对的方式实现，将应变传感元件安装在车轮上，利用车轮的变形来获取轮轨力［3］.由于测力轮对存在着价格高昂、养护维修成本高等缺点，我国目前仅有极少量的轨道检测车或综合检测列车装备了测力轮对，实现了轮轨力的测量，但这远远不能满足快速发展的高速重载铁路对基于轮轨力安全性评价等需求.

为克服测力轮对的缺点，部分学者采用系统辨识与建模方法，通过对易于实现的轨道不平顺数据的测量，建立轨道不平顺和轮轨力之间的模型，实现轮轨力输出的预测.E.G.Berggren 等［4］通过对轨道、车辆和轮轨关系的分析，构建了轨道不平顺与轮轨力之间的状态方程，可在时域或频域内进行不同速度的长区间的轮轨力仿真计算.F.Xia 等［5－6］提出了基于车辆逆模型的轮轨力预测方法，采用车体横向加速度和垂向加速度、俯仰角和侧滑角，通过构建的车辆逆模型计算轮轨力，实验和仿真结果验证了方法的有效性.上述研究方法在构建状态方程或微分方程组的系统机理模型时，均对复杂的轨道、车辆和轮轨关系进行了简化，忽略了系统的非线性因素，因此建模精度不高，预测的轮轨力与实际输出轮轨力存在较大差异.

神经网络具有任意函数逼近器特性，已经成功地应用到故障诊断、仿真建模、复杂系统控制等多个领域.L.Gualano等［7］采用递归神经网络构建轮轨相互作用模型，模型输入为轨道不平顺参数，包括轨向、超高、水平、三角坑和轨距等，模型输出为轮轨力，仿真实验验证了递归神经网络模型的有效性，但存在模型结构复杂、运算量大和精度亟待提高等问题.S.Nefti等［8］首先采用小波变换减少了输入变量维数，然后采用多层感知器神经网络，构建了轨道不平顺和脱轨系数(横向轮轨力/垂向轮轨力)之间的相关模型，并枚举了不同隐含层和不同隐节点数目情况下神经网络的误差性能，但网络结构(隐节点个数)仅仅通过少量的枚举来确定，且网络参数未进行优化，因此建模精度亟待进一步提高.

本文提出了一种基于遗传算法(Genetic Algorithm，GA)的径向基函数(Radial Basis Function，RBF)神经网络建模方法，用于实现具有复杂非线性特征的轨道不平顺与轮轨力的建模研究.采用专家经验和遍历法相结合来确定神经网络的隐节点个数，然后分别采用遗传算法、最大距离法和最小二乘法确定神经网络的中心、宽度和权值参数.基于实际测量的合武线轨道不平顺数据，在ADAMS/Rail仿真平台上获取轮轨力输出数据，仿真实验结果验证了本文提出算法的有效性.

1 轨道不平顺与轮轨力

轨道对机车车辆起着支撑的作用，保证车辆安全平稳运行.随着时间推移和运量的增加，在轮轨作用力和气候等因素的影响下，轨道会产生越来越严重的各种不平顺，从而降低通过车辆的安全性和舒适性等性能.图1给出了轨道不平顺与轮轨力的示意图，其中轮轨力包括横向力F1和垂向力Fv.考虑到轮轨横向力的成因远比轮轨垂向力复杂，因此本文以轮轨横向力为例，采用轨道不平顺实现轮轨横向力神经网络建模预测.

轨道不平顺采用合武线某区段实测数据，图2给出了向轨道不平顺的输入，自上而下分别为左高低、右高低、左轨向和右轨向.由于现场只能采集到轨道不平顺数据，而缺乏轮轨力的实测数据，因此本文采用ADAMS/Rail动力学仿真软件生成轮轨力数据.ADAMS/Rail软件是20世纪90年代末由美国MID公司在ADAMS软件平台上增加的轮轨关系模块开发的轨道动力学分析的专业软件，通过其交互式图形界面建立模型，可进行机车车辆稳定性临界速度、曲线通过性能、脱轨安全性、牵引/制动特性、轮轨相互作用力、随机响应性能和乘坐舒适性等研究［9］.图3给出了该轨道车辆仿真模型示意图，其中轮轨力为第1轮对的左侧车轮的横向力，轮轨力数据如图4所示，其中输入轨道不平顺包括:左轨高低不平顺、右轨高低不平顺、左轨轨向不平顺、右轨轨向不平顺，共采集1 800组数据，其中前1 000组为训练数据，后8 00组作为检验数据.

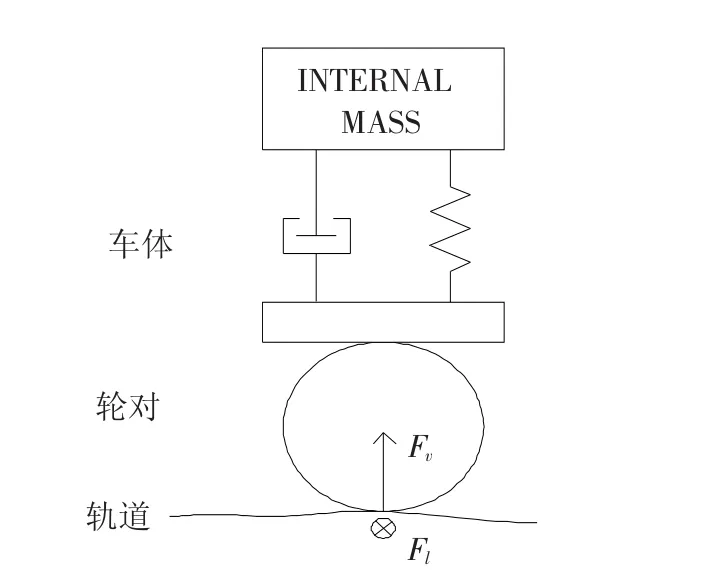
图1 轨道不平顺与轮轨力示意图

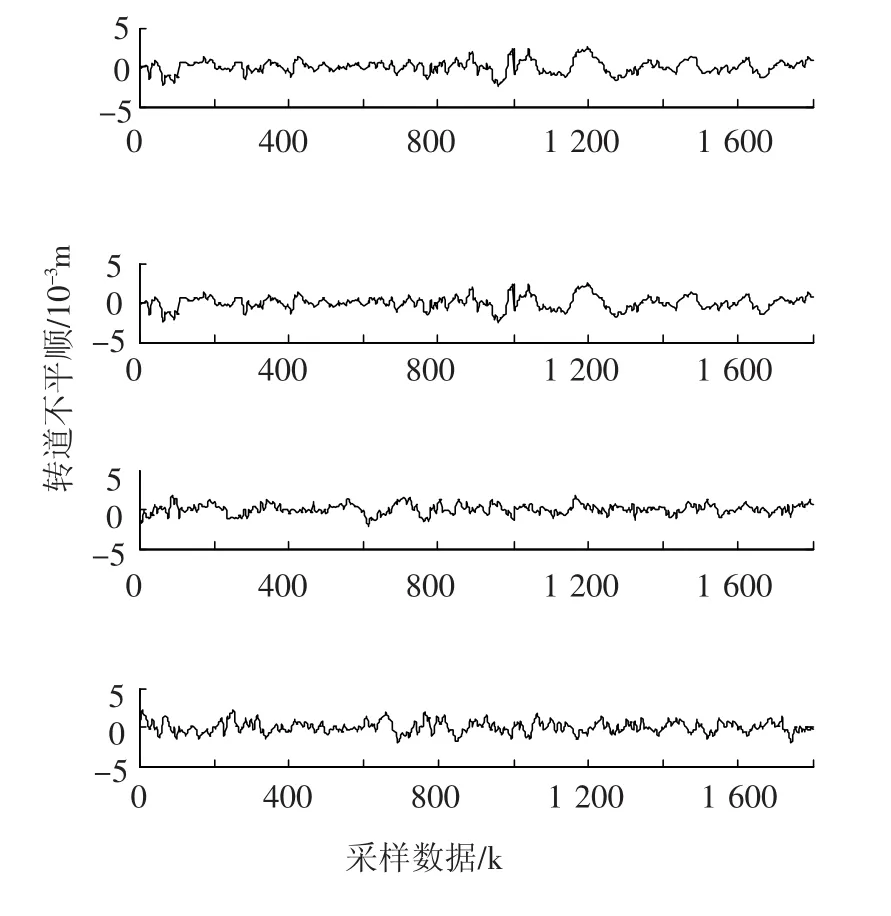
图2 轨道不平顺实测输入数据

图3 ADAMS/Rail轨道车辆仿真模型

图4 轮轨横向力输出数据

2 径向基神经网络

2.1 径向基神经网络

径向基神经网络由输入层、隐层和输出层构成，其结构如图5所示.输入层仅接收输入信号，并将其传递到隐层，隐层的核心为径向基函数，将从输入层接收的信号数学处理后送至输出层，输出层负责将隐层的输出信号加权聚合，从而输出为神经网络的输出信号.

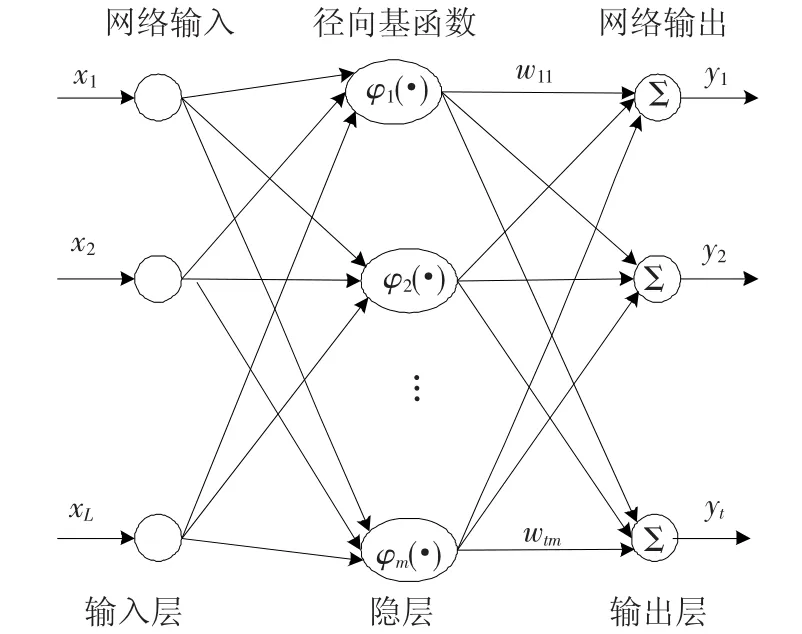
图5 RBF神经网络的结构示意图

RBF神经网络隐层的径向基函数一般为高斯函数，如

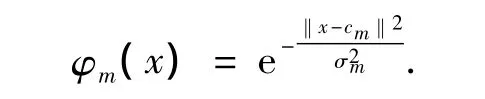
式中:x为输入变量;cm为RBF的中心;‖xcm‖为输入x与中心cm之间欧式距离;σ为RBF的宽度.

RBF神经网络的输出为

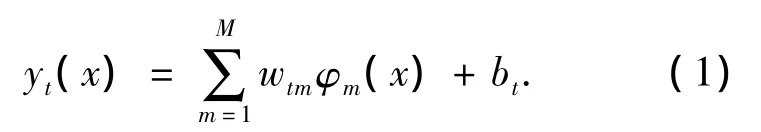
式中:wtm为隐层第m个输出与输出层第t个神经元之间的连接权值;bt为阈值.

在RBF神经网络的训练过程中，需要确定3个参数:RBF的中心cm、宽度σ以及连接权值wtm(阈值bt为权值特例).

在确定RBF的中心参数时，可以随机选定部分数据样本值作为函数中心参数，但由于该方法随机性强因此需要反复试验才可以取得满意值;也可以采用经典的梯度优化法，但该方法计算量大，算法收敛速度慢.因此确定RBF的中心参数一般采用均值聚类(K-Means，KM)算法，它在样本空间内随机初始化中心参数值，然后以样本数据与中心之间的距离总和最小为目标，通过反复迭代优化确定中心参数.在KM算法中，中心参数初始值为随机选择，因此算法容易陷入局部最优，另外在迭代优化过程中没有考虑输出样本信息而仅仅考虑了输入样本信息，因此采用KM算法得到的中心参数难以保证是全局最优的.

GA是一种模拟生物进化论的随机搜索优化算法，具有内在的隐并行性和更好的全局寻优能力.因此基于GA的RBF神经网络得到了众多学者的重视［10－11］.

根据优化参数的多少，可将GA优化RBF神经网络的方法分为两种:1)优化RBF的中心和宽度两个参数［12－15］，本文简称为 GA－2 算法;2)同时优化RBF的中心和宽度、以及隐层和输出层神经元的连接权值3个参数［16－20］，本文简称为GA－3算法.GA－2算法与GA－3算法所优化的参数较多，因此算法较为复杂，搜索空间大，收敛速度慢甚至出现震荡现象，从而难以保证算法收敛到最优解.

本文提出了一种基于GA的RBF神经网络优化方法，简称为GA－1算法.在该算法中，RBF神经网络的中心参数由遗传算法确定，而宽度和权值则采用传统的线性代数法来计算，并在GA优化中心参数时，通过目标函数来实现宽度和权值的间接优化，从而提高神经网络的建模精度，并减轻算法的计算量.

RBF的宽度代表了RBF在输入空间的影响区域，一般采用中心间的距离来衡量，因此本文中宽度取值为中心间最大距离，即对于第i个中心，其宽度参数为

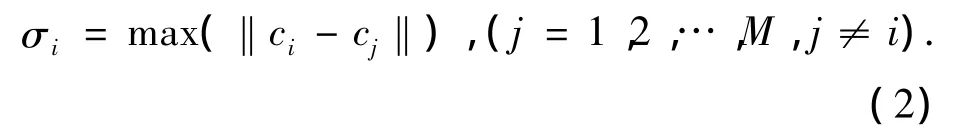
在RBF神经网络中，当RBF的中心和宽度参数确定以后，隐层和输出层之间的连接权值的求解问题可转换为线性优化问题，从而可采用最小二乘法计算权值参数，令

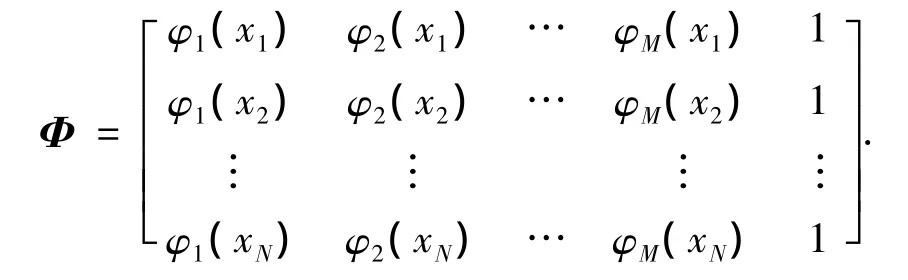
则可以通过计算Φ的伪逆求得权值参数为

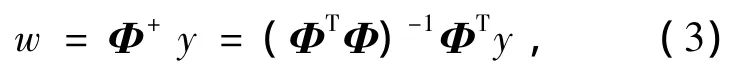
式中:Φ+为Φ的伪逆;y为系统的实际期望输出.

2.2 基于GA的RBF神经网络设计方法:GA－1

RBF神经网络的中心参数是GA－1算法优化的对象.算法从随机初始化的第1个种群开始，按照自然进化原则在每一代中依据适应度函数评价染色体的优劣，并进行选择、交叉和变异遗传操作，产生新的染色体种群，从而逐代进化获得中心参数的最优解.

其中:

1)算法编码.采用实数编码方式，以提高算法的计算速度和精度;染色体编码长度等于神经网络隐节点中心数目.

2)算法操作算子.选择算子采用轮盘赌和精英保留法;交叉算子采用算数交叉，交叉概率为0.8;变异算子采用均匀变异，变异概率为0.05.

3)算法适应度函数.采用神经网络预测输出与目标输出之间的均方根误差作为适应度函数，适应度函数值越小代表对应染色体解码后的问题解越优.

4)算法终止法则.采用进化代数与均方根误差融合法确定算法的终止条件.算法进化代数为300代，在每一代中均选择检验均方根误差最小的解作为代表，从而获得个数为300的解集，最后在解集中选择均方根误差最小的解作为最终解.

算法步骤流程如下:

1)在实数［0，2］范围内随机生成染色体数目为20的初始种群;

2)根据式(2)计算宽度参数，根据式(3)计算权值参数，然后根据式(1)计算网络输出值，并计算染色体适应度函数值;

3)对种群进行选择、交叉和变异的遗传操作，以产生新种群;

4)计算新种群中解码得到的神经网络宽度和权值，然后计算网络输出值和种群染色体的适应度函数值;

5)检查是否满足终止法则，若满足则停止进化过程，并在解集中选择最优神经网络，否则转向步骤3).

3 实验与结果

由于神经网络输入的轨道不平顺信号幅值与输出的轮轨力信号幅值数量级相差较大，可能会造成网络收敛速度慢，因此为提高神经网络学习效率，本文对输入输出数据进行归一化处理为

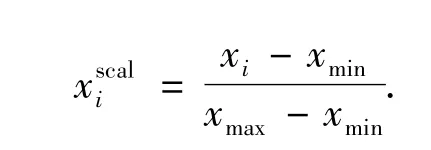
式中:xi为归一化前的变量数据;xmax、xmin分别为对应变量x的最大值和最小值.

本文采用文献［22］的方法确定RBF神经网络的阶次，从而得到神经网络的输入为u(t-2)、u(t-1)、y(t-2)、y(t-1).神经网络的输出为y(t)，其中:u(t)为轨道不平顺输入信号;y(t)为轮轨力输出信号.因此所构造的神经网络为4输入1输出的网络，其训练数据与检验数据分别为998组和798组.

为衡量RBF神经网络的预测性能，本文采用均方根误差(Root Mean Square Error，RMSE)来衡量神经网络的精确性为

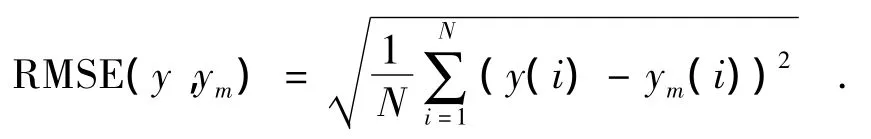
式中:y为目标输出值，即ADAMS仿真模型输出的轮轨力;ym为RBF神经网络的输出值;N为对应的样本数目;RMSE越小，表示神经网络输出越接近目标输出值，其精度越高.

为直观描述目标输出值与神经网络输出值之间的近似程度，本文采用了信号方差比(Variance Account For，VAF)来衡量神经网络输出近似于目标输出的程度为

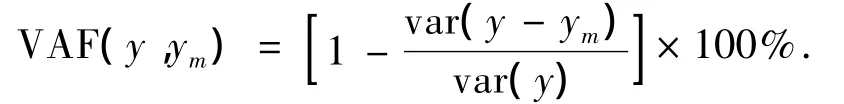
式中:var()为方差操作.信号方差比越大，表示神经网络输出越接近于ADAMS仿真模型输出.

为简便起见，本文KM-RBF为采用KM算法得到的RBF神经网络，GA1-RBF为采用GA－1算法得到的RBF神经网络，GA2-RBF为采用GA－2算法得到的 RBF神经网络，GA3-RBF为采用GA－3算法得到的RBF神经网络.

在RBF神经网络设计过程中，在确定网络类型为4输入1输出后，需要确定隐节点数目.隐节点数目过大容易造成训练过度从而降低网络的泛化能力，隐节点数目过小则无法保证网络的精确性.为确定较优的神经网络隐节点数目，本文基于遍历法原则，采用KM算法和GA－1算法，以步长为2在［6 50］自然数范围内分别得到23个RBF神经网络，然后在该神经网络解集中选择均方根误差最小的网络对应的隐节点数目为最优值.

图6给出了不同隐节点数目下KM算法均方根误差，其中图6(a)为训练误差，图6(b)为检验误差.当隐节点数目从3开始逐渐增大时，KM-RBF的训练误差一直在减小，检验误差先是随着隐节点数目的增加而减小，但当隐节点数目＞28时，其检验误差基本保持不变，因此对于KM算法而言，RBF神经网络的最优隐节点数目应选择＞28.图7给出了不同隐节点数目下GA－1算法均方根误差，其中图7(a)为训练误差，图7(b)为检验误差.当隐节点数目从3开始逐渐增大时，GA1-RBF的训练误差一直在减小，检验误差开始时随着隐节点数目的增加而减小，但当隐节点数目＞30时，其检验误差却开始增大，此时GA1-RBF出现过度训练，因此对于GA－1算法而言，RBF神经网络的最优隐节点数目为30.综合考虑KM算法和GA－1算法性能，并考虑到RBF神经网络的精简性和精确性，本文的RBF神经网络的隐节点数目确定为30.

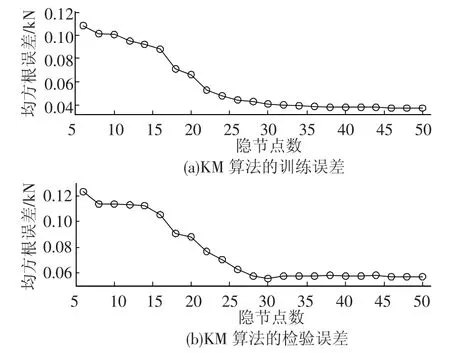
图6 不同隐节点数目下KM算法均方根误差

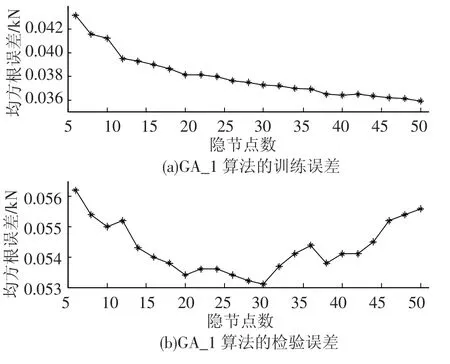
图7 不同隐节点数目下GA－1算法均方根误差

表1比较了采用KM-RBF和GA1-RBF神经网络的性能指标，其中KM-RBF的检验误差为0.056 7，GA1-RBF 的检验误差为 0.053 1，GA－1算法的均方根误差比KM算法降低了6.78%，且信号方差比提高了2.68%，从而证明本文提出的GA－1算法优于KM算法.

为直观地表示两种算法的优劣，图8给出了目标输出轮轨力与KM-RBF神经网络输出轮轨力的回归分析图，图9给出了目标输出轮轨力与GA1-RBF神经网络输出的的回归分析图，从图8、9中可以直观地看出，GA1-RBF神经网络与目标输出值的相关性高于KM-RBF神经网络，这也说明本文提出的GA－1算法优于传统KM算法.

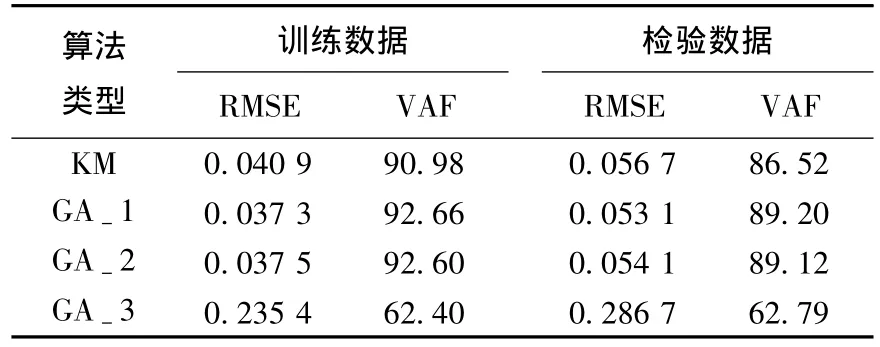
表1 不同算法的性能指标

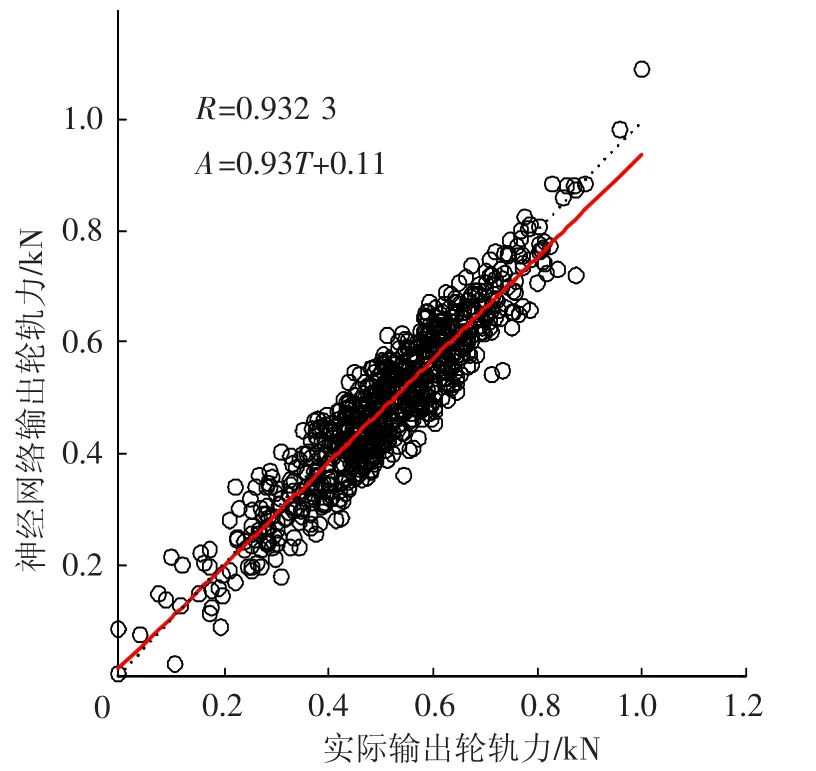
图8 目标输出与KM-RBF神经网络输出轮轨力回归分析

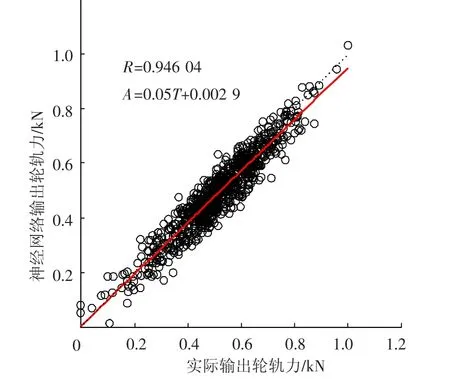
图9 目标输出与GA1-RBF神经网络输出轮轨力回归分析

表1给出了采用 GA－2算法得到的GA2-RBF的性能指标，可见无论是均方根误差还是信号方差比，GA－1算法和GA－2算法得到的神经网络的性能指标均基本一致，因此可以认为，GA－1算法和GA－2算法所得到的神经网络，其性能指标基本一致，但需要说明的是，该结论是建立在对输入输出样本数据进行了归一化处理的前提下，若样本数据未经过归一化，则GA－2算法中宽度参数需要较大的搜索空间从而会降低算法的性能，此时则难以保证GA－2算法会取得与GA－1算法基本相同的性能.

表1给出了采用GA－3算法得到的GA3-RBF的性能指标，其训练误差(0.235 42)与检验误差(0.286 7)均远远大于GA－1算法的训练误差(0.037 3 5)和检验误差(0.053 1)，甚至大于KM-RBF的误差.需要说明的是，在GA－3算法中，权值参数的搜索空间经反复试凑确定为［－10 10］，以保证适中的计算量和参数最优.

为比较不同GA算法的性能，本文对3种GA算法均采用相同的遗传操作和参数，如果采用不同的算法环境，则结论可能会与本文不同.如在GA－3算法中，采用协同进化算法［23］分别进化3个参数则可以得到更为精确的神经网络.

4 结论

1)采用遗传算法优化的RBF神经网络，对复杂的轨道不平顺－轮轨力系统进行建模，试验仿真结果表明了本文构建的RBF神经网络，能够实现基于轨道不平顺的轮轨力预测.

2)采用遗传算法优化RBF神经网络的中心参数，线性代数法辨识其他参数，试验仿真结果及与其他RBF神经网络设计方法的比较，验证了本文提出方法的优越性.

［1］陈建政，陈伟，周艳红.基于径向基函数神经网络的轮轨力检测［J］.振动工程学报，2004，17(Z1):481－483.

［2］邵玉平，陈建政.BP神经网络在测力轮对横垂向桥解耦中的应用研究［J］.铁道机车车辆，2003，23(5):36－38.

［3］常崇义，王成国，李兰，等.连续测力轮对的数字试验研究［J］.铁道机车车辆，2007，27(5):3－5，54.

［4］BERGGREN E G，LI M X D，SPANNAR J.A new approach to the analysis and presentation of vertical track geometry quality and rail roughness［J］.Wear，2008，265(9/10):1488－1496.

［5］XIA Fujie，COLE C，WOLFS P.An inverse railway wagon model and its applications［J］.Vehicle System Dynamics，2007，45(6):583 －606.

［6］XIA Fujie，COLE C，WOLFS P.Grey box-based inverse wagon model to predict wheel-rail contact forces form measured wagon body responses［J］.Vehicle System Dynamics，2008，46(1):469 －479.

［7］GUALANO L，IWNICKI S D，PONNAPALLI P V S，et al.Prediction of wheel-rail forces，derailment and passenger comfort using artificial neural networks［C］//Proceedings of the EURNEX-ZEL Conference.Zilina，Slovakia:［s.n.］，2006.

［8］NEFTL S，OUSSALAH M.A neural network approach for railway safety prediction［C］//Proceedings of 2004 IEEE International Conference on Systems，Man and Cybernetics.Washington，DC:IEEE，2004:3915－3920.

［9］朱浩，刘少军，黄中华，等.ADAMS/Rail虚拟样机技术在车辆系统建模及仿真分析中的应用［J］.交通与计算机.2003，21(5):81－84.

［10］田津，李敏强，陈富赞.复杂样本分类的GA－RBFNN方法［J］.系统工程学报，2006，21(2):163－170.

［11］HARPHAM C，DAWSON C W，BROWN M R.A review of genetic algorithms applied to training radial basis function networks［J］.Neural Computing and Applications，2004，13(3):193 －201.

［12］WHITEHEAD B A.Genetic evolution of radial basis function coverage using orthogonal niches［J］.IEEE Transactions on Neural Networks，1996，7(6):1525－1528.

［13］De LACERDA E G M，LUDERMIR T B，De CARVALHO A C P F.Evolutionary optimization of RBF networks［C］//Proceedings of Sixth Brazilian Symposium on Neural Networks.Washington，DC:IEEE Computer Society，2000:219－224.

［14］赵志刚，单晓虹.一种基于遗传算法的RBF神经网络优化方法［J］.计算机工程，2007，33(6):211－212.

［15］陈明高，石仲堃.遗传算法优化的RBF神经网络确定潜艇排水量和主尺度［J］.中国舰船研究，2006，1(3):38－40，46.

［16］张明君，张化光.遗传算法优化的 RBF神经网络控制器［J］.电机与控制学报，2007，11(2):183－187.

［17］张娟，陈杰，王珊珊.基于遗传算法和RBF网络的番茄生长模型辨识［J］.控制与决策，2005，20(6):682－685.

［18］林叶锦，任光.遗传优化的径向基函数船舶模糊控制器［J］.控制理论与应用，2004，21(6):1036－1040.

［19］向志容，刘国荣.一类非线性系统的自适应控制［J］.计算机仿真，2007，24(9):141－144.

［20］MISHRA S，DASH P K，HOTA P K，et al.Genetically optimized neuro-fuzzy IPFC for damping modal oscillations of power system［J］.IEEE Transactions on Power Systems，2002，17(4):1140 －1147.

［21］童仲志，张媛，邢宗义，等.某装备扫雷犁系统的遗传神经网络建模研究［J］.兵工学报，2010，31(5):650－656.

［22］HE Xiangdong，HARUHIKO A.A new method for identifying orders of input-output models for nonlinear dynamic systems［C］//Proceedings of the American Control Conference.San Francisco:IEEE Press，1993:2520 －2523.

［23］RIVERA A J，ROJAS I，ORTEGA J，et al.A new hybrid methodology for cooperative-coevolutionary optimization of radial basis function networks［J］.Soft Computing，2007，11(7):655－668.

Modelling of wheel-rail force based on genetic neural networks

CAI Guo-qiang1，XING Zong-yi2，PAN Li-sha3，CHENG Xiao-qing1，Qin yong1

(1.State Key Lab of Traffic Control and Safety，Beijing Jiaotong University，100044 Beijing，China;2.School of Mechanical Engineering，Nanjing University of Science and Technology，210094 Nanjing，China;3.Vehicle center，Guangzhou Metro Corporation，510320 Guangzhou，China)

To solve the modelling problem of wheel-rail force，a modelling approach based on the genetic algorithm and radial basis function neural network method is proposed，which can predict the output of wheel-rail force using the input of track irregularities.In order to improve the accuracy of the designed neural network and relieve the computational burden，the centers，widths and weights of the neural network are determined using the maximum distance measure，the least square method and genetic algorithm，respectively.The simulation results indicate that the proposed method can predict wheel-rail force with high precision.

wheel-rail force;track irregularity;modelling;neural network;genetic algorithm

U216;TP183

A

0367－6234(2012)07－0114－06

2011－10－15.

国家自然科学基金资助项目(61074151);国家科技支撑计划资助项目(2011BAG01B05);轨道交通国家重点实验室开放课题资助项目(RCS2009K010);南京理工大学紫金之星资助项目(2010GJPY007).

蔡国强(1969—)，男，副教授;

秦 勇(1971—)，男，教授;博士生导师.

邢宗义，xingzongyi@163.com.

(编辑 张 红)