虚假模态参数识别试验研究

余建新，赵 鹏，谭惠丰

(1.哈尔滨工业大学复合材料与结构研究所，150001 哈尔滨;2.中国航天科工集团伺服技术研究所，210006 南京;3.哈尔滨工业大学分析测试中心，150001 哈尔滨)

虚假模态参数识别试验研究

余建新1，3，赵 鹏2，谭惠丰1

(1.哈尔滨工业大学复合材料与结构研究所，150001 哈尔滨;2.中国航天科工集团伺服技术研究所，210006 南京;3.哈尔滨工业大学分析测试中心，150001 哈尔滨)

为有效识别试验模态分析过程中的虚假模态和轴对称结构中的密集模态，对铝合金薄壳截锥壳卫星适配器样机的动态特性进行试验研究.采用电磁激振器进行激励和压电加速度传感器采集响应，获得结构整体频响函数.采用多项式方法拟合试验曲线，识别结构的模态参数.系统比较单输入单输出、单输入多输出、多输入多输出等方法对频响函数曲线中密集模态参数识别的影响，并对比分析试验结果与有限元仿真结果，进一步识别试验测试曲线中的虚假模态参数.试验结果表明:多输入多输出法更有利于分离轴对称结构的密集模态，试验获得铝合金截锥壳卫星适配器的前10阶固有模态;激振器安装不当导致频响函数曲线中存在虚假模态;对轻质结构进行试验模态分析时，需要考虑激振器的附加质量和附加刚度影响.

试验模态分析;有限元分析;密集模态;虚假模态;参数识别

试验模态分析方法有多种［1－2］，但由于环境噪声污染试验数据以及实验安装方法不当等导致试验数据中存在许多虚假模态信息.轴对称结构中存在多个重叠模态(频率相同，但振型不同的模态)，由于加工误差或质量分布不均匀等因素破坏结构的对称性，重叠模态将以密集模态(频率间隔小，但振型不同的模态)的形式出现.因此如何通过试验手段准确获得结构的模态参数，分析结构的动力学特征具有重要的实用价值.

新型卫星适配器是截锥壳结构，在航天器发射过程中得到广泛应用［3］.Thomas［4］提出截锥壳连接多个有效载荷概念设计，进行一箭多星发射.理论分析方面，Chen［4－5］提出基于可靠性分析的截锥壳卫星适配器设计方法，用于整星隔振系统设计;Chai［6］采用做动器对截锥壳振动特性进行主动控制研究;Li［7］采用瑞利－里茨法计算铝锥壳固有频率和受迫响应，但只能对简单的结构求解析解.Sweedan［8］试验研究截锥壳在横向激励下结构的时变特性，王威远［9］对蜂窝截锥壳的减振特性进行试验研究，陈阳［10］对含铝合金截锥壳结构的整星隔振系统的阻尼特性进行研究.上述试验方案主要评估锥壳结构的减振、隔振特性.由于没有测试力信号，只获得加速度响应信号，无法获得结构的频响函数，所以无法分析结构的固有频率、阻尼比、振型等模态参数，并且没有考虑结构中存在虚假模态信息.

本文对铝合金截锥壳卫星适配器样机的动态特性进行试验研究.采用电磁激振器进行激励和压电加速度传感器采集响应，通过动态信号采集分析仪获得结构整体频响函数，然后采用多项式方法拟合试验曲线，进一步识别结构的模态参数.系统比较单输入单输出、单输入多输出、多输入多输出等方法对密集模态结构频响函数参数识别的影响，最后将试验结果和有限元结果进行对比分析.

1 理论分析

离散多自由度系统的受迫振动微分方程为

［M］{¨u}+［C］{˙u}+［K］{u}={F(t)}.其中［M］为质量矩阵，［C］为阻尼矩阵，［K］为刚度矩阵，{F(t)}为惯性力矩阵，{u}为位移矩阵.当［C］=0，{F(t)}=0 时，方程变为

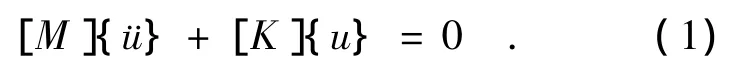
公式(1)为多自由度系统的自由振动方程.

假设微小幅度振动情况下，上述方程组的解为

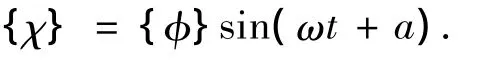
其中，

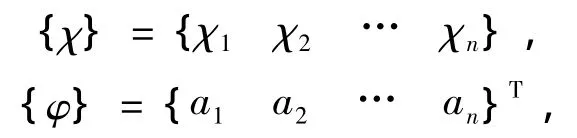
将解代入微分方程得

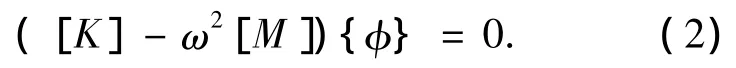
如果方程组中a1，a2，…an不全为零，则要求其系数行列式的值等于零，即

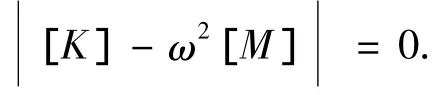
求解系统的固有频率ωi，代人公式(2)得到对应的特征向量{φ}也就是主振型.

2 试验装置

铝合金截锥壳几何模型如图1所示，由4部分组成.其中两相邻曲面之间通过铝条拼接而成，并通过铆钉连接加固，其中厚度为2 mm.

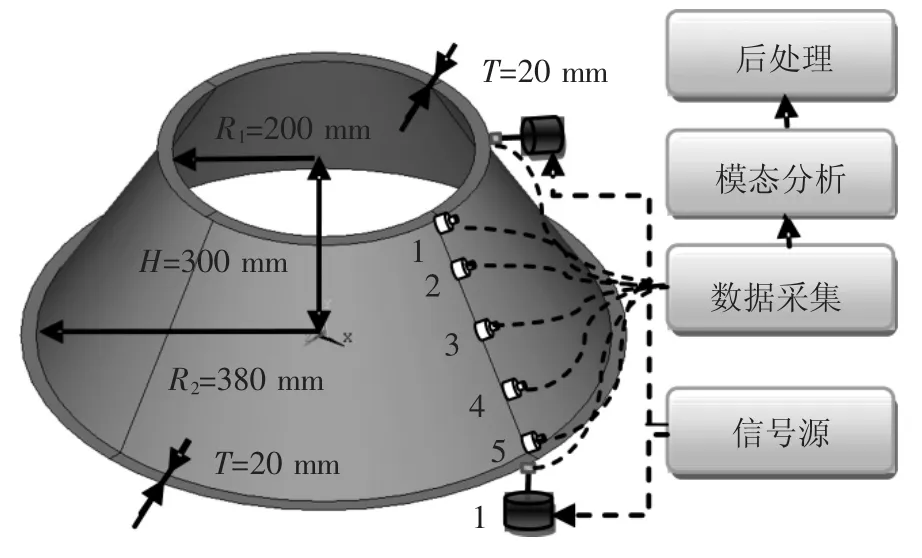
图1 几何模型

试验设备:江苏联能电子公司CA－YD－107压电传感器 5个，B＆K8200力传感器 2个，YE5853电荷放大器5个，JZK－5N激振器激振2个，美国Nicolet公司的COMPASS动态数据采集分析仪1台，MESCOPE模态分析软件1套.

试验过程:连接振动测试仪器并进行调试.在激振器和截锥壳之间安装力传感器，通过顶杆调节激振器和截锥壳的距离，在结构表面安装加速度传感器.信号源发出信号激励电磁激振器，同时将力通道和加速度通道信号连入动态数据分析仪器.采集力传感器和加速度传感器的时间响应信号，经过加窗、滤波、采样、A/D转换、FFT变换等数字信号处理过程，在频率域分析结构的动态特征.获得结构的频响函数后，导入到模态分析软件，通过多项式曲线拟合试验曲线，识别结构的模态参数.

3 试验

3.1 单输入单输出

采用电磁激振器进行激励的优点是信号源可控.常用信号源有正弦快速扫频信号(Chirp)，正弦慢速扫频信号(Sine Sweep)，白噪声信号(White Noise)，伪随机信号(Pseudo Random)等.对不同激励信号对结构频响函数测定的影响进行试验分析.

数据采集分析参数设置为:分析带宽0～300 Hz，频域谱线400线，时域点数1 024点，频域平均100次，加HANNING窗.对白噪声信号重叠50%.Chirp扫频电压幅值1 V，扫频范围5～500 Hz，周期 50% .

图2为不同激励信号对频响函数测试的影响.由图2可知，共振频率有细微差别.正弦快扫法得到的相干曲线质量相对较好，各频响函数共振峰值处相干函数值大于0.9.由于该结构为中心对称结构，频响函数曲线存在比较明显的密集模态.

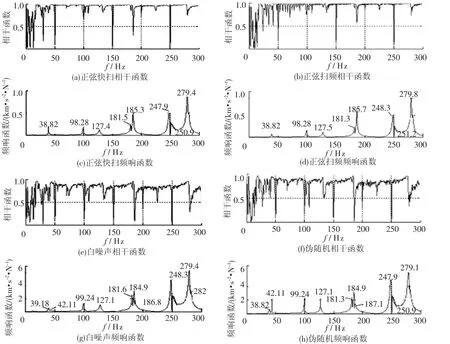
图2 不同激励信号下频响函数和相干函数

3.2 单输入多输出

采用正弦快扫对结构进行激励，采集激振器处力传感器和3个加速度传感器响应，得到的频响函数进行局部细化，结果如图3所示，结构的密集频率特性更加明显.其中H21，H31，H41分别表示不同位置(2#，3#，4#)加速度传感器与激振器(1#)之间频响函数.

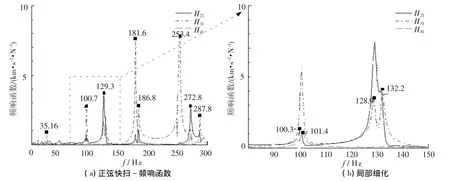
图3 正弦快扫频响函数与局部细化

3.3 多输入多输出

采用2个激振器分不同方向进行激励，并将锥壳表面均匀划分40个点，移动加速度传感器位置，采集各点的频响函数.由于结构存在多个密集频率，将所有的频响函数进行集成并进行包络分析时，频率间隔太小的两个频率容易变为单个频率进行处理，需要仔细处理.

4 参数识别

将多输入多输出得到的频响函数导入模态分析软件，采用峰值提取法识别分析频率带宽内的固有频率数目，采用多项式法拟合试验曲线，提取模态参数.各模态之间的模态置信准则［11］如图4，非对角线MAC值相对较小，说明各模态相互影响小.

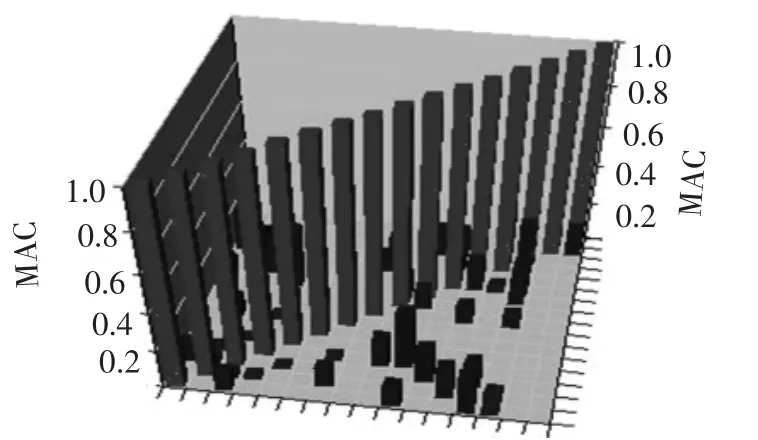
图4 模态置信准则

用有限元软件进行仿真分析.采用shell93单元，铝合金材料力学参数为:弹性模量7.2e10 Pa，泊松比0.33，密度2 700 kg/m3.

试验测试和有限元仿真得到的截锥壳固有频率值如表1所示.前6阶仿真模态振型图如图5所示.

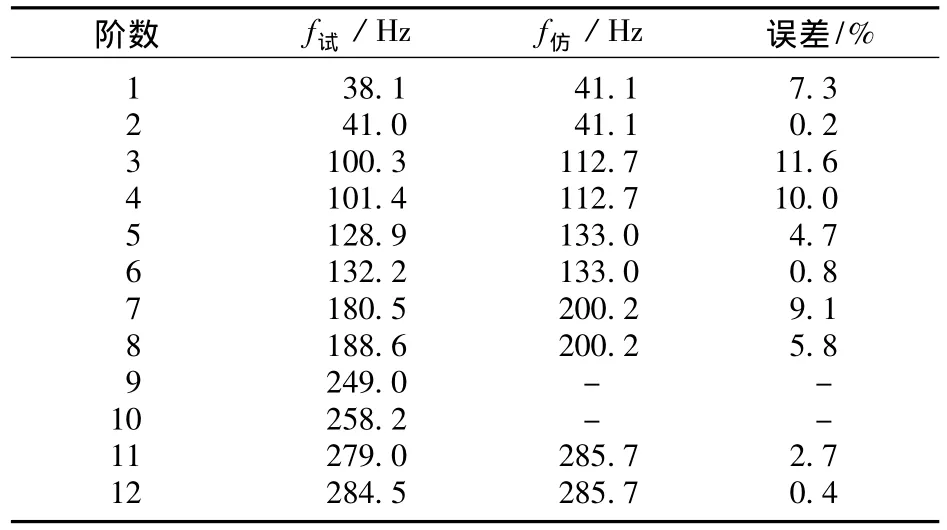
表1 试验和仿真固有频率值

图5 模态振型图

为进一步分析原因，采用锤击法对结构进行试验模态分析，设置力/指数窗，取频域平均10次.采集任意3点的频响函数，结果如图6所示，在250 Hz处没有共振峰值.经过对比分析可以确定，250 Hz是完全由激振器安装引起的虚假模态，可见单一的模态置信准则并不能有效识别频响函数中的虚假模态信息.

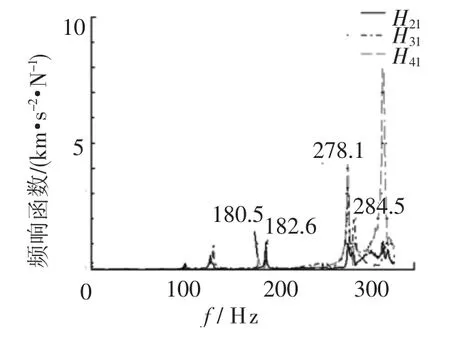
图6 锤击法频响函数曲线

5 结论

1)单输入单输出法可能造成漏频，单输入多输出法和多输入多输出法综合多个响应的叠加，更适合复杂结构，并且有利于分离轴对称结构的密集频率.

2)采用激振器虽然具有信号可控的优点，但是对结构产生附加质量和附加刚度影响，特别是对轻质柔性结构动态特性分析不容忽视.

3)由于激振器安装不当，导致频响函数中包含虚假频率.单一的模态置信准则，无法识别虚假模态.

4)有限元仿真分析结果有利于确定激振器、传感器的安装位置，并对试验结果进行验证.

［1］曹树谦，张文德，萧龙翔.振动结构试验模态分析［M］.天津:天津大学出版社，2002:50－77.

［2］沃德.海伦，斯蒂芬·拉门兹，波尔·萨斯，等.模态分析理论与试验［M］.北京:北京理工大学出版社，2001:257－268.

［3］王跃宇，冷力强，李志，等.星箭适配器PAF隔振技术的进展［J］.航天器环境工程，2007，24(1):43－46.

［4］THOMAS G R，FADICK C M，FRAM B J.Launch vehicle payload adapter design with vibration isolation features［C］//Proceedings of SPIE.San Diego:SPIE，2005，5760:35－45.

［5］CHEN Y，FANG B，YANG T Z，et al.Study of wholespacecraft vibration isolators based on reliability method［J］.Chinese Journal of Aeronautics，2009，22(2):153 －159.

［6］CHAI W K，HANA Y，HIGUCHI K，et al.Micro-actuation characteristics of rocket conical shell sections［J］.Journal of Sound and Vibration，2006，293(2):286－298.

［7］LI F M，KISHIMOTO K，HUANG W H.The calculations of natural frequencies and forced vibration responses of conical shell using the Rayleigh-Ritz method［J］.Mechanics Research Communications，2009，36(5):595 －602.

［8］SWEEDAN A M I，DAMATTY A A.Experimental and analytical evaluation of the dynamic characteristics of conical shells［J］.Thin-Walled Structures，2002，40(5):465－486.

［9］王威远，王聪，邹振祝.蜂窝锥壳结构动力学特性试验研究［J］.振动与冲击，2007，26(7):164－168.

［10］陈阳，方勃，张业伟，等.整星隔振器性能及阻尼可靠性实验分析［J］.哈尔滨工业大学学报，2010，44(1):13－15.

［11］ALLEMANGE R L.The modal assurance criterion twenty years of use and abuse［J］.Sound and Vibration，2003，8(1):14－21.

Experimental research on false modes parameter identification

YU Jian-xin1，3，ZHAO Peng2，TAN Hui-feng1

(1.Center for Composite Materials and Strutures，Harbin Institute of Technology，150001 Harbin，China;2.Servo Technology Institutes，China Aerospace Science and Industry Corporation，210006 Nanjing，China;3.Center for Analysis and Measurement，Harbin Institute of Technology，150001 Harbin，China)

To discern false modes during experimental modal analysis process and identify dense modes in axial symmetrical structures，the dynamic properties of truncated conic aluminum alloy thin shell satellite adaptor was experimental investigated.Electromagnetic vibration generators were used for exciting structures，and piezoelectric accelerometers for measuring the corresponding response.Polynomial method was applied for fitting experimental frequency response functions and identifying modal parameters.The effects of different methods between single input single output(SISO)，single input multiple output(SIMO)，and multiple input multiple output(MIMO)were evaluated systematically，both experimental and numerical analysis results were compared to recognize false modes.The experimental results show that the MIMO method helps in splitting dense modes in axial symmetry structures，and the former 10 modes of satellite adaptor were clearly identified.However，improper exciter fixation results in false modes in frequency response function.For experimental modal analysis of lightweight structures，special attention should be paid on additional mass and stiffness due to exciter fixation.

experimental modal analysis;finite element analysis;dense modes;false modes;parameters identification

V416.2

A

0367－6234(2012)07－0047－04

2011－06－01.

新世纪优秀人才支持计划资助(NCET－08－0150).

余建新(1984—)，男，博士研究生;

谭惠丰(1969—)，男，教授，博士生导师.

余建新，yujianxin03242@163.com.

(编辑 杨 波)