几何参数对旋转薄壁圆柱壳振动特性的影响

刘彦琦，褚福磊

(清华大学 精密仪器与机械学系，北京 100084)

圆柱壳是典型的工程结构，广泛应用于航空、航天、机械及船舶等领域，其动力学行为广受关注［1－5］。圆柱壳的固有频率特性是系统振动分析的基础与关键，但在圆柱壳频率特性研究中，细长圆柱壳频率特性研究较多，短粗圆柱壳频率特性则较少关注。鉴于此，本文将研究几何参数(厚度与半径之比、半径与长度之比)对圆柱壳频率与振型比的影响，重点分析半径大于长度的圆柱壳振动特性。

1 振动方程

圆柱壳动力学模型示意图见图1，圆柱壳以角速度Ω转动，其中厚度为h，半径为r，长度为L。采用曲坐标系oxθz描述旋转圆柱壳系统，u，v与w分别为圆柱壳在x，θ与z方向位移。

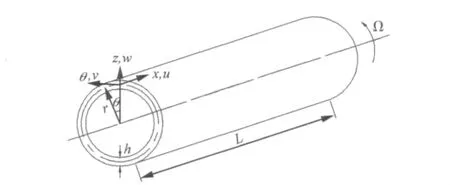
图1 旋转圆柱壳模型示意图Fig.1 Mode of rotating circular cylindrical shell

基于Love薄壳理论，考虑惯性力、科氏力与离心力，采用Hamilton原理建立旋转薄壁圆柱壳振动微分方程如下:

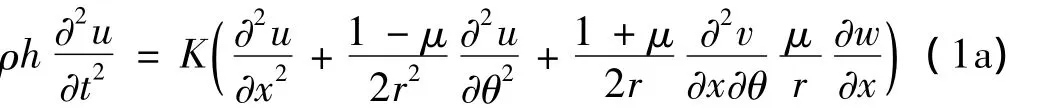
其中:ρ为密度，E为弹性模量，μ为泊松比，K=Eh/(1－μ2)为薄膜刚度，D=Eh3/12(1－μ2)为弯曲刚度。

上述方程描述了旋转薄壁圆柱壳在u，v和w三个方向的振动，其中等式左端包含惯性力项、科氏力项及离心力项，右端为刚度项。

2 振动特性分析

将圆柱壳的振型表示为轴向梁函数与周向三角函数组合形式，系统的解可表示为［6］:

其中，φ(x)=a1cosh(λmx/L)+a2cos(λmx/L)－σm·［a3sinh(λmx/L)+a4sin(λmx/L)］离散系统Galerkin得:

整理得:

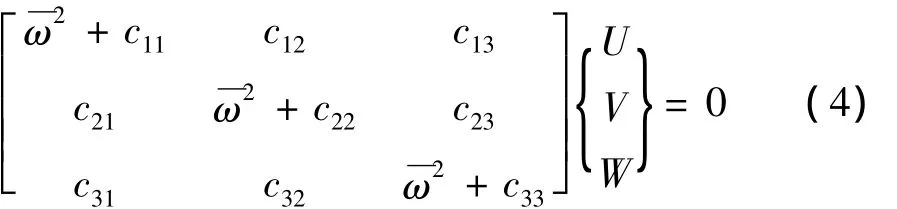
由方程(4)有非平凡解的条件可得到系统频率方程:

其中，βi为系数。

基于上述分析，本节将针对五种不同边界条件，探讨几何参数对旋转圆柱壳固有频率特性的影响。

简支－简支(S－S):

固支－简支(C－S):

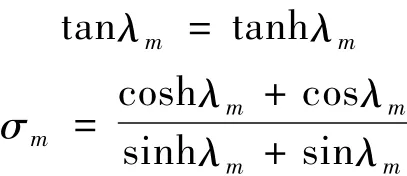
固支－自由(C－F):

自由－简支(F－S):

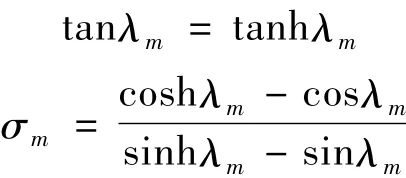
固支－固支(C－C):

旋转圆柱壳系统参数选为:μ=0.3，E=1.078×105MPa，ρ=4.5×103kg/m3，N=6000 r/min;针对振型(m=1，n=6)的情况，基于上述给定参数，分别分析几何参数对旋转圆柱壳固有频率和振型比的影响。

图2 h/r对频率特性的响应Fig.2 Frequency characteristic for different h/r

厚度与半径之比(h/r)是描述圆柱壳形状的重要指标之一，针对五种不同边界条件情况，厚度与半径之比对圆柱壳固有频率的影响如图2所示。由图可知，随着h/r的增大，五种边界条件下圆柱壳固有频率值均单调增加，且变化幅度较小。

半径与长度之比(r/L)是描述圆柱壳形状的重要指标之二，半径与长度之比对圆柱壳固有频率的影响，如图3～图6所示。由图可知，在0.01＜r/L＜0.1时(图3)，除C－F时固有频率随r/L的增大而减小外，其它几种边界情况固有频率均随r/L的增大而增大;且频率值按C－C，F－S，C－S，S－S，C－F依次由大到小。

在0.1＜r/L＜0.6时(图4)，除 C －F时固有频率随r/L的增大而减小外，其它几种边界情况时固有频率均随r/L的增大而增大。另外，当r/L＞0.4时，五种边界条件下圆柱壳固有频率值的大小排序变化明显，即按F－S，S－S，C－S，C－C，C－F的顺序圆柱壳固有频率值依次由大到小。由此可见，随着半径与长度之比的逐渐增大，不仅圆柱壳固有频率值的大小在变，五种边界圆柱壳固有频率值的大小排序也在变。

图3 0.01＜r/L＜0.1时频率特性Fig.3 Frequency characteristic 0.01 ＜r/L ＜0.1

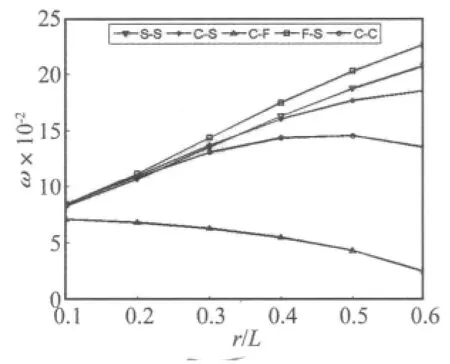
图4 0.1＜r/L＜0.6时频率特性Fig.4 Frequency characteristic 0.1 ＜ r/L ＜0.6

图5 0.1＜r/L＜1时频率特性Fig.5 Frequency characteristic 0.1＜r/L＜1

当r/L增大到0.6时，C－F边界条件下圆柱壳的固有频率突然增大，且远大于其它几种边界情况下的圆柱壳固有频率值，见图5。

图6 0.01＜r/L＜4时频率特性Fig.6 Frequency characteristic 0.01 ＜ r/L ＜4

图6表述了在0.01＜r/L＜4范围内，半径与对比系统频率系数的影响。由图可知，r/L较小时，即长度大于半径的圆柱壳，系统的固有频率较小;对于长度小于半径的短圆柱壳，系统的频率远大于细长圆柱壳的固有频率，并分别在 r/L 值为 1.5，2.，2.5，3 时有最大值，然后随着r/L的增大而减小，但依然大于细长圆柱壳的频率值。由上述分析得知:厚度与半径之比对圆柱壳固有频率的影响较小，半径与长度之比对圆柱壳的固有频率影响显著。

除固有频率特性外，振型比是描述振动形态另一个主要因素。旋转圆柱壳系统的振型比为:

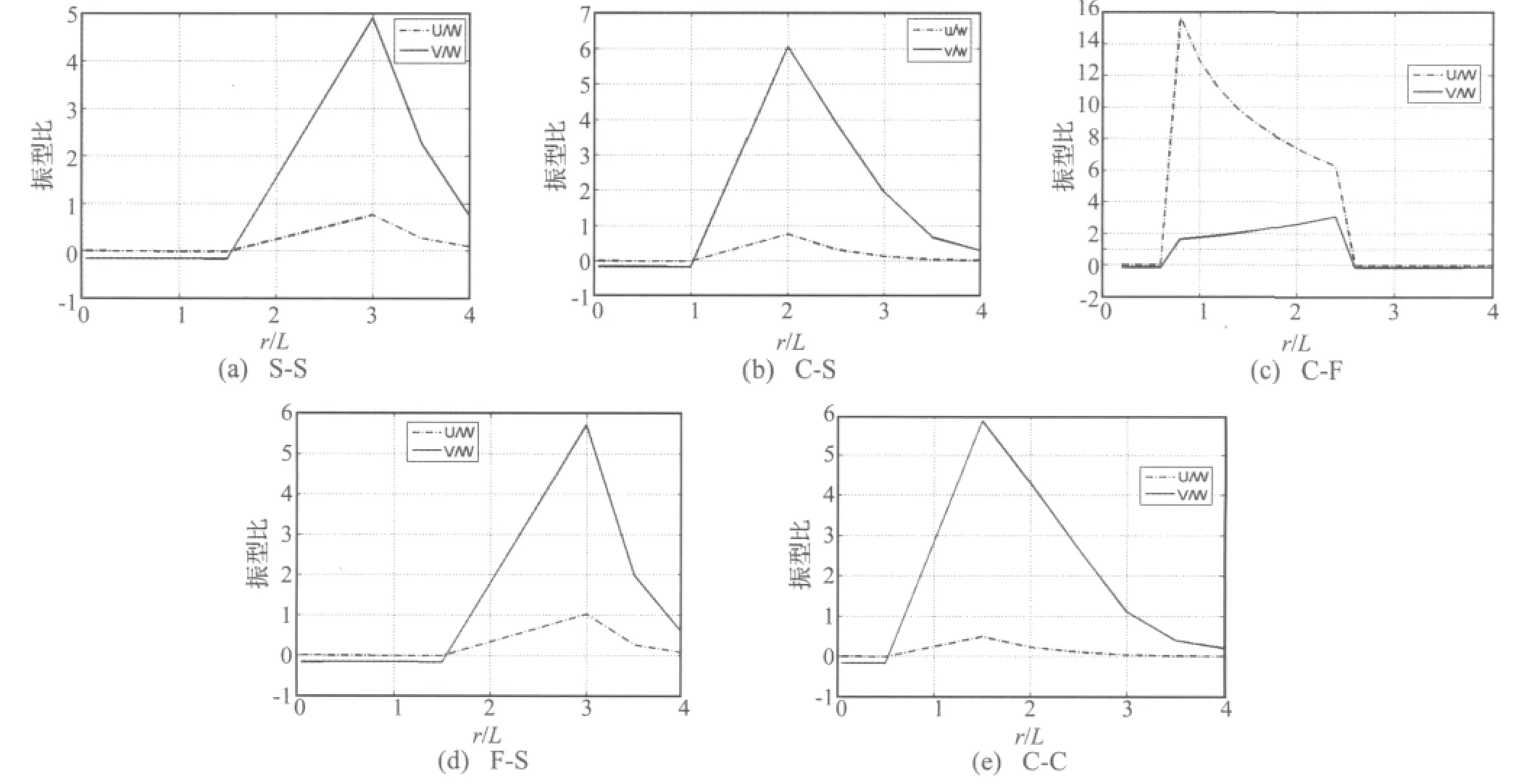
图7 圆柱壳的振型比Fig.7 Ratio of vibration mode for circular cylindrical shell

振型比为两个振动形态之比值，图7分别为简支－简支、固支－简支、固支－自由、自由－简支、固支－固支五种边界条件下圆柱壳的振型比图。由图可知，在给定的几种边界条件下，半径与长度之比r/L对圆柱壳系统振型比的影响显著;对于细长圆柱壳(r/L较小)，w方向振动最大，但对于短粗圆柱壳(r/L较大)，固支－自由圆柱壳u方向的振动最大，其它固支－简支，固支－自由，自由－简支，固支－固支四种边界情况均为v方向的振动最大。

3 结论

本文分析了几何参数厚度与半径之比h/r及半径与长度之比r/L对旋转薄壁圆柱壳固有频率与振型比的影响。结论如下:

(1)在给定的几种边界条件下，圆柱壳固有频率随着厚度与半径之比h/r的增加而单调增大，变化幅度较小。

(2)半径与长度之比对圆柱壳固有频率影响显著，且随着r/L的增大，频率值并不单调变化，在某范围内，系统的固有频率明显高于其它范围内的固有频率。

(3)r/L处于不同范围内时，不同边界简支－简支，固支－简支，固支－自由，自由－简支，固支－固支情况下，系统频率值的大小排序发生变化。其中，细长圆柱壳在固支－固支时频率最大，固支－自由时频率最小;相对较短的圆柱壳在自由－简支时频率最大。

(4)随着半径与长度之比的逐渐增大，当半径大于长度(r/L＞1)时，圆柱壳的固有频率明显高于半径小于长度(r/L＜1)时的固有频率。并且随着r/L的继续增大，圆柱壳固有频率值又开始减小。

(5)对于细长圆柱壳，应重点关注w方向振动;对于短粗圆柱壳应重点关注v方向或u方向的振动。细长圆柱壳的振动特性与短粗圆柱壳的振动特性差异显著。

［1］El-Mously M. Fundamentalnaturalfrequencies ofthin cylindrical shells:a comparative study［J］.Journal of Sound and Vibration，2003，264:1167－1186.

［2］杜长城，李映辉.功能梯度薄壁圆柱壳的自由振动［J］.动力学与控制学，2010，8(3):219－223.

［3］Li H，Lam K Y.Frequency characteristics of a thin rotating cylindrical shell using the generalized differential quadrature method［J］.International Journal of Mechanical Sciences，1998，40(5):443－459.

［4］Guo D，Chu F L，zheng Z C.The influence of rotation on vibration of a thick cylindrical shell［J］.Journal of Sound and Vibration，2001，242(3):487－505.

［5］Pradhana S C，Loya C T，Lama K Y，et al.Vibration characteristics of functionally graded cylindrical shells under various boundary conditions［J］.Applied Acoustics，2000，61:111－129.

［6］Gulgazaryan G R，Gulgazaryan L G，Saakyan R D.The vibrations of a thin elastic orthotropic circular cylindrical shell with free and hinged edges［J］. JournalofApplied Mathematics and Mechanics，2008，72:312－322.