反作用轮铰间隙对航天器动态特性影响分析

潘 冬，赵 阳，王兴贵，马文来

(哈尔滨工业大学 航天学院，哈尔滨 150001)

反作用轮是高精度航天器姿态控制的主要扰动源之一，随着航天事业的发展及哈勃望远镜、新一代望远镜(NGST)等一系列航天器的发射升空，预示着未来的航天器向高精度、高稳定性方向发展，目前中国在轨飞行的中低轨道遥感卫星成像精度与国际先进水平有明显差距，其主因即为飞轮扰动所致，对此迫切需要深入研究。

早在20世纪70年代，美国为解决反作用轮高频振动对哈勃望远镜成像精度的影响，对其使用的反作用轮扰动特性进行了深入研究。王全武［1］等提出了一种基于经验的飞轮扰动模型。Bialke［2］对反作用轮扰动的来源、实验与数学建模进行了全面的阐述。目前我国对飞轮扰动问题开展的研究集中在飞轮扰动理论模型建模技术主要考虑飞轮转子不平衡(静不平衡、动不平衡)、飞轮结构挠性、轴承振动与摩擦特性以及电机输出转矩特性等四方面［3－7］。未考虑飞轮转子与轴承间铰间隙的影响，运动副的存在间隙不可避免，运动副间隙主要由两种因素造成，一种由设计动配合生产加工形成的规则的原始装配间隙，一种由磨损引起的非规则的附加间隙，由于转子不平衡在旋转中发生偏心，且存在间隙，转子与轴套间发生接触碰撞产生的冲击，严重影响航天器的控制精度与稳定性。

本文以某高指向要求的遥感观测卫星为例，基于虚拟样机技术，引入间隙矢量模型，对铰间隙进行建模，通过对Adams中已有模型参数的设定及自定义模型的引入，得到考虑飞轮铰间隙的卫星系统虚拟样机模型，分析其反作用轮铰间隙对卫星系统动态特性的影响，进而为控制系统的设计与优化提供参考。

1 反作用轮间隙铰动力学建模

反作用轮是卫星姿控系统关键执行部件，主要由支撑轴、轴承、飞轮转子、驱动电机等零部件组成［8］，驱动电机输出力矩使飞轮转子高速旋转，从而提供卫星进行姿态机动或保持的力矩。飞轮转子与轴承间存在间隙，由于飞轮转子的动不平衡，转子与轴承间发生接触碰撞，随着运行时间的变长将产生磨损，加大间隙，间隙的变大又会导致碰撞冲击剧烈进一步磨损，这是个循环促进的过程，研究铰间隙对机构动态特性影响，其关键是对铰间隙进行正确描述。

1.1 间隙铰矢量模型

运动副铰间间隙的存在对机构主要有两方面的影响:首先，由于间隙的存在，系统成为拓扑结构可变的系统。含间隙的系统具有两种拓扑结构:一种是两体之间在间隙的方向上失去铰间约束，构件体做自由运动;另一种是两体之间相互接触，构件体做具有单边约束的运动。间隙的另一个影响是机构在运动中产生内碰撞，含间隙的变结构系统总是在自由运动和单边约束两种状态间相互切换，而这种状态间的切换几乎不可能是光滑、平稳的，总要包含一定的碰撞，而碰撞即会产生碰撞力，从而影响机构的稳定性。

对卫星反作用轮系统铰间隙的真实有效描述是实现卫星系统运动、动力学仿真的关键。本文主要定性研究反作用轮铰间隙对卫星系统的影响，将轴承考虑成轴套，不考虑轴承的复杂结构。如图1所示，间隙矢量模型通过在转子轴和轴套的旋转铰中引入一个间隙矢量来表达旋转铰的真实潜在行为，间隙矢量表征轴和轴套两构件间连接点的精确相对位置。

间隙矢量定义在一个局部浮动笛卡尔坐标系中，以轴套的回转中心为间隙矢量的基准起始点，间隙矢量的方向指向轴和轴套相对运动时的潜在接触点，该潜在接触点构成了轴与轴套的相对碰撞点对。间隙矢量的大小被严格限制在以轴套回转中心为圆心且以轴和轴套的径向尺寸公差为半径的间隙圆内，间隙矢量大小的变化能反映间隙运动副元素是否接触［9］。

图1 运动副间隙矢量模型Fig.1 Sketch of revolute joints with clearance

对含间隙反作用轮系统，假设转动副铰接处轴套与轴同心，间隙大小用轴套与轴半径之差表示，则间隙为:

式中:ri为轴套半径，rj为转子轴半径，eij为间隙矢量。

1.2 间隙铰数学模型

图2为轴与轴套碰撞时旋转铰间隙示意图，Oi和Oj分别为轴承和轴的中心和是轴套和轴的中心在全局惯性坐标系下位置矢量。

由图2可知，轴套与轴的间隙矢量为:

根据间隙矢量定义知，间隙矢量表示轴相对于轴套的偏心矢量。轴与轴套碰撞时的法线单位矢量表示为:

Qi和Qj分别为轴套和轴的潜在接触点，和是轴套和轴潜在接触点对在全局惯性坐标系下的位置矢量，当轴套和轴接触碰撞时，碰撞引起接触变形的大小表示为:

其中:c为初始间隙，是轴套与轴的半径之差，由式(1)求得。因此接触变形量与间隙矢量相关。

图2 碰撞时旋转铰间隙示意图Fig.2 Bump of revolute joints with clearance

轴与轴套是否发生碰撞可根据接触变形量δ判定，轴与轴套接触碰撞条件为:

在轴与轴套发生接触碰撞时，会产生接触碰撞力，为计算碰撞力大小，需知道轴与轴套碰撞时接触面间法向相对速度及切向相对速度，将δ·向碰撞接触平面投影即可得到:

法向单位矢量n的方向可根据式(3)求得，切向单位矢量t的方向可由n逆时针旋转90°得到。

1.3 间隙铰接触碰撞力模型

间隙铰的一个重要特征就是其系统为变拓扑系统，即分为无约束的自由运动和受单边几何约束的运动，自由运动时机构在运动副处不受力的作用较好处理，但是当受单边几何约束时，运动副处将会有力的作用，为了建立系统动力学模型，需要将几何约束转化为力约束，利用合理的碰撞力模型来预测接触碰撞力将是建立正确动力学模型的关键。

本文采用非线性弹簧阻尼模型建立轴与轴套间隙接触碰撞模型［10－11］，如图3所示其广义形式表示为:

式中:Fn为接触点法向接触力;Kn为等效接触刚度;δ为接触点法向穿透深度为接触点法向相对速度;C(δ)为与δ有关的阻尼因子;m为指数，m≥1。弹簧恢复力Fk由Hertz接触理论确定:

为克服线性阻尼模型接触初始时刻碰撞力不为零的局限性，采用非线性阻尼模型确定接触碰撞过程中的阻尼力Fd:

其中:C为阻尼系数，与恢复系数及接触刚度有关:

等效接触刚度Kn取决于两个接触碰撞体的几何特征及材料属性，根据Hertz接触理论可知:

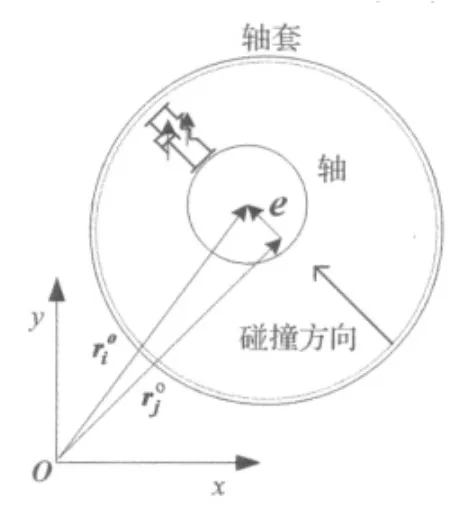
图3 旋转铰非线性弹簧阻尼模型Fig.3 Nonlinear equivalent spring-damp model

其中:ν，E分别为泊松比与杨氏模量。

1.4 间隙铰摩擦力模型

反作用轮转子与轴套间还存在切向摩擦力，其力矩会进一步影响含间隙机构的动力学特性，求解间隙处切向摩擦力采用修正的Coulomb摩擦模型［12］，切向摩擦力表示为:

其中:μd为滑动摩擦系数，cd为动态修正系数，νt为相对切向速度。cd由下式获得:

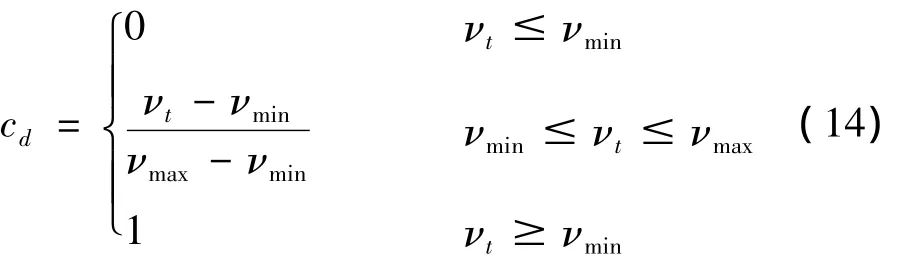
式中:νmin，νmax为给定的速度极限值。

通过建立的法向接触力与切向摩擦力模型，可较准确描述反作用轮系统间隙铰处的约束问题，从而根据多体动力学理论得到考虑反作用轮铰间隙的卫星系统动力学方程。

引入阶跃函数:

间隙处约束力为:

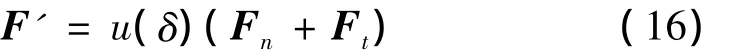
从而含间隙双轴驱动机构动力学方程为:

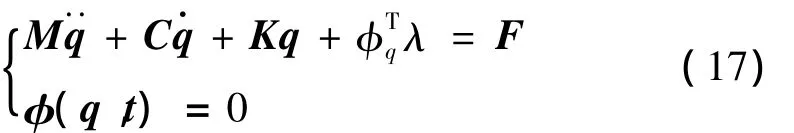
式中:q为广义坐标列阵，M，C，K，φq，F分别为卫星系统的广义质量阵、阻尼阵、刚度阵、约束方程的雅克比矩阵、广义速度二次项以及力阵的和，λ为Lagrange乘子列阵。

2 虚拟样机模型

对于含间隙机构动力学问题，准确检测接触碰撞点并精确求解是研究的难点问题。当建立了机构的动力学模型后，如何编程实现对接触碰撞点的实时检测将很困难，而多体动力学分析软件Adams能很好的解决这一问题，所以本文基于虚拟样机技术，应用Adams计算平台对考虑反作用轮铰间隙的卫星系统进行仿真分析。

卫星的整星结构包括推进舱、服务舱、有效载荷舱以及太阳帆板、连接架、服务舱隔板等。其中在服务舱中装有反作用轮系统，本文主要研究反作用轮转子与轴套间隙对卫星系统动态特性的影响，所以在太阳帆板、连接架等结构与卫星本体间定义固定副，作为一个整体，不计太阳帆板柔性的影响。为考虑飞轮转子不平衡因素的影响，在转子上加一较小的附加质量，如图4所示。

图4 反作用轮不平衡示意图Fig.4 Reaction wheel unbalanced

通过建立的反作用轮间隙处动力学模型，用间隙铰处接触碰撞产生的力约束代替含间隙的几何约束，从而达到考虑铰间隙进行动力学仿真的目的，图5为建立的卫星系统虚拟样机模型。

图5 卫星系统虚拟样机Fig.5 Virtual prototype model of satellite

3 仿真结果与分析

间隙铰的存在，对卫星系统的动态特性及指向精度都将产生一定的影响，基于建立的虚拟样机，分别针对飞轮转子与轴套间为理想铰及间隙铰两种情况进行仿真分析，分析铰间隙对各特征变量的影响。

3.1 仿真条件

航天器材料为铝蜂窝夹层板结构，在进行仿真运算时，对其结构特性进行假设等效，仿真中的结构参数如表1所示。反作用轮转子半径rj=0.0195 m，轴套半径为ri=0.02 m。半径间隙c=0.0005 m，电机输出力矩为M1=0.1 Nm，间隙接触等效刚度值为1.3×108N/m、等效阻尼值为176 Ns/m，滑动摩擦系数为0.1。

表1 卫星系统结构参数Tab.1 Structure parameters of the satellite

3.2 结果分析

根据以上仿真条件，对卫星系统虚拟样机进行仿真分析，结果如图6所示。

图6 间隙矢量距Fig.6 Sketch of revolute joints with clearance

图6为反作用轮转子与轴套的间隙矢量距，根据间隙矢量定义知，初始时转子与轴套同心，间隙矢量距为0，当电机对转子施加转矩后，转子转动并发生偏心，与轴套接触碰撞，轴套与转子间隙为0.5mm，当间隙矢量距达到0.5mm时即代表发生接触，从图中可看出只是在运动初期转子与轴套有脱离接触，随着转子转速的增加，两者一直保持接触状态，即运动副间发生连续接触变形。

图7 卫星系统平动特性Fig.7 Translational characteristics of satellite systems

图8 卫星系统转动特性Fig.8 Rotational characteristics of satellite systems

图7为卫星本体在反作用轮作用下，理想铰与间隙铰两种不同工况下质心的平动特性，其中图7(a)为质心的位移曲线，由于间隙的存在，使卫星在姿态机动过程中位置出现偏差，且随着时间的积累偏差逐渐增大。从图7(b)、图8(a)卫星的平动速度、角速度曲线中看出，间隙使卫星速度发生波动，而间隙处消耗能量，在电机输出转矩相同情况下，考虑间隙时卫星的机动速度小于理想情况下的速度。图7(c)、图8(b)卫星的加速度曲线表明，间隙使间隙铰处发生内碰撞，加速度出现很大的峰值。

通过分析可知，由于反作用轮转子与轴套间存在的间隙，使卫星系统的速度与加速度都出现很大的波动，对于系统的稳定性及定位精度极其不利。

图9为卫星反作用轮系统间隙铰处产生的接触碰撞力，其中图9(a)、图9(b)分别为法向接触力和切向摩擦力，由动力学建模过程可知，法向接触力由弹簧阻尼器等效求得，而摩擦力则根据修正的库伦摩擦力模型求得。从图中可看出，由于间隙的存在，间隙铰处发生内碰撞，法向力和摩擦力都有很大的冲击峰值，且法向力数值大于摩擦力，图9(c)为接触碰撞力的合力与理想铰铰间力的对比，从图中明显看出考虑间隙情况下的接触碰撞力远大于理想情况下产生的铰间力，最大峰值约为理想情况下的10倍，过大的冲击力将加速机构的破坏与磨损，反作用轮铰间隙的存在对于卫星系统的定位精度及工作寿命影响极大。

图9 间隙接触碰撞力Fig.9 Joint clearance bump force

4 结论

反作用轮作为卫星姿态控制系统的关键执行部件，其也是影响高精度航天器的主要扰动源之一，文中采用非线性弹簧阻尼模型建立了间隙处的接触碰撞模型，同时采用修正的Coulomb摩擦模型考虑运动副间隙处的摩擦作用，研究了反作用轮铰间间隙对卫星系统动态特性的影响。仿真结果表明:

(1)反作用轮铰间隙的存在，将影响卫星系统的定位精度，出现定位偏差，且随着运行时间的增长，偏差累积增大。

(2)间隙的存在使铰间发生内碰撞，引起卫星系统速度、加速度剧烈抖动，产生很大的峰值。

(3)铰间的内碰撞将产生很大的接触碰撞力，加速机构的磨损与破坏，影响反作用轮系统的使用寿命。运动副间隙不可避免，在建立反作用轮系统扰动模型时应充分考虑间隙对系统的影响，以获得更准确的扰动模型，为航天器材料的选择及控制系统设计提供参考。

［1］王全武，虎 刚.飞轮扰动原因与测量技术现状［J］.空间科学学报，2009，29(1):39 －44.

［2］Bialke B.A compilation of reaction wheel induced spacecraft disturbances［C］.Proceedings of the 20th Annual AAS Guidance and Control Conference，AAS，1997:97 －038.

［3］孙 杰，赵 阳，王本利.航天器反作用轮扰动精细模型［J］.哈尔滨工业大学学报，2006，38(4):520 －522.

［4］张鹏飞，程 伟，王 和.航天器反作用轮扰动建模及参数辨识［J］.北京航空航天大学学报，2010，36(7):879－882.

［5］李连军，戴金海.反作用轮系统内干扰建模与仿真分析［J］.系统仿真学报，2005，17(8):1855 －1863.

［6］庞世伟，杨 雷，曲广吉.高精度航天器微震动建模与评估技术最近进展［J］.强度与环境，2007，34(6):1 －9.

［7］孙 杰，赵 阳，田 浩.改善航天器反作用轮扰动实验模型参数辨识方法［J］.空间科学学报，2006，26(1):70－74.

［8］白争锋，赵 阳，马文来.反作用轮扰动对航天器结构动态特性的影响分析［J］.宇航学报，2009，30(5):2073－2079.

［9］时 兵，金 烨.面向虚拟样机的机构间隙旋转铰建模与动力学仿真［J］.机械工程学报，2009，45(4):299 －303.

［10］Dubowsky S， Freudenstein F. Dynamic Analysis of Mechanical Systems with Clearances，Part 2:Dynamic Response［J］.Trans.ASME.Eng.Ind.，1971，93(1):310－316.

［11］Flores P.Dynamic analysis of mechanical systems with imperfect kinematic joints［J］.Universidade Do Minho PhD thesis，2004:50 －62.

［12］Flores P J.Modeling and simulation of wear in revolute clearance joints in multibody systems［J］.Mechanism and Machine Theory，2009，44:1211－1222.