飞机垂尾抖振极限载荷预测方法

杨智春，陈 帅，金 伟

(1.西北工业大学 航空学院结构动力学与控制研究所，西安 710072;2.成都飞机设计研究所 强度部，成都 610041)

飞机垂尾抖振是典型的气动弹性耦合效应下随机振动问题。以美国 F/A －22［1－2］和 F/A －18 飞机［3－6］为代表的许多双垂尾布局的先进战斗机，在大攻角飞行时承受着严重的抖振载荷，研究发现这正是引起垂尾结构部件疲劳损伤的根源之一［7］，因而在高性能战斗机设计中，垂尾抖振备受关注。虽已有研究表明，垂尾抖振产生的根源在于飞机设计时采用的机翼前缘大边条与双垂尾布局，但是无论是采用被动的抖振减缓措施［8－9］或主动的抖振控制方法［10－11］，都不能完全抑制抖振载荷。因此，垂尾抖振极限载荷的预测结果，为相关部件结构设计与强度校核提供了重要依据。

由于对先进战斗机高速、大机动飞行性能的要求，在该类飞机全包线范围内出现抖振不可避免;因此，当考虑抖振载荷影响时(特别是对于某些抖振效应明显的飞行状态)，飞机强度估算与校核中均须在原有静载荷基础上叠加上飞机抖振载荷的影响成分，以保证飞机结构在全包线飞行中具有足够的强度。然而，在进行极限载荷预测时，若单纯由最大机动载荷与最大抖振载荷叠加获取抖振飞行状态的极限载荷值，将使设计过于保守，不能充分利用结构性能;若忽略抖振载荷，则会使设计过于冒险因而招致非常严重的后果。此外，抖振载荷的测点数目不足及载荷测试类型有限等也会给抖振极限载荷预测带来困难。为解决这些问题，本文首先对可能出现垂尾抖振飞机飞行状态进行子状态划分，然后对抖振载荷进行重构，以解决实际工程中抖振载荷的测点数目不足与载荷测试类型有限等问题，最后基于建立的抖振飞行子状态载荷概率分布模型，建立飞机垂尾抖振极限载荷的预测方法，以给出恰当的极限载荷结果。

1 飞机垂尾抖振飞行子状态划分

由于飞机垂尾抖振载荷是一种随机激励载荷，且这种载荷与飞机的飞行状态密切相关，因此可将飞机垂尾出现抖振的包线范围按照相关飞行状态参数划分为若干子状态，并假设各飞行子状态内抖振载荷满足相同的概率分布规律。

通常抖振飞行子状态按飞机飞行的攻角α、动压q、马赫数M及侧滑角 β进行划分［1］，具体步骤如图1所示:先分别将可能出现抖振的攻角范围、动压范围、马赫数范围及侧滑角范围分为若干子区间;后将不同的攻角、动压、马赫数及侧滑角子区间进行组合;再根据对任务剖面的分析，剔除不可能出现的飞行子状态及不可能出现垂尾抖振的飞行子状态，最后采用四维量B(i，j，m，n)对各抖振飞行子状态载荷数据进行存储定位(i为攻角子区间标号，j为动压子区间标号，m为马赫数子区间标号，n为侧滑角子区间标号)，以此建立抖振载荷数据库的数据存储关系。

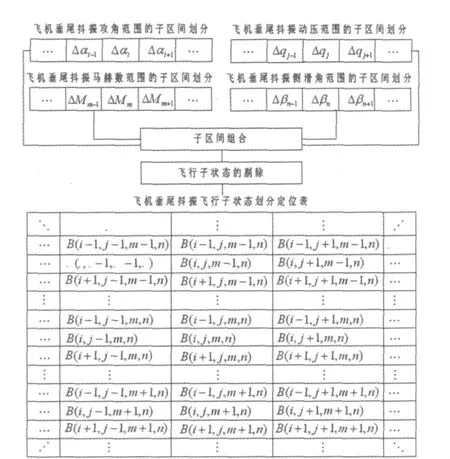
图1 飞机垂尾抖振的飞行子状态划分Fig.1 Flight subcase split of aircraft vertical tail buffeting

2 抖振极限载荷预测方法

2.1 基于有限测试响应的抖振载荷重构

抖振载荷数据的获取途径主要有两种:① 有限元仿真计算，② 试验测试。在初始设计阶段，一般由有限元仿真计算抖振载荷数据，通过这种途径获得的载荷具有信息较完整的优点，因此只需要分析结构上同一位置在不同抖振飞行子状态下的临界载荷，进而得到该位置的抖振极限载荷，其它位置依此类推;然而，在试验校核阶段需要通过测试获得相应的数据，由于测试条件的限制，测试位置十分有限，需要根据测试位置的载荷识别(重构)未测位置的载荷，然后按照同样方法进行考虑抖振因素的极限载荷预测。

通常抖振响应测试得到的是加速度，而加速度响应从物理坐标向模态坐标的转换关系为:

通常，处理后的［Φ］并非方阵，故由广义逆求解得保留的模态加速度向量{}为:

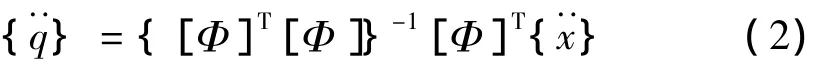
有限元方法中，响应可用节点位移通过变换获取，故首先由数值积分求得保留模态速度向量为:

再次积分，可求得保留模态位移响应为:

考虑到积分时速度与位移初值无法直接确定，则由式(3)与式(4)得到的为通解，故需要增加约束条件才能得到{}与{q}的定解。在此利用加速度、速度和位移间的相位关系进行约束，具体为:①模态加速度峰值时的零模态速度约束，②模态速度峰值时的零模态位移约束。

最后，由模态叠加原理得:

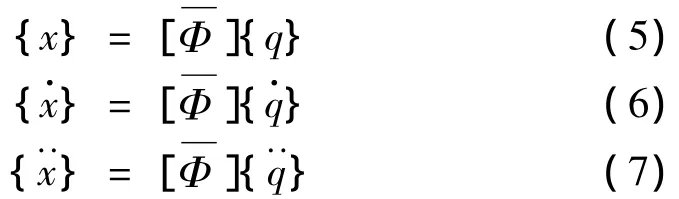
由有限元法中，节点位移{x}与应变{ε}或应力{σ}之间转换关系可得:

其中，［B］为几何矩阵，［D］为弹性矩阵，［S］为应力矩阵。由单元形函数即可求得所需内载荷。

同时将响应代入其运动基本方程还能得外激励载荷 {f}为:

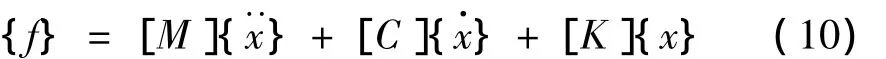
其中，［M］，［C］和［K］分别为结构的质量矩阵、阻尼矩阵与刚度矩阵。

按照图2所示流程，就可用有限测点处的抖振响应重构出飞机垂尾结构的抖振载荷，包括内载荷(动响应，即位移、速度、加速度、应变和应力)及外载荷(即外激励载荷)。

2.2 抖振飞行子状态载荷概率模型

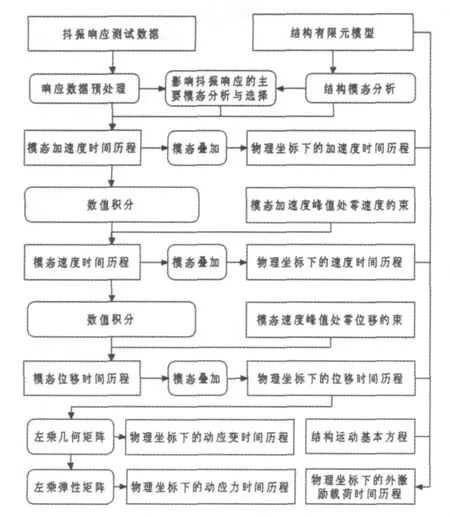
图2 抖振载荷的重构Fig.2 Reconstruction of buffet loads

考虑到飞机垂尾抖振载荷的随机性，通常需要利用统计方法建立抖振载荷的概率模型以降低分散性，并进行抖振极限载荷估算。因此统计变量并非各时刻对应的载荷值，而应选择载荷峰谷值进行统计。

选去均值处理后的抖振飞行子状态下的载荷峰值谷值绝对值Y与该状态下抖振载荷均方根RMS的比值作为无量纲化的统计量Z［12］，即:

选择合适的飞机垂尾抖振载荷概率分布假设［13］，即可建立合适的反映抖振载荷峰谷值特性的概率分布模型，且可通过概率分布参数的最大似然估计，确定相应假设下统计量Z超过某一给定临界值ZcrB时的概率:

该概率值由下式得到:

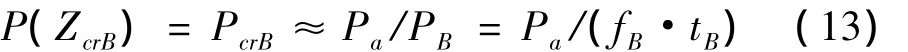
其中，Pa为飞机设计中按要求给出的全寿命内可接受超过设定抖振载荷次数［1］，P(ZcrB)(即PcrB)为某抖振飞行子状态下抖振载荷超过给定值概率，PB为全寿命内该抖振飞行子状态载荷总循环次数，fB和tB分别为通过飞行任务剖面分析给出的全寿命内该抖振飞行子状态载荷循环频率及其出现的总时间。

联立式(12)和式(13)，得:

其中，P－1表示函数P(Z)的反函数，YcrB为该抖振飞行子状态对应的临界抖振载荷绝对值。

2.3 抖振飞行子状态临界载荷确定

按照叠加原理合成各节点总载荷，即:

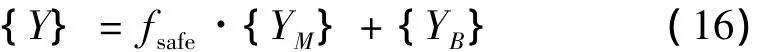
其中:{Y}为节点总载荷向量;{YM}为节点机动载荷向量;{YB}为节点抖振载荷向量;fsafe为安全系数，一般取fsafe=1.5。注意，此处的载荷既可以是内载荷(动响应，即位移、速度、加速度、应变和应力)，又可以是外载荷(即外激励载荷)。

为确定抖振极限载荷，将式(15)得到的各子状态抖振临界载荷向量代入式(16)，得到穿越线上下临界载荷为:

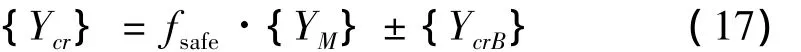
由于不同状态下不同位置的机动载荷向量{YM}与临界抖振载荷向量{YcrB}的相对大小及方向各不相同，因此，每个节点上可由式(17)计算得到两个临界载荷Ycr，该临界载荷中，较大者为上临界载荷，较小者为下临界载荷。由此可得到各节点上抖振飞行子状态穿越线上下临界载荷。

2.4 抖振极限载荷确定

取第k个节点上所有抖振子状态穿越线临界载荷Ycr所组成的临界载荷集合{Ycr}k中最小元素与最大元素，即:

则第k个节点抖振极限载荷Yultimate，k满足:

第1步：根据组别T分层，分别对Y（成功与否）做Logistic回归，得到两个Logistic模型。即当T=1时得到模型A，当T=0时得到模型B。

考虑抖振影响的节点载荷Yk满足:

其它节点的处理与此相同，不再赘述。

3 应用实例分析

某型飞机在给定抖振飞行子状态下某节点抖振载荷(已无量纲化)时间历程数据如图3所示。

飞机垂尾抖振载荷概率分布假设选择威布尔分布［13］，为满足此飞行状态下该节点抖振载荷时程数据的处理要求，由参数的最大似然估计得统计量Z超过某一给定临界值 ZcrB时的概率为［12－13］:

图3 某型飞机在给定子状态下某节点抖振载荷时间历程Fig.3 Nodal load time history of buffet at a given subcase

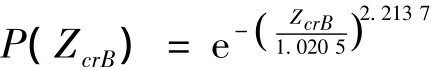
则:

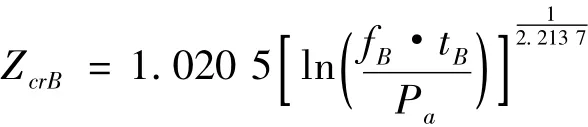
进而:

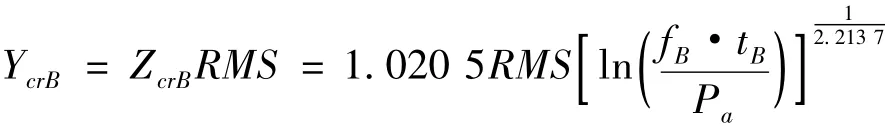
通常，飞机全寿命范围内可接受的穿越次数取Pa=1 ×10－4次［1］，载荷均方根为 RMS=0.3840，且 PB=fB·tB=165240次，则此飞行状态下该节点的临界抖振载荷YcrB=1.5579。机动载荷YM=21，则其穿越线上下临界载荷为:

类似地，可得到所选临界载荷状态该节点的穿越线临界载荷Ycr，如表1所示。

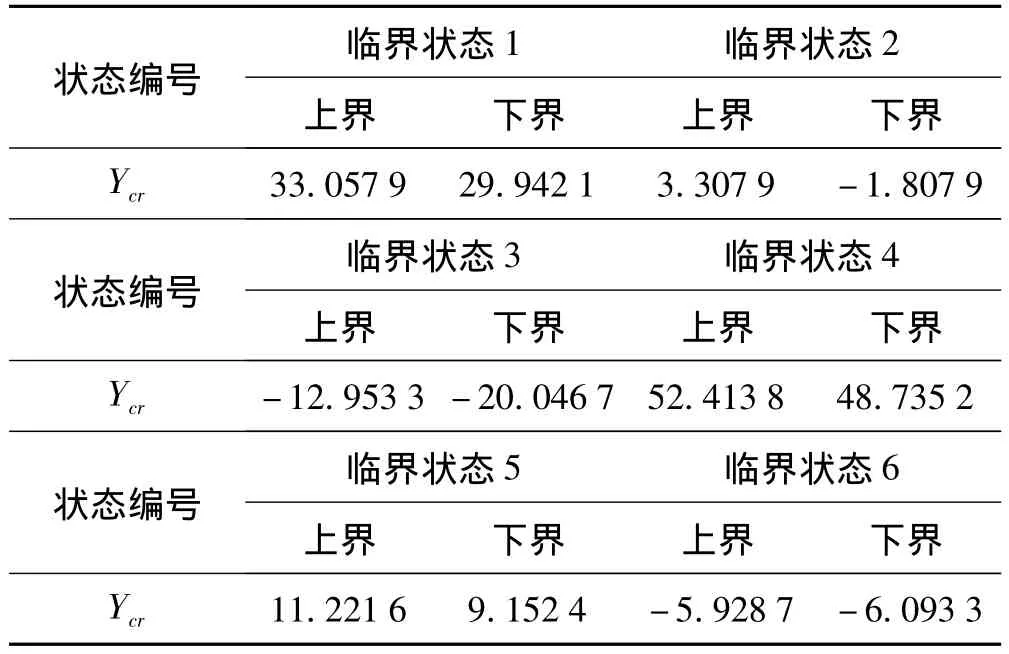
表1 某节点的抖振临界载荷Tab.1 Critical buffet loads at a given node

因此，该节点上所有抖振飞行子状态穿越线临界载荷Ycr组成的临界载荷集合{Ycr}k为:

显然，其极限载荷为:

抖振载荷作用时，第k个节点的载荷范围满足:

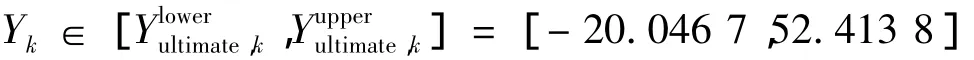
采用同样的方法，可获得不同节点上的极限载荷，进而为结构强度校核提供载荷依据。

4 结论

为满足先进战斗机高速、大机动飞行性能的要求，在飞机设计的强度估算与校核中必须考虑抖振载荷影响，以保证飞机结构在全包线飞行中具有足够的结构强度，本文提出的飞机垂尾抖振极限载荷预测方法，具有如下特点:

(1)提出的抖振载荷重构方法，可有效地解决实际工程中抖振载荷的测点数目不足与载荷测试类型有限等问题，其重构载荷类型既可以是内载荷(动响应，即位移、速度、加速度、应变和应力)，又可以是外载荷(即外激励载荷)，满足了不同的应用需求。

(2)由于飞机垂尾的抖振载荷规律随其飞行状态的变化而改变，且各飞行状态在全寿命中出现的比例不尽相同，因此在抖振飞行子状态划分后，对子状态内数据统计规律的分析结果，便于结合飞行剖面分析而应用于后续的抖振疲劳寿命估算与疲劳载荷谱编制，便于建立抖振载荷数据库中数据的存储关系，有利于数据分类存储与搜索定位。

(3)根据不同抖振飞行子状态下相应机动载荷与抖振载荷叠加组合的最值情况(即两者方向相同与相反的情况)筛选抖振极限载荷，既避免了由单纯采用最大机动载荷与最大抖振载荷叠加所获取的抖振极限载荷值过于保守的问题，又解决了忽略抖振载荷所确定的极限载荷值过于冒险的问题。

［1］Patel S R，Black C L，Anderson W A，et al.F/A －22 vertical tail buffet strength certification［C］.AIAA－ 2005－2292， 46th AIAA/ASME/ASCE/AHS/ASC Structures，StructuralDynamics ＆ Materials Conference， Austin，Texas，2005.

［2］Patel S R，Black C L.Statistical modeling of F/A－22 flight test buffet data for probabilistic analysis［C］.46th AIAA/ASME/ASCE/AHS/ASC Structures，Structural Dynamics ＆Materials Conference，2005.

［3］Zimmerman N H，Ferman M A.Prediction of tail buffet loads for design application［J］.Vols.I and II，Naval Air Development Center NADC－88043－60，1987.

［4］Ferman M A，Patel S R，Zimmerman N H，et al.A unified approach to buffet response of fighter aircraft empennage［R］.Aircraft Dynamics Loads due to Flow Separation，AGARD Report CP－ 483， North AtlanticTreatyOrganization，Sorrento，Italy，September，1990.

［5］Triplett W E.Pressure measurements on twin vertical tails in buffeting flows［R］.AFWAL Report AFFDL TR－82－3015，1981.

［6］Shah G H，Grafton S B，Guynn M D，et al.Effect of vortex flow characteristics on tail buffet and high angle of attack aerodynamics of a twin tail fighter configuration［C］.High Angle of Attack Technology Conference，1990.

［7］Lee B H K.Vertical tail buffeting of fighter aircraft［J］.Progress in Aerospace Sciences，2000，36:193 －279.

［8］Sheta E F.Alleviation of vertical tail buffeting of F/A－18 aircraft［J］.Journal of Aircraft，2004，41(2):322 － 330.

［9］Sheta E F，Huttsell L J.Numerical analysis of F/A －18 vertical Tail［C］.AIAA 2001 － 1664.42nd AIAA/ASME/ASCE/AHS/ASC Structures，Structural Dynamics ＆Materials Conference Seattle，WA － April 16 －19，2001.

［10］Sheta E F，Moses R W，Huttsell L J，et al.Active control ofF/A－18 vertical tail buffeting using piezoelectric actuators［C］.AIAA 2003－1887，44th AIAA/ASME/ASCE/AHS Structures，Structural Dynamics ＆ Materials Conference，Norfolk，Virginia，2003.

［11］Roberts P，Yang B J，Hanagud S，et al.Adaptive control of F/A －18 vertical tail buffeting［C］.AIAA 2006 －6345，AIAA Guidance，Navigation，and Control Conference and Exhibit，Keystone，Colorado，2006.

［12］陈 帅，杨智春，李 斌.飞机抖振响应数据处理与分析方法［J］.振动与冲击，2011，30(6):15－19.

［13］杨智春，陈 帅，李 斌.基于统计与粗糙集理论的飞机垂尾抖振载荷分布假设选择与评价方法［J］.振动与冲击，2012，31(5):6－11.