随机风场中覆冰四分裂导线舞动数值模拟

刘小会，严 波，张宏雁，周 松

(1.重庆大学 工程力学系，重庆 400030;2.四川电力科学研究院，成都 610071;3.四川省电力工业调整试验所，成都 610016)

覆冰导线舞动对高压输电线路安全和可靠运行构成严重威胁。对其研究具有极其重要的理论意义和工程实用价值。目前国际上普遍接受的有Hartog［1］垂直舞动理论和Nigol［2］扭转舞动理论及惯性耦合机理和稳定性机理等。随着计算力学的发展，数值模拟方法已成为研究覆冰导线舞动的重要手段。研究对象从覆冰单导线的舞动到覆冰多分裂导线的舞动，研究方法从采用线性化的振型叠加法到考虑大位移的几何非线性方法，已有不少研究成果。Desai等［3］提出了一种具有扭转自由度的索单元模拟覆冰导线，采用有限元方法研究覆冰单导线的舞动，但在求解运动方程时采用了振型叠加技术，进行了线性化处理。Angelo等［4－5］采用曲梁单元模拟覆冰导线，研究了覆冰单导线的舞动。Zhang等［6］通过建立混合模型，将分裂导线等效为一根特征线，研究了分裂导线的舞动。何锃等［7］提出了模拟分裂导线的三维有限元模型，在模型中考虑了防振锤。但这些研究均未考虑作用于分裂导线各子导线上空气动力载荷的不同。严波等［8－9］在文献［6］的基础上给出了覆冰双分裂导线和四分裂导线舞动的数值模拟方法，考虑了由于尾流效应引起各子导线不同的空气动力载荷，并讨论了由于各子导线气动参数的不同，多分裂导线与单导线舞动特性存在的差异。Liu等［10］研究了覆冰单导线舞动非线性有限元方法，通过数值模拟发现了一种可能的新型舞动模式。在此基础上给出了模拟覆冰分裂导线舞动的非线性有限元方法［11］。

高压输电线路的档距和弧垂一般较大，研究输电线路在风激励下的响应问题时，须要考虑风场的随机性［12］。本文采用数值方法模拟随机风荷载作用下覆冰导线的舞动特征，为进一步防舞研究奠定基础。

1 覆冰导线空气动力特性试验结果

在中国空气动力研究与发展中心1.4 m×1.4 m低速风洞中完成了典型新月形和扇形覆冰四分裂导线的空气动力系数风洞试验，详细的试验方法和过程参见文献［13］。在此仅考虑12mm厚新月形覆冰情况，图1所示为新月形覆冰四分裂导线现场照片和简化模型。

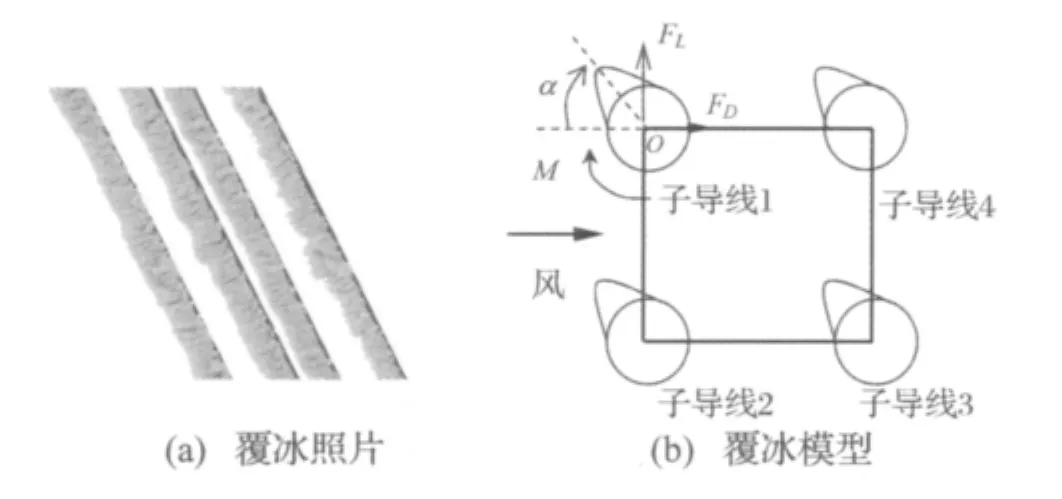
图1 新月形覆冰模型Fig.1 Crescent-shaped ice model

覆冰子导线的阻力系数、升力系数和扭矩系数可分别定义为:

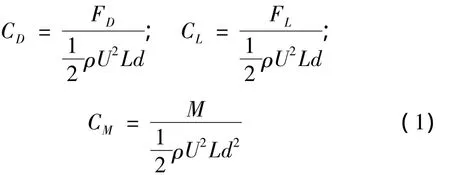
式中:FD，FL，M分别为覆冰导线所受阻力、升力和扭矩;ρ为试验环境温度下空气密度;U为风速;L为导线模型有效长度;d为导线直径。

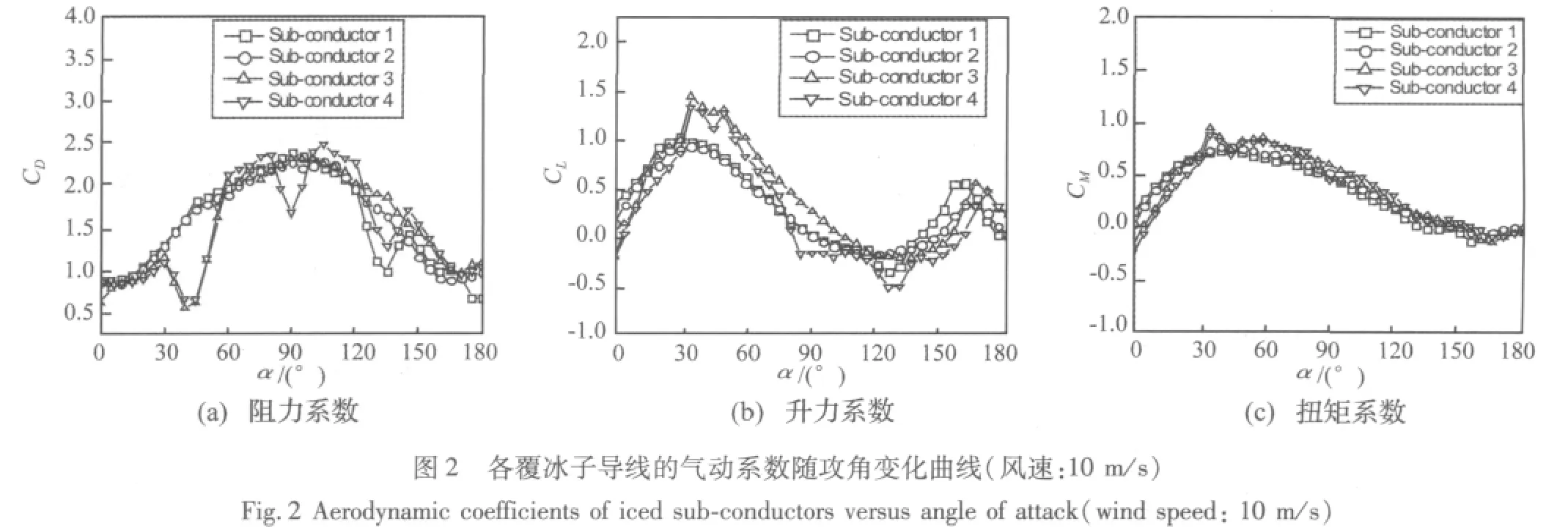
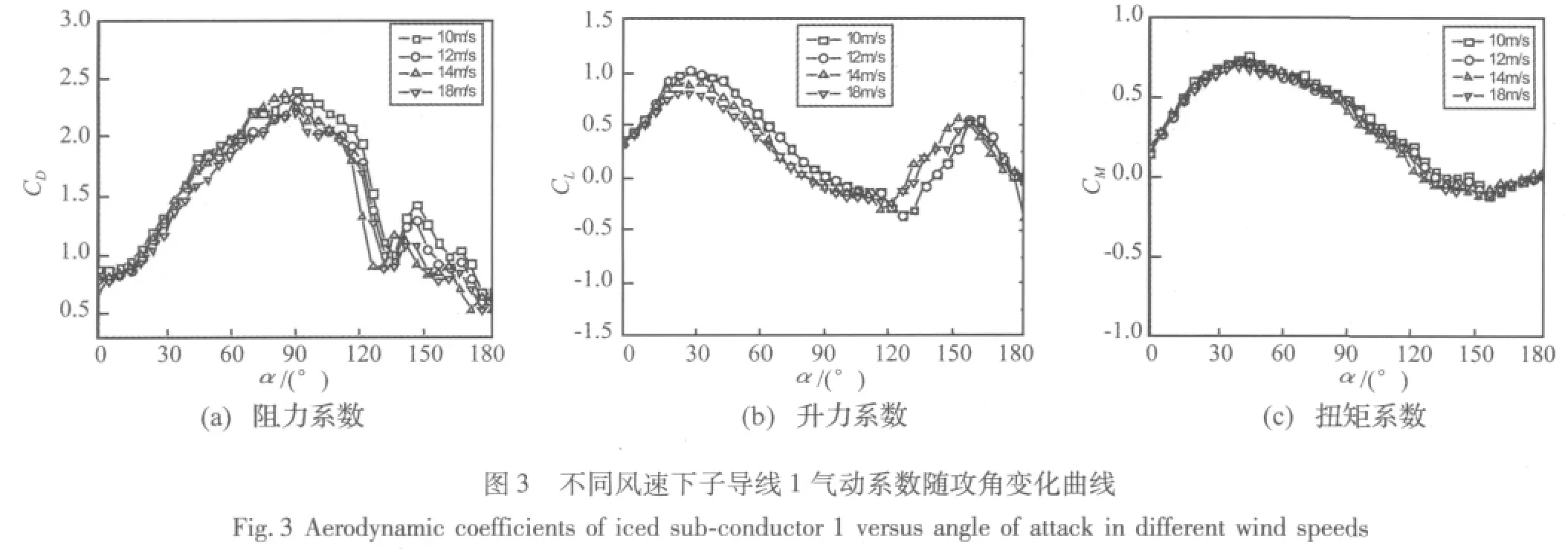
图2所示为厚度为12mm的新月形覆冰四分裂导线在10 m/s风速下空气动力系数随风攻角的变化曲线。由于子导线尾流的影响，四根子导线的空气动力系数存在差异。试验结果表明，在舞动发生的风速范围内风速对覆冰导线气动系数的影响很小［13］，图3所示为12mm厚新月形覆冰四分裂导线子导线1在不同风速下空气动力系数随风攻角的变化曲线。

2 空间变化随机风场数值模拟方法

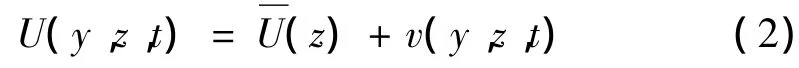
式中:a为地面粗糙度系数，与地貌有关。

各国学者提出了多种脉动风速功率谱，工程中常采用考虑随高度变化的Kaimal谱［14］为:

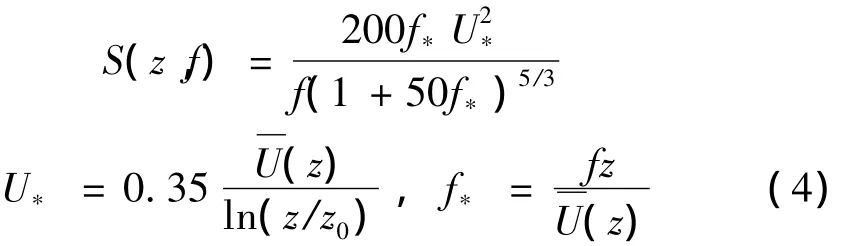
式中:U*为剪切速度;z0为地面粗糙长度，f为频率，z为离地高度。

脉动风速互相干谱可写成［14］:

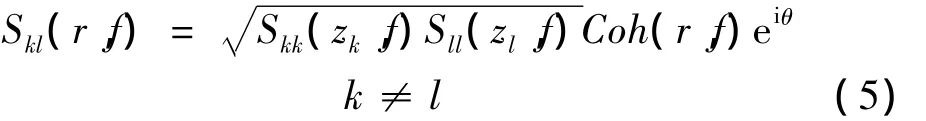
式中，Skk(zk，f)和 Sll(zl，f)为相距 r的空间两点自功率谱，由式(4)确定，θ(f)为互谱相位角。Coh(r，f)为相干函数，根据 Davenport建议采用竖向与横向相干函数:

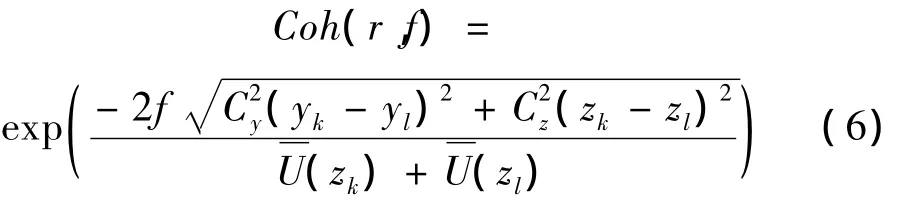
式中:yk，yl和zk，zl分别表示空间两点的横向坐标与竖向坐标，两点连线与平均风速的方向垂直(zk)与(zl)分别为高度在zk与zl处的平均风速，Cy与Cz为指数衰减系数，其值可由试验确定，它与平均风速、离地高度及地表面粗糙长度等有关。根据文献［14］，一般取 Cy=8，Cz=7。

根据Shinozuka理论［15］，结合FFT算法，可快速有效地模拟得到脉动风速时程样本［12］。因此风场中任意一点的风速可表示为:

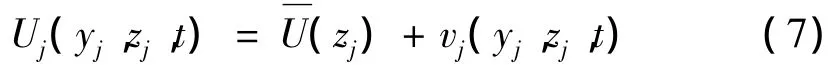
3 随机风场中覆冰导线舞动数值模拟

3.1 覆冰四分裂导线特征段线路

以200 m小档距和500 m大档距单档四分裂导线舞动为研究对象。导线型号为4XLGJ－400/50，物理参数见表1，在自重作用下导线初始张力均为24.11 kN，分裂导线相邻子导线间距为450mm，覆冰初始凝角为50°，导线最低点平均风速为10 m/s，随机风沿x方向垂直作用于导线上，如图4所示。

3.2 随机风场及空气动力载荷

要确定风荷载，首先模拟脉动风速时程样本。假设该特征段线路所处环境为B类地貌，地面粗糙系数a取 0.16，地面粗糙长度 z0取 0.03［14］。假设导线弧垂最低点位置离地高度10 m。在模拟风速时，沿顺线路y方向每隔10 m模拟一个风速时程样本。模拟时程总长 t=2000 s，时间步长 Δt=0.5 s，频率截取范围取0.0～6.28 rad/s，频率范围等分数 N=3000，即 Δω =0.00209 rad/s。模拟的基本风速U10取 10 m/s。

表1 新月形覆冰导线物理参数(冰厚:12mm)Tab.1 Physical parameters of conductor with crescent-shaped ice(ice thickness:12mm)

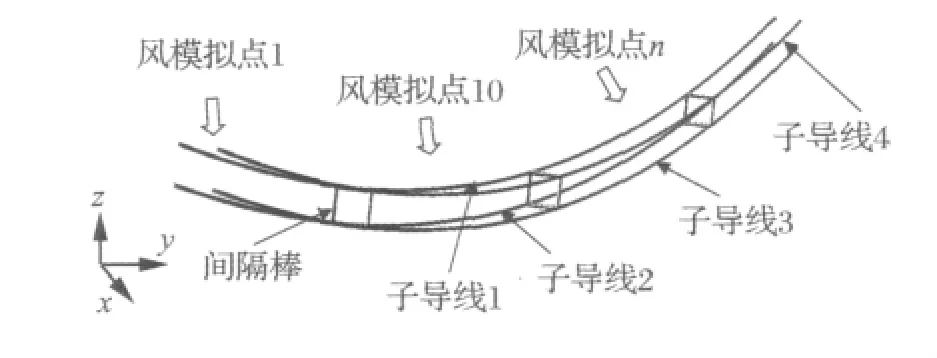
图4 覆冰四分裂导线模型Fig.4 Iced quad bundle conductor model

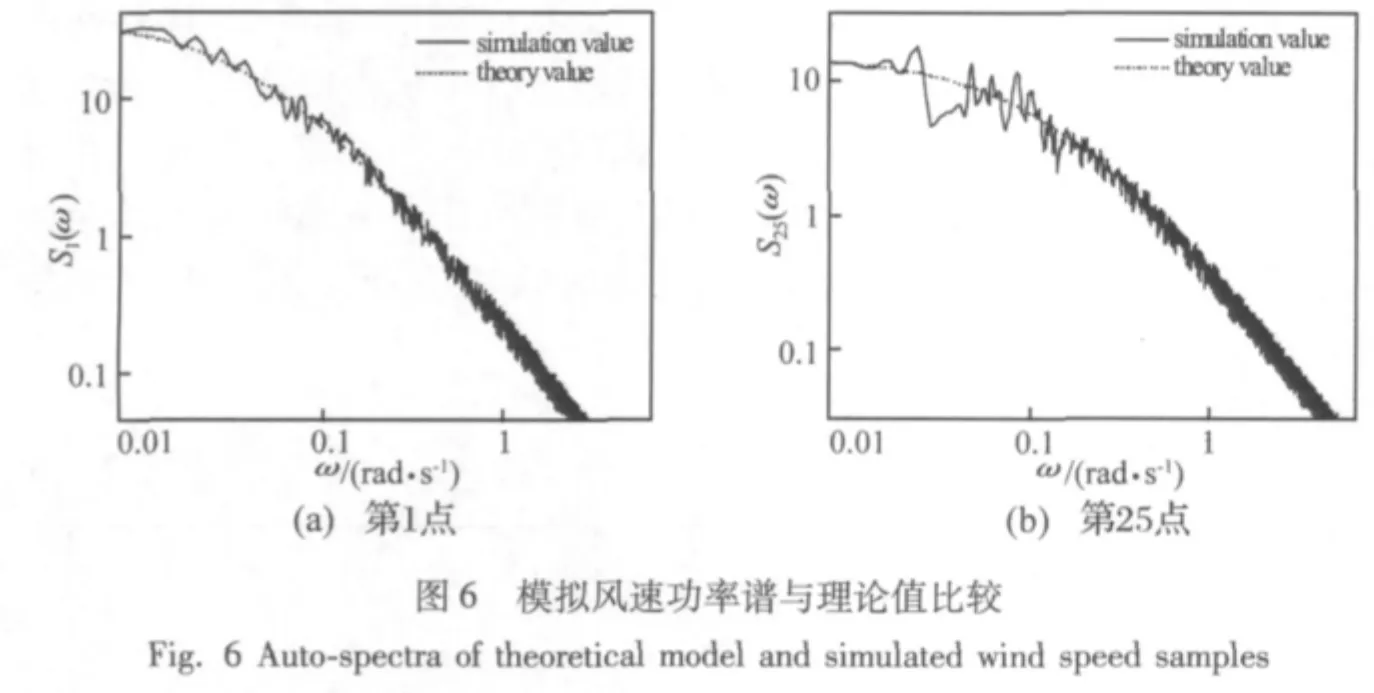
图5给出了500 m档距输电线路第1个和第25个模拟点的风速时程曲线。第1点为输电导线左端，第25个模拟点为输电线路中点。将模拟得到的脉动风速时程曲线进行谱分析可得到功率谱，该两点的模拟风速功率谱与Kaimal谱的理论值比较如图6所示，可见两者吻合较好。

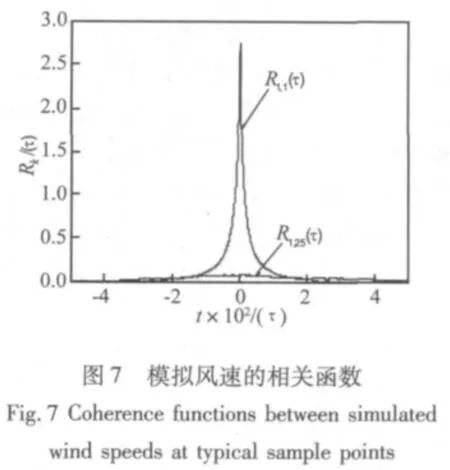
图7给出第1点的自相关函数和第1与第25点的互相关函数。可以看出，相隔250 m的第1和第25点风速的相关性较弱。说明数值模拟得到的风速时程样本合理。

根据式(1)，覆冰导线在风荷载作用下所受空气动力载荷可表达为:

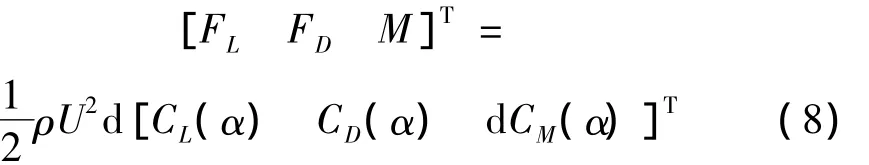
式中:空气动力系数CL，CD，CM随攻角α变化。覆冰导线运动过程中攻角的变化可由下式确定［6］:

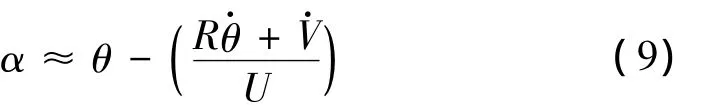
值得一提的是，由风洞试验仅测得在典型风速下各覆冰子导线的气动力系数，而在计算随机风速下气动力载荷时需要连续变化的不同风速下的气动系数。如前所述，覆冰四分裂导线各子导线的气动参数受风速影响很小，即可以取任意一种风速下的气动系数，或取平均值。更精确的方法则可以利用已知的不同风速下气动系数通过插值得到任意风速下的值。

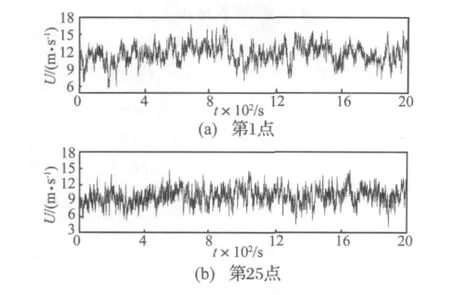
图5 模拟随机风速时程曲线Fig.5 Time historical curves of simulated stochastic wind speed at typical sample points

3.3 有限元模型

采用文献［11］提出的覆冰分裂导线舞动非线性有限元方法，模拟研究随机风场中导线的舞动，计算模型见图4。用具有扭转自由度的索单元离散各覆冰子导线;2节点空间梁单元模拟间隔棒;间隔棒与导线连接处采用梁索连接过渡单元。模拟覆冰导线的索单元长度取5 m，经单元收敛性检查，满足精度要求。线路两端的耐张绝缘子串采用杆单元模拟，其与杆塔连接的端部固定约束。忽略杆塔及变形影响。

首先利用由数值模拟得到的覆冰导线上各点的随机风速，根据各覆冰子导线的空气动力系数，由式(8)计算得到当前时刻作用于各点的气动载荷。导线运动过程中风攻角的变化由式(9)确定。材料参数见表1。

4 数值模拟结果分析

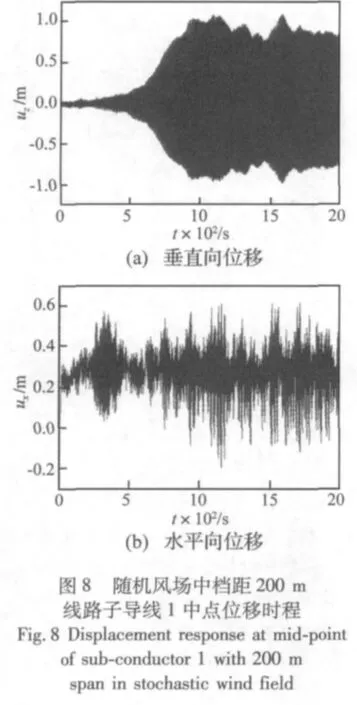
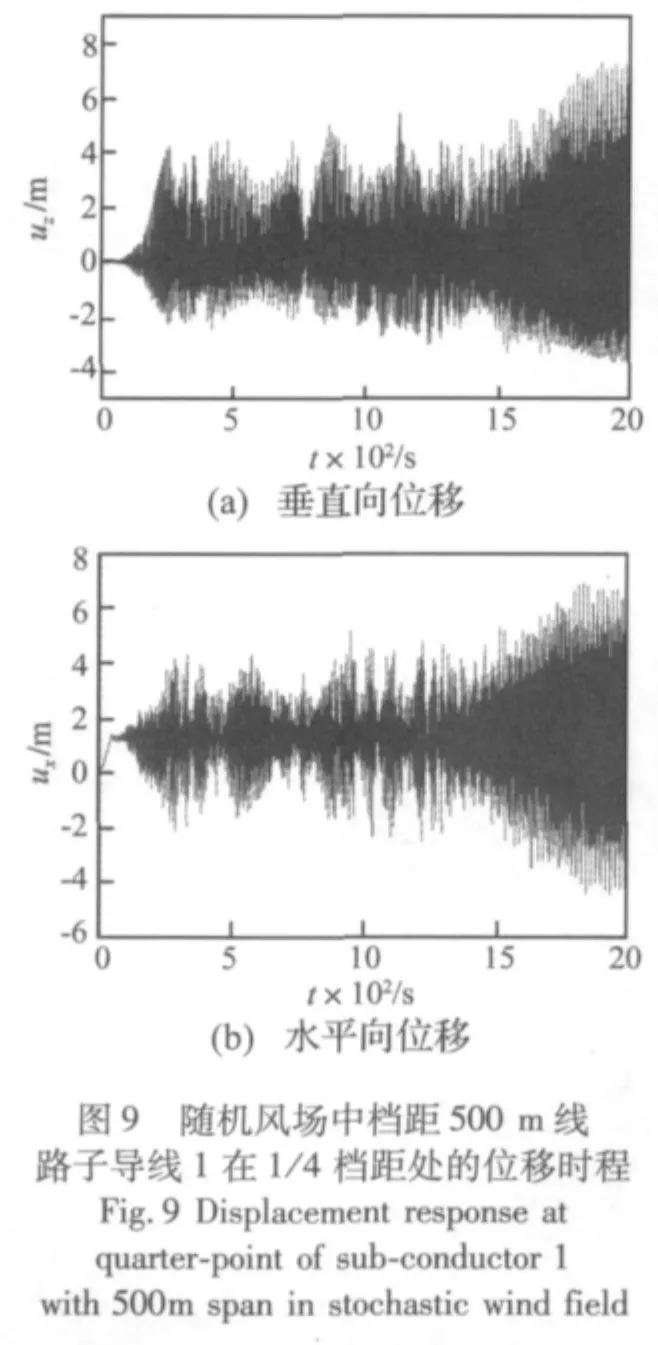
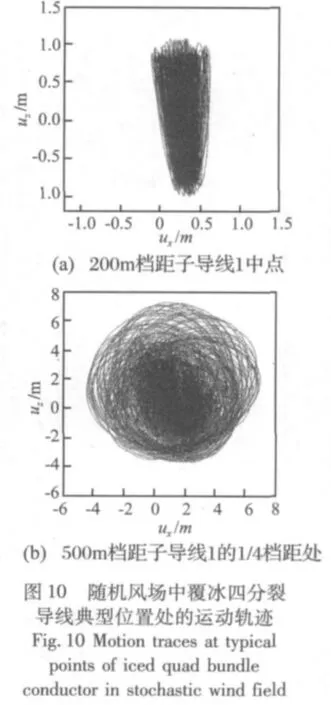
图8图9分别为随机风场中200 m档距和500 m档距线路典型点的位移时间历程，图10为典型点的运动轨迹。可见，随机风荷载作用下，覆冰导线发生了大幅度振动，其运动响应中包含了周期性舞动响应与随机阵风响应，同日本敦贺试验线路舞动现场观测结果一样［16］。

舞动是一种自激振动，其频率通常与覆冰导线的某一阶固有频率接近，而与阵风脉动风速的频率特性无关。阵风响应则是受迫振动响应，可分为低频准静态响应和高频动态响应两部分。脉动风的能量主要集中在低频率范围内，该部分对应的响应一般称为准静态响应，为受迫振动的主要成份。另一部分则对应于由脉动风湍流作用产生的频率较高的动力响应。

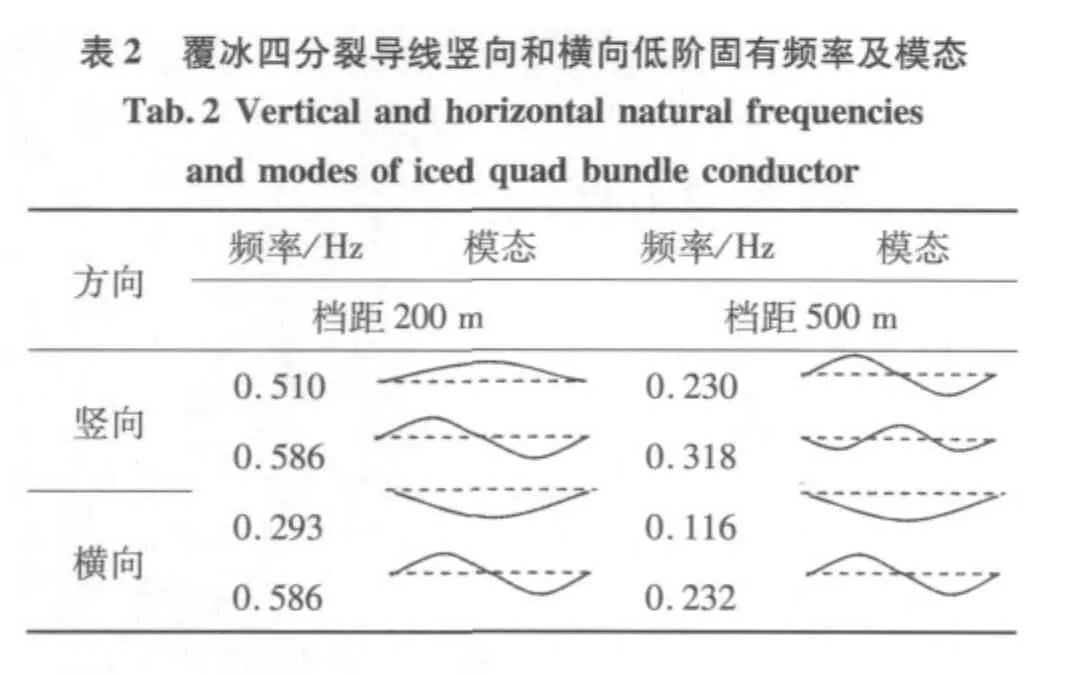
文献［11］较详细地讨论了稳定风作用下覆冰四分裂导线的舞动。按我国输电线路设计规程［17］，稳定风速取随高度变化的平均风速。表2列出了200 m档距和500 m档距线路覆冰导线竖向与横向低阶固有频率与模态。便于分析，图11～图14分别给出了200 m档距与500 m档距线路在稳定风及随机风作用下竖向与横向位移频谱分析结果。由图11可见，档距200 m线路发生舞动时，其频率接近于竖向基波模态对应的固有频率0.51Hz(见表2)，即导线发生了垂直舞动，运动模式为基波模态。其横向运动的主频与竖向相同。由图12可见，在随机风作用下，其舞动频率仍然接近于竖向基波模态对应的固有频率，对应的横向运动也有一相同频率的峰值。此外，横向运动还包含了低阶频率响应与频率接近0.293Hz的基波模态响应，这两部分频率响应成份与舞动无关，为阵风响应。即对于200 m档距线路，随机风场中导线的舞动模式及频率与稳定风下一致，均具相同特征。

对500 m大档距，由图13可见，导线的舞动仍然为垂直舞动，其舞动模式为双半波模式，频率接近于双半波模态固有频率0.23Hz(见表2)。图14表明，在随机风作用下导线的舞动频率接近于竖向三半波模态固有频率0.318Hz，对应的横向运动也有一相同频率的峰值。此外，横向运动还包含了低阶频率响应和频率接近0.116Hz的基波模态响应，这两部分频率响应为阵风响应。由此可见，随机风作用下500 m大档距线路的舞动模式为三半波，而稳定风下为双半波，舞动特征明显不同。

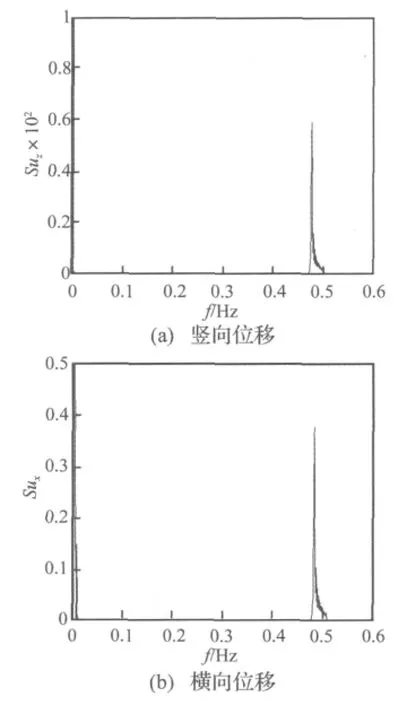
图11 稳定风作用下档距200 m线路子导线1中点位移频谱(风速:10 m/s)Fig.11 Power spectra of displacements at mid-point of sub-conductor 1 with 200m span in steady wind field(wind speed:10 m/s)

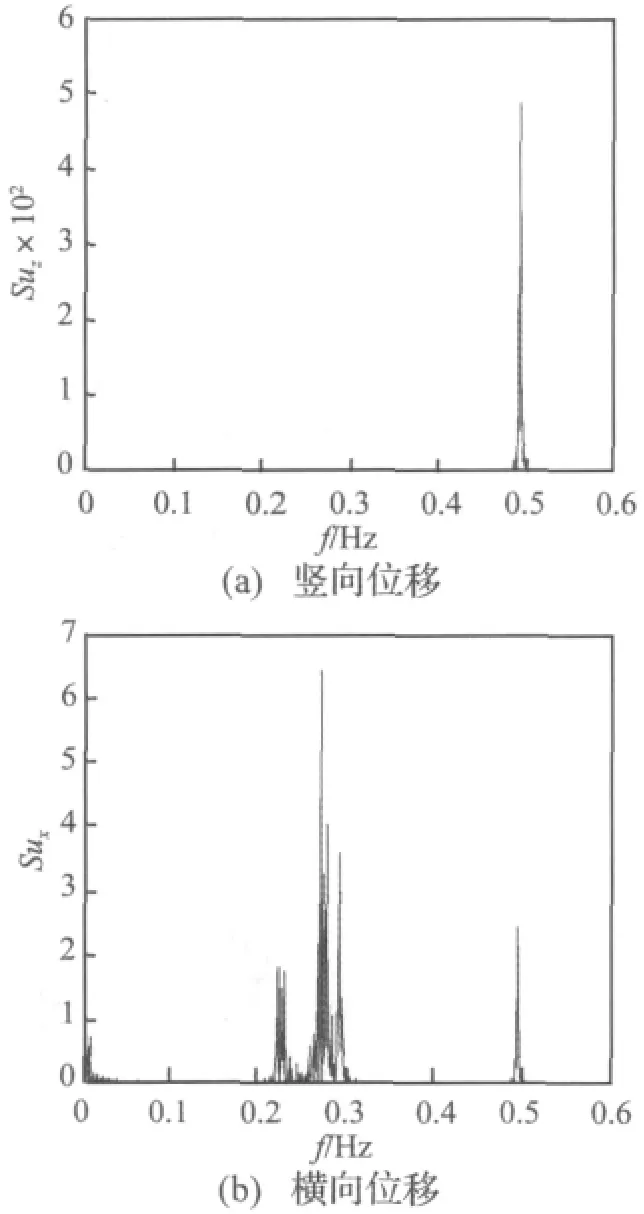
图12 随机风场中档距200 m线路子导线1中点位移频谱(基本风速:10 m/s)Fig.12 Power spectra of displacements at mid-point of sub-conductor 1 with 200 m span in stochastic wind field(basic wind speed:10 m/s)

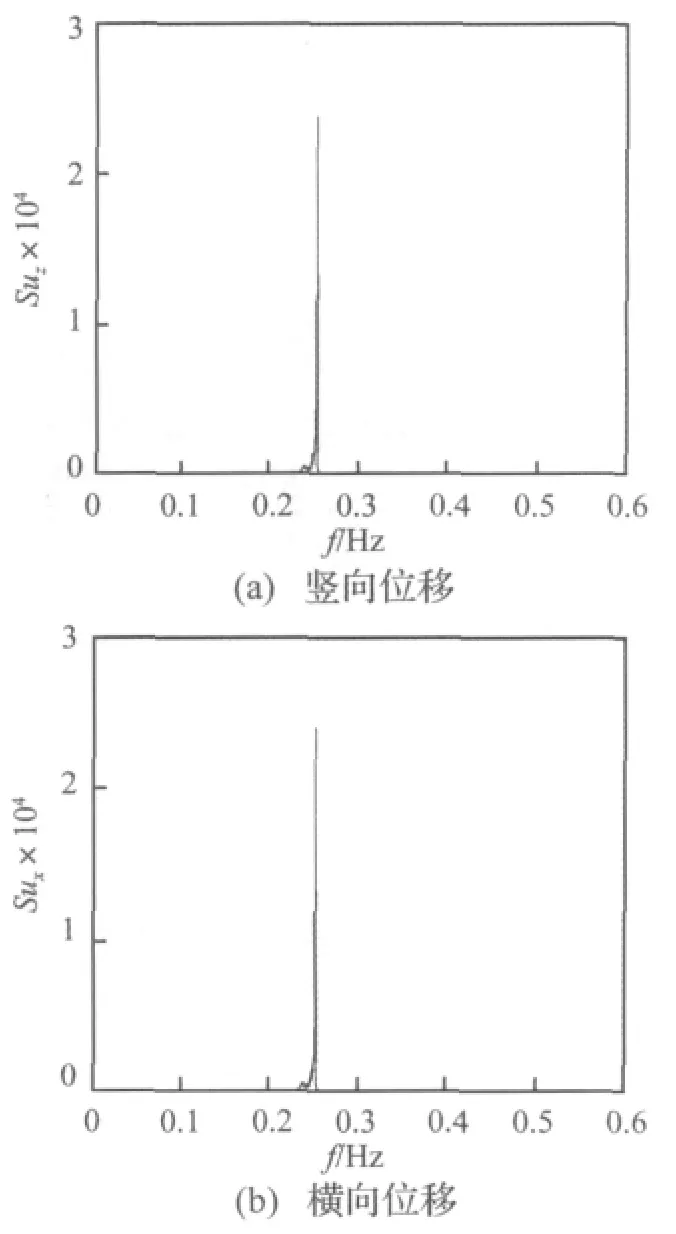
图13 稳定风作用下档距500 m线路子导线1在1/4档距处的位移频谱(风速:10 m/s)Fig.13 Power spectra of displacements at quarter-point of sub-conductor 1 with 500 m span in steady wind field(wind speed:10m/s)

?

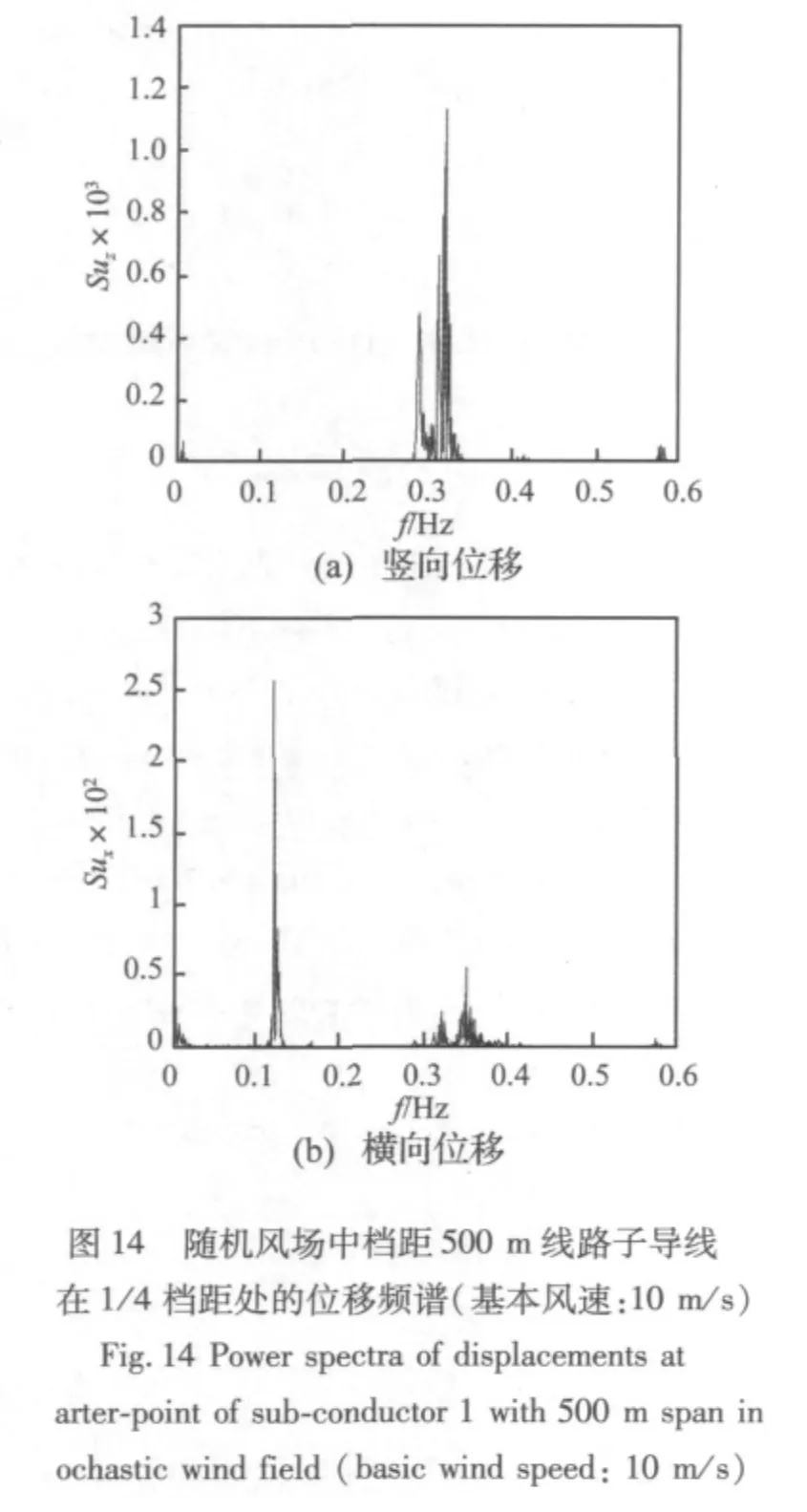
在随机风场的舞动分析中，考虑了风速随高度变化与空间相关性，在大档距情况下风速分布非均匀性更加突出，舞动特征更加复杂。舞动特征是舞动防治方法研究需考虑的关键因素，因此，大档距情况下舞动的研究考虑风场随机性是必要的。

5 结论

本文采用由风洞试验获得的典型新月形覆冰四分裂导线空气动力系数，应用数值模拟方法研究在随机风场中覆冰四分裂导线的舞动。结果表明，随机风场中覆冰导线的振动响应包含了舞动自激振动响应与阵风受迫振动响应。小档距导线的舞动模式与稳定风情况一致，而大档距时可能出现更高阶的舞动模式。因此，在研究大档距线路舞动时，须考虑风场的随机性。这对大档距线路舞动防治技术的研究具有重要意义。

［1］Hartog J P D.Transmission line vibration due to sleet，trans［J］.AIEE 51(Part 4)，1932:1074－1086.

［2］Nigol O，Clarke G J.Conductor galloping and control based on torsional mechanism［C］.New York，IEEE Power Engng Soc.Meeting，1974，C74016 －2.

［3］Desai Y M，Yu P，Popplewell N，et al.Finite element modeling of transmission line galloping［J］.Computers ＆Structures，1995，57(3):407 －420.

［4］Luongo A，Zulli D，Piccardo G.A linear curved-beam model for the analysis of galloping in suspended cables［J］.Journal of mechanics of materials and structures，2007，2(4):675－694.

［5］Luongo A，Zulli D，Piccardo G.Analytical and numerical approaches tononlineargallopingofinternally resonant suspended cables ［J］.Journal of sound and Vibration，2008，315:375－393.

［6］Zhang Q，Popplewell N，Shah H.Galloping of bundle conductor［J］.Sound and Vibration，2000，234(1):115－134.

［7］何 锃，赵高煜.安装防振锤的分裂导线自由振动的有限元计算［J］.工程力学，2003，20(1):101 －104.

［8］严 波，李文蕴，张宏雁，等.覆冰双分裂导线舞动数值模拟方法［J］.重庆大学学报(自然科学版)，2009，32(7):787－792.

［9］严 波，李文蕴，周 松，等.覆冰四分裂导线舞动数值模拟研究［J］.振动与冲击，2010，29(9):102－107.

［10］Liu X H，Yan B，Zhang H Y，et al.Nonlinear numerical simulation method for galloping of iced conductor［J］.Applied mathematics and mechanics，2009，30(4):489－500.

［11］刘小会，严 波，张宏雁，等.分裂导线舞动非线性有限元分析方法［J］.振动与冲击，2010，29(6):129 －133.

［12］Yan B，Lin X，Luo W，et al.Numerical study on dynamic swing of suspension insulator string in overhead transmission line under wind load［J］.IEEE Transactions on Power Delivery，2010，25(1):248 －259.

［13］张宏雁，严 波，周 松，等.覆冰四分裂导线静态气动力特性试验研究［J］.空气动力学报，2011，29(2):23－27.

［14］Simiu E，Scanlan R H.Wind effects on structures(2rd edition)［M］.New York:John Wiley＆ Sons，1986.

［15］Shinozuka M， Jan C M. Digital simulation of random processes and Its applications［J］.Journal of Sound and Vibration，1972，25(1):111－128.

［16］Gurung C B，Yamaguchi H，Yukino T.Identification and characterization of galloping of tsuruga test line based on multi-channel modal analysisoffield data［J］. Wind Engineering，2003，91:903－924.

［17］国家电力公司东北电力设计院.电力工程高压送电线路设计手册［M］.北京:中国电力出版社，2003.