相关机械振源的盲源分离方法

周晓峰，杨世锡，甘春标

(浙江大学 机械系＆液压传动及控制国家重点实验室，杭州 310027)

独立分量分析(Independent component analysis，ICA)是近年来快速发展的一种新的统计信号处理方法。它在源信号和传播特性都未知的情况下，将多个观测信号按照统计独立原则通过优化算法分解为若干尽可能独立的成分，以获得对源信号和分离矩阵的估计。基于独立分量分析的盲源分离方法，在机械设备状态监测与故障诊断领域已广受关注［1－7］。源信号满足统计独立性的假设条件是准确分离源信号的前提之一。在机械振源的盲源分离应用中，一般将不同机器［7］或不同部件［6］的激励响应视为源信号，而不同激励对于同一部件的响应可能因为存在交叉的频率成分而不满足源信号的统计独立性假设，因而用标准的ICA方法往往无法准确分离源信号。

在相关振源信号的部分子带满足统计独立的假设前提下，本文提出了一种基于小波包分解的相关机械振源的盲源分离方法。该方法首先将观测信号用小波包分解成子带信号;分别计算各个子带内信号的互信息，选择互信息较小的几个子带信号重构成新的观测信号;用独立分量分析方法估计新观测信号的分离矩阵;最后用该矩阵分离原始观测信号，实现相关机械振源信号的分离。

1 信号模型

设 s=［s1，s2，…，sp］T是一组相互独立的源信号，x=［x1，x2，…，xq］T为一组观测信号，x 中的各分量由 s中的源信号线性组合而成，用矩阵表示为:

式中，H为一个的列满秩q×p矩阵，b为维加性测量噪声信号。

独立分量分析方法从已知的观测x出发，根据独立性测度函数，寻求线性变换 W=［w1，w2，…，wq］≜H－1，使得变换后的信号尽可能的独立［8］:

相关源信号不满足统计独立假设因而无法用标准的ICA准确地分离出源信号。观测信号可以表示为其子带分量的组合，不考虑噪声且观测信号的个数和源信号的个数相等时，式(1)可以改写为［9］:

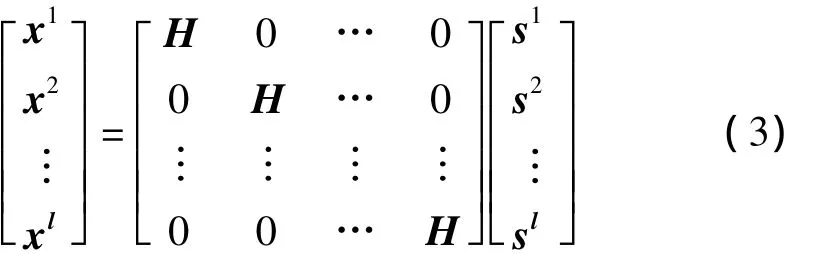
假设源信号s在通带内是相关的，但是存在若干个相互独立的子带。不妨假设在第j个子带上是独立，则可在该子带内用标准的ICA方法估计分离矩阵W。

2 源相关性的影响

Hyvarinen［10］提出的基于负熵极大化判据和固定点迭代的快速算法(FastICA)是一种数值稳定、收敛速度较快、鲁棒的经典ICA方法。但是该方法分离相关源信号时，源信号的相关程度严重影响其分离效果。相关源仿真信号为:

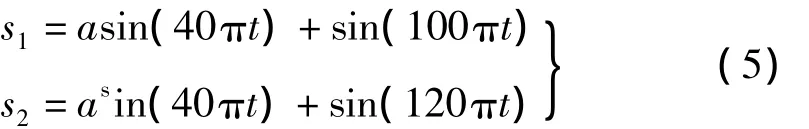
式中，a是实常数。

源s1和s2的相关系数为:

相关系数是实常数α的函数，α分别取不同值时的源信号用相同混合矩阵混合，得到一系列观测信号，用FastICA算法直接对观测信号进行分离。ICA方法的分离效果采用 Amari［11］提出性能指标(Perfomance Index，PI)来衡量。

式中 pij=［WH］ij，0≤PI≤2，PI等于 0 时源信号完全分离，PI值越大分离效果越差。

仿真信号的分离性能和源信号相关系数的关系如图1所示。从图中可以看出分离性能PI随着相关系数r的增加而下降，a=0.35，源 s1和 s2的相关系数r为0.1081，FastlCA算法分离结果的 PI为0.3028。

图1 分离性能和相关系数的关系曲线Fig.1 Curve of Perfomance Index vs correlation coefficient

图2为a=0.35时源信号(s1和s2)和分离的源信号(y1和y2)的幅值谱。从图中虚线椭圆所标记处，可以看出分离的源信号间依然存在较明显的混叠。一般来说，当PI小于0.1时，ICA方法的分离效果较好;0.1＜PI＜0.2时，分离结果勉强可以接受;而 PI大于0.2时，可以认为分离失败。

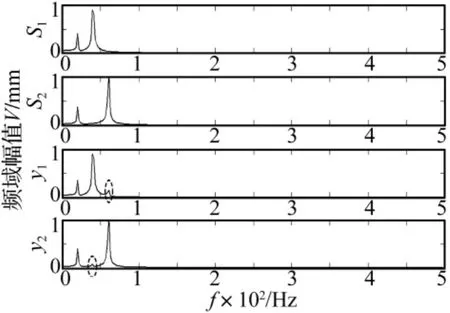
图2 a=0.35时源信号和分离源信号的幅值谱Fig.2 Magnitude spectra of rve of souces signals and separated sources signals when a=0.35

3 基于小波包分解的相关振源分离方法

ICA中的信号模型是线性的，因此在ICA方法中，常用线性滤波来降噪或提高源信号的独立性。观测信号经过线性滤波器Fj后，可以表示为:

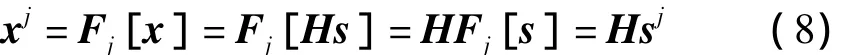
式(8)表明，对于相关源的混合信号，其混合矩阵H或分离矩阵W可以由独立子带的观测信号用ICA方法估计得到。

4 小波包分解

假定共轭滤波器h(n)满足，Σ h(n－2k)(n－2l)=δkl;令 g(k)=(－1)kh－k+1，定义一列递归函数{μk}，(k=0，1，2，…):

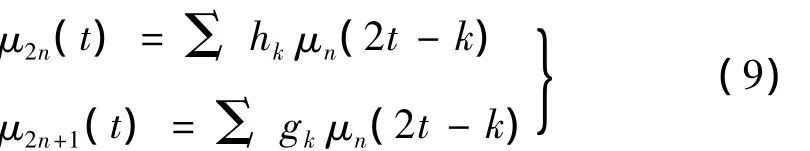
式中:μ0(t)定义为尺度函数φ(t);μ1(t)为小波基函数φ(t)，称 μn(t)(n=2l或 n=2l+1，l=0，1，2，…)为正交尺度函数 φ(t)的小波包［12］。

小波包分解能够根据被分析信号的特征，通过一组累接的共轭正交滤波器将频带进行多层次划分，自适应地选择相应频带，使之与信号频谱相匹配。

观测信号的n层小波包分解后可以表示为:

相应的源信号可以表示为:

则式(3)可以表示为:

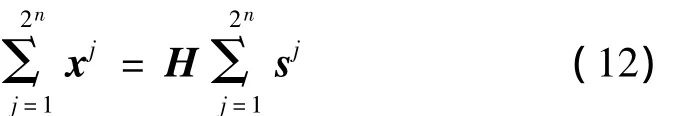
5 独立子带的选择和重构观测信号

互信息是一组随机变量是否统计独立的主要测度之一。互信息是非负的，只有当互信息为零时，一组随机变量才是统计独立的。文献［13］中证明了子带观测信号xj的互信息最小表示子带源信号的互信息最小，即统计独立。

Cardoso在文献［14］中给出了互信息近似计算公式:

式中，cum(* ，*)、cum(* ，* ，*)和 cum(* ，* ，* ，*)分别是xj的二阶、三阶和四阶互累积量。

选择归一化互信息小于阈值的k个子带重构观测信号 xrec，则:

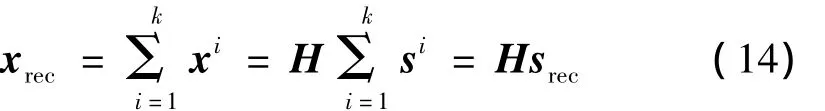
式中，srec为重构的独立源信号。

6 分离矩阵估计和源信号分离

对重构的观测信号xrec，用FastICA算法估计分离矩阵W。用分离矩阵W乘以原始观测信号x就可以实现相关源信号的分离。

7 仿真研究

引发旋转机械设备异常振动的故障源都会产生一定频率成分的振动，可能是单频的，也可能是一组频率或某个频带。一般来说不对中不但影响基频振动，还可能引发2倍频及其他高频振动;滑动轴承油膜涡动的振动频率为基频的(0.42～0.48)倍;转子组件的松动振动频率以基频为主，可能伴有倍频或1/2倍频、1/3倍［15］。假设一台旋转机械的基频f0=50Hz，构造其不对中、油膜涡动和组件松动的故障振动仿真源信号s1，s2和s3，以及高斯噪声源信号s4。

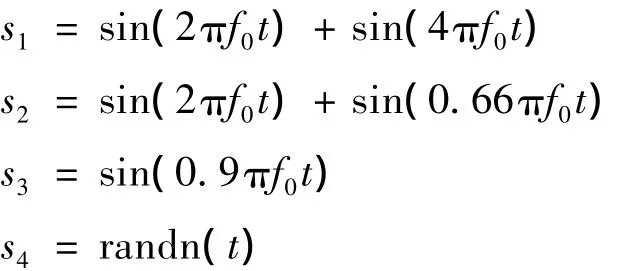
其中s1和s2是相关源。

混合矩阵

仿真信号的采样频率为1000Hz，采样时间1 s。图3为源信号0～0.25 s的时域波形，其中图3(a)～图3(d)分别是源信号s1，s2，s3和s4的时域波形。

混合信号直接用FastICA算法分离性能指标PI=0.2462。分离的源信号时域波形如图4，其中图4(a)～图4(d)分别是FastICA分离的源信号y1，y2，y3和y4的时域波形。

由于相关源信号s1和s2存在，FastICA分离的源信号y1和y2仍然是源信号s1和s2混合信号，如图4(a)和图4(b)。

比较图3和图4中还可以发现，对于既有相关源又有独立源的观测信号，FastICA还是能够较好地分离出独立的源信号。噪声源一般和机械振动源是独立的，如果能准确估计源(包括相关源和独立源)的数目，选择同数量的观测信号，直接用ICA方法就能分离噪声源;如果机械振动源都是相关的，只需两路观测信号，ICA方法就能实现降噪。

新方法中选用Daubechies小波函数的db8函数共轭正交滤波器组对观测信号进行正交小波包分解，小波包分解的层数n=4。互信息是随机变量之间依赖性的自然量度。它总是非负的，当且仅当变量之间统计独立时为零，新方法中子带互信息的阈值取文献［13］建议的0.05。新方法分离的源信号的时域波形如图5，其中图5(a)～图5(d)分别是新方法分离的源信号和的时域波形。从图3和图5可以看出较好地分离出源信号;和分别对应于源信号s4，s2，s3和s1，其中的次序不一致和反相是由ICA方法内在的不确定性产生的。新方法的分离性能指标PI=0.0392，这也说明几乎实现了源信号的完全分离。

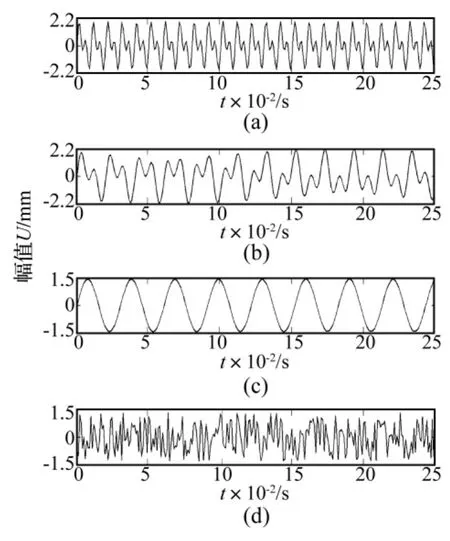
图3 源信号的时域波形Fig.3 Timewave of sources signal

图4 FastICA分离的源信号时域波形Fig.4 Timewave of sources signals separated byFastICA

图5 新方法分离的源信号时域波形Fig.5 Timewave of sources signals separated by new method

8 结论

机械系统中，相关源和不相关源往往以相互混合的方式同时存在传感观测中。传统盲源分离在机械振源的分离中略显不足。本文提出了一种基于小波包分解的相关机械源盲源分离方法。该方法首先按照互信息标准重构相关性较小的若干小波包分解子带局部观测信号;然后利用该局部观测信号估计分离矩阵;最后用该矩阵分离矩阵作用于原始观测信号实现相关机械振源信号的分离。旋转机械中的相关振动源故障的仿真信号振源信号验证了该方法在相关机械振源分离中的有效性。新方法对于相关振源，特别是具有因果关系的故障振源的分离具有一定的应用前景。

波包分解的层数是新方法性能的关键参数之一。分解的层数过小重构的局部子带信号中仍然是相关信号的混合，从而分离效果欠佳;分解的层数过大会导致算法性能退化。实际应用中需要源信号的先验知识;或改进方法使其能根据小波包分解的节点处的互信息自适应的确定分解层数。

［1］蔡艳平，李艾华，石林锁，等.基于盲解卷积的柴油机振动信号分离研究［J］.振动与冲击，2010，29(9):38－41，240.

［2］Liu X，Randall R B，Antonl J.Blind separation of internal combustion engine vibration signals by a deflation method［J］.Mechanical Systems and Signal Processing，2008，22(5):1082－1091.

［3］叶红仙，杨世锡，杨将新.振动源信号的快速二阶统计量算法研究［J］.振动与冲击，2008，27(7):79－82.

［4］Antonl J.Blind separation of vibration components:Principlesand demonstrations［J］.Mechanical Systems and Signal Processing，2005，19(6):1166－1180.

［5］胥永刚，张发启，何正嘉.独立分量分析及其在故障诊断中的应用［J］.振动与冲击，2004，23(2):104－107.

［6］陈仲生，杨拥民，沈国际.独立分量分析在直升机齿轮箱故障早期诊断中的应用［J］.机械科学与技术，2004，(4):481 －483.

［7］Gelle G，Colas M，Serviere C.Blind source separation:a tool for rotating machine monitoring by vibrations analysis?［J］.Journal of Sound and Vibration，2001，248(5):865－885.

［8］Hyvarinen A，Karhunen J，Oja E.Independent component analysis［M］.New York:John wiley＆ Sons InC.，2001.

［9］Tanaka T，Cichocki A.Subband decomposition independent component analysis and new performance criteria［C］.proceedings of the Acoustics，Speech，and Signal Processing，2004 Proceedings (ICASSP'04) IEEE International Conference on，2004.

［10］Hyvarinen A.Fast and robust fixed－point algorithms for independent component analysis［J］.Neural Networks，IEEE Transactions on，1999，10(3):626－634.

［11］Amari S，Cichocki A，Yang H H.A new learning algorithm for blind signalseparation［J］. Advances in Neural Information Processing System，1996:1 －7.

［12］杨宗凯秦前清.实用小波分析［M］.西安:西安电子科技大学出版社，1998.

［13］Kopriva I，Sersic D.Wavelet packets approach to blind separation of statistically dependent sources ［J］.Neurocomputing，2008，71(7－9):1642－1655.

［14］Cardoso J F.Dependence，correlation and gaussianity in independent component analysis［J］.J of Machine Learning Rearch，2003(4):1177 －1203.

［15］陈 进.机械设备振动检测与故障诊断［M］.上海:上海交通大学出版社，1999.