基于饱和约束LMS算法的磁悬浮隔振器控制研究

陈 昊，王 永，李嘉全，鲁 洋

(1.中国科学技术大学 自动化系，合肥 230027;2.中国科学院 长春光学精密机械与物理研究所 航测部，长春 130033)

在振动控制中，由于低频振动波较长，对其控制较困难。如果仅考虑用被动控制技术，好效果难以达到。最小均方(LMS)算法以其算法简单、计算量小、易于实现等优点，在振动主动控制中得到广泛的应用。

在现实条件下，控制过程会遇到各种约束，如一种典型的约束就是控制量饱和约束。该约束可能由多个因素产生，如控制器本身的限制、为保护作动器的考虑等。为了解决这一问题，最常用的一种处理饱和约束的方法就是直接对控制器输出信号(作动器的驱动信号)进行限幅。而限幅将会产生多个倍频信号，如果将它施加到隔振器系统上，当倍频信号中存在与隔振器系统共振频率接近的信号时，很容易引起系统共振，非但起不到减振效果，反而会造成对象振动量的加大。国内外针对这类含有饱和约束的问题也提出了一些算法，如Rafaely［1］算法。这种算法要得到很好的抗饱和效果，在惩罚函数设计时需要留有一定的预量，但预量的大小是很难确定的;同时这种算法需要分段更新抽头向量，容易引入倍频信号。

1 LMS算法

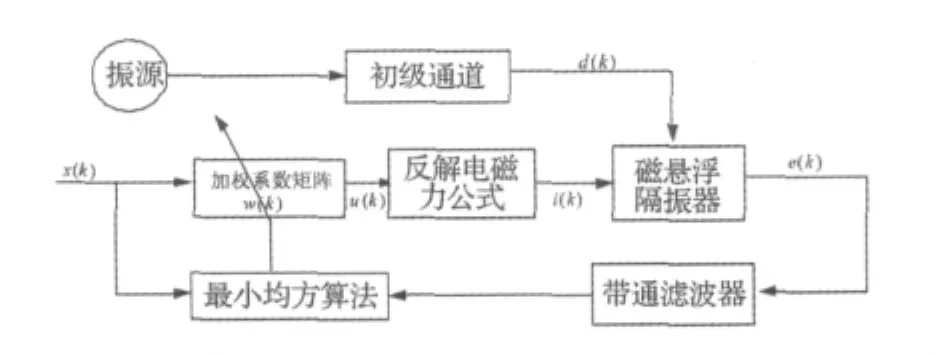
图1 自适应前馈振动主动控制系统Fig.1 Schematic diagram of adaptive feediorward control system

则控制器设计方法即为标准的LMS算法。

2 抗饱和LMS算法改进

LMS算法并没有考虑作动器饱和约束问题，因此得到的控制量可能远远大于作动器的允许输入幅值。为了保护作动器，它的输出控制量必须满足如下关系式:

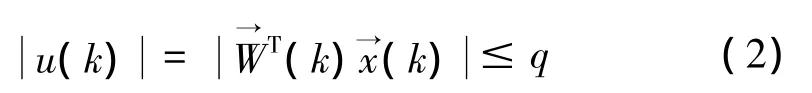
一种简单的方法是对控制量信号进行限幅。这种方法可以达到很好的抗饱和性，但其产生的倍频信号容易激起减振系统共振，非但不能起到减振的效果，还会造成对象振动量的加大，甚至损坏作动器。

文献［1］提出一种在代价函数中加入惩罚函数的方法。其中饱和约束下的控制器设计等价于如下性能指标的最小化:

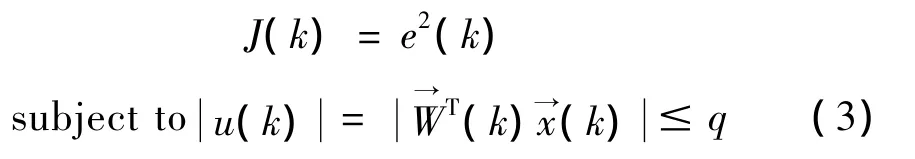
将约束项转变成惩罚项加入到代价函数中，得到含有惩罚项的代价函数:

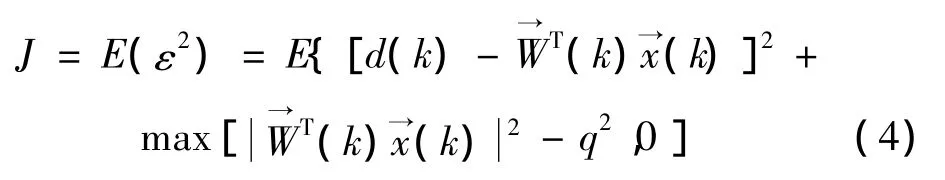
由于饱和约束函数是分段函数，在求控制律时也分段考虑。

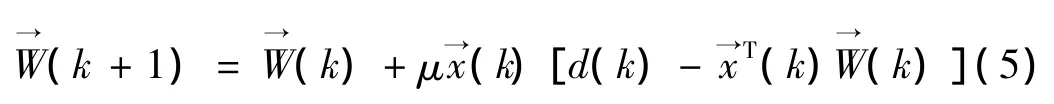
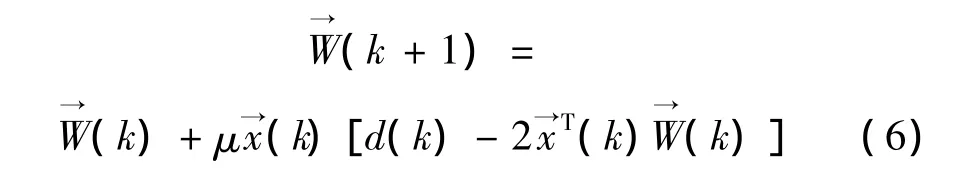
由于加入惩罚函数的代价函数是一个分段函数，当控制量没有超出饱和值(即时，惩罚项不起作用。只有当控制量超出饱和值(即时，才开始对代价函数进行惩罚。所以，如果要取得很好的抗饱和效果，q的取值要低于饱和值，即留有一定预量，但预量的大小很难确定。

将Rafaely抗饱和算法运用在磁悬浮隔振器上，对于q的选择是一个难点，如果q值选择过小，虽然可以满足抗饱和效果，但要损失一定的减振效果，如果q值选择过大，则很容易引起磁悬浮隔振器共振，使控制效果变坏。因此，研究一种在不依赖于q值选择的情况下可达到很好抗饱和效果的算法尤为必要。

为取得好的抗饱和效果，当控制量小于饱和约束时，就应该对代价函数进行小的惩罚，而当饱和约束超过饱和值时，对代价函数的惩罚急剧增大。据此，本文提出一种加入连续惩罚函数的方法，这种算法不仅具有很好的抗饱和效果，同时产生的其它倍频信号也很小，可忽略。其中选择连续惩罚函数为:

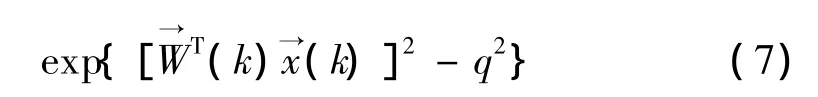
将约束项转变成惩罚项加入到代价函数中，得到含有惩罚项的代价函数:

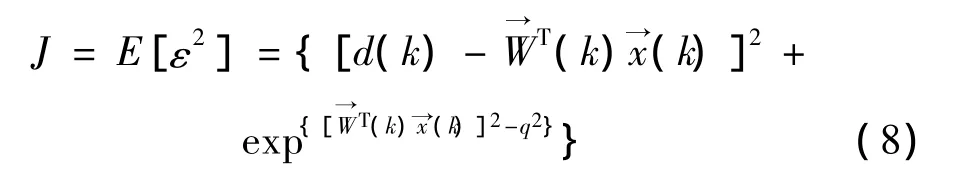
对其求偏导可得梯度向量瞬态估计为:

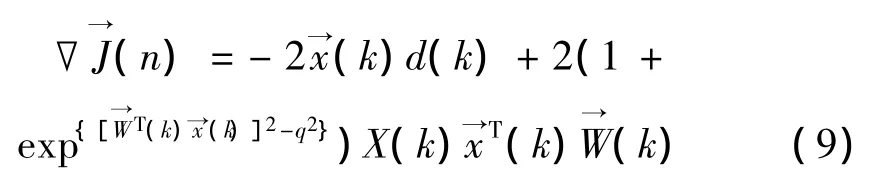
最后得到一个新的更新抽头向量的递归关系式为:

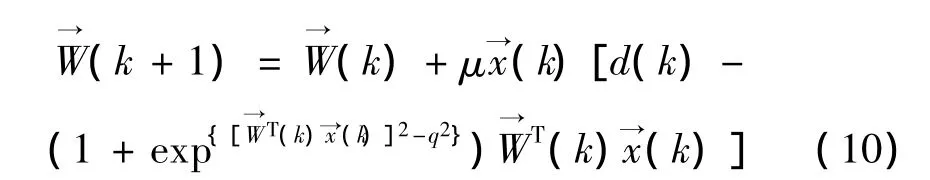
3 仿真与实验

3.1 系统仿真

通过MATLAB编程，对上述三种方法，即限幅算法、Rafaely算法以及加入连续惩罚函数算法，进行仿真实验。实验条件为:

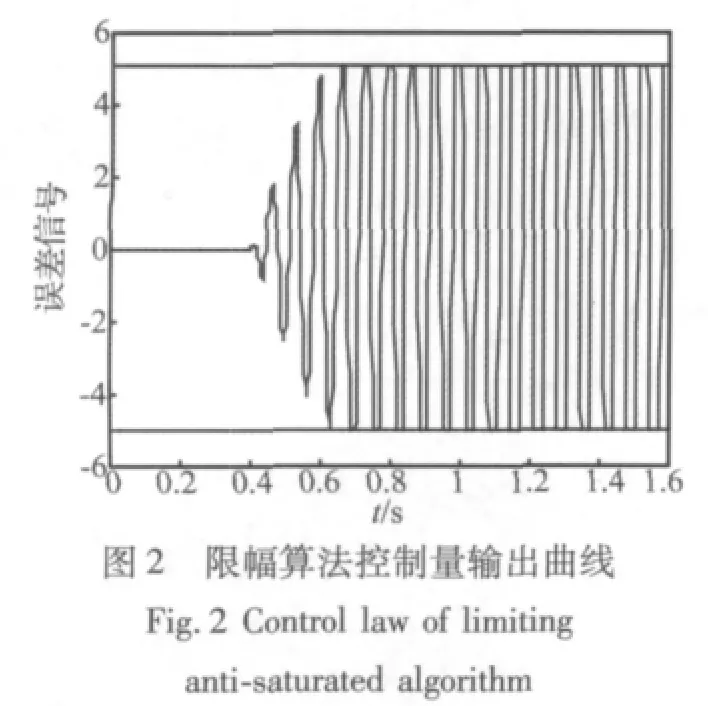
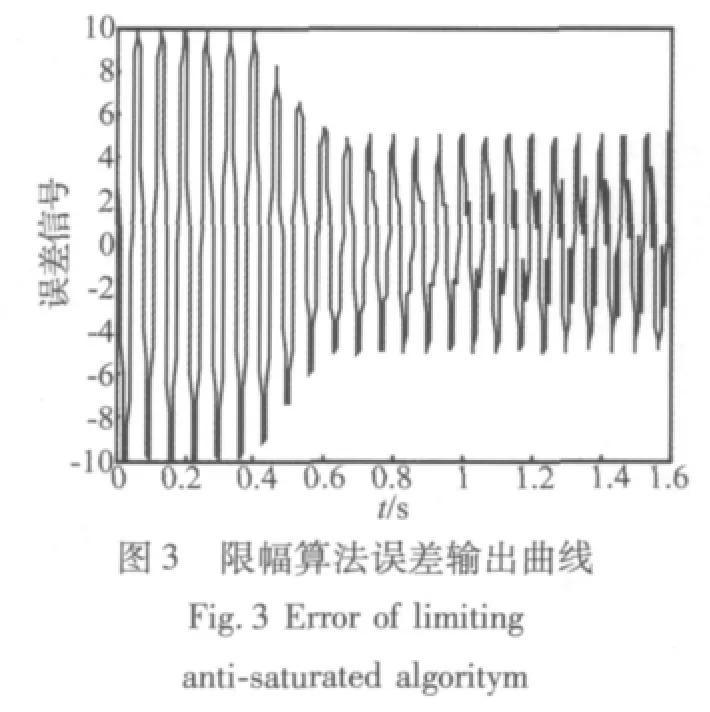
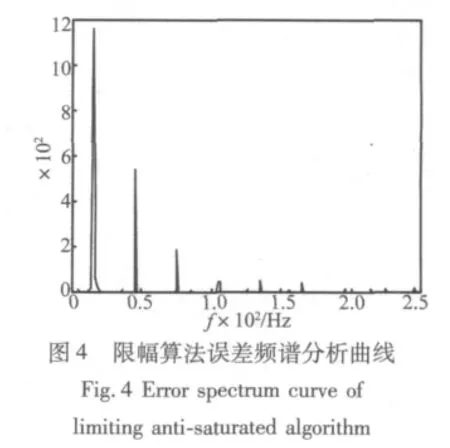
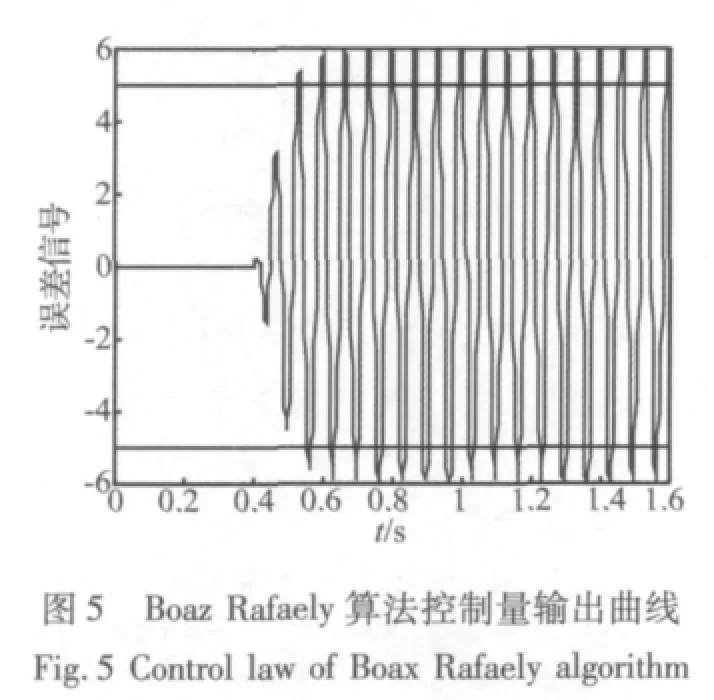
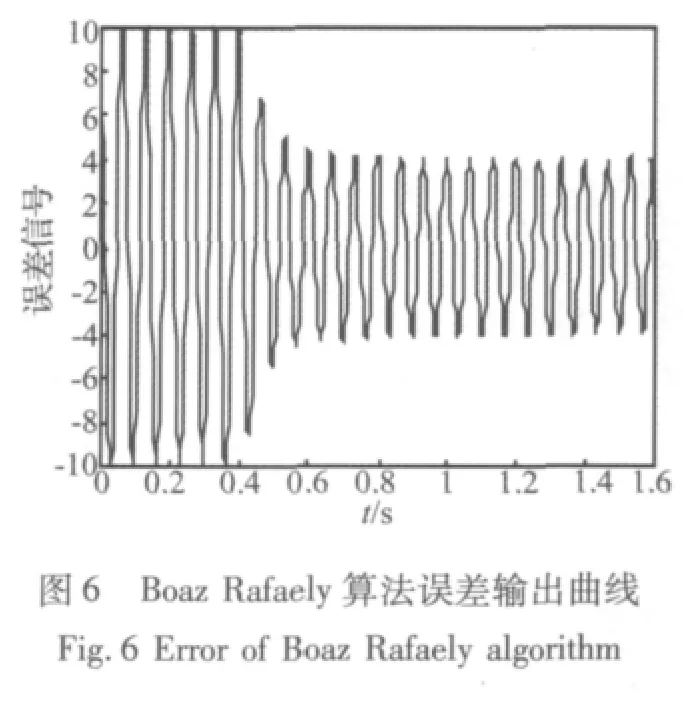
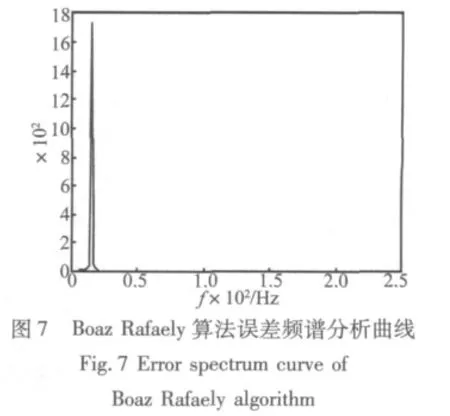
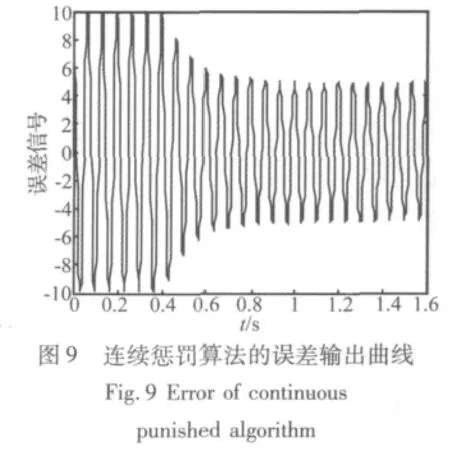
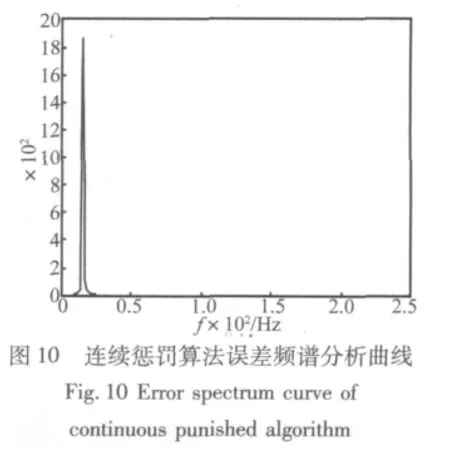
输入:U(n)=sin(0.1884n)，期望输出:d(n)=10sin(0.1884n+1.9)，饱和值:q=5，采样周期:0.002 s，步长因子:0.005，频率:15 Hz，仿真曲线见图 2～图10。

由于仿真中输入的是单一频率的正弦曲线，经过抗饱和减振环节后所产生的倍频信号都是因为抗饱和环节的非线性引起的，三种抗饱和算法的抗饱和性能和误差信号中倍频信号的幅值决定了算法的优劣。根据MATLAB仿真曲线，通过比较分析得:限幅抗饱和算法虽然可以达到绝对的饱和，即满足控制量输出不超出饱和值，但误差信号由多种倍频信号组成，其中倍频信号在三种算法中幅值也最大。Rafaely算法的抗饱和性和q与饱和值之间的预量决定，预量过小则抗饱和性能差，预量过大，则要损失一定的减振性能，同时误差信号的倍频信号会增加，所以预量很难确定，本文中的仿真曲线运用文献［1］中的参数，即q与饱和值相同。同样也会产生倍频信号，其幅值相比限幅抗饱和算法小，但比加入连续惩罚函数抗饱和算法大。加入连续惩罚函数的抗饱和算法不仅可以使误差信号是单一频率的正弦信号，而且控制量基本控制在低于饱和约束值5以下，同时产生的倍频信号幅值也是最小的。运用该方法设计的自适应前馈控制律可得到很好的抗饱和控制效果。

3.2 实验装置介绍

该实验系统由三个模块组成:机械模块、电控模块和激振模块。原理如图11所示。

机械模块包括磁悬浮隔振器、弹性基座、负载、基础以及支撑基础的弹簧等装置。电控模块包括PC机、数据采集卡、数模转换卡、功率放大器、三个传感器(一个位移传感器、一个加速度传感器和一个阻抗头)及配套的信号调理电路、动态信号分析仪。激振模块包括激振器、配套的功率放大器以及为功率放大器提供输入信号的信号发生器。其中，隔振器刚度k=28800 N/m，负载质量m=500kg。基础刚度kB=320000 N/m，基础质量mB=1000kg。

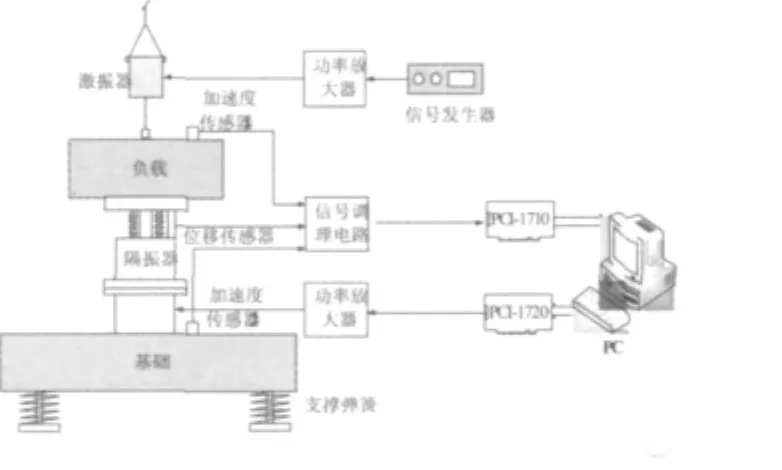
图11 磁悬浮隔振系统原理图Fig.11 Diagram of electromagnetic suspension vibration isolator

按照实验原理图连接磁悬浮隔振系统各个部件。PC机通过PCI1710板卡采集四路信号，基础加速度信号用于生成误差信号，相对位移信号用于计算电磁作动器的气隙大小，负载加速度信号用于监测负载加速度的变化，激振模块信号发生器的输出信号用作参考信号;通过PCI1720板卡输出两路信号，经过功率放大器后用于驱动上下两块电磁铁。

实验步骤如下:

(1) 实验系统加入7 Hz的激振力，幅值为A=0.3 cm，饱和值设定为 q=0.15 cm，系统采样频率为1000 Hz，20 s钟后施加主动控制;

(2)对磁悬浮隔振系统分别施加上述三种抗饱和LMS算法，通过PC机获取实验数据。

4 实验结果

实验效果如图12、图13、图14所示。

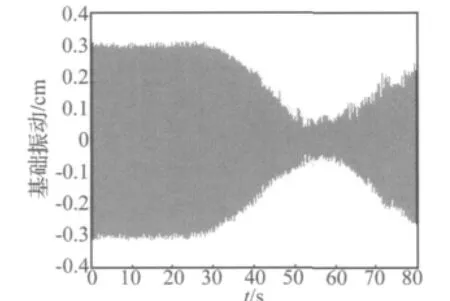
图12 限幅抗饱和算法Fig.12 Experimental results of anti-saturated algorithm

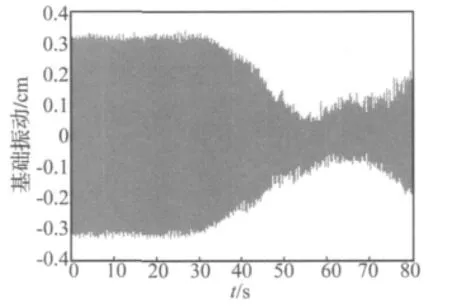
图13 Boaz Rafaely抗饱和算法Fig.13 Experimental results of Boaz Rafaely algorithm

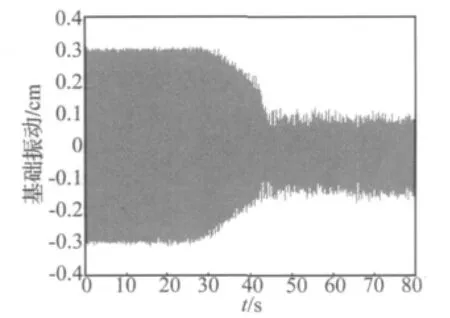
图14 连续惩罚抗饱和算法Fig.14 Experimental results of continuous punished algorithm

由实验结果知，限幅抗饱和算法与Rafaely抗饱和算法在磁悬浮主动隔振器的减振过程中出现不稳定现象，最终导致系统失控。这是因为限幅抗饱和LMS算法虽然可以达到绝对的饱和，但误差信号会产生各种倍频信号，最终导致减振系统的共振，从而使控制效果恶化。Rafaely抗饱和算法由于无法确定预量的大小，按照文献［1］中将q值设为饱和值是达不到很好的抗饱和效果，同时因为代价函数为分段函数，所以减振系统输出的误差信号中存在其它的倍频信号，引起减振系统的共振。而连续惩罚函数抗饱和算法在达到很好的抗饱和性的同时，由于代价函数为连续函数，减振系统输出的误差信号中其它倍频信号幅值很小，不会引起减振系统的共振。因此这种方法在达到抗饱和效果的同时取得很好的减振效果。

5 结论

本文对在饱和约束条件下的减振控制问题进行了研究，针对Rafaely等提出的抗饱和算法LMS算法进行了改进，并在磁悬浮隔振器上进行振动主动控制实验，通过三种抗饱和算法实验对比研究，结果表明，本文提出的改进算法能够在达到抗饱和性能的基础上依然有很好的减振效果。

［1］Rafaely F B，Elliott S J.A computationally efficient frequencydomain LMS algorithm with constraints on the adaptive［J］.IEEE Transactions on Signal Processing，2000，6:1649 －1655.

［2］梁 青，段小帅，陈绍青，等.基于滤波x-LMS算法的磁悬浮隔振器控制研究［J］.振动与冲击，2010，29(7):201 －203.

［3］吴 风，王景成，方小生，等.抗饱和控制的一些新进展［J］.化工自动化及仪表，2007，2:1－6.

［4］Alameda-Hernandez E，Blanco D，Ruiz D P，et al.The averaged overdetermined and generalized LMS algorithm［J］.IEEE Transactions On Signal Processing，2007，12:5593 －5603.

［5］尹建民，周雅莉，张 奇，等.考虑约束的频域算法在有源噪声控制中的应用［J］.噪声与振动控制，2004，3:18－21.

［6］孟令雷，倪向贵，王 永，等.基于MTS809的磁悬浮隔振器电磁力测量［J］.自动化与仪表，2009，3:4 －7.

［7］Vicen-Bueno R，Martinez-Leira A，Gil-Pita R，et al.Acoustic feedback reduction based on filtered-x LMS and normalized filtered-x LMS algorithms in digital hearing aids based on wola filterbank［J］.IEEE International Symposium on Intelligent Signal Processing，2007:1 －6.