智能结构振动同位配置控制中的局部应变研究

马天兵，杜 菲，吴义鹏

(1.安徽理工大学 机械工程学院，淮南 232001;2.南京航空航天大学 机械结构力学及控制国家重点实验室，南京 210016)

压电材料因具有响应速度快、良好的机电耦合特性被广泛应用于结构的振动与噪声控制中［1］。目前已有文献报道在压电智能梁结构自感自［2－3］或同位配置控制［4－5］中，压电传感片除感应基体的弯曲应变外还受到作动器诱导的拉压应变，而往往振动主动控制中需要使用压电传感片反馈信号，这种局部应变(拉压应变)的存在一定程度上削弱了控制效果。但在目前的智能结构振动主动控制研究中，局部应变的研究报道很少，特别是比梁更复杂的结构中，这一现象并没有引起足够的重视，关于压电板壳结构的局部应变研究国内外未见报道。

为进一步验证局部应变的存在和对控制效果的影响，本文运用ANSYS建立粘贴了压电片的板结构分析模型，针对结构的第二阶模态进行了谐响应分析，比较了同位激励和非同位激励情况下的各压电片的幅值与相位响应，理论上阐述了局部应变的存在。最后通过方波激励和MCS(Minimal Control Synthesis)算法在飞机壁板上进行了实验验证，为后续的局部应变补偿研究奠定基础。

1 局部应变理论

压电智能结构同位配置振动主动控制原理如图1所示。传感元件反馈信号到控制器，并由控制器产生合适的控制力，通过功放激励驱动元件，驱动力通过基体的厚度方向传播到传感元件上，从而导致压电传感元件的输出信号并不是单纯的弯曲应变响应，而是弯曲应变和拉压局部应变的耦合。

其中 εa，εs，εf和 εe分别为驱动元件的应变、传感元件的应变、弯曲应变和拉压局部应变。压电元件输出的电压值正比于响应应变，即:

其中us，uf和ue分别是传感电压、弯曲应变产生的电压和局部应变产生的电压。很明显ue的存在会直接影响到反馈控制的精度，因此有必要研究局部应变在二维固支板结构振动控制中的影响。考虑到第一阶模态最大应变在板中心，只能粘贴一对压电片，传感片只有一个，不方便谐响应分析比较。本文选择如图2所示板结构的第二阶模态来进行研究，因为此模态下两个应变最大位置为(0.25a，0.5b)和(0.75a，0.5b)处(其中a和b分别为板的长度与宽度)，如果分别粘贴一对压电片，这四个位置在第二阶频率激励下，幅值大小理论上应基本相等，便于比较。

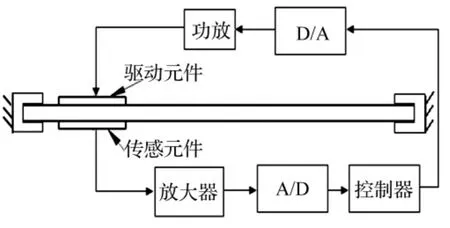
图1 智能结构控制原理图Fig.1 The control principle diagram of smart structure

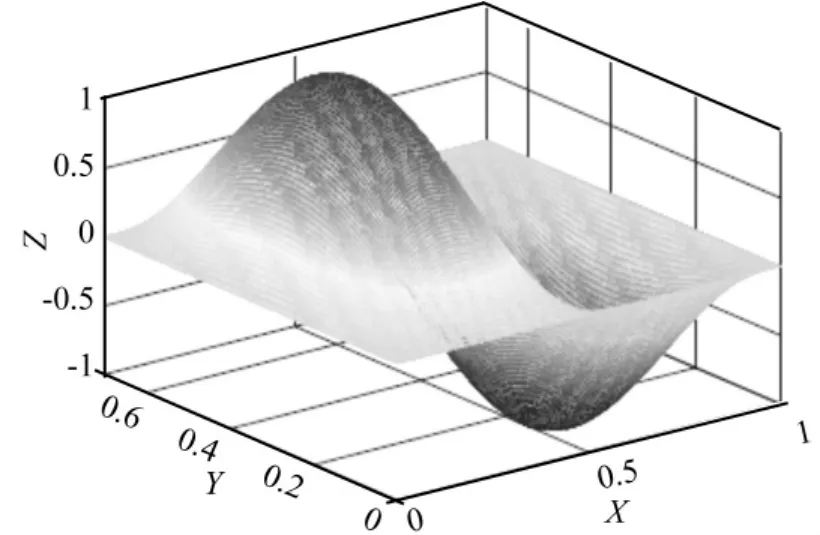
图2 固支板第二阶模态振型Fig.2 The second order modal shape of fixed supported plate

2 模型仿真与分析

2.1 ANSYS建模

在 ANSYS12.0软件［6］中，建立粘贴了压电片的四边固支板模型。其中压电片选用PZT8，具体参数如表1表2所示。压电片单元选择SOLID5，且令KEYOPT(1)=3。压电片单元采用映射网格划分，将单元划分成为六面体单元，长和宽均为10 mm。板材料选用铝，单元选择SHELL63，采用映射四边形单元划分，尺寸设置为20 mm。划分网络并施加约束后如图3所示，先前设计考虑前三阶模态，所以粘贴了5对压电片，标注的数字表示当前面上的压电片和反面的压电片(括号里标注的数字)。

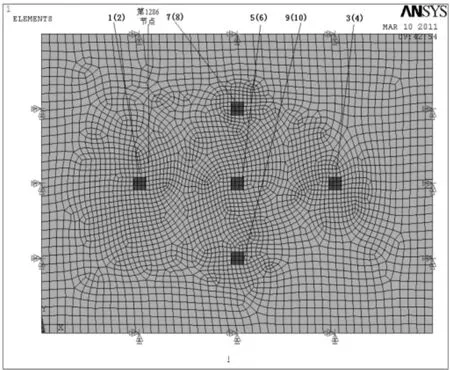
图3 压电板结构仿真模型Fig.3 The simulation model of piezoelectric plate

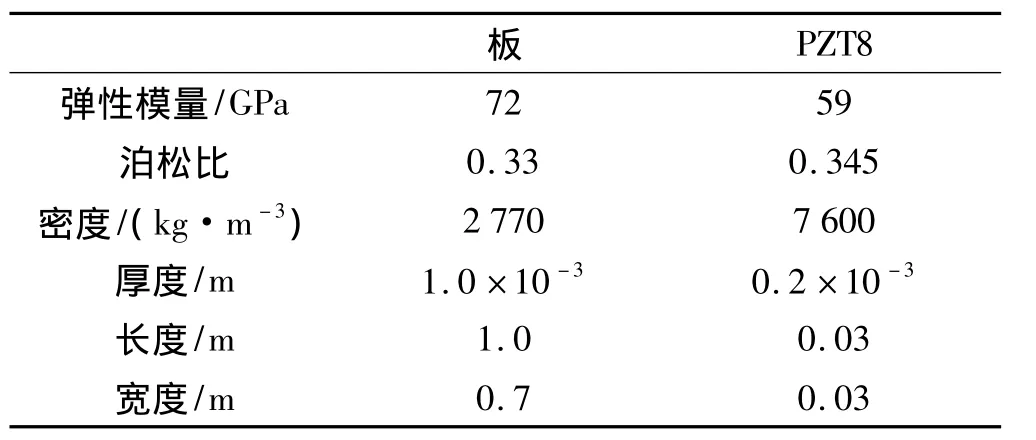
表1 压电板结构的材料和几何参数Tab.1 The material and geometric parameters of piezoelectric plate

表2 PZT8的材料参数Tab.2 The material parameters of PZT8

2.2 仿真结果与分析

首先对结构采用模态分析，为下一步的谐响应分析确定频率范围，减小谐响应分析的计算量。通过ANSYS模态分析，得到图4图5中结构的第二、三阶固有振型，与实际的振型基本吻合。

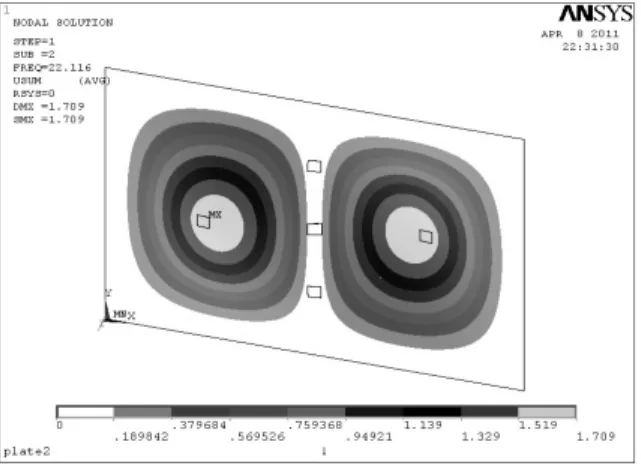
图4 第二阶振型Fig.4 The second order modal shape

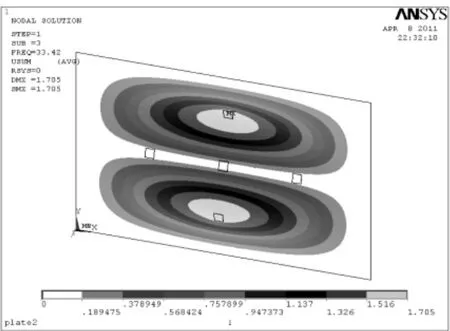
图5 第三阶振型Fig.5 The third order modal shape

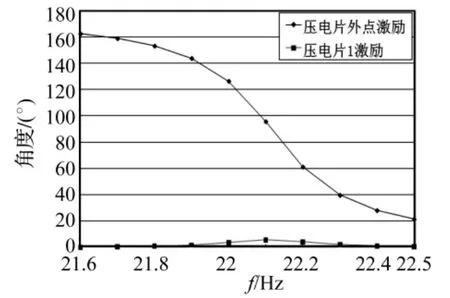
图6 不同点激励下压电片2的相位响应Fig.6 The phase response of PZT2 under different excitation

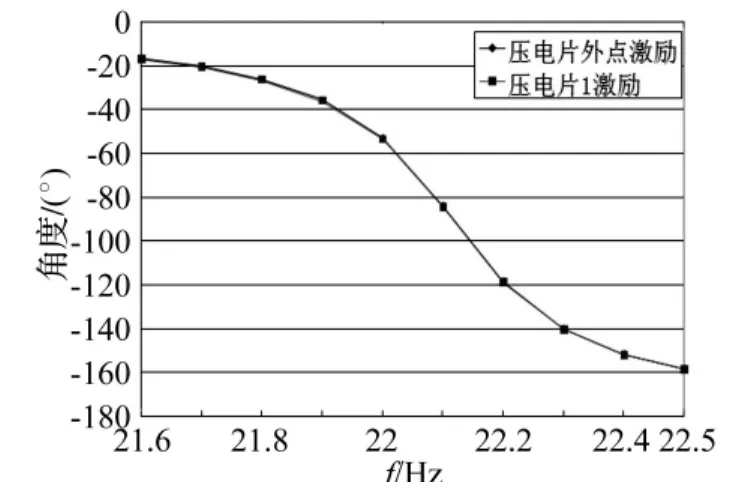
图7 不同点激励下压电片3的相位响应Fig.7 The phase response of PZT3 under different excitation

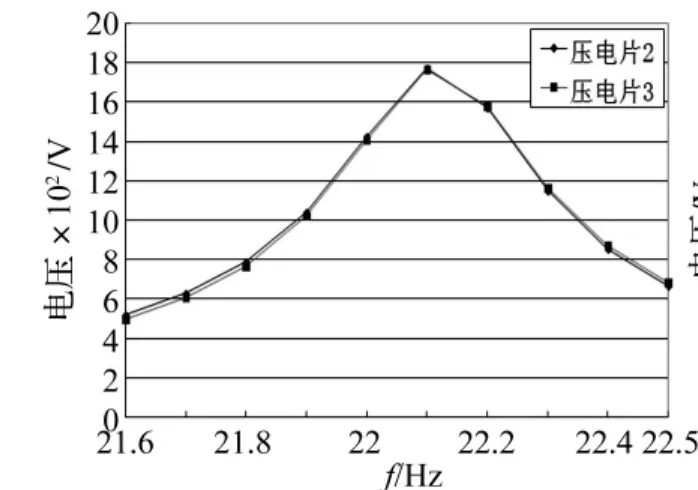
图8 外点激励下压电片2、3的幅值响应Fig.8 The amplitude response of PZT2 and PZT3 under outside excitation of PZT

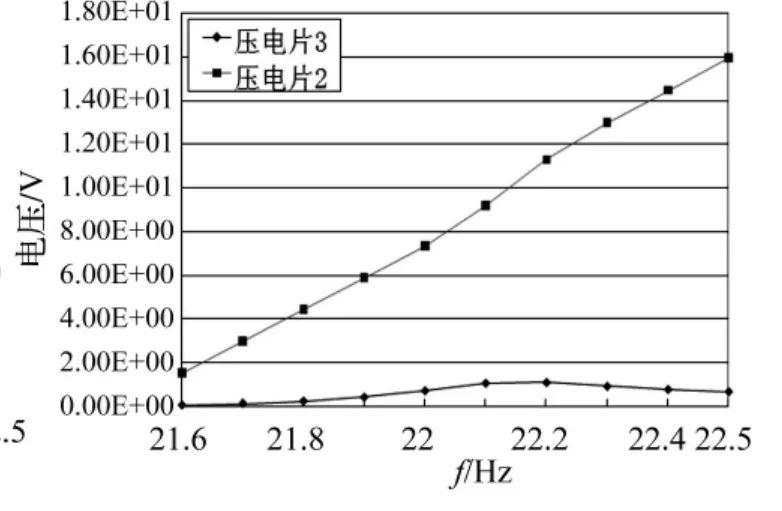
图9 压电片1下激励压电片2、3幅值响应Fig.9 The amplitude response of PZT2 and PZT3 under PZT1 excitation

对结构采用谐响应分析，限于篇幅仅选择左右对称的压电片来考虑，上下对称的压电片(第三阶模态)可采取下述同样的分析方法。根据图4所示，第二阶模态频率为22.116 Hz。采取两种激励方法，一是选取压电片外的如图3所示的第1286节点处施加幅值为100 N的力，另一是在压电片1的上表面施加幅值为200 V的正弦电压，各压电片与板粘贴的电极面设置为0 V，正弦控制电压的频率变化范围设为21.6～22.5 Hz，子步设置为10，结构阻尼比设置成0.007。比较不同压电片在不同激励情况下的响应，仿真结果如图6～图9所示。采用片外点激励时，在第二阶模态处左右对称压电片2，3幅值响应基本相同，由于是柔性薄板导致理论上响应幅值很大，压电片2的相位是90°，压电片3是－90°，相位差180°，在不同点激励压电片3的相位基本上无变化，这与实际是吻合的。但是在压电片1激励时，压电片1对称的反面压电片2相位和幅值都发生很大变化，幅值远大于右边压电片3，而且超过第二阶模态频率后压电片2幅值并没有衰减，甚至呈现增大趋势，主要因为对于柔性结构拉压振动的固有频率比低频弯曲振动频带高的多，而且压电片2的相位也发生根本性改变，这正是由于驱动压电片1使得结构发生小范围的局部变形，使得同位粘贴的压电片2不仅包含了结构共振的弯曲应变量，而且包含了局部应变量。

3 局部应变的实验验证

为了验证局部应变的存在，本文以实验室的飞机壁板为研究对象，搭建图10所示的实验系统，运用DSPACE1103作为控制器，铝合金材料为壁板材料，在板的中点放置激光位移传感器来测量板的振动位移，在中心点正反两面各贴上一块压电片。DSPACE系统产生激励电压，并由功放驱动作动器，从而使壁板产生振动，施加不同策略，通过比较压电传感元件上感应到的电压和位移传感器响应来阐述局部应变的存在和影响。

3.1 方波激励实验

在压电驱动元件(反面中心点的压电片)上施加频率为307.7 Hz的方波激励信号，该频率也是通过实验扫频得出壁板结构的第一阶模态频率。选择方波信号的主要原因在于该信号是多种频率成份正弦信号的叠加，且除了307.7 Hz之外，其他的奇倍频成份对板的一阶模态影响可忽略不计。如果压电传感元件(正面中心点的压电片)只感应板的振动模态，则其感应到的信号在频谱分析中有且只有一个谱峰，频率为307.7 Hz。如果压电传感元件受到了驱动元件局部应变的影响，则其感应到的信号在频谱分析中就会出现多个谱峰。

结合图11可知，压电传感元件感应到的信号明显带有方波的成分，频谱上出现了3倍频等的奇次谐波成分，可见其受到了压电驱动器上信号的影响。激光位移传感器感应到的电压信号是一个正弦信号，它正确地反映了固支壁板的第一阶振动模态是频率为307.7 Hz正弦振动，在3倍频处出现一个很小的峰值，这是因为实验中选择的传感片的中点粘贴了反光纸，局部应变对垂直振动方向有极其微小的影响。可见如果用压电片感应的电压信号来作为控制系统的反馈，将会有较大的误差。

3.2 MCS算法控制实验

MCS算法具有在系统参数变化、外部干扰、系统内部动力耦合与系统非线形的情况下也能达到优良的闭环性能的优点［7］，已被应用于智能结构振动主动控制中［8］。为了验证局部应变对主动控制的影响，实验中选用壁板内面上方的压电片施加频率为307.7 Hz的正弦波作为激励，内面中点的压电片做控制，外面中点压电片做传感，并作为算法的反馈，激光位移传感器测量中心点位移，得到了控制前后不同传感元件的响应。

图10 壁板振动控制实验照片Fig.10 The experiment photo of aircraft panel vibration control

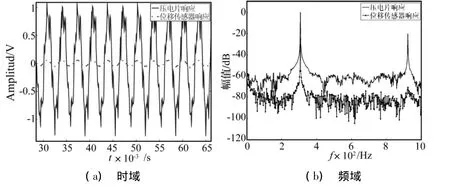
图11 方波激励下传感元件的响应Fig.11 The sensor time domain and frequency response under square wave excitaion

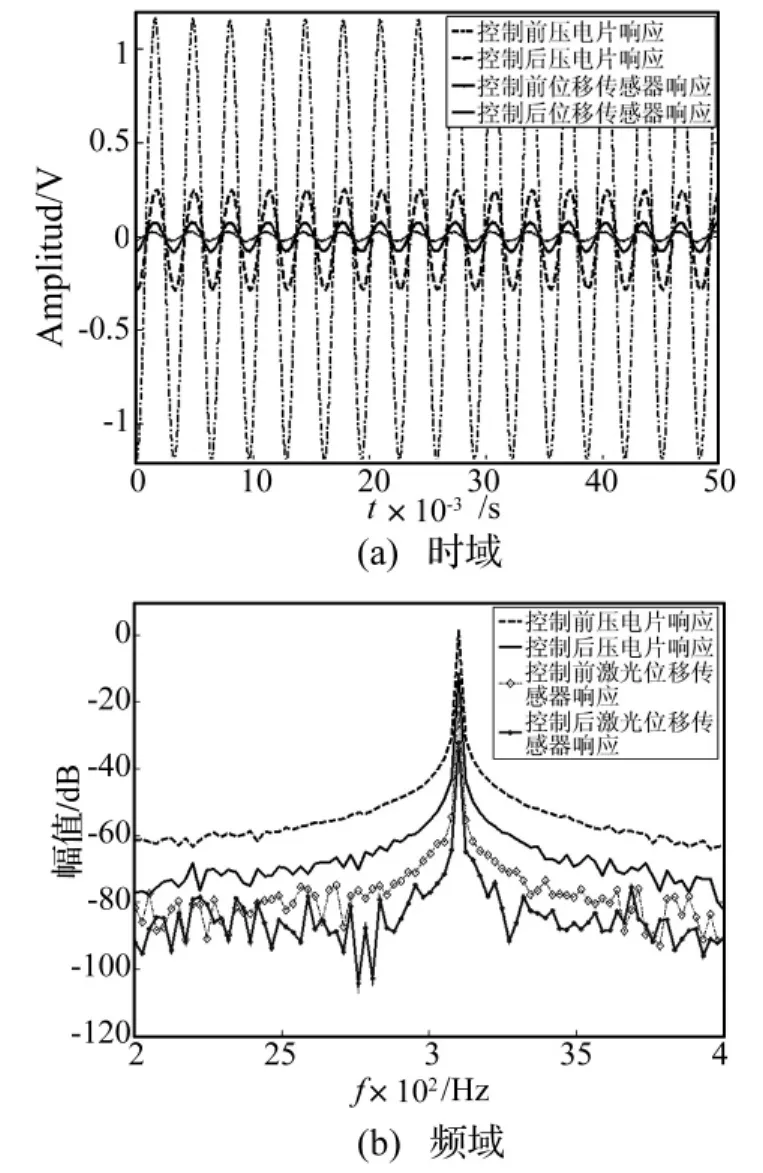
图12 MCS控制下传感元件的响应Fig.12 The sensor time domain and frequency response under MCS algorithm control

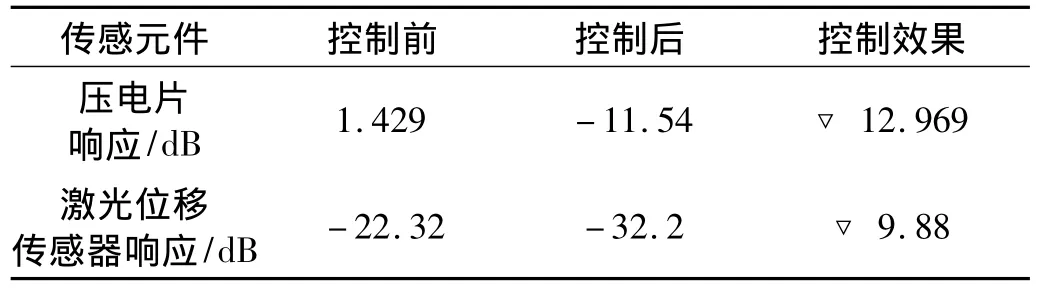
表3 传感元件响应效果比较Tab.3 Comparation of the sensor response

通过图12和表3可知MCS算法在壁板的振动控制中有较好的效果。实验中采用两种不同的度量方式传感器，激光位移传感器测量值线性反映结构的振动位移，而压电传感片电压值直接反映的是长度方向的应变［9］，由于同位配置中压电片响应耦合了局部应变，既有弯曲应变又有拉压应变，导致在本次实验中压电片反映的控制效果较好。但是理论上在同一位置两种方案应该有相近的控制效果，表3显示的差异在一定程度上验证了局部应变的存在及其对控制效果的影响。

4 结论

本文通过ANSYS对板结构进行了谐响应分析，比较了不同点激励下对称压电片的幅值与相位响应，实验中通过了方波激励和MCS主动控制，比较了不同传感元件的响应，充分证明了局部应变在压电智能板结构振动同位配置控制中的存在，为下一步局部应变的补偿研究和进一步提高主动控制效果奠定良好的基础。

［1］陶宝祺.智能材料结构［M］.北京:国防工业出版社，1997.

［2］Ji H L，Qiu J H，Wu Y P，et al.Novel approach of self-sensing actuation for active vibration control［J］.Journal of Intelligent Material Systems and Structures，2011，7(1):1 －11.

［3］Gibbs G P，Fuller C R.Excitation of thin beams using asymmetric piezoelectric actuators［J］.J Acoust Soc Am，1992，92(6):3221－3227.

［4］Crawley E F，Anderson E H.Detailed models of piezoceramic actuation of beams［J］.Journal of Intelligent Material Systems and Structures，1990，1(1):4 －25.

［5］姚 军，李岳峰，朱德懋，等.电子阻尼的增进—局部激励应变的补偿［J］.航空学报，1998，19(4):400 －404.

［6］刘 伟，高维成，于广滨，等.ANSYS 12.0宝典［M］.北京:电子工业出版社，2010.

［7］陈复扬，姜 斌.自适应控制与应用［M］.北京:国防工业出版社，2009:305－309.

［8］Ma T B.Multimode vibration supression of piezoele-ctric plate based on minimalcontrol synthesis algorithm［C］.Cecnet2011，2011，4:2351 －2354.

［9］田海民.智能悬臂梁的振动控制及其优化配置［D］.兰州:兰州理工大学，2008:19－21.