基于正交化HHT和随机相位模拟非平稳随机过程

胡灿阳，陈清军，祁 冰，徐庆阳

(1.南京审计学院 江苏省公共工程审计重点实验室，南京 210029;2.同济大学 土木工程防灾国家重点实验室，上海 200092;3.河南省建筑科学研究院有限公司，郑州 450053)

现实生活中的很多非平稳随机过程，不仅强度是非平稳的，而且频率含量也是非平稳的。在地震波分析、地铁和车辆振动分析、海浪资料分析、风的分析等很多领域里都需要模拟非平稳过程。罗雄等［1］利用观测的风速记录，通过快速傅氏变换和希尔伯特变换，建立了非平稳随机过程模型。李锦华等［2］利用推导出的调制函数，运用谐波合成法模拟的非平稳脉动风速，具有强度和频率的双非平稳性，但是模拟计算量非常大，不具有普遍适用性。Yeh等［3］通过频率调制的随机过程乘以确定的时变函数来表达非平稳地震动过程。但是它使用穿零率方法来进行频率调制函数的参数估计，并且频率调制过程独立于强度调制，这就使这个模型存在某些限制，只适用于一些特定类型的随机过程。Liang等［4］基于Priestley演变谱理论，推导了模拟一维单变量非平稳随机过程公式，并模拟了非平稳地震动过程。王国林等［5］对四轮相关车辆非平稳路面激励的时域模型进行了建模和仿真，从而可以作为路面输入为进一步研究提供参考。

从上面可以看到，在很多研究领域都需要非平稳过程的仿真以作为研究的输入激励，但在以往的研究中，人们大都把注意力放在幅值谱上，对相位谱的研究却很少。这主要是因为相位谱要比幅值谱不规则得多［6］。时程所包含的相位特性对这两个非平稳性都有很大影响。大崎顺彦等［7］较早地强调了地震动相位信息在模拟强地震动的重要性。本文即通过正交化HHT方法和考虑随机过程的相位［8］来进行非平稳随机过程的模拟。

1 正交HHT变换

Huang等［9］提出了 Hilbert-Huang 变换(HHT)，这种方法特别适合非平稳信号的分析和处理。然而在实际应用中发现，文献［9］给出的EMD分解得到的IMF分量之间不是完全正交的。由图1可见，通过传统的HHT变换进行非平稳地震地面运动谱密度估计时，会存在能量泄漏，EI Centro波的能量泄漏高达40%［10］。楼梦麟等［11］给出了正交化的EMD分解方法，这样就很好的解决了EMD分解的问题，使各IMF分量之间是严格正交的。

通过正交化处理后，从EMD分解得到时程信号X(t)有如下分解形式:

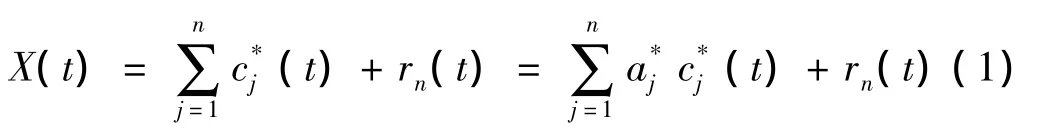
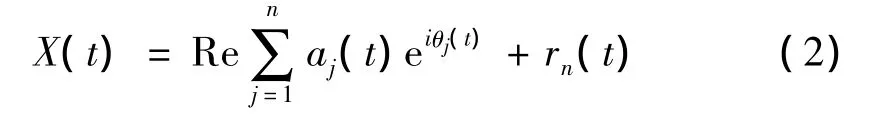
aj(t)和 θj(t)分别为j阶信号的瞬时幅值和瞬时相位，由下式计算:

把信号振幅显示在频率－时间平面上，就可以得到Hilbert幅值谱 H(ω，t)，称为 Hilbert谱，记作:

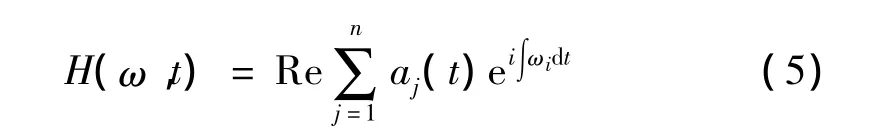
图1给出了EI Centro地震地面记录、Taft地震地面记录和Kobe地震地面记录，分别采用正交化HHT法(OHHT)和文献［9］的HHT法所估计的地震波局部谱密度的能量归一化Husid图［12］。

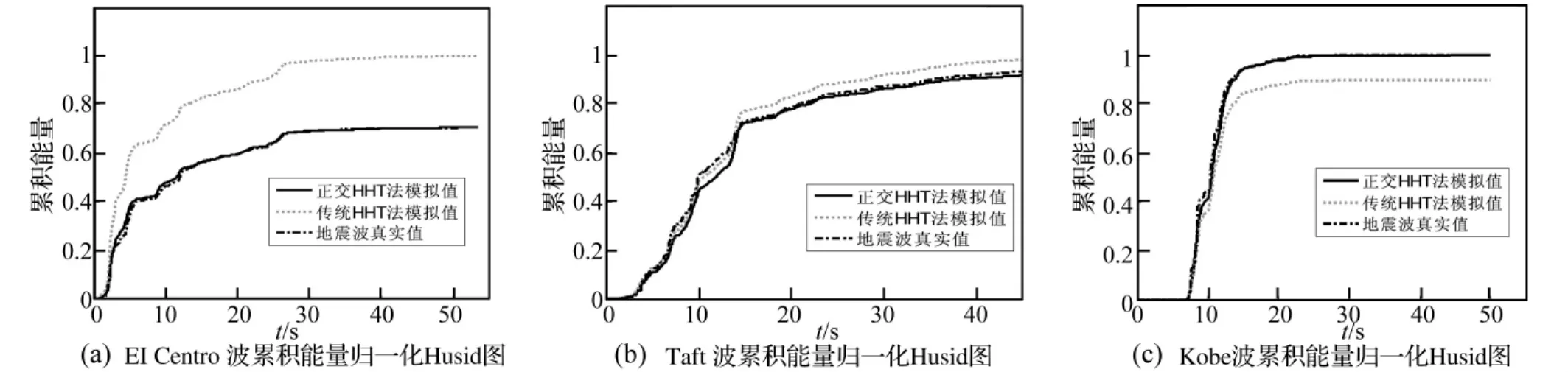
图1 OHHT和HHT估计的地震波能量归一化Husid图Fig.1 Unitary Husid curve of seismic wave energy estimated by OHHT and HHT

由图1可见，无论能量变化过程还是总能量，OHHT的Husid图都和真实地震记录完全吻合，说明利用正交化HHT法来估计地震波的局部谱密度具有极高的精度。图1中的三个地震波的OHHT法不存在能量泄漏，而用HHT法时，三个地震波的能量均有泄漏情况。其中，EI Centro波的能量泄漏高达30%。

由此可知，由正交HHT法得到的Hilbert谱比传统HHT的Hilbert谱具有更高的精度，更能反映非平稳随机过程的时－频特性。

2 非平稳过程的生成及统计特性研究

在工程中，一些实际物理过程不能通过数学方法来精确处理，这就要对它建立一个理论模型进行分析。主要是通过观测的数据来建立随机过程模型，观测的记录可作为随机过程的一个样本。基于正交HHT方法的Hilbert谱能够精确描述这一样本幅值和频率成分随时间的变化。不同样本的Hilbert谱是不同的，因此，随机过程的Hilbert谱可以认为是所有样本的Hilbert谱的期望值:

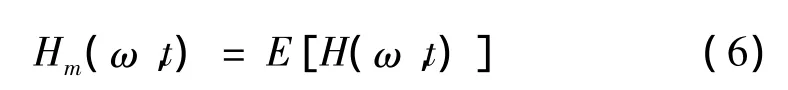
然而，实际情况是有些随机过程，比如地震这样的随机过程往往只能记录到一个样本，这时，对于随机过程统计特性的分析和随机过程的模拟都是困难的。在这种情况下，只能基于工程实际来作出一些假定才能对随机过程进行分析。在建立非平稳随机过程的模型时，参数估计是一个非常重要却又容易出问题的环节。本文假定，已知样本基于正交HHT方法得到的Hilbert谱即为随机过程的Hilbert谱，这样虽和实际情况可能还有一些偏差，但它不再需要假设和进一步的近似分析，是一种便于实现的方法。

从式(1)、式(5)看出，基于Hilbert谱可以通过引入一个随机变量φj来构建随机过程:

其中，φj是独立的相位角，它服从于［0，2π］均匀分布，这样X(t)就成为一个随机过程，其均值、协方差和方差分别是:

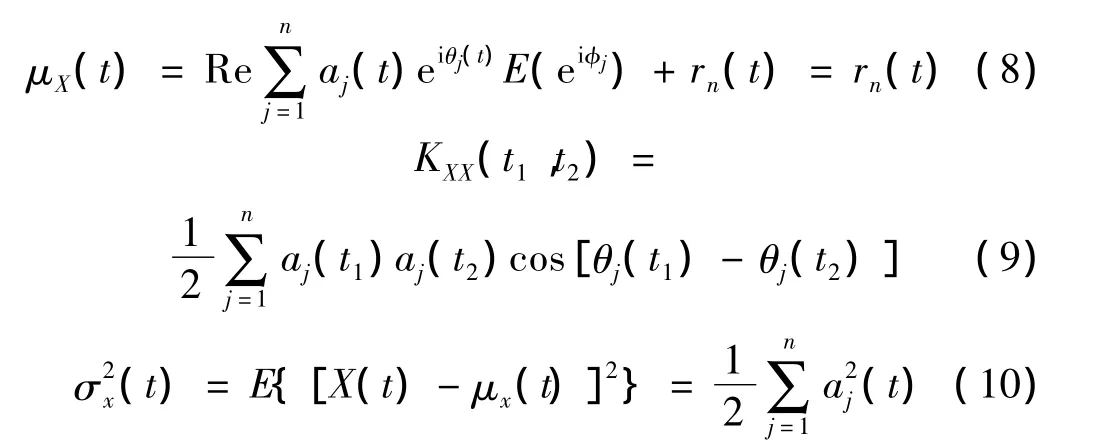
根据中心极限定理，当n足够大时，X(t)趋于高斯分布。式(7)是通过Hilbert变换后生成的随机过程，它的m个样本函数组成样本空间［X1(t)，X2(t)，…，Xm(t)］。其中第k个样本是:

第三，通过完善“互联网+”的建设，使基础信息数据具有整合性的特质，从而保证数据的方向型传输。进而使数据的收集、数据的运用、数据的储存能在校园数据库中进行整合、分析和处理。特别是需要根据“互联网+”的功能分层做出相应调研，使教学、管理和信息的传递功能不会因数据的混乱而造成整合发生偏差。

它的均值、协方差和方差可以由式(8)～式(10)求得。可见，Hilbert谱可以方便的表示任一样本的幅值函数和瞬时频率。第p个和第q个样本的互协方差函数为:

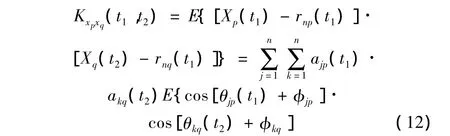
从上式可以看出，协方差函数依赖于各样本正交IMF分量的幅值、相位函数和随机相位偏移。比如，若两个样本的随机相位角在统计意义上独立于所有的φjp和φkq，那么互协方差函数为零。如果两个样本之间的相位偏移具有相关性，则可以建立它们的互协方差函数。可以使两个样本的相位偏移具有某种函数关系。比如可以给出两个样本同阶IMF分量的相位偏移关系:

其中，(j=1，2，…，n，q=2，3，…，m)，ψjq是常数。这样，不同样本的同阶IMF分量的随机相位偏移之间是相关的，但不同阶IMF分量的随机相位偏移是独立的。当 φj1为［0，2π］间的均匀分布时，φjq则服从于［－ψjq，2π－ψjq］上均匀分布，它的分布范围仍然在2π之内。均值、协方差和方差仍由式(8)～式(10)给出。两个样本信号间的互协方差为:

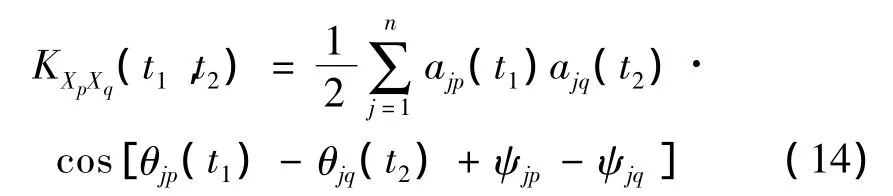
由上式可见，互协方差依赖于不同样本的同阶IMF分量幅值的乘积，也和这些IMF分量的相位差与随机相位偏移差之和相关。当这两个差值之和非常小时，余弦函数接近1，这时，两个样本的互协方差只与IMF分量的参数有关。当总差值接近于π/2时，互协方差为零。在实测的基础上，调整常数项 ψjq可以给建立互协方差函数带来一定的灵活性。在确定的物理机制下，可以假定所有样本之间的随机相位偏移一致，那么样本之间的关系符合式(14)，并且 ψjp=ψjq=0。

上面给出了描述随机过程各样本之间相关性的一种方法，通过正交IMF分量的Hilbert谱来估计协方差函数。由式(7)可以看出，通过Hilbert谱分析模型可以很方便地进行非平稳过程的仿真，在式(7)中，改变随机相位角可以得到随机过程的样本函数。模拟样本的Hilbert谱均值和目标Hilbet谱是一致的。样本平均值也和目标值相一致，因此，符合模拟标准。同时，也推导出用已知样本Hilbert谱参数表示的模拟非平稳随机过程的统计特性函数，便于实际分析和应用。

3 算例验证

基于EI Centro地震记录和地铁振动记录的样本Hilbert谱进行数字仿真，来验证上述方法的正确性。表1～表4分别给出了EI Centro南北向地震地表记录和上海地铁1号线常熟路站的一个实测地表振动记录时程和9个样本时程的均值和方差。可以看出模拟样本的均值和方差都与原记录很接近，特别是地铁振动样本与记录的方差完全一致，说明模拟样本对均值的分散程度很好。

表1 EI Centro记录和模拟样本的均值Tab.1 Recorded and simlulated El Centro arithmetic average

表2 EI Centro记录和模拟样本的方差Tab.2 Recorded and simlulated El Centro variance

表3 地铁振动记录和模拟样本的均值Tab.3 Recorded and simlulated subway vibration arithmetic average

表4 地铁振动记录和模拟样本的方差Tab.4 Recorded and simlulated subway vibration variance

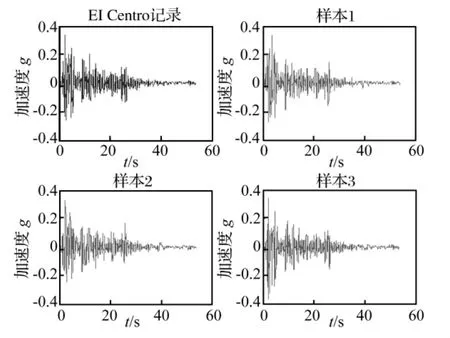
图2 EI Centro记录和模拟样本Fig.2 Recorded and simlulated EI Centro

图3 地铁振动记录和模拟样本Fig.3 Recorded and simlulated subway vibration

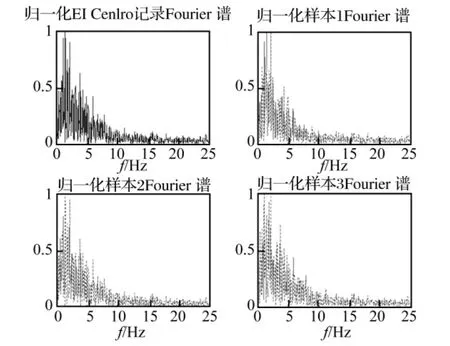
图4 El Centro记录和模拟样本的傅里叶谱Fig.4 Fourier spectra of EI Centro record and its samples

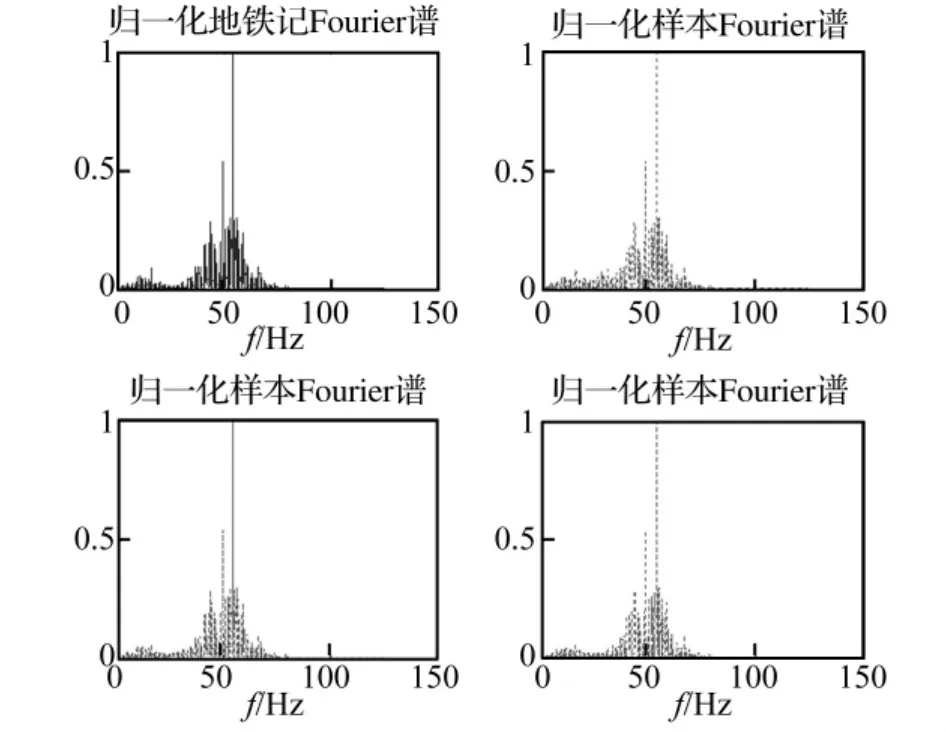
图5 地铁振动记录和模拟样本的傅里叶谱Fig.5 Fourier spectra of subway vibration record and its samples

图4、图5是原记录和样本的傅里叶谱。可以看出，无论是以低频为主的地震动还是高频的地铁振动，每种情况的三个样本频率分布情况和原记录都非常相符。因此，基于正交Hilbert谱产生的样本也能够很好的反映非平稳随机过程的频率变化特性。

为了更加清楚地对比模拟样本与原记录的时频特性，图6、图7分别给出了地震记录与地铁振动记录及样本的小波时频分布图。利用Morlet小波对原记录和相应样本进行小波分解，得到能准确反映它们时频非平稳特性的局部谱。由图可见，利用本文方法模拟生成的非平稳随机过程样本的时频特性都和原记录非常符合。

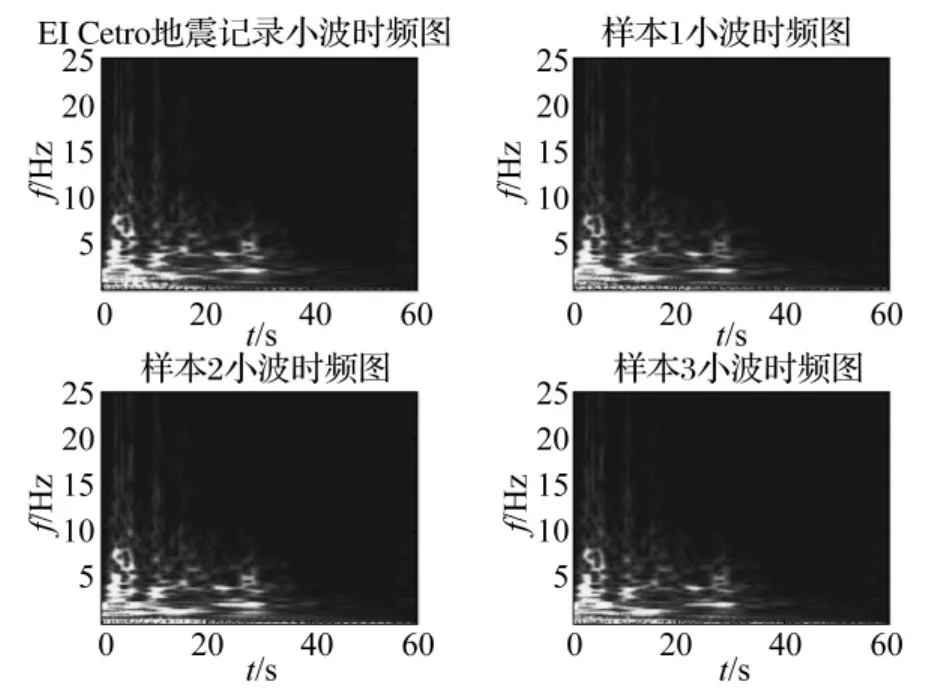
图6 EI Centro记录和模拟样本的小波时频分布Fig.6 Wavelet time-frequency distribution of EI Centro record and its samples

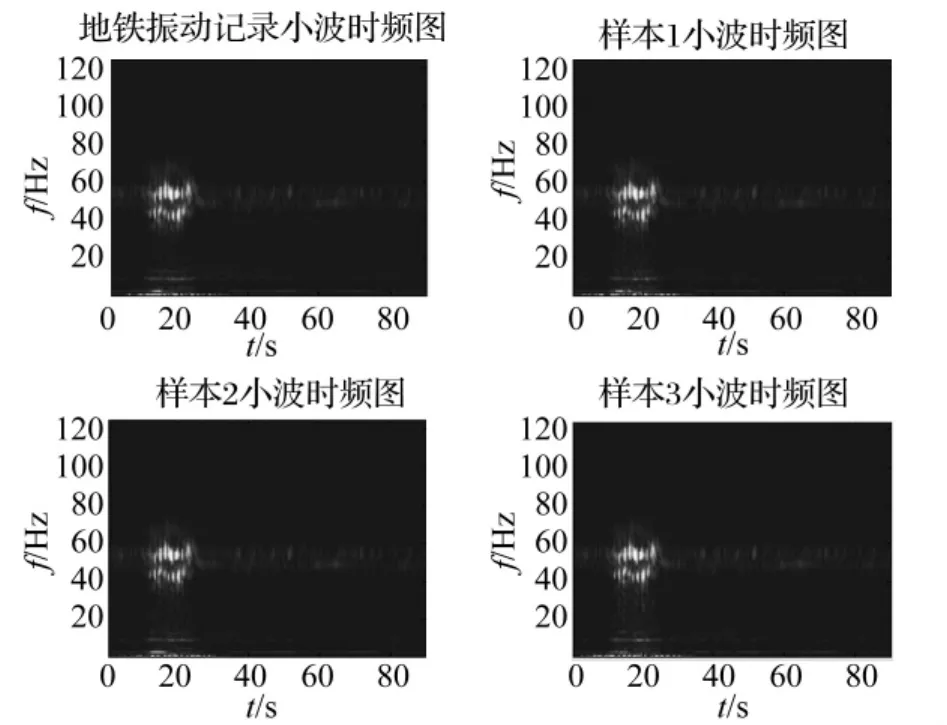
图7 地铁振动记录和模拟样本的小波时频分布Fig.7 Wavelet time-frequency distribution of subway vibration record and its samples

图8给出了El Centro记录和四个样本的加速度反应谱，反映出模拟样本的加速度反应谱和原记录的加速度反应谱变化趋势相一致。

图8 El Centro记录和模拟样本的加速度反应谱Fig.8 Acceleration response spectra of El Centro ground motion record and simulations

4 结论

由于正交HHT变换克服了传统HHT变换存在能量泄漏的缺点，它可以作为一种对非平稳信号进行时频分析的精确方法。可以通过正交HHT变换得到的Hilbert谱进行非平稳随机过程的模拟。首先通过正交化EMD分解，进而进行Hilbert变换，得到瞬时频率和幅值，在此基础上进行非平稳随机过程的模拟。这样就克服了目前常用的频率调制或者频率、幅值双调制存在的困难与不足。并且给出了非平稳随机过程的均值、方差和协方差的Hilbert谱表示方法。本文的方法提取了非平稳随机过程自身的物理特性，在没有改变它的基础上进行了非平稳随机过程的仿真。既不需要假定一个函数作为目标谱，也不用进行分段平稳假设。文中给出了由样本Hilbert谱参数表示的模拟随机过程统计特性函数，具有很方便的使用性。并且通过算例验证了本文方法进行非平稳随机过程模拟在强度、频率和反应谱等方面都具有很高的精度，既适用于低频随机过程，也适用于高频随机过程的模拟。算例还表明:模拟计算速度很快，可以为进一步的研究提供大量非平稳随机过程样本，具有很好的适用性和使用性。

［1］罗 雄，李永乐.按非平稳随机过程模拟自然风速的一种数值方法［J］.西南交通大学学报，2002，37(4):367－370.

［2］李锦华，李春祥，申建红.非平稳脉动风速的数值模拟［J］.振动与冲击，2009，28(1):18－23.

［3］Yeh C H，Wen Y K.Model of nonstationary earthquake ground motion and application［C］.Proceedings of Fourth U.S.National Conference on Earthquake Engineering，1990，1:505－ 514.

［4］Liang J，Chaudhuri S R，Shinozuka M.Simulation of nonstationary stochastic processes by spectral representation［J］.J.Engrg Mech，ASCE，2007，133(6):616 －627.

［5］王国林，胡 蛟，钱金戈，等.路面对汽车非平稳激励的时域仿真及小波分析［J］.振动与冲击，2010，29(7):28－32.

［6］朱 昱，冯启民.地震加速度相位差谱分布的数字特征［J］.地震工程与工程振动，1993，13(2):30 －37.

［7］大崎顺彦著，吕敏申，谢礼立，译.地震动的谱分析入门［M］.北京:地震出版社，1980.

［8］金 星，廖振鹏.地震动相位特性的研究［J］.地震工程与工程振动，1993，13(1):7 －13.

［9］Huang N E，Shen Z，Long S R，et al.The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis ［J］.Proc.R.Soc.Lond.A，1998，454:903－995.

［10］胡灿阳，陈清军.非平稳地震地面运动局部谱密度正交化HHT估计［J］.同济大学学报(自然科学版)，2008，36(9):1164－1169.

［11］楼梦麟，黄天立.正交化经验模式分解方法［J］.同济大学学报(自然科学版)，2007，35(3):293 －298.

［12］Husid R L.Analisis de terremotos:analisis general［J］.Revista del ID1EM，Santiago Chile，1969，8(1):21－42.