矩形敞口水池壁板转角处的精细化设计

宋江

（中国市政工程中南设计研究总院有限公司 武汉430010）

引言

目前，对钢筋混凝土矩形敞口水池壁板的设计，一般都是参照《给水排水工程钢筋混凝土水池结构设计规程》（CECS 138：2002）［1］、《给水排水工程结构设计手册（第二版）》［2］进行。即首先对壁板进行内力计算，求得竖向和水平向最大内力后，然后在竖向和水平向均按求得的最大内力进行结构配筋，此方法用于工程实践是安全可靠的，但是没有考虑壁板转角处的局部受力特点，存在进一步优化设计的空间。

本文通过采用有限元软件对单块壁板转角处的受力进行分析，更加精确地了解池壁转角处内力分布和规律，从而更合理地指导工程设计。

1 精细化设计方案的提出

壁板通常采用长短筋搭配的配筋方式，如图1所示。

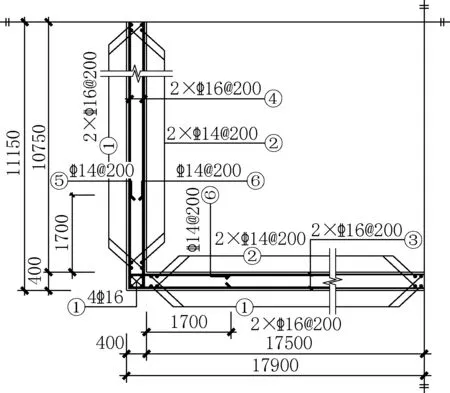
图1 常规长短筋搭配的配筋方式（单位：mm）Fig.1 The conventional reinforcement with long and short rebar（unit：mm）

壁板实际竖向弯矩可由有限元软件计算得到，假定以一块长20m、高8m的壁板为例，支座形式为三边固定顶端自由，在8m高的水压作用下的弯矩分布如图2所示，竖向弯矩在壁板根部的中间部位最大，其数值沿两边衰减，因此沿壁板长度方向全部采用长短筋搭配的配筋方式会造成一定的浪费。另外根据文献［1］条文6.1.3图（C）可知，壁板转角处的水平向弯矩沿竖向近似呈倒三角形分布，在壁板顶端最大，壁板底部为零。

图2 壁板实际竖向弯矩（单位：kN·m/m）Fig.2 The actual vertical bending moment of the wall panel（unit：kN·m/m）

实际工程中，考虑到节省造价，可采用如图3、图4所示的精细化配筋方式。

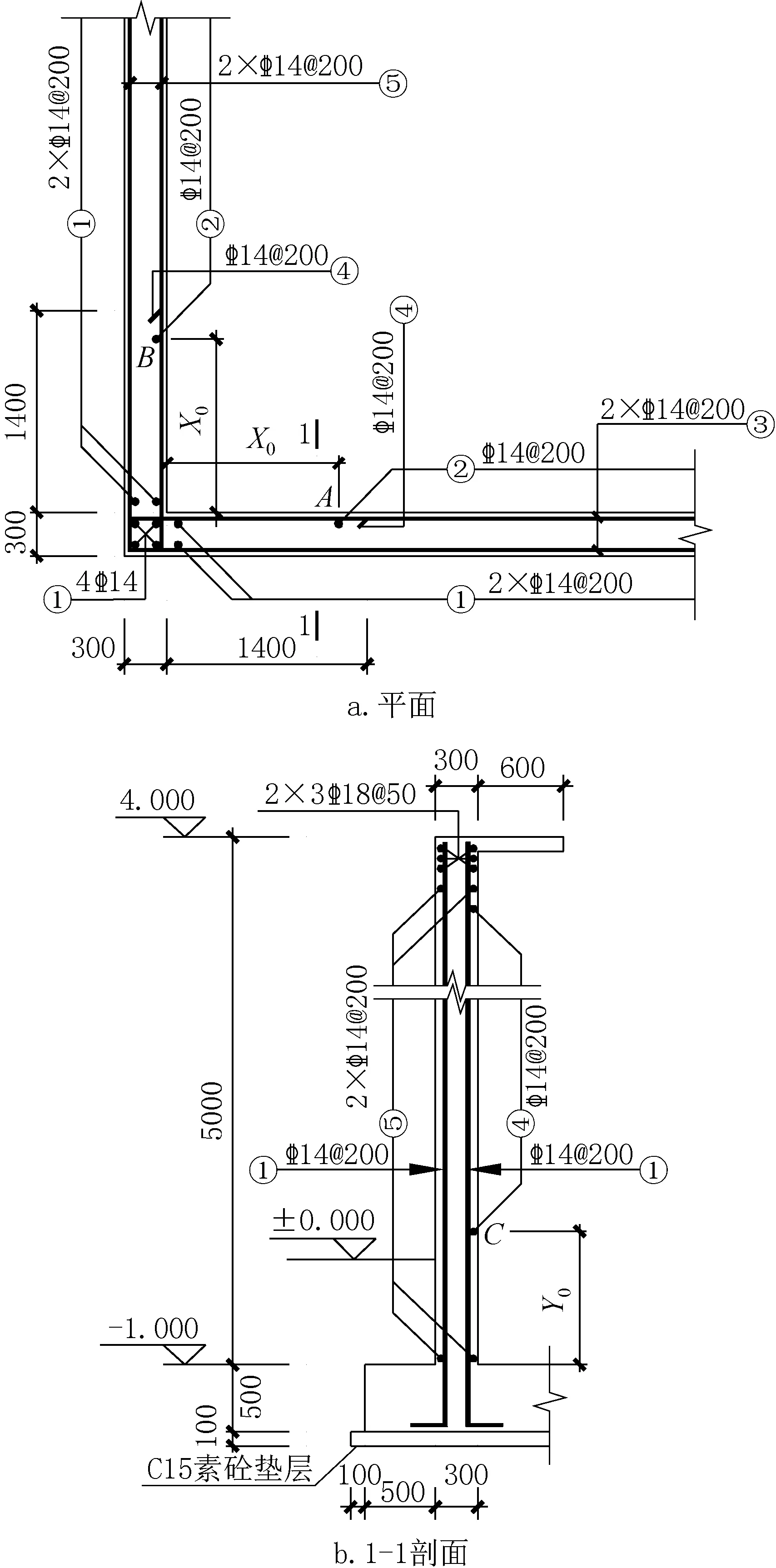
图3 壁板转角处平、剖面配筋大样（单位：mm）Fig.3 The plan and section of reinforcement of the wall panel corner（unit：mm）

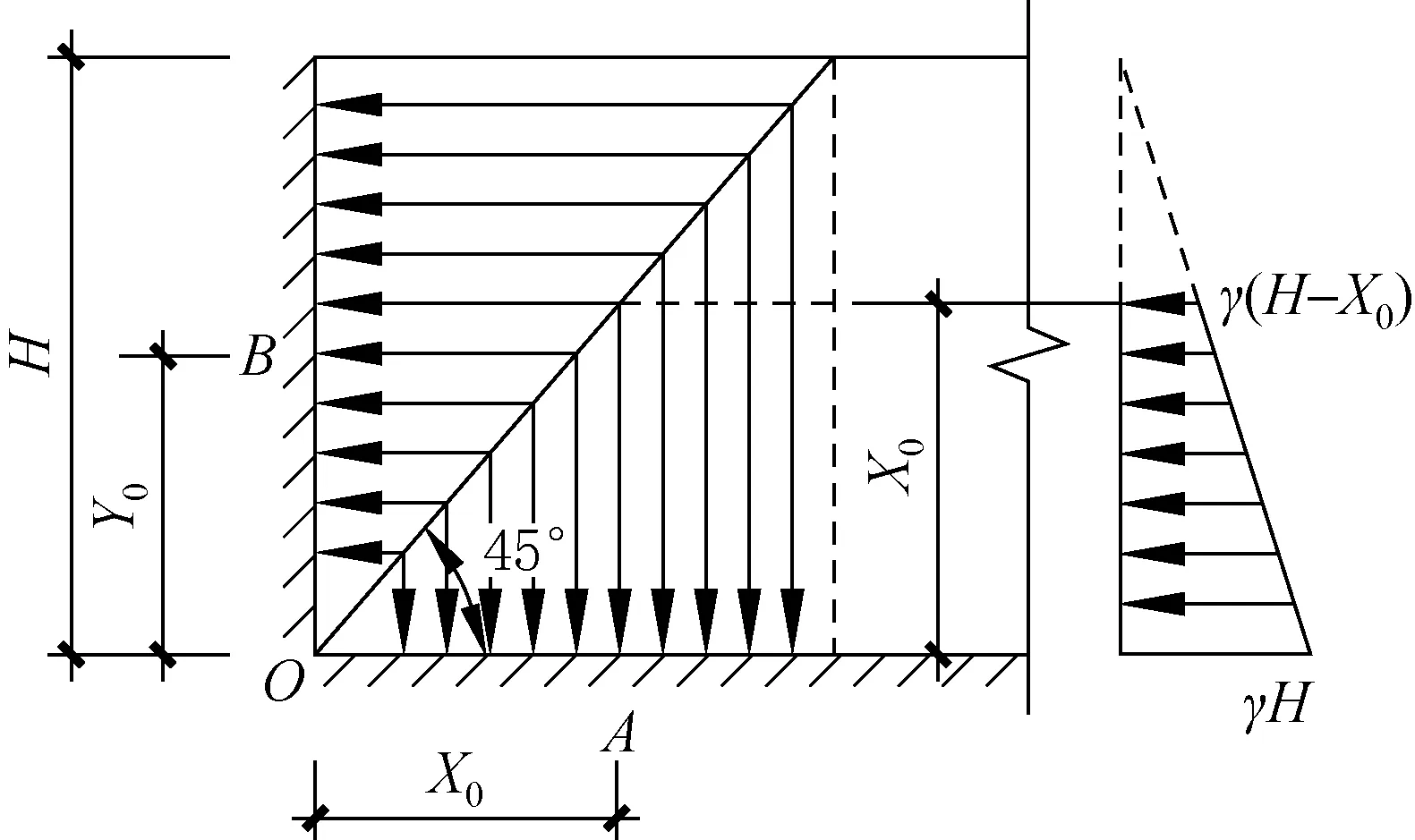
图4 壁板转角处满水荷载简图Fig.4 The diagram of water load of the wall panel corner

图3 a所示的A、B点及图3b所示的C点分别为竖向内力和水平向内力达到最大内力值一半所对应的点，其中标注尺寸1400表示转角处水平短筋从壁板内侧伸出的长度，X0、Y0分别表示可取消竖向、水平向短筋的范围。探讨X0和Y0的取值便可确定出取消竖向和水平向短筋的位置。本文研究L/H≥2的情况，其中L表示壁板的长度，H表示壁板的高度。

2 X0和Y0的理论解

2.1 基本假定

1.所研究的水池为地上式矩形敞口水池；

2.假定水池处于满水工况，且只研究壁板转角处在受到内水压力下的弯矩分布情况，忽略内水压力作用下产生轴向力对壁板配筋的影响；

3.假定壁板竖向和水平向均采用长短筋搭配的配筋方式，且长短筋的直径相同；

4.假定壁板等厚；

5.假定壁板的支座形式为三边固定顶端自由；

6.求理论解时，假定壁板转角处荷载按45°传递到相应支座。

2.2 求解X0

壁板竖向弯矩最大值出现在壁板中间的底端，设为MX，max，图4中A点的弯矩设为MA=MX，max/2。在A点取单位板宽计算，由力学知识可得（设水的容重为γ）：

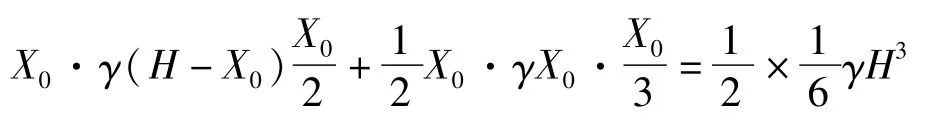
整理此式为标准一元三次方程：

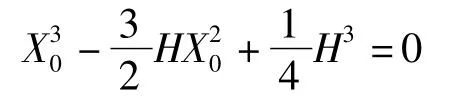
2.3 求解Y0

由文献［1］可知，壁板转角处水平弯矩最大值出现在壁板顶端，其值为MY，max=0.104γH3。设图4中B点的水平弯矩为MB=MY，max/2。在B点取单位板宽计算，由力学知识可得：

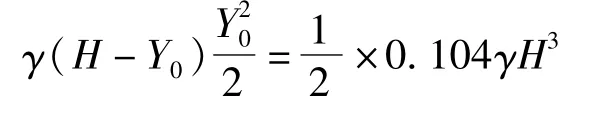
整理此式为标准一元三次方程：

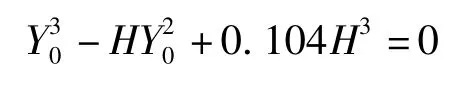
求得：Y0=0.425H，即

3 壁板转角处的有限元分析

3.1 相同壁板高度和长度，不同壁板厚度下的X0和Y0的分布规律

现假定壁板的长度L=15m，壁板高度H=5m，即L/H=3，壁板厚度h分别取0.3m、0.4m、0.5m、0.6m、0.7m，采用有限元软件分析壁板转角处在满水工况下的弯矩分布情况，找出最大竖向和水平向弯矩值的一半所对应的点，分别得出X0和Y0的值，见表1。

表1 相同壁板高度和长度，不同壁板厚度时的X0和Y0计算结果Tab.1 The results of X0and Y0at different thickness and same height and length of the wall

由表1可知，X0和Y0的值接近于恒定值。即当壁板高度和长度一定时，X0和Y0的值不随壁板厚度的变化而变化。

3.2 L/H一定时的X0/H和Y0/H的分布规律

现假定壁板的高度与壁板长度的比值一定，如取L/H=4，壁板长度L分别取12m、16m、20m、24m、28m，壁板高度H分别对应取3m、4m、5m、6m、7m，壁板厚度取0.1H。采用有限元软件分析壁板转角处在满水工况下的弯矩分布情况，找出最大竖向和水平向弯矩值的一半所对应的点。X0/H和Y0/H计算结果见表2。

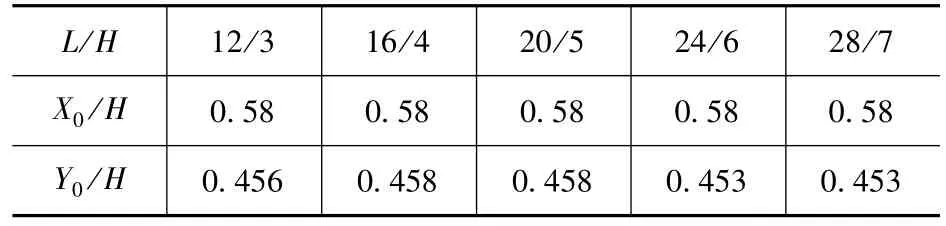
表2 L/H一定时的X0/H和Y0/H计算结果Tab.2 The results of X0/H and Y0/H at same L/H

由表2可知，X0/H和Y0/H的值也接近于恒定值。即当壁板高度与壁板长度的比值L/H一定时，X0/H和Y0/H的值与壁板具体尺寸没有关系。

3.3 X0和Y0的最终分析结果

不同L/H下，采用有限元软件分析壁板转角处在满水工况下的弯矩分布情况，可以得到X0/H和Y0/H的值如表3所示，X0/H和Y0/H与L/H的关系曲线分别见图5和图6。

表3 不同L/H下的X0/H和Y0/H计算结果Tab.3 The results of X0/H and Y0/H at different L/H

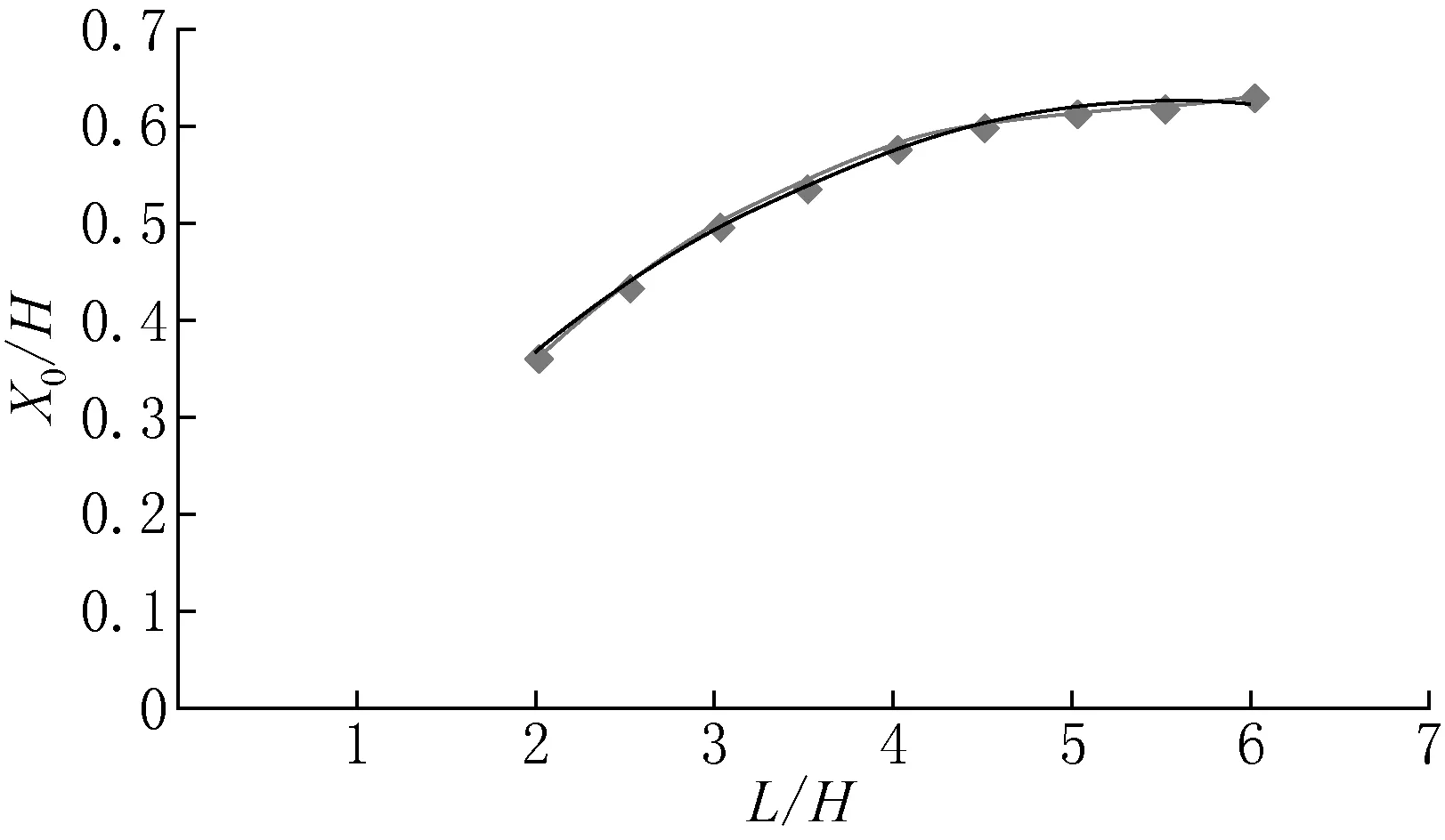
图5 X0/H与L/H的关系曲线Fig.5 The relation curve for X0/H and L/H

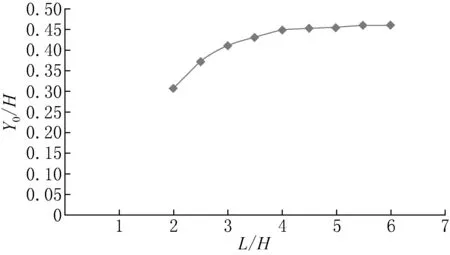
图6 Y0/H与L/H的关系曲线对比Fig.6 The relation curve for Y0/H and L/H

由表3、图5和图6可知，X0/H和Y0/H的值均随L/H的增大而增大。当L/H＞6时，考虑到工程实际情况，此类水池较少且为了简化考虑并结合关系曲线变化规律，可按L/H=6取值。

由X0/H和Y0/H的表达式与前面得到的理论解比较可得，理论解求得的X0和Y0均只与壁板的高度H成唯一的线性关系，而有限元分析得到的X0和Y0除了跟壁板的高度H有关，还与壁板的长度L有关。由表3得，仅当L/H=3时，X0/H有限元分析的结果与理论解相同；仅当L/H=3.3时（应用线性插值法），Y0/H有限元分析的结果与理论解接近。另外，当L/H的值增大时，X方向的刚度相对Y方向的刚度逐渐减小，根据刚度理论，转角处传递到X方向支座的荷载逐渐减小，对应图4中的角度由45°将逐渐减小，而理论解假定为45°保持不变。可见有限元分析的结果更加接近于工程实际情况。

因此，实际工程应用时，推荐采用有限元分析的结果，即可以直接采用表3来确定X0和Y0的值，当没有与表3相对应的L/H的值时，可采用线性插值法来求得X0和Y0。

4 经济效益分析

对于实际工程中的单块壁板，经大量数据统计发现，对壁板转角处采取精细化设计后可节省钢筋约8%～15%，对节省工程造价有着一定的现实意义。

举例说明，假设有一块壁板，壁板长度L=18m，壁板高度H=6m，壁板厚600mm，底板厚700mm。竖向和水平向按最大内力计算的配筋均为φ20@200（长筋）/φ20@200（短筋），其中单根竖向长筋总长度为6770mm，单根竖向短筋总长度为3350mm，由3.3节表3可得，X0=3000mm，可取消短筋的总长度为15×2×3350=100500mm；单根水平向长筋总长度为19020mm，单根水平向短筋总长度为3350mm，由3.3节表3可得，Y0=2480mm，可取消短筋的总长度为12.42×2×3350=83214mm。可节省钢筋的百分比为：（100500+83214）/（6770 × 90+3350 ×90+19020×30+3350×30）=11.6%。

5 结论

1.在壁板采用长短筋搭配的配筋方式时，在壁板转角处的一定范围内（X0和Y0）可以取消短筋，具体数值见表3。实际工程中，由于水平钢筋均在壁板转角处锚入相邻壁板，这会造成壁板转角处钢筋较密，施工中混凝土也往往难于振捣密实，在X0和Y0范围内取消短筋可降低施工难度，方便混凝土浇筑。

2.对壁板转角处采取精细化设计后可节省钢筋约8%～15%，值得推广。