南京长江大桥桥头堡大堡风振性能研究*

韩宜丹 淳庆，2

（1.东南大学建筑学院 南京210096；2.东南大学城市与建筑遗产保护教育部重点实验室 南京210096）

引言

在全球所有自然灾害中，风灾造成的损失为各种灾害之首。高层建筑结构的显著特点之一是侧向荷载在结构设计中起着决定性的作用，除了地震作用外，高层建筑结构主要的侧向荷载是风荷载，随着建筑高度的增加，以风荷载为主的水平荷载影响越来越大。

南京长江大桥建成于1968年，是长江上架起的第一座由我国自行设计和建造的双层式铁路、公路两用桥梁，其桥头堡大堡是一座高达70m的钢筋混凝土框架结构，2016年9月入选首批中国20世纪建筑遗产名录。南京长江大桥桥头堡大堡作为我国丰碑式的重要建筑物，风荷载对其影响更加不容忽视。南京长江大桥桥头堡大堡在设计当初，设计师曾对其进行过风荷载计算分析，计算结果于南京长江大桥工程简介［1］中有过介绍，但由于当时国内尚无成熟的相应计算规范，所以得出的结果必然与现行方法的计算结果存在一定差异。

目前学界鲜有针对中国建国初期桥头堡建筑的结构性能研究，仅有庄绍宁［2］通过ANSYS建立泉州火车站站前大桥桥头堡的有限元模型，计算得到该结构在时程风荷载下的位移及应力响应情况。章萍［3］分析了某桥头堡钢筋混凝土巨型塔柱框架结构体系，探讨了桥头堡结构的梁柱刚性节点设计、抗震性能措施和抗裂性能措施。Larose［4］以及Siringoringo［5］通过在桥头堡结构中安装振动传感器装置得到结构的速度、加速度及位移等响应结果，总结得到桥头堡的动力特性。本文将根据南京长江大桥桥头堡大堡的结构现状，分别建立不考虑填充墙影响情况和考虑填充墙影响情况下的大堡有限元模型，进行桥头堡大堡的风振性能研究，并与设计之初的计算结果进行比较分析，为南京长江大桥桥头堡的加固修缮提供科学依据。

1 南京长江大桥桥头堡大堡概况

南京长江大桥桥头堡是位于大桥正桥两端的桥头建筑，将正桥与引桥融合成一整体，雄伟壮丽，风格新颖。桥头建筑为复式桥台，两岸各有一座大、小堡。大堡塔楼高达70m，每座长17m，宽11m，占地面积175m2。除红旗层外，大堡共十层，七层以下每层高约6.9m，七层以上层高减少。四层与铁路面相通，七层与公路同一平面，对游人开放，八层为休息室，九层为水箱及电机房，十层为瞭望层，顶上为红旗平台。长江大桥的现状如图1所示。

图1 南京长江大桥桥头堡大堡现状Fig.1 Present situation of the major bridgehead

首先对桥头堡建筑的几何尺寸进行现场测绘复核，每座大堡塔楼共布置截面尺寸为50cm×50cm的立柱22根。其在七层及以下的平面布置见图2a。塔楼的楼梯布置，主层的楼版布置见图2b，夹层的楼版布置见图2c。纵向刚架第5～6排间，一半为电梯井道，一半为管道间，在管道间的每层均设有楼版。第8层及以上的平面布置见图2d。大堡除底层为24mm厚的实心墙外，其余均为20mm厚的空心砖墙。塔顶层红旗层为钢桁架结构，红旗旗面长边长9.3m，短边长6.6m，旗面为3mm厚钢板。

图2 大堡框架结构示意Fig.2 Frame structure of the major bridgehead

对大堡进行材料强度的现场无损检测，通过回弹法测得大堡的混凝土强度等级为C15～C25之间，本文对桥头堡大堡进行计算分析时，取混凝土强度等级为C15。

2 大堡设计之初的风荷载计算结果

根据南京长江大桥工程简介［1］中的计算方法，当时对于长江大桥桥头堡大堡的塔楼风力计算采用静力计算的方法，计算过程中施加于结构的平均风压为0.5kN/m2，并根据当时的荷载暂行规范，风荷载的计算考虑了以下五个系数的影响：重要建筑物系数1.2，超载系数1.3，振动系数1.5，空气动力系数以及高度影响的折减和增值系数（具体可参见1970年发布的《建筑工程部荷载暂行规范》）。其中，超载系数是指建筑物在各种未知的不利因素影响下的偶然极大荷载与相应的标准荷载间的比值，振动系数即指现行荷载规范中定义的风振系数，空气动力系数即指现行荷载规范中定义的风压体型系数，高度影响的折减和增值系数即指现行荷载规范中定义的风压高度变化系数。

计算过程中假定各层楼板是绝对刚性的，风力分配由顶层开始往下逐层分配，并假定计算层的下层楼层为固定端，即略去该层的转角对位移的影响。计算是利用“形变分配法”，首先求出各排刚架的代替悬臂的节点的劲率、主形变系数及次形变系数。其次，进行风力的分配计算，从红旗层刚架开始逐层往下计算，得横向各排刚架各层节点上的风力值。用“迭代法”（卡尼法）可解得各杆件的内力和结构的位移。通过该方法计算得到顶端位移最大值为7cm。

在计算位移时没有考虑四周填充墙对刚度的影响。并且该计算方法略去了各计算层下端的角变的影响，由于在计算时采用逐层往下分配，代替悬臂也同样逐层往下放松，因此对风力的分配值有一定的误差。另外该计算是在长江大桥施工前完成的，大桥在具体施工时曾做了一定程度的改动，如计算时红旗层是按照混凝土框架结构考虑的，而施工时支承红旗的顶部二层刚架已改用钢结构，并且在公路面上增加了一层楼层，后期的改动会给风力计算结果带来一定的影响，但风力计算没有重算。

本文根据长江大桥大堡建成后的结构现状建立有限元模型，模型中考虑红旗层为钢桁架结构，并考虑有无填充墙对大桥刚度的影响两种情况，利用脉动风压时程分析的方法进行风振性能研究，并与设计当初的风荷载计算结果进行比较分析。

3 无填充墙的大堡结构模型

3.1 无填充墙结构有限元模型建立

本文采用有限元软件SAP2000建立南京长江大桥大堡在不考虑填充墙影响时的有限元模型。大堡主体为混凝土框架结构，其上部的红旗骨架为钢结构，旗面为钢板。有限元模型中梁、柱及红旗骨架用框架单元模拟，楼板及红旗旗面用壳单元模拟。梁柱节点、柱与基础节点均采用固接节点。图3为大堡的有限元计算模型，模型中坐标系说明如下：X向为垂直于旗面的方向，Y向为顺旗面方向，Z向为竖直方向。

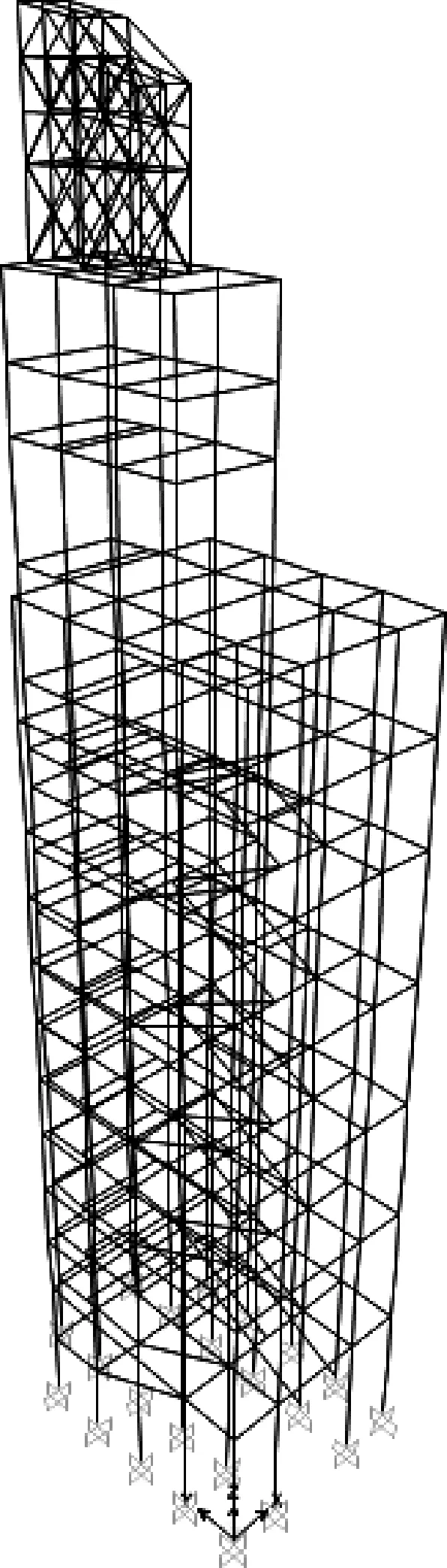
图3 桥头堡大堡有限元模型Fig.3 Finite element model of the major bridgehead

3.2 模态分析

振动模态是弹性结构固有的、整体的特性。通过模态分析的方法可以了解这一结构物在某易受影响的频率范围内的各阶主要模态的特性，就可以对结构在此频段内在外部或内部各种振源作用下产生的实际振动响应进行初步判断。本文利用有限元软件SAP2000计算出大堡结构的前12阶振型，结构自振周期、自振频率及振型参与质量系数见表1。

表1 大堡结构的自振周期、自振频率及振型质量参与系数Tab.1 Natural vibration period，frequency and model participating mass ratios of the major bridgehead

由表1可知，大堡结构基频为f=0.509Hz。结构的振型通过振型参与质量系数可以得到：一阶振型UX+UY＞RZ且UX＞UY，即一阶振型为X向水平振动；二阶振型UX+UY＜RZ，即二阶振型为绕Z轴的扭转振动；三阶振型UX+UY＞RZ且UY＞UX，即三阶振型为Y向水平振动，结构前三阶振型如图4所示。四阶振型为弯曲振动，四阶之后是比较复杂的平、扭耦合振动。结构X向平动自振频率明显小于结构Y向平动自振频率，说明结构刚度方向分布的差异，X向刚度明显小于Y向刚度。

为了控制结构扭转效应的潜在破坏力，《高层建筑混凝土结构技术规程》（JGJ 3-2010）［6］中规定，对于B级高度的建筑、混合结构高层建筑及复杂高层建筑，结构扭转为主的第一周期与平动为主的第一周期之比不应大于0.85。根据计算结果，大堡结构扭转第一周期和平动第一周期之比为0.83，满足现行规范要求。

图4 大堡结构前三阶振型Fig.4 Top three modes of the major bridgehead

4 不考虑填充墙影响时的结构风振分析

4.1 风荷载生成

建筑结构风荷载的计算方法有《建筑结构荷载规范》（GB 50009-2012）［7］（以下简称荷载规范）提供的静力分析方法和脉动风压时程分析方法。其中，静力分析方法即把风荷载当做静力荷载，风的动力效应则通过风振系数来体现。脉动风压时程分析法则更加精确，将风荷载考虑成动力荷载，即不计风振系数，直接利用风荷载时程考虑对于结构的脉动作用。我国荷载规范规定，对于高度大于30m且高宽比大于1.5的房屋和基本自振周期大于0.25s的各种高层结构以及大跨度屋盖结构，均应考虑风压脉动效应对结构产生的风振影响。因此，大堡需要考虑风压脉动效应对结构产生的影响。

本文根据文献［8］，采用线性滤波法中的自回归法（Auto-Regressive，AR）模拟风速时程，生成作用于大堡结构的风场。风速谱采用我国规范计算采用的Davenport谱，根据文献［9］，时间步长的最优取值范围为0.1s～0.18s，故本文选取时间步长为0.1s。根据上述理论，利用MATLAB编制应用于大堡结构的风速时程曲线，相关参数按表2取值。

据此生成脉动风速时程曲线及模拟功率谱与目标功率谱对比如图5所示。从图中可以看出在整个模拟频域范围内，模拟功率谱与目标功率谱基本吻合。

表2 风速时程模拟时的主要参数Tab.2 Parameters of simulated fluctuating wind speed

图5 脉动风速时程曲线及功率谱对比Fig.5 Time history curve of fluctuating wind speed and comparison of power specrum

风压时程和风速时程存在以下关系：

式中：W（t）为风压时程，kN/m2；v0为标准风压下的风速，m/s；v（t）为程序生成的脉动风速时程。依此生成风压时程曲线见图6。

图6 风压时程曲线Fig.6 Time history curve of fluctuating wind pressure

4.2 大堡风压体型系数

作用于大堡结构上的脉动风荷载时程函数为：

式中：F为结构受到的风荷载时程；A为施加风荷载的面积；W为风压时程；μs为风荷载体形系数。

对大堡结构开展风振响应分析时，考虑风荷载沿X向，由模态分析可知大堡沿X方向刚度薄弱。根据荷载规范中的表8.3.1，并参考文献［1］得到大堡的风压体型系数，见表3。将上述荷载施加于结构，大堡的填充墙设置为虚面，风荷载通过虚面导荷至框架结构，求解出大堡结构的风振响应结果。

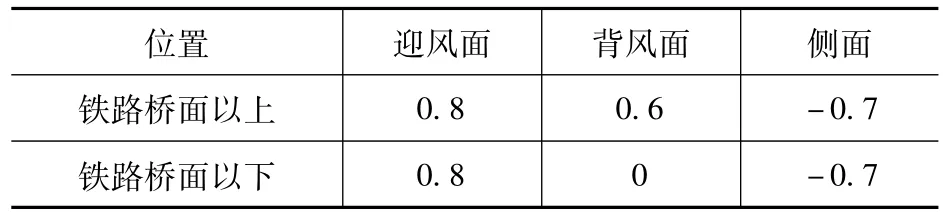
表3 大堡风压体型系数Tab.3 Wind pressure coefficients of the major bridgehead

4.3 大堡位移响应分析

当对大堡进行风荷载时程分析时，结构阻尼比取值0.035。为得到时程风压对大堡结构的脉动效应，将脉动时程风压下的结构位移与静风荷载下结构的位移进行对比分析。首先，根据现行的《建筑结构荷载规范》［7］对大堡结构有限元模型施加静风荷载，风荷载标准值取0.5kN/m2，同时考虑结构重要性系数1.1，以及风压高度变化系数，得到大堡结构在静风荷载下的位移响应。将上述计算生成的时程风压施加于大堡结构有限元模型，得到大堡在时程风荷载下的响应结果。并将静力风压下的结构位移最值（u0）与时程风压下的结构位移最值（umax）进行比较，可以得到结构的风振系数（β=umax/u0），并得到大堡楼层的层间最大位移Δmax，各位移响应结果见表4。

表4 大堡静风及时程风压下位移值对比Tab.4 Comparison of displacements under static wind and time history wind

根据设计当初的静力计算方法得到的大堡结构顶端位移计算最大值为7cm，而本文中按照现行规范中静力计算方法得到的结构位移最大值为6.14cm，时程风压下结构顶端的位移最大值为11.59cm。本文得到的位移结果与设计之初得到的位移结果存在一定差异，这是由于本文中大堡的有限元模型是按照大堡建成后的实际结构建立的，并且红旗层为钢结构，而设计之初计算红旗层是按照混凝土框架结构考虑的。此外，本文研究中所施加的静风荷载是根据现行规范得到，而设计之初计算时施加的荷载是按照当时的暂行规范取值，其中荷载的各个放大系数与现行荷载规范的计算方法均不同。本文研究中施加时程风荷载能够更精确地反应风对结构的脉动效应，大堡设计之初计算方法中的考虑振动系数即风振系数取值为1.5，由表4可以看出本文得到大堡结构的风振系数取值在1.81～1.96之间。

根据《高层建筑混凝土结构技术规程》［6］，对于高度不大于150m的高层框架结构建筑，其楼层层间最大位移与层高之比不宜大于1/550。由表3可知，除一层、九层、十层外，楼层的层间最大位移均超过允许值。

5 有无填充墙影响时的大堡响应对比分析

上述计算过程未考虑填充墙对结构风振性能的影响，仅将砌体填充墙作为竖向恒荷载施加在结构上。在我国《建筑抗震设计规范》［10］中规定填充墙为非结构构件，填充墙主要起隔墙和围护的作用，填充墙不参与结构的抗震计算。但在风荷载作用下，填充墙的存在可提高结构的抗侧刚度，从而使结构的自振周期减小。所以，带填充墙的框架结构在进行风振性能计算分析时需充分考虑填充墙对框架结构的影响，并不能简单地将带填充墙的框架结构的自振周期乘以一定折减系数。因此本文将在有限元模型中考虑填充墙对结构的作用，并与上述计算结果进行对比分析。

5.1 填充墙模拟方法

目前，带填充墙框架结构的计算分析模型主要有两种：一种是通过将结构划分成大量的单元来分析结构细部性能的微观有限元模型，但由于模型中较多参数的不确定性和较高的计算代价，微观有限元模型难以得到应用；另一种是宏观模型，宏观模型是基于在水平荷载作用下填充墙表现出对角受压杆的受力机制而提出的，即利用斜支撑模拟填充墙对框架的作用。等效斜撑模型是将填充墙模拟为与梁柱交点铰接的，受压不受拉力的，与框架共同工作的抗侧力构件。该等效斜撑如图7a所示，其与墙体材性相同，截面为矩形，长度为梁柱间对角线长度，厚度同填充墙厚度，等效斜撑具有一定宽度，其宽度由式（4）和式（5）确定。本文采用Buonopane［11］提出的开洞填充墙的斜支撑模型来模拟大桥大堡的填充墙，如图7b所示，单根斜压杆宽度按照尺寸由洞口两侧墙肢尺寸的非开洞填充墙确定［12-14］。

其中：λ为刚度系数；Ew为填充墙的弹性模量；tw为填充墙的厚度；θ为填充墙对角线与框架梁之间的夹角；Ec为框架柱的弹性模量；Ic为框架柱的惯性矩；Hw为填充墙体的髙度；Dc为等效斜撑宽度；H为框架柱高度；L为框架梁长度。本文计算模型中，一层填充墙Ew0取值为2704MPa，其余层Ew取值为1984MPa；墙厚一层tw0取值为240mm，其余层tw取值为200mm；Ec取值为2.6×104MPa。斜撑的材料属性与填充墙的材料属性一致。依据上述理论建立长江大桥大堡的有开洞填充墙混凝土框架结构的有限元模型。

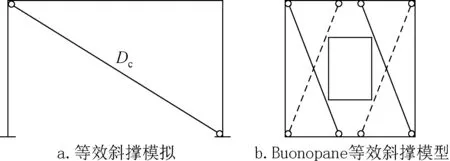
图7 等效斜撑模拟及Buonopane模型Fig.7 Equivalent inclined bracing simulation and Buonopane model

5.2 考虑填充墙影响后的模态分析

考虑填充墙影响后，结构的刚度、周期、承载力、层间位移、塑性发展和结构构件内力都会发生较大的变化，考虑填充墙影响后的有限元模型能够更加准确地反应大堡的结构特性。表5为考虑填充墙影响的结构周期及振型质量参与系数，可以看出与未考虑填充墙作用的结构模型相比，结构的自振周期、自振频率和振型发生明显变化，自振周期减小，结构刚度增大，一阶振型为X向水平振动，二阶振型为Y向水平振动，三阶振型为绕Z轴的扭转振动。由于通过斜支撑模拟填充墙使结构的整体扭转效应大大减小，结构扭转第一周期和平动第一周期之比为0.62，满足荷载规范要求。

表5 考虑填充墙影响的结构周期及振型质量参与系数Tab.5 Natural vibration period and model participating mass ratios of the major bridgehead considering infilled walls

5.3 加速度响应分析

将同样的时程风荷载作用于考虑填充墙影响的结构模型，得到时程风振响应结果。结构的位移及最大层间位移等结果见表6。其中，u′0为静风荷载下考虑填充墙影响的结构位移最大值，u′max为时程风压下的考虑填充墙影响的结构位移最大值，Δ′max为考虑填充墙影响的结构最大层间位移。结构的位移及最大层间位移均明显减少，其楼层层间最大位移与层高之比均在允许值之内。考虑填充墙影响的结构最大层间位移折减为不考虑填充墙影响的结构最大层间位移的46%～74%，结构的风振系数取值在1.79～2.10之间。

对风荷载作用下考虑填充墙影响和不考虑填充墙影响下的结构红旗层最大位移与设计当初的计算结果进行比较分析，结果如表7所示。结果表明：在有无填充墙影响的情况下，按照荷载规范中静载法计算得到的最大位移均小于设计当初的计算结果；按照时程法计算得到的最大位移均大于设计之初的计算结果。由此可以看出，本文的风振响应结果与大堡设计之初计算结果存在一定差异，风对大堡产生的脉动效果以及填充墙对于结构抗侧刚度的贡献均不可忽略。总体而言，在考虑填充墙影响时采用荷载规范中风荷载时程法的计算结果更加接近于大堡设计之初的风荷载计算结果。另外，九、十层层高明显低于一到八层层高，对于考虑填充墙与不考虑填充墙影响的最大层间位移之比Δ′max/Δmax，第九、十层的数值明显比其它层大，填充墙（斜撑）对九、十层抗侧刚度的影响比对其他层的影响小。

表6 大堡静风及时程风压下位移值对比Tab.6 Comparison of displacements under static wind and time history wind

表7 风荷载作用下的红旗层最大位移计算比较Tab.7 Comparison of the maximum displacements of flag floor under wind pressure

5.4 加速度响应分析

此外，本文也对风荷载作用下的结构加速度响应进行了分析，表8中列出了在时程风荷载作用下，有无填充墙影响的结构各层加速度峰值。结果表明：考虑填充墙影响后结构各层的加速度峰值显著减小。另外，风荷载作用下结构的振动还应满足人体的舒适度要求。大堡的一层及七层平台对游人开放，对于大堡而言，无论是供游人观景还是供工作人员办公，风荷载作用下引起的结构振动或造成建筑内人员的不适都应予以避免。结构的振动持续时间、振动频率以及结构振动的加速度是影响人体感觉舒适度的主要因素。其中，结构振动的持续时间取决于风荷载作用持续时间，对于既有建筑而言，调整结构的频率是很难实现的，因此一般采用限制结构振动加速度的方法来满足人体舒适度的要求，结构加速度的控制界限可以通过人体振动舒适界限标准得到，当结构加速度达到0.15m/s2就会使人烦恼，当结构加速度达到0.5m/s2就会达到让人非常烦恼的程度，结构加速度达到1.5m/s2会让人无法忍受［15］。由表8可以看出，即使考虑填充墙影响后，除一层外，各层的加速度峰值都达到了使人烦恼甚至让人非常烦恼的程度。故应采取适当措施对风振作用下的加速度峰值进行控制，尽量使之符合人体舒适度要求。

6 结论

1.大堡在不考虑填充墙影响时，结构基频为f=0.509Hz；一阶振型为X向水平振动，二阶振型为绕Z轴的扭转振动，三阶振型为Y向的水平振动。结构扭转第一周期和平动第一周期之比为0.83，满足现行规范要求。

2.在不考虑填充墙影响时，静力计算得到结构位移最值为6.14cm，时程风压下结构顶端的位移最值为11.59cm，时程风压计算得到的风振系数取值在1.81～1.96之间。大堡除一层、九层、十层外，楼层层间最大位移与层高之比均超过允许值1/550。

3.在考虑填充墙影响时，结构的自振周期和振型发生明显变化，结构基频为f=0.580Hz，自振周期减小，结构刚度增大；一阶振型为X向水平振动，二阶振型为Y向水平振动，三阶振型为绕Z轴的扭转振动。结构扭转第一周期和平动第一周期之比为0.62，满足现行规范要求。

4.考虑填充墙影响时，结构在时程风压下的位移及最大层间位移等结果均显著减少，其楼层层间最大位移与层高之比均在允许值1/550之内。考虑填充墙影响时的结构最大层间位移折减为不考虑填充墙的46%～74%。填充墙对于结构抗侧刚度的贡献不可忽略。时程风压计算得到的风振系数取值在1.79～2.10之间。

5.考虑填充墙影响时，除一层外各层的加速度峰值都达到了使人烦恼甚至让人非常烦恼的程度。故应采取适当措施对风振作用下的加速度峰值进行控制，尽量使之符合人体舒适度要求。