无线网络信号模型的自回归参数估计
□韩 睿,来晓东
( 1.山西职业技术学院,山西 太原 030009;2.山西广播电视大学,山西 太原 030027)
1.瞬时频率
自回归建模方法已广泛用于语音处理和高分辨率的信号谱估计领域中。基于的AR模型技术已被证明[1]可以用于区域级/ NAMPS信号的解调,我们的工作就是将该项技术扩展到正被广泛应用在多种无线通讯系统中的GMSK信号上。分布参数或分布律具有时间依赖性的信号被称为非平稳信号。瞬时频率在非平稳信号分析中是一个非常重要的物理量,在许多信号处理的实际应用领域中瞬时频率估计占有着非常重要的地位。所有静止的信号都可以表示为特定频率的正弦和余弦的总和。 然而,对于非平稳信号,例如Chirp信号,这是不成立的,因为信号扫描频率超过了波段频率的观察时间间隔。 通常处理这一问题的办法是使观察间隔尽可能小,信号可以被假定为一个正弦波(假设为单组分信号)。如果数据记录的可用IF估计将非常小,那么就引出了我们将在下面要讨论的频率分辨率的问题。信号可以用以下形式表示:
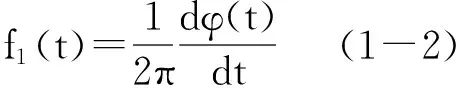
即瞬时频率是相位对时间的导数[2]。需要注意的是,如果频率fi(t)为常数时,公式(1-1)可简化为:
s(t)=acos[2πft+θ] (1-3)
通常中频通信信号是由一个频率固定的分量(即载波)和一个随时间变化的分量构成的,该分量中包含了所要传送的信息。如果振幅a或相位θ的调制方式分别为随时间变化的振幅调制和相位调制时,信号可表示为:
瞬时频率的公式为: f1(t)=fe+fm(t) (1-5)
其中,fc是频率恒定的载波部分和fm是信息承载部分。
2.频谱估计技术
自回归移动平均模型(ARMA模型)是最常用的有理转移函数模型,并可以由下面的差分方程表示:
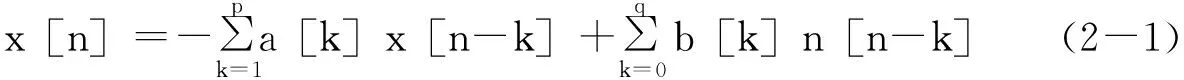
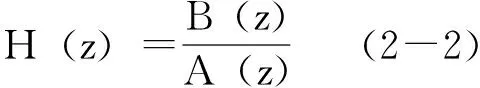
该输出序列的功率谱密度(PSD)是:
需要注意的是,u[n]是一个在模型中包含的固定部分,不应与观测噪声混淆。ARMA模型也被称为零极点模型。如果我们使MA模型中除a[0]外的所有分母系数都等于零。我们的MA模型的差分方程(2-1)将简化为:
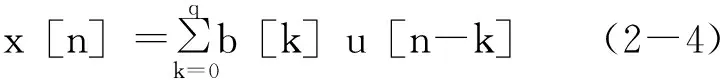
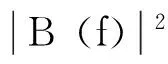
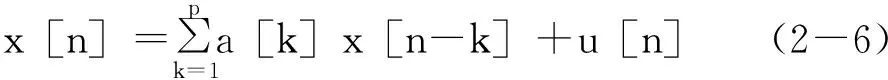
我们假定了a[0]=b[0]=1。如果数据是由纯正弦波构成的,那么AR模型通常是最好的选择。这是因为极点AR模型能准确表示频率域中的离散信息。
3.模式选择
信号谱估计模型的选择过程有三个步骤,如图1-1所示。第一步是选择一个具有先验信息数据资料的基本模型。 我们知道,信号是一个非稳定的调频信号,即信号的频率是随时间变化的,但在小型观测窗口中,信号可以被认为是稳定的。所以信号基本上会包含一个较完整的噪声正弦曲线。

图1-1基于模型的谱估计步骤
即在同信道干扰中将存在有一个以上的正弦分量。因此,选择的应该是能够准确代表正弦分量并同时具备一个较高的频率分辨率的模型。 由上述规定的要求可以很明显得出结论,AR模型将是最适当的选择。经典技术无法为客户提供高频率分辨率和窄带程序模型[5]。在模型的选择中,MA模型或ARMA的优先级顺序比AR模型要低。AR模型已被广泛应用在许多信号处理的领域。它已被证明AR模型可以用来精确地表示AMPS / NAMPS信号,并能够提供比传统正交解调器的更好的性能增益。另一个选择AR模型的原因是,我们可以利用它来进行更有效率的计算,这种方法与传统的非相干解调技术有紧密的相似性。然后,我们选择数据模型的下一个步骤就是确定模型参数,一个模型的最佳阶数为L=3N/4,这也就是我们在模拟中最常用的参数。在确定模型参数之后,即可将这些参数代入模型以获取AR谱估计。由(2-6)和(2-7)给出的AR模型,可以用图 1-2中显示的IIR滤波器来表示。在这里,模型可以由驱动噪声序列u [n]和参数a1,a2,……ap来完全定义。
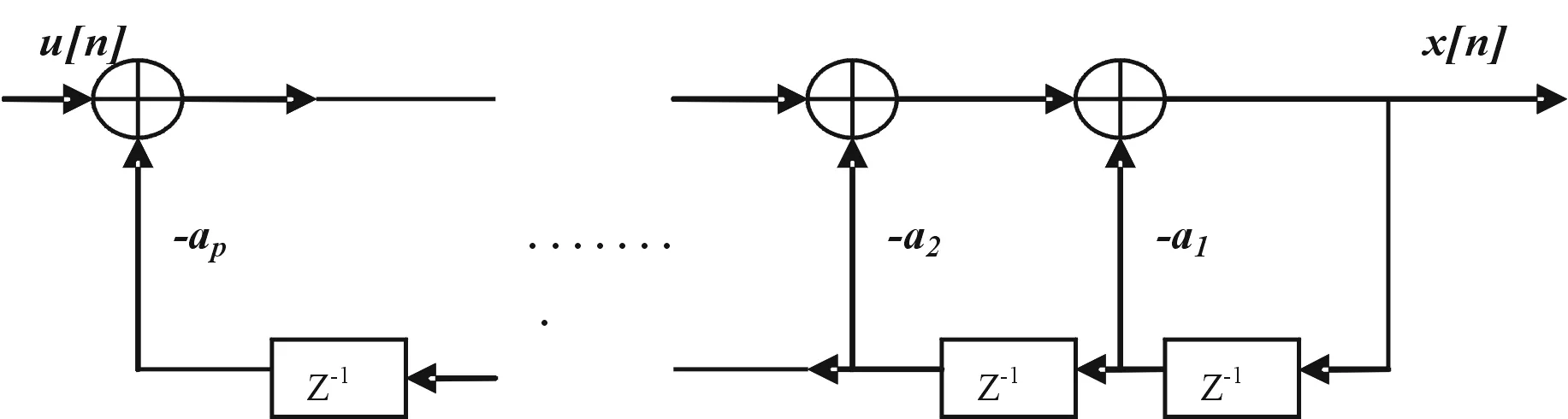
图1-2 AR模型信号流程图
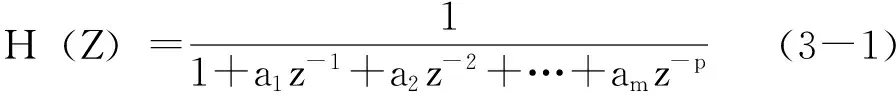
在确定AR模型的线性预测系数参数时,线性预测方程可写为
其中,{a1,a2,……ap}是预测系数,而预测误差则为:
滤波器的输出可以表示为:
z[n]=ejφ[n+1]ejφ[n]=ejφ[n+1]-φ[n](3-4)
对于一个一阶滤波器的线性预测方程可表示为:
x[n-1]a[1=-x[n] (3-5)
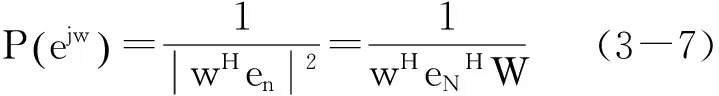
这就是所谓的伪谱,因为它只提供了有关信息的位置复指数,而不是他们的权。该方法可以消去音频信号的最主要的相关性限制矩阵。伪谱可定义为:
其中噪声E是指噪声特征向量矩阵:
Enoise= [eM+1eM+2… eN] (3-9)
假设复杂的指数函数M的数量是已知的。因此,特征向量数目是大于复指数的数量。该特征值对应的最小特征值和噪音是由特征向量定义的,它是正交的信号载体。
ESPRIT是一个比较新的子空间技术,提供了大幅提高频率分辨率的解决方案。原来的ESPRIT算法,提出了在该方案框架下的相关数据矩阵,但存在有严重的数值问题。最小二乘法(LS)和总体最小二乘法(TLS)是用来解决这些问题首选方法。 ESPRIT算法的子空间方法与其他方法不同,它进行频率估计时使用的是离散信号子空间,而不是噪音子空间。这种方法的关键是要分成两个信号交错子的空间。让我们定义一个信号矩阵S为:
然后两个矩阵 S1、S2是分别消除第一行和最后一行的剩余部分。
这两个矩阵是相关的: S2=S1Φ (3-10)那么
显然,矩阵 包含的频率信息。如果S1和S2为已知,则 很容易使用最小二乘法。
4.模拟结果
在测试中,我们使用LTE-YD-02B1移动通信系统综合实验箱系统中的基带成形模块,产生PN31伪随机序列作为信源;将基带信号进行串并转换;按QPSK、OQPSK、MSK、GMSK调制要求进行基带成形,形成测试信号。并采用 Matlab 编程,生成最终的测试结果。
在比较时选择的信号是高斯滤波的带宽为3dB ,BT= 0.5 的MSK(GMSK调制)信号。我们使用复杂基带模型进行了模拟,采样频率fs=20。对于在AWGN信道下的基于模型的解调器的执行情况使用主成分分析法(PCM)的结果如图2-1 - 2-3所示(规定信噪比为30dB)。
当存在同信道干扰的情况下,基于模型的设计(MBD)的性能如图2-1所示。同时,限幅鉴别频器(LD)的表现也显示出来以供参考。可以看出,在具有独立的过滤器的长度L或数据样本数N的情况下,MBD和LD具有相同的误码率性能。但是,MBD与LD在不同的相位差下的表现则不具备相关性。接下来,我们对MBD测试实例进行评估。我们采用LMS算法来跟踪滤波器的系数,而不是为每一个系数进行单独的计算。我们将步长设置为0.005,结果发现迭代次数为10时,LMS算法足以减少预测误差。而再进一步的迭代则无法继续提高误码率性能。从结果中可以看出,如果滤波器的阶数大于3,在性能上就会有明显的降低。
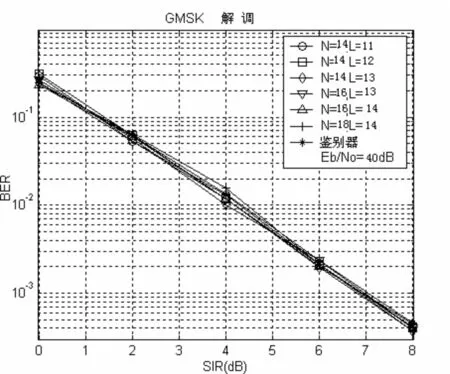
图2-1 LD和基于模型的解调器在各种滤波器长度下的性能表现
如果有一个单列的正弦分量信号,那么第一个角度的系数就可以用于频率估计。事实上,如果信号具有足够的过采样,且所有过滤系数都具有相似的值和正弦分量,那么我们就可以通过角度来确定任何一个相关系数。所有上述测试方案的性能比较如图2-2所示。最后我们在瑞利衰落环境中对MBD的性能进行评估。可以看出,MBD与LD的表现相似,衰落是缓慢的并且是与频率不相关的。我们设置了两个极端的情况:一是两种信号经历了完全不相关的衰落。二是两种信号经历了相同的衰落。可以看出,在不相关衰落的情况下,其性能更差。在第二种信号经历了相同的衰落情况下,性能主要由两个信号的相对强度来决定。在实际运行环境中,两个信号所经历的衰落与性能表现将会介于两个极端情况之间。
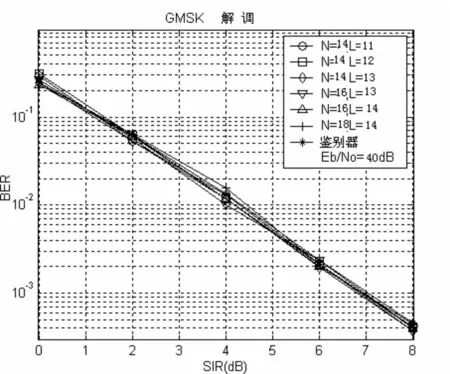
图2-2 以各种模型为基础的解调方案的性能比较
5.结语
我们在自回归模型的基础上,针对中频信号的特性提出了高频率分辨率的要求。然后讨论了AR模型参数的确定问题,我们采用了最小二乘法来确定AR参数,这种方法的优点在于它是直接应用于数据而无需对自相关函数求解。同时,我们选用LMS算法来跟踪滤波器的系数,以免于对每一个系数进行单独的计算。而AR模型的谱估计可以通过将参数代入到模型中来获得。模拟结果显示,基于模型的设计(MBD)与常规的限幅器/鉴频器在各类环境中进行比较后,总体上并无十分明显的优势,只有当载波频率之差为1/2T时,MBD才会提供较好的性能提升。
:
[1]Boualem Boashash, Estimating and Interpreting the Instantaneous Frequencyof a Signal - Part 1: Fundamentals[J].Proceedings of the IEEE , 1992, 80(4) :2136-2138.
[2]Boualem Boashash, Estimating and Interpreting the Instantaneous Frequency of a Signal - Part 2: Algorithms and Applications[J].Proceedings of the IEEE, 1992, 80(4):566-569.
[3]S. Lawrence Marple Jr. Spectrum Analysis: A ModernPerspective[J].Proceedings of the IEEE, 1981,69(3):1380-1419.
[4]S. Verdu.Multiuser Detection[M].Cambridge University Press, Cambridge,1998:53-66.
[5]Mathew L. Welborn.Co-Channel Interference Rejection Using a Model-Based Demodulator[D].Virginia Polytechnic Institute, 1995.

