具有常数输入的SEIR和SEIS组合传染病模型的分析

孙志强

(河南艺术职业学院基础教学部，河南郑州 450011)

具有常数输入的SEIR和SEIS组合传染病模型的分析

孙志强

(河南艺术职业学院基础教学部，河南郑州 450011)

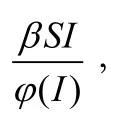
传染病模型；传染率；平衡点；稳定性

1 建立模型

2 平衡点的存在性和稳定性

[1] Hethcote H W. The Mathematics of infectious diseases [J]. SIAM Review, 2000, 42(4): 599-653.

[2] Li J, Ma Z. Qualitative analysis of SIS epidemic model with vaccination and varying total Population size [J]. Mathematical and computer Modelling, 2002, 20(5): 1235-1243.

[3] Capasso V, Serrio G. A generalization of the Kermack-Mckendrick deterministic epidemic Model [J]. MathematicalBiosicences, 1978, 42(2): 327-346.

[4] 王拉娣. 一类带有非线性传染率的SIRS传染病模型[J]. 华北工学院学报, 2005, 26(1): 1-5.

[5] 宋贽, 惠淑荣, 陶桂洪, 等. 具有非线性传染率的一类传染病模型的定性分析[J]. 沈阳农业大学学报, 2008, 39(3): 377-380.

[6] 王拉娣. 具有非线性传染率的两类传染病模型的全局分析[J]. 工程数学学报, 2005, 22(4): 640-644.

[7] 韩丽涛, 原三领, 马知恩. 两种群相互竞争的SIRS传染病模型的稳定性[J]. 生物数学学报, 2003, 18(1): 21-26.

[8] 王拉娣. 一类含有非线性传染率的传染病模型的全局稳定性[J]. 应用数学与计算数学学报, 2004, (1): 52-56.

Analysis of SEIR and SEIS Combination Epidemic Model with Constant Recruitment

SUN Zhiqiang
(Department of Basic Teaching, Henan Art Professional College, Zhengzhou, China 450011)

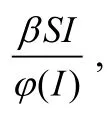
Epidemic Model; Incidence Rate; Equilibrium Point; Stability

O175.13

A

1674-3563(2012)05-0023-05

10.3875/j.issn.1674-3563.2012.05.004 本文的PDF文件可以从xuebao.wzu.edu.cn获得

(编辑：王一芳)

2011-11-07

孙志强(1979- )，男，河南郑州人，中教初级，硕士，研究方向：生物数学