捕食者有病的生态-流行病随机模型及分析
李广玉,王 克
(1.温州大学瓯江学院,浙江温州 325035;2.哈尔滨工业大学数学系(威海),山东威海 264209)
捕食者有病的生态-流行病随机模型及分析
李广玉1,王 克2
(1.温州大学瓯江学院,浙江温州 325035;2.哈尔滨工业大学数学系(威海),山东威海 264209)
建立并分析了捕食者具有流行病的捕食-被捕食模型的随机形式,并对平衡点进行了分析,得到了平衡点随机稳定的充分条件.
生态-流行病模型;平衡点;随机稳定
由于流行病必然在物种之间传播,所以将动力学和流行病动力学结合起来考虑更符合实际情况.文献[1]考虑了食饵有密度制约、疾病只是在捕食者之间传播且染病的捕食者会因病死亡的生态-流行病模型,假设染病的捕食者不捕食饵,模型为:


近年来,各种种群模型稳定点问题已成为生物数学的一个研究热点[2-3],与种群模型相关的随机稳定性也被广泛关注[4-9],例如文献[9]的模型为随机半比例型捕食与被捕食系统,通过构造V函数,证明了此随机方程正解的局部存在性及唯一性,进而证明了正解不会在有限时间内爆破.对于模型(1),已有很多学者进行研究,并得到了较好的结果.实际上,生物种群系统经常会受到环境白噪声的干扰,受文献[1]的启发,本文建立了捕食者具有流行病的捕食-被捕食模型的随机形式,并对奇点进行了分析,得到了平衡点随机稳定的充分条件.目前并没有相关的结果.
1 有关引理
首先给出一个有用的引理.
引理1 对于随机微分方程:
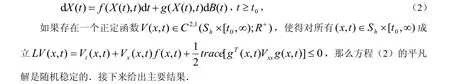
2 主要结果
首先对系统(1)进行整理得:




[1] 孙树林, 原存德. 捕食者具有流行病的捕食-被捕食模型分析[J]. 生物数学学报, 2006, 21(1): 97-104.
[2] 张江山, 孙树林. 捕食者有病的生态-流行病模型的分析[J]. 生物数学学报, 2005, 20(2): 157-164.
[3] 张亚光, 懂雨滋. 一类捕食者-食饵模型的稳定性分析[J]. 山西师范大学学报: 自然科学版, 2007, 28(2): 52-59.
[4] 陈晓鹰. 一类具有非单调增长率和功能反应的捕食者-食饵系统的定性分析[J]. 生物数学学报, 2005, 20(1): 122-127.
[5] 王战平, 张保文. 一类随机非线行种群发展系统的指数稳定性[J]. 固原师专学报: 自然科学版, 2006, (11): 68-73.
[6] 李荣华, 戴永红, 孟红兵. 与年龄相关的随机时滞种群方程的指数稳定性[J]. 数学年刊: A辑, 2006, 27(1): 39-52.
[7] 补爱军, 陈内萍, 孟红兵. 自然资源利用的随机模型及其动态分析[J]. 湖南师范大学自然科学学报, 2007, 30(1): 35-38.
[8] 陈森发, 张文红, 张建坤, 等. 短期降雨预测的随机微分模型[J]. 系统工程学报, 2004, 19(3): 96-103.
[9] 韩七星, 李秋月, 罗英语. 随机半比例型捕食与被捕食系统正解的存在性及唯一性[J]. 通化师范学院学报, 2006, 21(1): 97-104.
Eco-epidemiological Stochastic Model of Predator with Epidemic and Its Analysis
LI Guangyu1, WANG Ke2
(1. Oujiang College, Wenzhou University, Wenzhou, China 325035; 2. Department of Mathematics, Harbin Institute of Technology at Weihai, Weihai, China 264209)
In this paper, stochastic form of predator-prey stochastic model of predator with epidemic was established and analyzed. Then, the equilibrium points were studied to achieve the sufficient condition of the stochastic stability.
Eco-epidemiological Stochastic Model; Equilibrium Point; Stochastic Stability
O175.13
A
1674-3563(2012)05-0018-05
10.3875/j.issn.1674-3563.2012.05.003 本文的PDF文件可以从xuebao.wzu.edu.cn获得
(编辑:王一芳)
2011-12-20
国家自然科学基金(10701020);温州大学瓯江学院基金(JSKY09004)
李广玉(1979- ),女,黑龙江齐齐哈尔人,讲师,硕士,研究方向:随机微分方程及其应用

