关于计算多重积分的拟蒙特卡罗方法
张 涛,周仲礼,安素珍,张 军
(成都理工大学数学地质四川省重点实验室,四川成都 610059)
关于计算多重积分的拟蒙特卡罗方法
张 涛,周仲礼,安素珍,张 军
(成都理工大学数学地质四川省重点实验室,四川成都 610059)
介绍了拟蒙特卡罗方法计算多重积分的基本原理,对Halton序列和Rand函数产生的序列的均匀性进行了比较,并给出了拟蒙特卡罗方法计算多重积分的步骤、实例、和Matlab语言编写的计算程序.实例充分体现了采用拟蒙特卡罗方法计算多重积分的有效性、精确性和优越性.
拟蒙特卡罗方法;Halton序列;多重积分
在数学和工程科学计算中,求解多重积分的近似值是一个至关重要的环节.通常人们所采用的方法有3种,即蒙特卡罗方法、拟蒙特卡罗方法和数论网格方法.然而,在实际应用中,数论网格法很难解决高维问题,如对20维这样的问题,就要有一百万多个点[1],计算量大体上随维数的幂次增加,几乎是不可能计算的.蒙特卡罗方法是采用单和来得到多重积分的近似值的[2],计算跟问题的维数无关,克服了“维数灾难”,但其误差却是概率性的,得到解的精度不高.本文研究了拟蒙特卡罗方法在计算多重积分中的应用,并给出Matlab程序的实现.实例表明,采用拟蒙特卡罗方法计算多重积分,既能克服维数的制约,又能得到确定性的误差估计和更高精度的解.
1 拟蒙特卡罗方法基本原理及其优越性
拟蒙特卡罗方法也称低差异序列法,是在蒙特卡罗方法基础上发展起来的一种模拟方法.拟蒙特卡罗方法与蒙特卡罗方法相似,但所用的理论基础却不同.拟蒙特卡罗方法是通过构造所谓的低差异序列,即用的是确定性的点,然后用Koksma-Hlawka不等式来确定误差阶的,而不是根据大数定律[3].

卡罗方法模拟解积分问题的误差界可以表示为[3-4]:
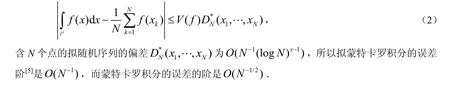
对于拟蒙特卡罗方法积分,我们有确定性的误差估计.在计算积分中还可以明智地选择这些确定的点来减小式(1)中的误差,得到高精度的解.因此,就确定性和高精度性这两点,拟蒙特卡罗积分要优于蒙特卡罗积分.对于更高维的积分问题,拟蒙特卡罗法优于数论网格法.
在过去的几十年里,拟蒙特卡罗法得到了快速发展,人们已经构造出大量优质的低差异序列,如Halton序列、Sobol'序列、Niderreiter的(t,m,s)网格和(t,s)序列等[6].本文主要研究Halton序列在计算多重积分中的应用.
2 Halton序列

下面将给出产生Halton序列的Matlab程序[7],并对Halton序列与Rand函数产生的随机数序列的均匀性进行比较,见图1.



图1 Halton序列与Rand函数产生的十维随机数点的均匀性比较
由图1可明显看出,Rand函数产生的伪随机数序列有抱团现象,分布不均匀,而Halton序列则要均匀得多.有了这样优质的均匀随机序列,用拟蒙特卡罗方法求解得到的将是确定性的误差,从而避免了蒙特卡罗方法得到概率误差的缺陷.
3 拟蒙特卡罗方法计算多重积分的均匀随机数平均值法


4 算例及其实现
下面给出两个特殊数值算例验证拟蒙特卡罗方法在计算多重积分中的有效性和优越性.
例1 用Halton序列计算s重积分

取N=2 000,在计算机上分别用Halton序列和Rand函数计算的结果见表1.
的估计值.

表1 分别用Halton序列和rand函数计算的积分结果


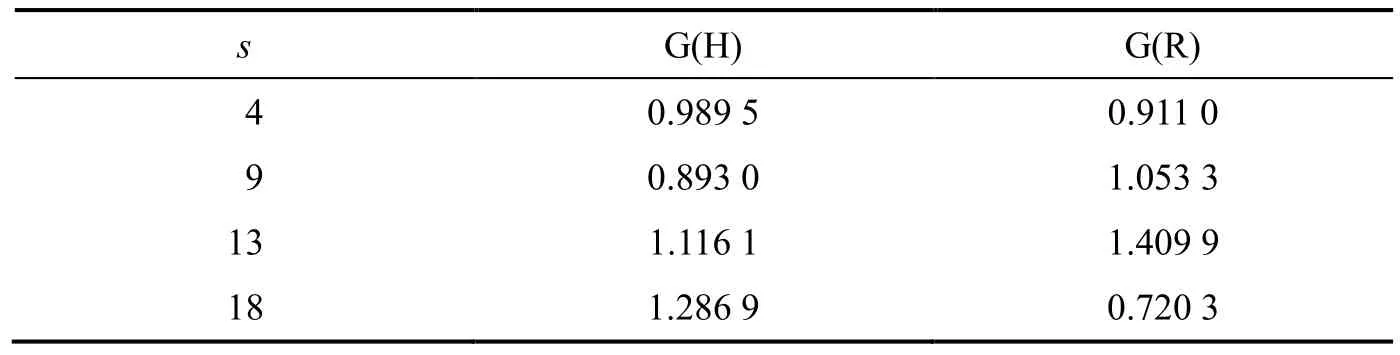
表2 分别用Halton序列和rand函数计算的结果

5 结 语
通过计算可以看出,拟蒙特卡罗方法是有效的,积分重数对积分结果的误差无明显影响,精度较高,计算机程序实现也是很简单的.本文只是用了原始的Halton序列,由于Halton序列基数越大,相关性也越大,均匀性也会越差,这将会影响结果的精度,因此,如何选择更优质的低差异序列有待进一步学习和研究.
[1] 雷桂圆. 关于蒙特卡罗及拟蒙特卡罗方法的若干研究[D]. 杭州: 浙江大学理学院, 2003: 3-5.
[2] 杜绍洪. 高维积分的新型求积公式[D]. 成都: 四川大学数学学院, 2004: 11-15.
[3] Morokoff W J, Caflisch R E. Quasi-random Sequences and Their Discrepancies [J]. SIAM J SCI Comput, 1994, 15(6):1251-1279.
[4] Niederreiter H. Random Number Generation and Quasi Monte Carlo Methods [M]. Philadelphia: SIAM, 1992: 10-21.
[5] Morohosi H, Fushimi M. A Practical Approach to the Error Estimation of Quasi-Monte Carlo Integrations [EB/OL]. [2012-01-08]. http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.37.9396&rep=rep1&type= pdf.
[6] Krykova I. Evaluting of Path-dependent Securities with Low Discrepancy Methods [D]. Massachusetts: Worcester Polytechnic Institute, 2003: 7-30.
[7] Brandimarte Paolo. Numerical Method in Finance: A MATLAB-based Introduction [M]. New York: John Wiley and Sons, 2002: 265-280.
[8] 宫野. 计算多重积分的蒙特卡罗方法与数论网格法[J]. 大连理工大学学报, 2001, 41(1): 21-22.
[9] Wang X Q, Fang K T. The Effective Dimension and Quasi-Monte Carlo Integration [J]. J Complexity, 2003, 19(2): 101-124.
Quasi Monte Carlo Method for Calculating Multiple Integrals
ZHANG Tao, ZHOU Zhongli, AN Suzhen, ZHANG Jun
(Key Laboratory of Mathematical Geology of Sichuan Province, Chengdu University of Technology, Chengdu, China 610059)
Basic principles of Quasi Monte-Carlo method for calculating multiple integrals were introduced. The uniformities of Halton sequences and of sequences produced by the Rand function were compared then. Later, steps, examples, and computer program written in MATLAB language of Quasi Monte- Carlo method for calculating multiple integrals were given. The effectiveness, accuracy and superiority of the proposed Quasi Monte- Carlo method could be fully demonstrated by examples.
Quasi Monte-Carlo Method; Halton Sequence; Multiple Integral
O242
A
1674-3563(2012)05-0033-06
10.3875/j.issn.1674-3563.2012.05.006 本文的PDF文件可以从xuebao.wzu.edu.cn获得
(编辑:王一芳)
2011-12-16
张涛(1986- ),男,河南信阳人,硕士研究生,研究方向:数学计算方法

