船舶推进轴系纵振动力吸振器设计及参数影响规律研究
杨志荣,秦春云,饶柱石,塔 娜
螺旋桨推进是船舶和水下航行器的主要推进方式。船舶在水中运动,不可避免地在艉部形成不均匀的伴流场;螺旋桨在不均匀伴流场中工作会产生脉动推力,经推进轴系、推力轴承及其基座传递到壳体,引起壳体产生振动,进而形成水下声辐射[1-2]。在减小轴系纵向振动的一系列措施[3]中,加装动力吸振器是有效且可行的方法。
Goodwin[4]首先分析使用共振改变器(Resonance Changer)控制螺旋桨轴承力对船体激励的可行性。澳大利亚学者Dylejko[5]基于四端参数法和传递功率流研究了安装轴系共振改变器(Resonance Changer)的降噪效果,其共振改变器串联安装在推力轴承与基座之间,并进一步研究了共振改变器的参数优化设计问题。刘耀宗[2]的研究建立在Dylejko的基础上,并以Dylejko的算例参数为对象,分析了动力吸振器的吸振效果,但未涉及到动力吸振器的实际布置方案。李良伟[6]在Goodwin的船舶轴系纵向振动模型上进行简化,对轴系采用集中质量和弹簧刚度进行等效替换,运用动力谐调消振理论,对两自由度集中质量主从系统的动力减振器进行参数优化设计,但未能考虑到实际情况下轴系是弹性连续体,同时未能涉及到动力减振器的结构形式及安装布置方案。
由于实际工作情况下往往希望既要实现对船舶轴系的减振同时又要求对轴系的结构改动最小,本文提出一种并联安装在船舶轴系上的动力吸振器的设计方法,其中船舶轴系与动力吸振器构成主从系统,实现振动能量在主系统上发生转移,实现抑制主系统共振的目的;考虑了船舶轴系作为弹性连续体的情况下,采用模态截取和模态综合法建立其轴系-动力吸振器混合动力学系统模型,对动力吸振器设计参数的影响规律进行分析。
1 船舶轴系-动力吸振器混合动力学建模
如图1所示,动力吸振器在船舶轴系中的安装布置,其中船舶轴系主要由螺旋桨、桨轴、中间轴、法兰、推力轴、推力轴承及其基座组成,这里将螺旋桨及其附连水简化为集中质量M,推进轴等效为一根具有分布质量和弹性的匀质轴,推力轴承和基座的纵向总刚度用等效线性弹簧刚度K代替,动力吸振器简化为质量为ma,纵向刚度为ka,阻尼为ca的质量弹簧阻尼系统,简化后的船舶轴系-动力吸振器混合动力学模型如图2所示。
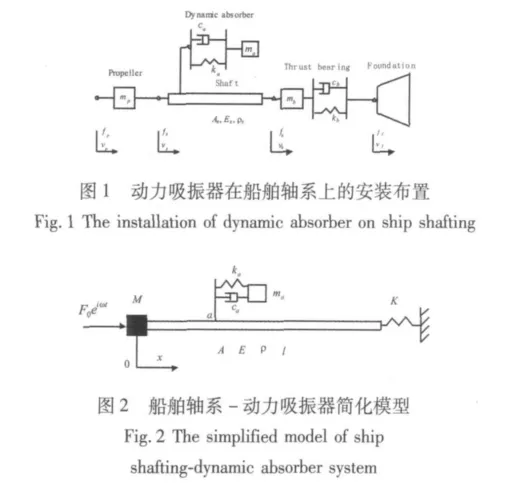
1.1 船舶轴系纵向振动固有频率及模态分析
由图2可知,当未安装动力吸振器时其船舶轴系的纵向振动响应解为[7]:
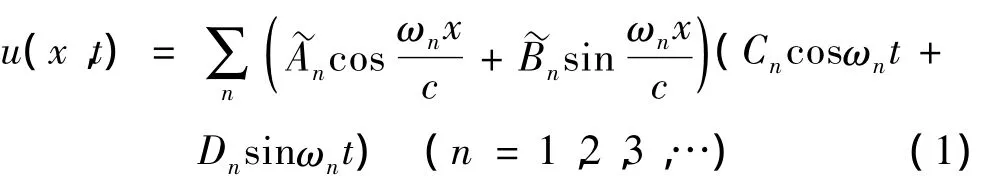
为各阶振型函数,
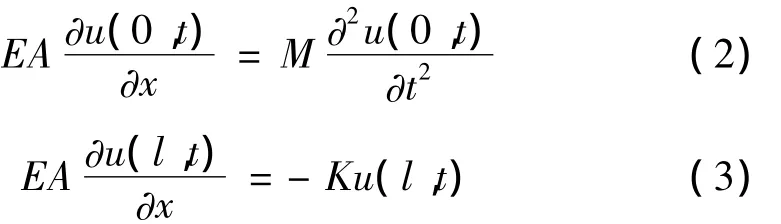
由式(2)可得:
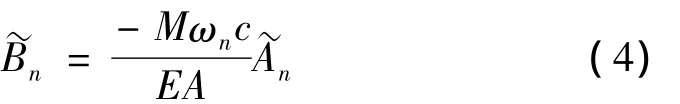
由式(3)可得:
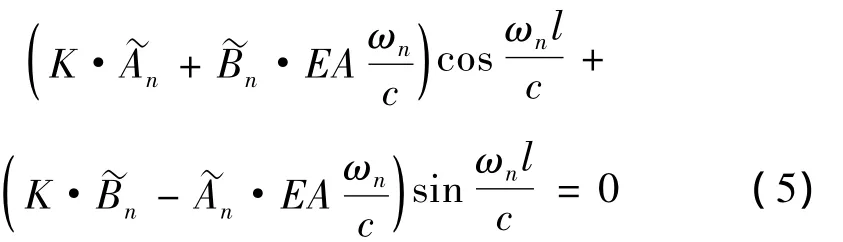
将式(4)代入式(5)得:
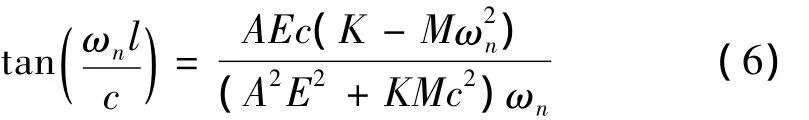
由式(6)求解出各阶固有频率后,再代入到式(1)中的振型函数Xn(x)表达式就可求得各阶振函数的精确解。
这里取各计算参数为:轴材料密度:ρ=7 850 kg/m3,轴材料弹性模量:E=1.96×1011Pa,轴系长度 l=13.5 m,轴外径 D=0.29 m,轴内径 d=0.165 m,螺旋桨及附连水质量M=7 760 kg,推力轴承及基座纵向总刚度K=1×1010N/m。根据式(6)的固有频率方程在MATLAB中进行编程求解,求得的各阶固有频率的解析解如表1所示。
为了验证理论推导的准确性,在有限元软件ANSYS中,采用BEAM188/MASS21/CONBIN14等单元建立其相应参数的船舶轴系有限元模型,计算出船舶轴系纵向振动前6阶固有频率值与由MATLAB编程求解式(6)固有频率方程的解,两者的比较如表1所示;由表1可知,两者的求解结果基本一致,特别是在前四阶中低频段吻合得较好,在高频段误差在3%以内,这是由于式(6)为超越方程,采用迭代方法求根,在高频段求解精度有影响,同时ANSYS中由于单元网格划分数的限制,其数值解本身的精度也受到影响。由此可以验证本文推导的船舶轴系纵向振动的固有频率方程及振型函数求解是正确的。
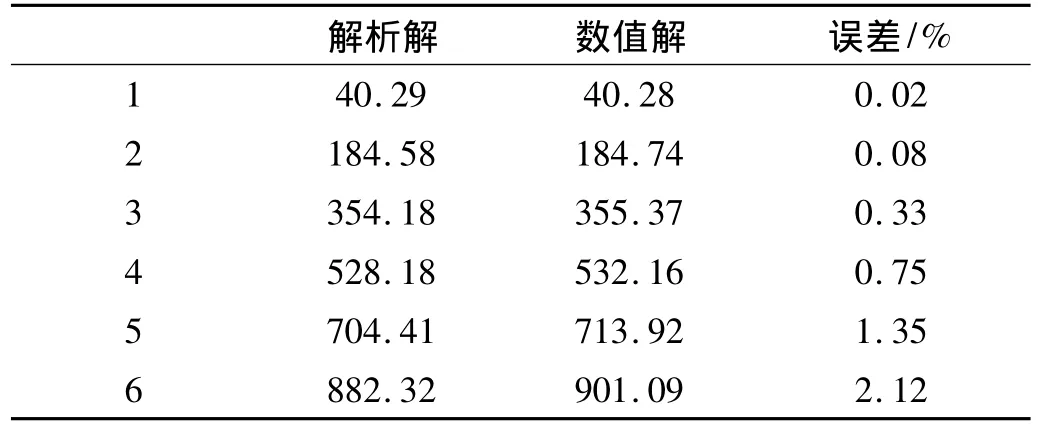
表1 前6阶固有频率解析解与ANSYS数值解结果比较(单位:Hz)Tab.1 The calculation of nature frequencies by analytic method and FEM
振型函数的正交性[7]:
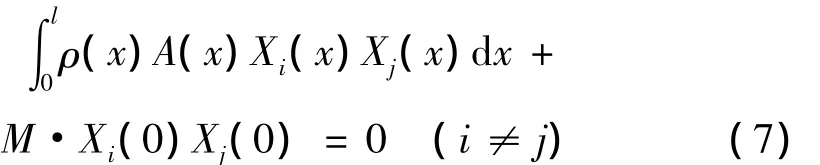
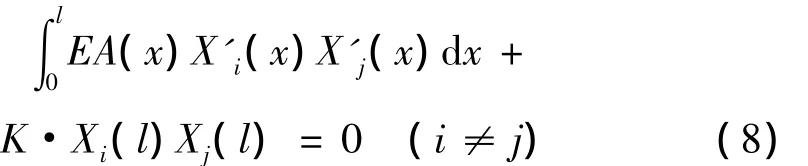
各阶主质量:
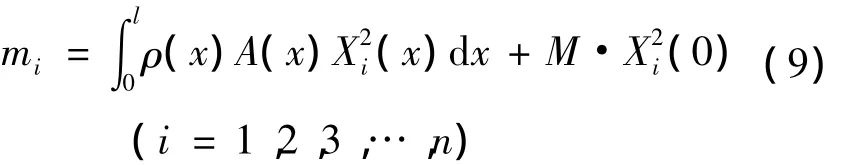
各阶主刚度:
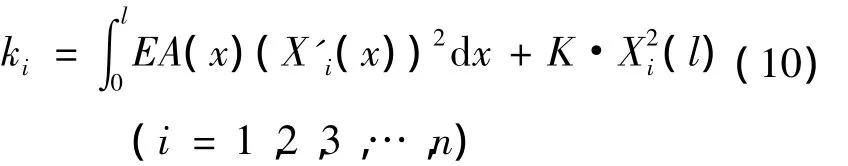
各阶固有频率:

1.2 模态截取及模态综合
弹性连续体的模态截取主要根据与激励频率相近的弹性体模态振型为主要振型,一般截取1阶主振型与动力吸振器子结构进行模态综合都能较好地给出动力吸振的近似解[8]。一般情况下船舶轴系正常工作转速为50~400 r/min之间,假定螺旋桨的桨叶为7叶,其螺旋桨脉动推力激励频率主要为叶频,范围为6~47 Hz之间,主要激起船舶轴系的第一阶模态,因此,这里截取船舶轴系的第一阶模态振型函数与动力吸振器进行模态综合,构建船舶轴系-动力吸振器混合动力学模型。
安装动力吸振器后的力学模型表示于图2。动力吸振器的安装部位在x=a点,船舶轴系在螺旋桨处(x=0)承受的纵向集中力为 F0eiωt,是频率为ω的简谐力。耦合动力吸振器后全系统的动能和弹性势能分别为T和U,其解析式为:
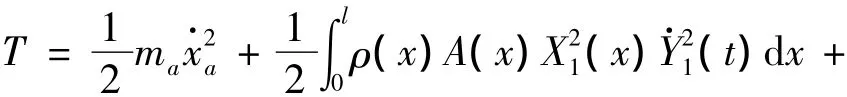
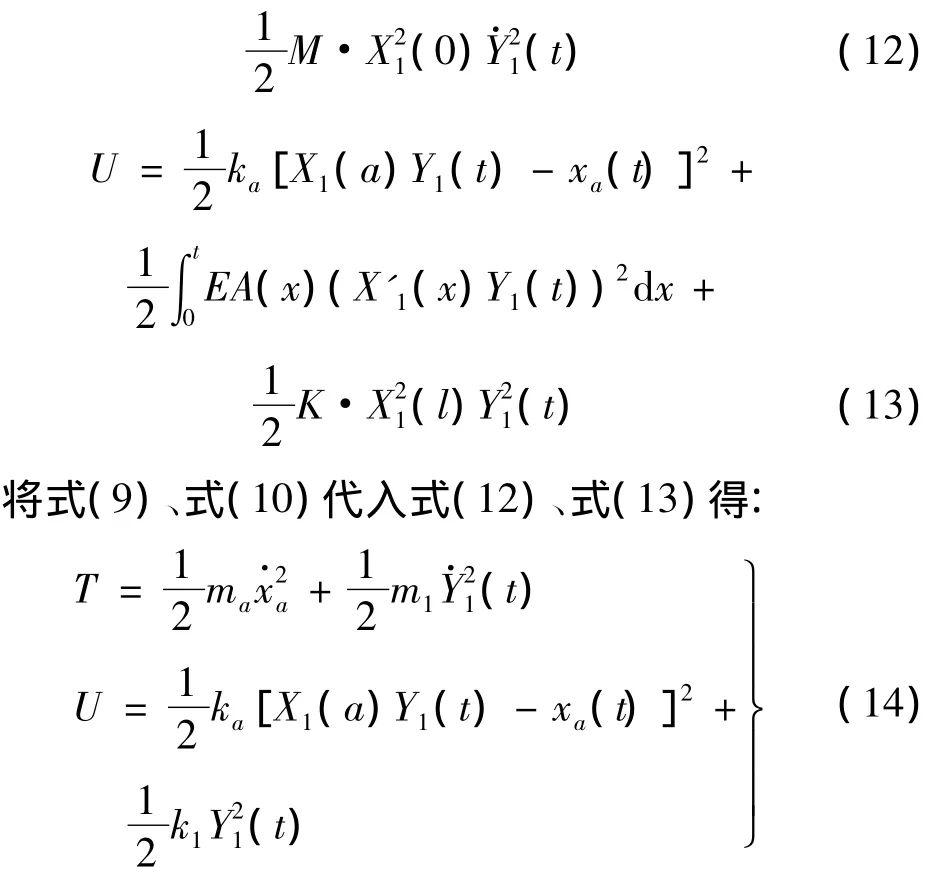
由拉格朗日方程推导出全系统的运动方程,将其写成矩阵形式:
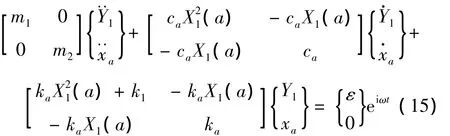
式中:ε表示作用在螺旋桨处(x=0)纵向集中力强度的常数,其大小为:
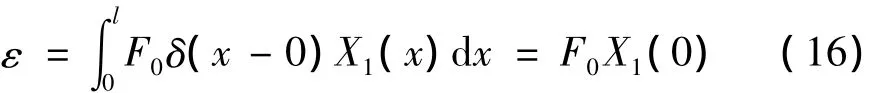
由式(15)可知,对于均质直弹性轴而言,如果只考虑它的第一阶主振型,那么,它的动力吸振问题就相当于主质量为m1的单自由度振动系统受到集中力εeiωt激励时的动力吸振问题。
将式(15)拉氏变换后,用iω代替s,可以导出广义坐标 Y(t)对广义力 εeiωt的传递函数 R(ω):
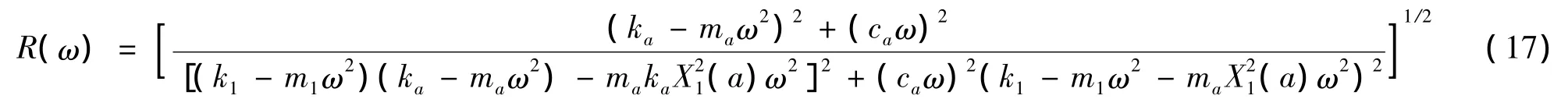
定义以下的无量纲参数[8]:
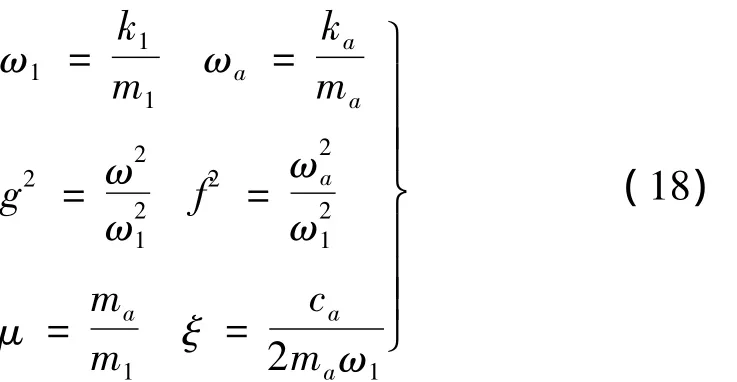
式中:g为频率比,f为固有频率比,μ为质量比,ξ为阻尼比。由此可以写出船舶轴系任意截面第一振型的振幅的近似解析式:
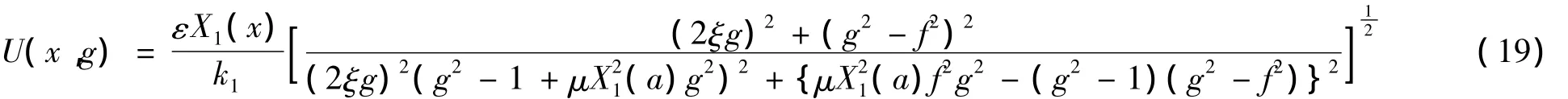
进一步可以求得传递到推力轴承基座上的力与激励力之间的力传递率(动力放大系数):
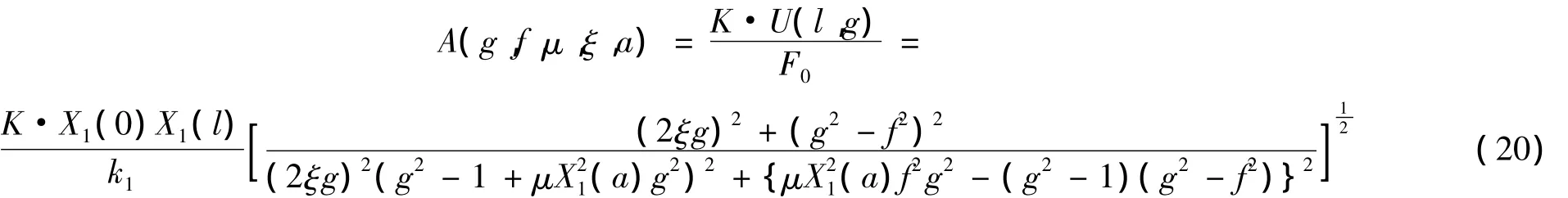
由式(20)可知,动力放大系数 A(g,f,μ,ξ,a)是频率比g,固有频率比f,质量比μ,阻尼比ξ,动力吸振器安装位置a的函数。
2 动力吸振器设计参数影响规律分析
2.1 质量比μ对动力放大系数的影响
取动力吸振器在轴上的安装位置a=2 m,固有频率比 f=1,阻尼比 ξ=0.1,讨论质量比 μ =0.01,0.05,0.1,0.2这4组取值时对动力放大系数的影响。相应的动力放大系数A(g)曲线如图3所示。由图可知,随着质量比的增大,在吸振频率附近两个共振峰向相反方向偏移,使得动力吸振器的吸振频带变宽,且在吸振频率附近传递到基座上的纵振激振力进一步降低,吸振效果越好。实际设计动力吸振器的质量时要综合考虑动力吸振器重力对轴系弯曲应力的影响,一般情况下取质量比 μ=0.03~0.05即可。
2.2 固有频率比f对动力放大系数的影响
取动力吸振器在轴上的安装位置a=2 m,质量比μ =0.05,阻尼比 ξ=0.1,讨论固有频率比 f=0.6,0.8,1,1.2这4组取值时对动力放大系数的影响。相应的动力放大系数A(g)曲线如图4所示。由图可知,在这组数据中,动力吸振器的固有频率比取f=1时,吸振效果最好。且随着固有频率比在f=1附近变化时,在吸振频率处的动力放大系数急剧变化,因此,必然在f=1附近存在一个最优固有频率比使得动力吸振器在吸振频率附近效果最好,吸振频带最宽。
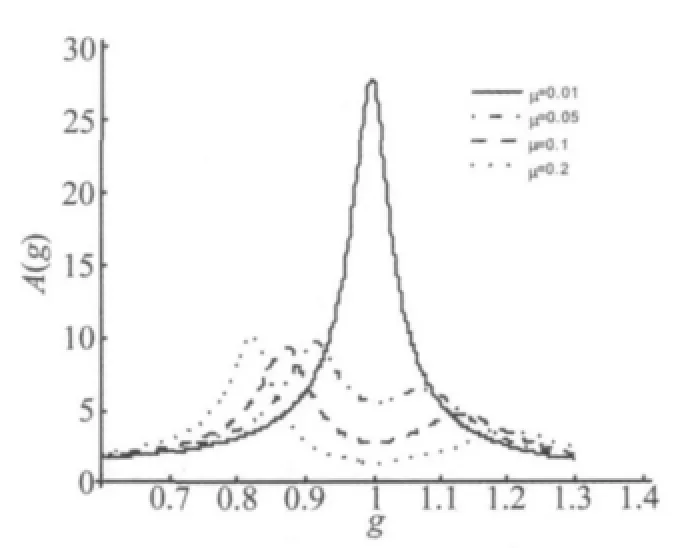
图3 质量比对动力放大系数的影响Fig.3 The effect of dynamic amplification by mass ratio
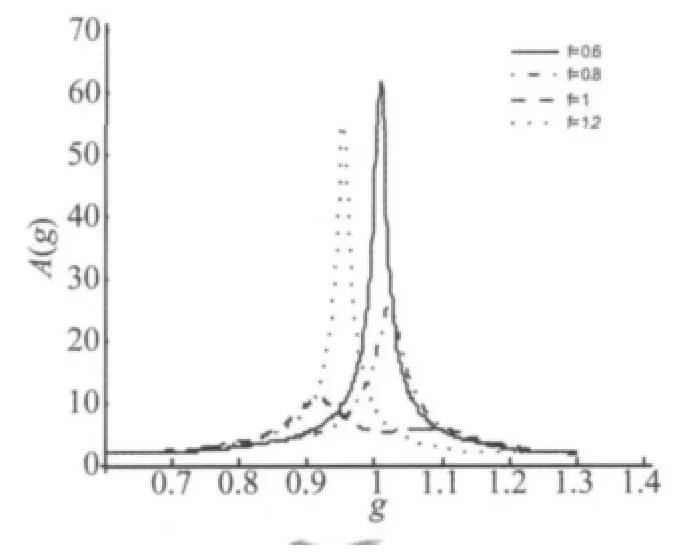
图4 固有频率比对动力放大系数的影响Fig.4 The effect of dynamic amplification by nature frequency ratio
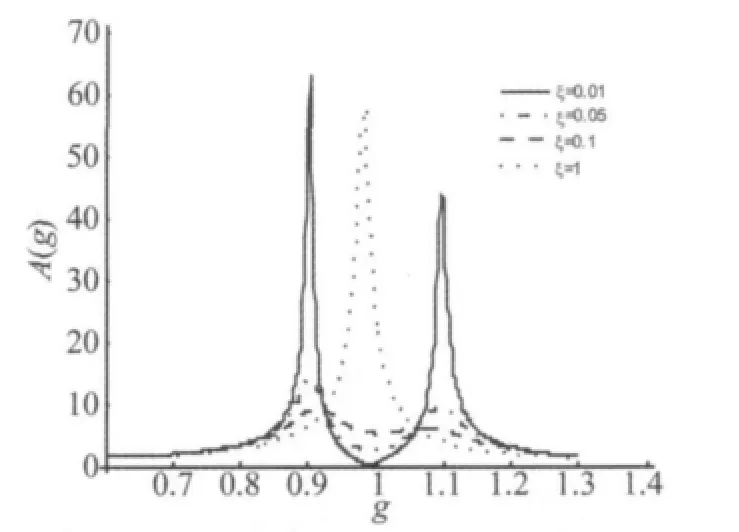
图5 阻尼比对动力放大系数的影响Fig.5 The effect of dynamic amplification by damp ratio
2.3 阻尼比ξ对动力放大系数的影响
取动力吸振器在轴上的安装位置a=2 m,质量比μ =0.05,固有频率比 f=1,讨论阻尼比 ξ=0.01,0.05,0.1,1这4组取值时对动力放大系数的影响。相应的动力放大系数A(g)曲线如图5所示。由图可知,在阻尼比ξ=0.01时,由螺旋桨传递到基座上的纵振激振力得到较大降低,但在吸振频率两侧出现个较大的峰值,这将影响结构整个频段力传递率的降低效果;随着阻尼比的增加,曲线变得圆滑,分布在吸振频率两侧的共振峰幅值有较大程度的降低,吸振频带变宽,但是在共振吸振频率处效果变差,因此频宽的增加是以牺牲共振吸振频率处的吸振效果为代价的,存在一个兼顾双方的最优阻尼比。当阻尼比为大阻尼时,在共振吸振频率附近,没有吸振效果,相当于动力吸振器与轴系固连在一起又变成单自由度系统。
2.4 动力吸振器安装位置对动力放大系数的影响
取动力吸振器的固有频率比 f=1,质量比 μ=0.05,阻尼比ξ=0.05,讨论动力吸振器在轴上的不同安装位置对动力放大系数的影响。图6为动力吸振器在不同安装位置下的动力放大系数的三维图。由图可知,吸振器的安装位置对轴系的纵向振动特性有较大的影响,通常应将动力吸振器安装在被减振结构振幅最大处,由上述轴系纵振模态分析可知,在轴系纵振第一阶共振频率时,靠近螺旋桨端的振动响应幅值最大,推力轴承端振动响应幅值最小。因此,为了使吸振器达到最好的吸振效果,消减轴系第一阶纵向振动时应该把吸振器尽量布置在轴系艉端。
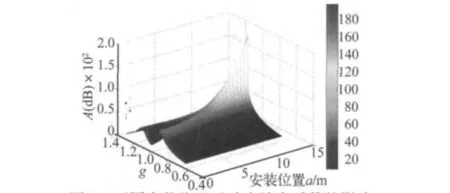
图6 不同安装位置对动力放大系数的影响Fig.6 The effect of dynamic amplification by different installation location
3 结论
本文提出一种并联安装在船舶推进轴系上的纵振动力吸振器的设计方法,采用模态截取和模态综合法建立其轴系-动力吸振器混合动力学系统模型,对动力吸振器设计参数的影响规律进行分析。主要结论如下:
(1)特殊边界条件下,轴系纵振的振型函数的正交性、主质量和主刚度具有和常规边界条件下的轴系纵振振型函数不同的表达式;
(2)弹性连续体的模态截取主要根据与激励频率相近的弹性体模态振型为主要振型。对于轴系的正常工作转速范围内,一般取轴系纵振第一阶模态振型进行综合,都能给出动力吸振较好的近似解;
(3)质量比取得越大,吸振效果越好,但应该综合考虑到吸振器重量对轴系弯曲应力的影响;
(4)固有频率比对吸振效果影响很大,在固有频率比等于1的附近存在着最优的固有频率比使得吸振效果和吸振带宽达到最优;
(5)阻尼比越小,在共振吸振频率处吸振效果越好,但是在吸振频率两侧出现个较大的峰值,频带变窄;大阻尼比下,在共振吸振频率处没有吸振效果;
(6)为了使吸振器达到最好的吸振效果,消减轴系第一阶纵向振动时应该把吸振器尽量布置在轴系艉端,即被减振结构振幅最大处。
[1]谢基榕,沈顺根,吴有生.推进器激励的艇体辐射噪声及控制技术研究现状[J].中国造船,2010,51(4):234-241.
[2]刘耀宗,王 宁,孟 浩,等.基于动力吸振器的潜艇船舶轴系轴向减振研究[J].振动与冲击,2009,28(5):184-187.
[3]许运秀,钟学添,何轩轩.船舶轴系纵向振动[M].北京:人民交通出版社,1985.
[4] Goodwin A.The design of a resonance changer to overcome excessive axial vibration of propeller shafting[J].Institute of Marine Engineers-Transactions,1960,72:37-63.
[5] Dylejko PG,Kessissoglou N J,Tso Y,et al.Optimisation of a resonance changer to minimise the vibration transmission in marine vessels[J].Journal of sound and vibration,2007,300(1-2):101-116.
[6]李良伟,赵 耀,陆 坡,等.减小船舶轴系纵向振动的动力减振器参数优化[J].中国造船,2010,51(2):139-148.
[7]季文美,方 同,陈松淇.机械振动[M].北京:科学 出版社,1987.
[8]丁文镜.减振理论[M].北京:清华大学出版社,1988.

