滚珠型弧面凸轮分度机构动力学模型建立及模态分析

李 蕾，冯显英，张成梁，牟世刚，王绥远

弧面分度凸轮机构的结构比较简单，能够实现多种运动规律，被广泛用于印刷、包装、食品等机械。当机构转速较低以及机构零件刚性足够大时，对机构进行运动学与静力学分析就能满足基本要求。但随着工业自动化的发展，对于高速机构，其动力学特性成为提高速度的主要制约，因此需要进行动力学分析。当前对弧面凸轮机构的研究较多地集中在弧面凸轮的几何特性分析［1－2］、建模仿真［3－4］以及加工方法上［5－6］，对弧面凸轮机构动力学的研究相对较少。天津大学［7－8］对圆柱滚子弧面凸轮机构做了比较深入的研究，但对于滚珠型弧面凸轮机构动力学［9］研究得非常少。本文对一种新型滚珠型弧面凸轮分度机构中的接触刚度进行了分析，并且在建模过程中分析了广义坐标微小位移间的几何关系，建立了考虑弹性扭转模量的动力学方程。

1 滚珠型弧面凸轮分度机构结构介绍

如图1所示，滚珠型弧面凸轮分度机构主动件是弧面凸轮，弧面凸轮滚道为双圆弧截形，从动件是分度盘，分度盘由三个零件组合而成(如图2所示)。在此机构运动过程中，滚珠作为媒介传递力和运动，滚珠与凸轮为一点接触，滚子与分度盘为两点接触。

图1 滚珠型弧面凸轮分度机构Fig.1 Globoidal cam indexing mechanism with steel ball

图2 分度盘Fig.2 Indexing plate

2 等效接触刚度分析

2.1 Hertz接触理论

根据赫兹理论，两个弹性体之间的压力分布呈半椭圆形，接触面在切面上将有一个椭圆边界［11］。椭圆边界短轴b的方程式为:

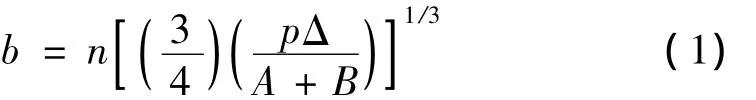
式中:n为接触椭圆常数，通过求得θ角度的值，然后查接触椭圆常数表求得。θ方程为:

式中:

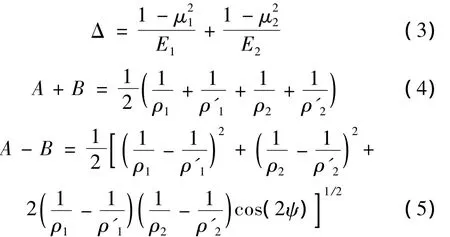
式中:P为接触面上相互作用的正压力，ρ1，ρ2为接触点的最小曲率半径，ρ1'，ρ2'为最大曲率半径，μ1，μ2为两种材料的泊松比，E1，E2为两种材料的弹性模量，ψ为最大曲率所在平面间的夹角。

滚珠的压缩深度为:

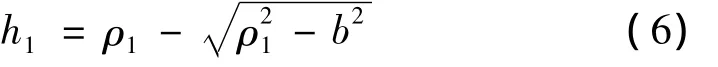
与滚珠接触零件的压缩深度为:

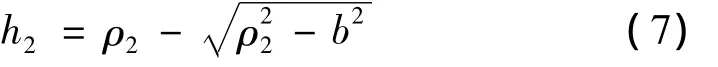
2.2 滚珠与凸轮之间的Hertz接触刚度

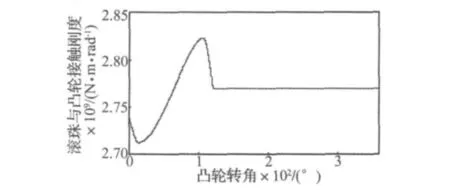
图3 滚珠与凸轮之间的变形刚度变化曲线Fig.3 Contact stiffness between roller and globoidal cam

滚珠与凸轮之间的Hertz接触刚度即变形刚度与接触曲率有密切的关系，凸轮的接触曲率在分度段随着凸轮转角的变化而变化，因此变形刚度也是在不断变化的。分别求出滚珠和凸轮接触点上的压缩深度h1，h2，得到滚珠与凸轮之间的变形刚度为 k1c=本文中凸轮与滚珠的材料相同，弹性模量和泊松比分别取值为210 GPa和0.28，凸轮运动曲线为修正正弦曲线。得到了图3所示的滚珠和凸轮之间的变形刚度变化曲线。

2.3 滚珠与分度盘之间的Hertz接触刚度

滚珠与分度盘上有两个接触点，其中分度盘中间圆盘上的接触点为主要受力点。因此本文中将滚珠与分度盘中间圆盘上接触点的变形刚度作为滚珠与分度盘之间的变形刚度计算。滚珠的最大曲率和最小曲率相等，为滚珠半径的倒数;分度盘的最大曲率为分度盘中间圆盘凹槽圆弧半径的倒数，最小曲率为零。分别求出滚珠和分度盘接触点的压缩深度h1'、h2'，得到滚珠与分度盘之间的变形刚度为滚珠的半径为14 mm，凹槽圆弧半径为15 mm，得到滚珠与分度盘之间的变形刚度为1.578×108N·m/rad。

在无润滑情况下，滚珠与凸轮以及分度盘之间的摩擦为干摩擦，接触刚度为变形刚度，当在接触副中存在润滑时，接触刚度由变形刚度和油膜刚度组成。根据文献［12］中的接触中心区的油膜厚度得到了滚珠与凸轮间的油膜刚度k1f以及滚珠与分度盘之间的油膜刚度k2f。滚珠与凸轮之间的接触刚度k1可以认为是变形刚度和油膜刚度的串联，同样滚珠与分度盘之间的接触刚度k2也为变形刚度和油膜刚度的串联。

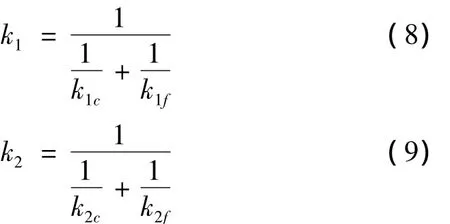
2.4 等效接触刚度

在动力学建模中，由于滚珠相对凸轮和分度盘质量较小，可以忽略。如图4所示滚珠与凸轮之间的接触刚度以及滚珠与分度盘之间的接触刚度可以近似看作串联［10］。串联后的刚度为:

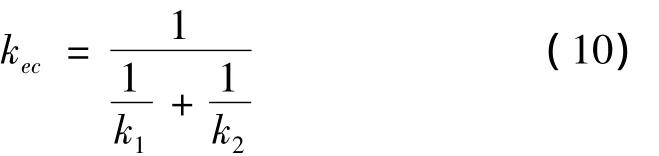
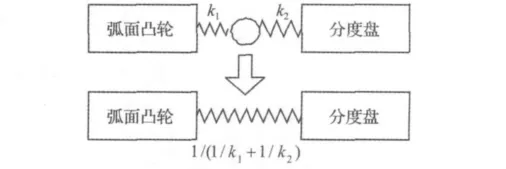
图4 接触副间的等效接触刚度Fig.4 Equivalent contact stiffness for contact pair

由已得到的滚珠与凸轮之间的接触刚度和滚珠与分度盘之间的接触刚度，代入式(10)得到等效接触刚度如图5所示。

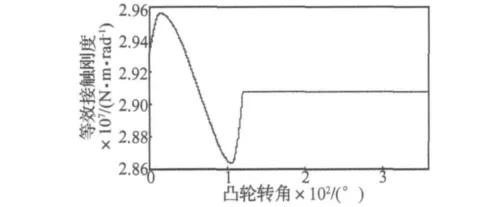
图5 等效接触刚度随凸轮转角的变化曲线Fig.5 Variation curve for equivalent contact stiffness

3 动力学方程的建立

3.1 动力学模型与符号说明

弧面凸轮机构中的扭转是传递运动的主要方式，本文假定滚珠与凸轮以及分度盘之间可实现无间隙啮合运动，阻尼很小可以忽略，主要考虑机构的扭转弹性模量，建立了弧面凸轮机构的动力学模型。图6为弧面凸轮分度机构动力学模型简图。

图6 弧面凸轮分度机构力学模型简图Fig.6 Dynamic model for globoidal cam indexing mechanism

模型中，J1为载荷盘的转动惯量，J2为分度盘的转动惯量，J3为弧面凸轮的转动惯量，φ为凸轮轴理论转角，τ(φ)为分度盘理论转角，φ1为载荷盘转角，φ2为分度盘转角，φ3为弧面凸轮转角，kφ1为输出轴的扭转刚度，kφ3为输入轴的扭转刚度，kec为等效接触刚度。

3.2 广义坐标几何位移关系分析

凸轮、滚珠以及分度盘之间的位置是一种空间的相对位置关系，比较复杂，如图7所示。本文采用了回转变换张量法将凸轮及分度盘的微小角位移转化到接触点的法线方向上。图中K1点为滚珠与分度盘的接触点，K2点为滚珠与凸轮之间的接触点。由于两接触点的法线方向不在同一条直线上，根据受力情况，本文统一把微小角位移转化在K2点法线方向上。符号rk1表示K1点到分度盘中心的半径，lf表示分度盘半径，c表示中心距，θ1表示分度盘转角，γ表示螺旋升角。

微小角位移δ(φ2)，转化到Y1＇轴上的位移近似为rk1×δ(φ2)，转化到K2点法线方向上的微小位移为:

微小角位移δ(φ3)，在Z轴方向上的位移近似为(c－lfcosθ1)δ(φ3)，转化到 K2点法线方向上的微小位移为:

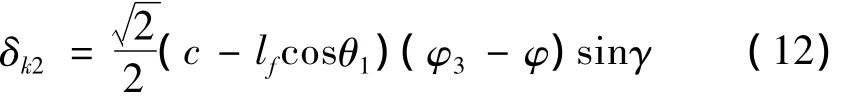
因此总位移为 δ=δk1－δk2。

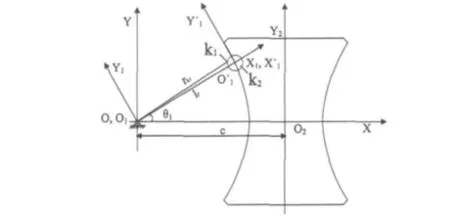
图7 弧面凸轮机构零件的相对位置及运动变换关系Fig.7 Relative position and relationship of motion conversion for components of globoidal cam indexing mechanism

3.3 动力学方程的建立

拉格朗日方程是从能量的角度求得动力学方程，本文应用拉格朗日方程推导凸轮传动系统的动力学方程如下:

弧面凸轮机构系统的动能:

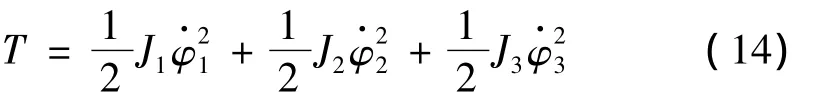
弧面凸轮机构系统的势能:

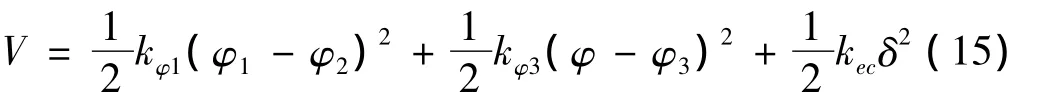
应用拉格朗日方程得到弧面凸轮机构的动力学方程如下:

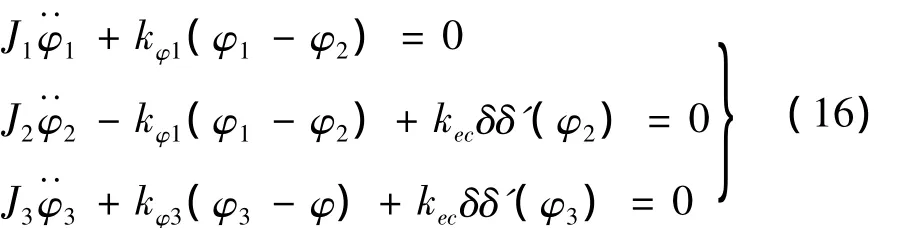
因为机构组成的各零部件有几何加工误差和装配误差，滚珠和凸轮之间很可能存在间隙。假定在滚珠与凸轮作用点 K2法线方向上有间隙 ξ时，根据Dubowsky冲击间隙模型，得到接触刚度系数为:

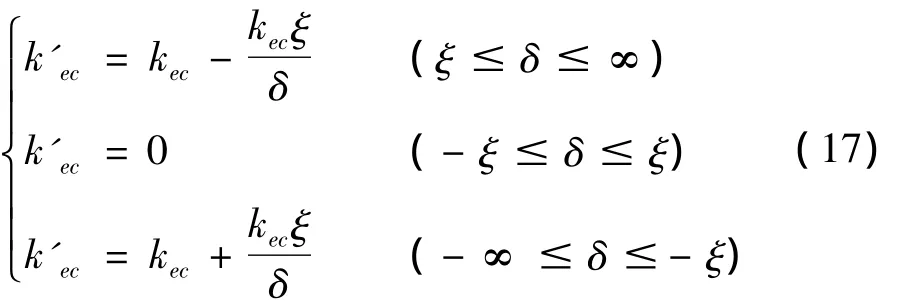
4 固有频率及振型的计算

由动力学方程组(16)求得了系统的固有频率及其相对应的阵型。系统的刚度矩阵在分度段时随着凸轮转角的变化而改变，因此系统的固有频率是不断变化的，在分度段时期固有频率对应阵型也是在变化的。为了方便，这里求得了停歇期固有频率对应的阵型。刚度矩阵为:

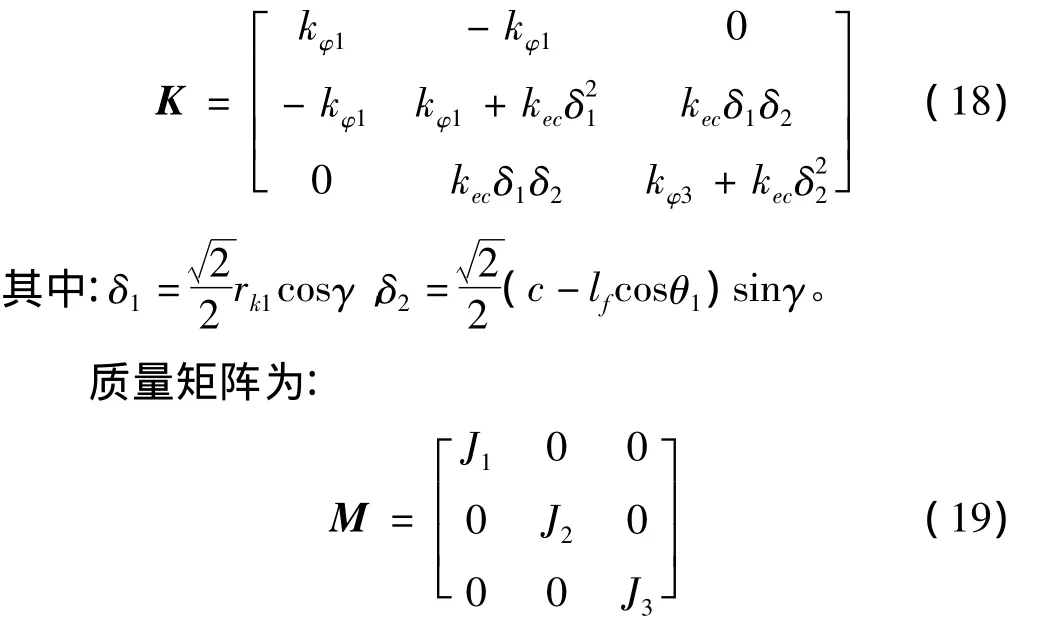
凸轮转角在0°～120°为分度期，图8为固有频率变化曲线图，可以看到分度期间的固有频率是变化的，停歇期间的固有频率是恒定值，不同阶固有频率的变化曲线趋势并不相同，其中由图8(a)可以看到第一阶频率在分度期中间位置的频率为最低。外界激励频率应避开固有频率，以免引起共振。图9为机构停歇期间固有频率对应的振型图，图中的横坐标1，2和3分别代表凸轮传动系统中的广义坐标φ1，φ2和φ3，字符代表意义同上。图9(a)第一阶振型表现为载荷盘的扭振，图9(b)第二阶振型表现为分度盘和凸轮都有扭振，且凸轮的扭振程度大于分度盘。表1是求解过程中用到的部分参数。

表1 部分计算参数Tab.1 Partial calculation parameters

5 结论

本文对一种新型滚珠型弧面凸轮分度机构进行了动力学建模。首先分析了在有润滑和无润滑情况下滚珠与凸轮以及滚珠与分度盘之间的接触刚度，由于滚珠质量较小，忽略滚珠的质量得到了等效接触刚度。在建模过程中，根据机构中各零件的相对位置及运动关系，用回转变换张量法分析了广义坐标微小位移的几何关系。考虑机构的扭转弹性模量建立了动力学方程，得到了机构的固有频率和停歇期间固有频率对应的振型。通过固有频率变化曲线可以看到分度期间的固有频率是变化的，停歇期间的固有频率是恒定值，不同阶的固有频率变化趋势也不相同。外界激励频率应尽量避免与固有频率相同，以免引起共振。

［1］方代正，李素荣.新型弧面凸轮分度机构的压力角分析［J］.煤矿机械，2006，27(4):601 －603.

［2］杨 玮，曹巨江.复杂弧面凸轮曲率和应力分析及其CAD［J］.设计与研究，2002，31(2):11－13.

［3］李 蕾，冯显英，张紫平，等.钢球滚子弧面分度凸轮机构的三维建模及运动仿真［J］.机床与液压，2010，38(21):102－104.

参考文献

［4］Yan H S，Chen H H.Geometry design of roller gear cams with hyperboloid rollers［J］.Mathl.Comput.Modelling，1995，22(8):107－117.

［5］葛荣雨，冯显英，王庆松.弧面凸轮廓面非等径加工的刀位控制方法［J］.农业机械学报，2010，41(9):223－226.

［6］窦湘屏，袁光明，刘 磊.五轴联动加工中心加工弧面凸轮［J］.机械制造与研究，2010，39(6):45 －48.

［7］贺 炜，彭国勋，胡亚平，等.弧面分度凸轮机构传动系统非线性动力学研究［J］.机械工程学报，2000，36(11):33－37.

［8］常宗瑜，张 策，杨玉虎，等.含间隙弧面分度凸轮机构动力学的实验研究［J］.机械强度，2006，28(2):173－177.

［9］苗 苗，陶学恒.球形滚子弧面凸轮分度机构模态分析［J］.大连轻工业学院学报，2005，24(4):286 －288.

［10］赵联春.球轴承振动的研究［D］.杭州:浙江大学，2003.

［11］彭国勋，肖正扬.自动机械的凸轮机构设计［M］.北京:机械工业出版社，1990.

［12］付振山，冯显英，李 蕾，等.钢球滚子弧面分度凸轮的弹流润滑分析［J］.农业机械学报，2011，42(6):208 －212.