一类广义BBM-Burgers方程的Cauchy问题

张能伟， 陈翔英

(1.安阳师范学院 数学与统计学院 河南 安阳 455002； 2.郑州电力高等专科学校 经济贸易系 河南 郑州 450004)

0 引言

文[1]研究了具有耗散项的多维广义BBM-Burgers方程组Cauchy问题

(1)

u(x,0)=u0(x),x∈RN

(2)

文[2]证明了具有耗散项的一维广义BBM-Burgers方程组Cauchy问题

ut+f(u)x-αuxxt-βuxx+γuxxxx=0,x∈R,t>0,

(3)

u(x,0)=u0(x),x∈R

(4)

整体光滑解的存在性和收敛性，其中，α,β,γ>0为常数，u(x,t)=(u1(x,t),…,un(x,t))T和f(u)=(f1(u),…,fn(u))T为光滑向量值函数.文[3]研究了多维的Cauchy问题(3)，(4)整体光滑解的存在性和收敛性，所得结果推广了Cauchy问题(3)，(4)的结果.

作者研究下列广义BBM-Burgers方程的Cauchy问题

vt-αvxxt-βvxx+γvxxxx+f(v)x=G(v)+h(vx)x+g(v)xx,x∈R,t>0,

(5)

v(x,0)=v0(x),x∈R,

(6)

作者采用以下记号：Lp(1≤p≤∞)表示所有定义在R上Lp可积函数的空间，并赋予范数‖·‖Lp=

1 Cauchy问题(5),(6)局部解的存在性和唯一性

为了讨论方便起见，对方程(5)和初值条件作尺度变换

(7)

于是方程变为

(8)

则Cauchy问题(5)，(6)变为

ut-uxxt-uxx+uxxxx+f(u)x=G(u)+h(ux)x+g(u)xx,x∈R,t>0,

(9)

u(x,0)=u0(x),x∈R.

(10)

所以作者只需研究Cauchy问题(9)，(10)整体强解和整体古典解的存在性、唯一性和解的衰减性质，因为通过变换(7)可得Cauchy问题(5)，(6)的结果.

为了将Cauchy问题(9)，(10)转化为积分方程，引入常微分方程的基本解和几个引理.令F(x)是常微分方程

w(x)-wxx(x)=δ(x)

(11)

引理1①F(x)在R上有意义、连续且F(x)>0;

②F(x)∈Lq,其中，1≤q≤∞且‖F‖1=1；

④‖F*f‖Hs(R)=‖f‖Hs-2(R),∀s∈R,其中，F*f(x)表示函数F和f的卷积.

引理2[4]假设f(u)∈Ck(R),f(0)=0,u∈L∞∩Hs(R)且k=[s]+1,s≥0.如果‖u‖L∞(R)≤M,则

‖f(u)‖Hs(R)≤C1(M)‖u‖Hs(R),

其中，C1(M)是依赖于M的常数.

引理3[5]假设s≥0,f(u)∈Ck(R)(k=[s]+1),u,v∈L∞∩Hs(R),如果‖u‖L∞(R)+‖u‖Hs(R)≤M,‖v‖L∞(R)+‖v‖Hs(R)≤M,则

‖f(u)-f(v)‖Hs(R)≤C2(M)‖u-v‖Hs(R),

其中，C2(M)是依赖于M的常数.

设u(x,t)∈C1([0,T];Hs(R))(s≥4)是问题(9)，(10)的强解，则方程(9)可写为

ut-uxx-[ut-uxx]xx+f(u)x=G(u)+h(ux)x+g(u)xx.

(12)

令f(0)=h(0)=g(0)=G(0)=0,由方程(12)和基本解F(x)可知

(13)

定义1对于任意T>0，如果s≥2,函数u(x,t)∈C([0,T);Hs(R))∩C1([0,T);Hs-2(R))是问题(13)，(10)的解，则称u(x,t)是问题(9)，(10)的强解.如果T<∞，则称u(x,t)为问题(9)，(10)的局部强解;如果T=∞,则称u(x,t)为问题(9),(10)的整体强解.

为了应用压缩映射原理证明问题(13),(10)存在唯一的整体解,首先考虑下列线性方程的Cauchy问题

ut-uxx=φ(x,t), (x,t)∈R×[0,T],

(14)

u(x,0)=u0(x),x∈R.

(15)

引理4令s∈R.设对任意的T>0，u0∈Hs(R),φ∈L1([0,T];Hs(R)),则问题(14)，(15)存在唯一强解u(x,t)∈C([0,T];Hs(R))且有估计

(16)

证明类似于文献[6],证明波动方程的Cauchy问题

utt-uxx=φ(x,t), (x,t)∈R×[0,T],

u(x,0)=u0(x),ut(x,0)=u1(x),x∈R

解的存在唯一性，可以证明问题(14)，(15)存在唯一的强解u(x,t)∈C([0,T];Hs(R)).下面证明估计式(16)成立.方程(14)两边作Fourier变换，有

(17)

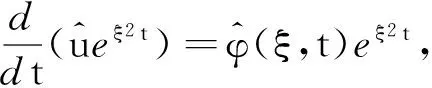
(18)

(19)

引理证毕.

对于s≥2,u0∈Hs(R),定义函数空间X(T)={w|w∈C([0,T];Hs(R))},其范数定义为

显然X(T)是一个Banach空间.对于任意M，T>0,定义集合

P(M,T)={w|w∈X(T),‖w‖X(T)≤M},

显然P(M，T)是X(T)中一不空有界闭凸集，对于w∈X(T)，u0∈Hs(R),g,f,h,G∈Ck(R)且k=[s]+1，考虑下列线性方程的Cauchy问题

ut-uxx=F*[G(w)+h(wx)x-f(w)x+g(w)xx],x∈R,t>0,

(20)

u(x,0)=u0(x),x∈R.

(21)

令S表示由w到问题(20)，(21)的唯一解的映射，由引理4知，S映X(T)到X(T).

定理1设u0∈Hs(R)(s≥2),g,f,h,G∈Ck(R),f(0)=g(0)=h(0)=G(0)=0且k=[s]+1.如果T相对于M充分小，则S：P(M，T)→P(M，T)是严格压缩的.

证明当s≥2时，由Sobolev嵌入定理推得

由引理1和引理2得

(22)

所以由引理4知

(23)

如果M和T满足

(24)

则由(23)式推出‖u(·,t)‖Hs(R)≤M.因此，如果(24)式成立，则S映P(M，T)到P(M，T).下证S:P(M,T)→P(M,T)是严格压缩的.

给定w1,w2∈P(M,T).令u1=Sw1,u2=Sw2,u=u1-u2,w=w1-w2,则u(x,t)满足下列Cauchy问题

ut-uxx=F*[G(w1)-G(w2)+h(w1x)x-h(w2x)x-

(f(w1)x-f(w2)x)+g(w1)xx-g(w2)xx],x∈R,t>0,

(25)

u(x,0)=0,x∈R.

(26)

由引理1和引理3推出

‖F*[f(w1)x-f(w2)x]‖Hs(R)≤‖f(w1)-f(w2)]‖Hs-1(R)

(27)

类似可知

(28)

(29)

(30)

所以由引理4和(27)～(30)式有

(31)

如果T满足(24)式和

(32)

定理2设u0∈Hs(R)(s≥2),g,f,h,G∈Ck(R),f(0)=g(0)=h(0)=G(0)=0且k=[s]+1，则Cauchy问题(9)，(10)存在唯一的局部强解u(x,t)∈C([0,T0);Hs(R))∩C1([0,T0);Hs-2(R)),其中，[0，T0)是解存在的最大时间区间，同时如果

(33)

则T0=∞.

证明由定理1和压缩映射原理知，对于适当选择的T>0,S有唯一不动点u(x,t)∈P(M,T),显然它是问题(9)，(10)的局部广义解，易证对于每一T′>0,问题(9)，(10)至多有一解u∈X(T′).

下面证明u∈C1([0,T0);Hs-2(R)).由方程(13)和引理1，2推出

所以Cauchy问题(9)，(10)存在唯一强解u∈C([0,T0);Hs(R))∩C1([0,T0);Hs-2(R)).

令[0，T0)是解u∈X(T0)存在的最大时间区间，利用文献[7]中的标准方法可证如果(33)式成立，则T0=∞.定理证毕.

下面将解的延拓条件(33)转化为以下定理3中的(34)式.

定理3设u0∈Hs(R)(s≥2),g,f,h,G∈Ck(R),f(0)=g(0)=h(0)=G(0)=0且k=[s]+1，又设[0，T0)是问题(9)，(10)解u(x,t)存在的最大时间区间，如果

(34)

则T0=∞.

证明由(34)式可知‖u(·,t)‖L∞(R)<λ,t∈[0,T0).令

由引理1和引理2得

≤C1(λ)‖u‖Hs-2(R)+C1(λ)‖ux‖Hs-1(R)+C1(λ)‖u‖Hs-1(R)+C1(λ)‖u‖Hs(R)

≤4C1(λ)‖u‖Hs(R)=C5(λ)‖u‖Hs(R).

由引理4推出

2 Cauchy问题(9) ，(10)的整体解

为了证明问题(9)，(10)存在唯一的整体强解和整体古典解，先引入下面一个有用的引理.

|Dkw(x)|→0(|x|→∞), ∀k∈N, 0≤k≤m,

证明根据定理3，只需证明(34)式成立即可.

方程(9)两端同乘以2u，并在R上积分可得

(35)

其中，(·，·)表示L2(R)中的内积.

利用引理5和中值定理有

(36)

(h(ux)x,u)=-(h′(θ1ux)ux,ux)≤0,

(37)

(g(u)xx,u)=-(g′(u)ux,ux)≤0,

(38)

(G(u),u)=(G′(θ2u)u,u)≤γ0‖u‖2,

(39)

其中，0<θ1,θ2<1.将(36)～(39)式代入(35)式后，对t积分可得

3 Cauchy问题(9)，(10)解的衰减性质

定理5设以下条件成立：

②G∈C1(R),G(0)=0且存在常数γ0>0，使得∀z∈R成立G′(z)≤-γ0;

③1h∈C1(R),∀z∈R,h(z)z≥0;

③2h∈C1(R)，h(0)=0,存在常数α0>0,使得∀z∈R成立h′(z)≥α0;

④g∈C2(R),存在常数β0>0,使得∀z∈R成立g′(z)≥β0.

如果条件①，②，③1和④成立，min(γ0,1+β0)=σ0，则Cauchy 问题(9)，(10)的整体强解u∈C([0,∞);Hs(R))∩C1([0,∞);Hs-2(R))(s≥4)和整体古典解u(x,t)有衰减性质

‖u‖2+‖ux‖2≤(‖u0‖2+‖u0x‖2)e-2σ0t,t≥0.

(40)

如果条件①，②，③2和④成立，min(γ0,1+α0+β0)=σ，则Cauchy问题(9)，(10)的整体强解u∈C([0,∞);Hs(R))∩C1([0,∞);Hs-2(R))(s≥4)和整体古典解u(x,t)有衰减性质

‖u‖2+‖ux‖2≤(‖u0‖2+‖u0x‖2)e-2σt,t≥0.

(41)

证明利用引理5和对x进行分部积分，如果对于任意的z∈R,h(z)z≥0,得

(h(ux)x,u)=-(h(ux),ux)≤0;

(42)

如果h′(z)≥α0,利用中值定理有

(h(ux)x,u)=-(h(ux)-h(0),ux)=-(h′(θ3ux)ux,ux)≤-α0‖ux‖2,

(43)

其中，0<θ3<1;又有

(g(u)xx,u)=-(g′(ux)ux,ux)≤-β0‖ux‖2.

(44)

和

(G(u),u)=(G′(θ4u)u,u)≤-γ0‖u‖2,

(45)

其中，0<θ4<1.

将(36)，(42)，(44)和(45)式代入(35)式，得

(46)

解不等式(46)，推知(40)式成立.

将(36)，(43)～(45)式代入(35)式,有

(47)

解不等式(47)，推知(41)式成立.定理5得证.

致谢此文在郑州大学数学系陈国旺教授的指导下完成，特此感谢！

参考文献：

[1] Zhao Huijiang.Optimal temporal decay estimates for the solution to the multidimensional generalized BBM-Burgers equations with dissipative term[J].Applicable Analysis,2000,75(1/2):85-105.

[2] Zhao Huijiang,Xuan Benjin.Existence and convergence of solutions for the generalized BBM-Burgers equations with dissipative term[J].Nonlinear Analysis:Theory,Methods & Applications,1997,28(11):1835-1849.

[3] Zhao Huijiang.Existence and convergence of solutions for the generalized BBM-Burgers equations with dissipative term Ⅱ:the multidimensional case[J].Applicable Analysis,2000,75(1/2):107-135.

[4] Wang Shubin,Chen Guowang.Small amplitude solutions of the generalized IMBq equation[J].J Math Anal Appl,2002,274(2):846-866.

[5] Wang Shubin,Chen Guowang.Cauchy problem of the generalized double dispersion equation[J].Nonlinear Analysis:Theory,Methods & Applications,2006,64(1):159-173.

[6] Sogge C D.Lectures on Nonlinear Wave Equations[M].Boston:International Press of Boston,1995:6-9.

[7] 陈国旺，吕胜关.人口问题中广义三维Ginzburg-Landau模型方程的初边值问题[J].应用数学学报，2000，23(4)：507-517.

[8] 王耀东.偏微分方程的L2理论[M].北京：北京大学出版社，1989:42-44.