非光滑广义Dini-凸多目标规划解的充分性与对偶性

康瑞瑞， 张庆祥， 姜艳， 张文静

(1.北京交通大学 理学院 北京100044; 2.延安大学 数学与计算科学学院 陕西 延安 716000)

0 引言

众所周知,凸性和广义凸性在数学规划的很多方面都起着重要的作用,特别是在最优性充分条件和对偶理论方面更是如此.这主要是因为凸函数在非线性规划中有一些很好的性质，比如凸函数在凸集上的局部极小值一定是全局极小值.因此各种广义凸性的探索一直是凸分析的重要课题[1-10].Ben-Tal引入了广义加法、数乘和内积运算,Avriel在[3]中结合这些广义运算给出了一类非常重要的广义凸函数,即(h,φ)凸函数的概念.Ben-Tal[4]又进一步讨论了(h,φ)凸函数的一些基本性质.张庆祥[5-6]推广了这些广义凸函数，提出了若干类广义(h,φ)-凸函数的概念.另外，刘三阳[7]从Dini右上方向导数的角度,定义了几类广义不变凸函数,并研究了非光滑非凸规划解的充分条件.后来黄建明等[8]在张玉忠[9]的(h,φ)-Lipschitz基础上提出了弱(h,φ)-Lipschitz条件的概念.

基于以上研究，作者利用Ben-Tal广义代数运算,研究了非光滑广义Dini-凸多目标规划解的充分性与对偶性.

1 预备知识

先引进Ben-Tal广义代数运算，文中记Rn为n维欧氏空间，R为全体实数.h为定义在H⊆Rn上的n维实值向量连续函数,它具有反函数h-1,φ是定义在Φ⊆R上的连续实值函数,它具有定义在R上的单值反函数φ-1.

1)对于x，y∈H,定义h-向量加法为

x⊕y=h-1(h(x)+h(y));

2)对于x∈H和λ∈R,定义h-数乘为

λ⊗x=h-1[λh(x)]；

3)对α，β∈Φ的φ-加法定义为

α[+]β=φ-1(φ(α)+φ(β));

4)对于数α∈Φ和λ∈R,φ-数乘定义为

λ[·]α=φ-1(λφ(α));

5)对于x,y∈H的内积定义为

(xTy)h,φ=φ-1(h(x)Th(y))(假定右边有意义)；

6)h-向量减法和φ-减法分别表述为

xΘy=x⊕((-1)⊗y)=h-1(h(x)-h(y)),x，y∈H；

α[-]β=α[+]((-1)[·]β)=φ-1(φ(α)-φ(β)),α,β∈Φ.

记

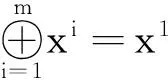
Rk为全体k维实体向量集

对于Ben-Tal广义代数运算,可以得到下面两个引理.

引理1若φ是Φ上的严格递增函数,则

1)若λ≥0,λ,α,β∈Φ且α≥β,则λ[·]α≥λ[·]β；

2)若λ>0,λ,α,β∈Φ且α>β,则λ[·]α>λ[·]β；

5)若φ是R上的严格单调一对一函数,且φ(0)=0,α,β∈R,则α<β当且仅当α[-]β<0.

引理2[10]1)若λ，α，β∈R,则λ[·](α[-]β)=λ[·]α[-]λ[·]β;

3)令若φ是R上的严格单调函数,λ<0,λ，α，β∈R且α≤β,则λ[·]α≥λ[·]β.

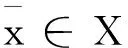
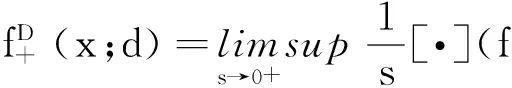
上述极限可以为无穷，因此广义Dini右上方向导数总是存在的.f在x处的广义Dini-梯度定义为

特别地，当φfh-1可微时，*f(x)=h-1(φfh-1(t)|t=h(x)).

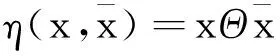
证明设f:C→R在C上是广义Dini不变凸的,则由定义4, 对∀x∈C,有

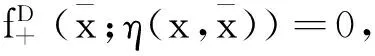
故f在C上是广义Dini不变凸的.

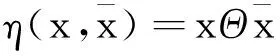
2 最优性充分条件

考虑下列多目标规划

记(VP)的可行集为

X={x∈Rn|gj(x)≤0,j=1,2,…,m;rk(x)=0,k=1,2,…,l}，

以下总假设:φ是严格递增函数,h-1(0)=0,φ(0)=0.

定义8设x*∈X,如果对任意的x∈X,均有

fi(x*)≤fi(x),

即对一切i=1,2,…,p,均有fi(x*)≤fi(x),则称x*是(VP)的绝对最优解.

定义9设x*∈X,如果不存在x∈X,使得

fi(x*)≥fi(x),(fi(x*)>fi(x)),i=1,2,…,p，

则称x*是(VP)的有效解(弱有效解).

(1)

(2)

(3)

结合(3)式得

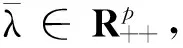
(4)

另一方面，对∀x∈X,有

(5)

(6)

(7)

(8)

(9)

(10)

再由引理1中的3),得

(11)

由(4),(11)和引理1中的4),得

(12)

证明对∀x∈X,有

(13)

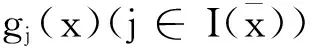
(14)

又因为对∀x∈X,总有

(15)

联合(14)与(15),对∀x∈X,得

(16)

由(1),引理2和引理1中的3),得

(17)

证明证明与定理3的证明类似.

(18)

(19)

证明定理4,5和推论2的证明依次与定理2,3和推论1的证明类似.

3 对偶性

下面考虑多目标规划(VP)的Mond-Weir型对偶问题

将上述式子两端相加,并由引理1中的3),得

(20)

(21)

参考文献：

[1] Clarke F H.Optimization Conditions and Nonsmooth Analysis[M]. New York: Wiley-Interscience, 1983： 20-116.

[2] Hanson M A.On sufficiency of the Kuhn-Tucker conditions[J]. J Math Anal & Appl, 1981, 80: 545-550.

[3] Avriel M.Nonlinear Programming: Analysis and Method[M]. New Jersey:Printice-Hall, 1976：50-389.

[4] Ben-Tal A. On generalized means and generalized convex functions[J]. J Optim Theory Appl, 1977, 21: 1-13.

[5] 张庆祥.一类(h,φ)-意义下半无限规划的最优性充分条件[J]. 系统科学与数学, 1991, 11(4): 367-370.

[6] 张庆祥.非光滑(h,φ)-半无限规划解的充分性和对偶性[J]. 应用数学学报, 2001, 24(1): 129-138.

[7] 刘三阳.非光滑非凸规划解的充分条件[J]. 应用数学学报, 1991, 4(1): 58-63 .

[8] 黄建明,云莲英. (h,φ)-方向导数与(h,φ)-次梯度[J].丽水学院学报, 2008, 30(2):13-17.

[9] 张玉忠. 弱Lipschtiz函数,它的广义次梯度及其在最优化中的应用[J].数学进展, 1992, 21(4): 439-444.

[10] 徐义红，刘三阳.(h,φ)-不变广义凸函数的若干性质与(h,φ)-不变广义凸多目标规划的最优性及对偶性[J].应用数学学报，2003，26(4)：726-736.