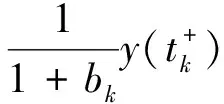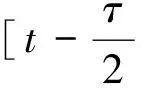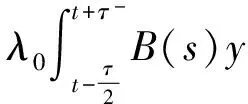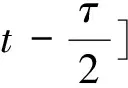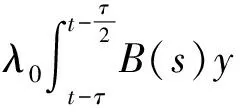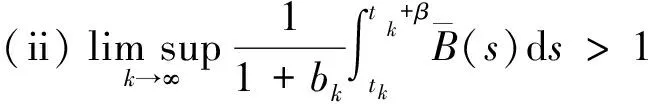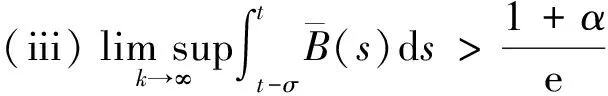具脉冲和时滞影响的向量抛物型方程振动性的新准则*

罗李平，王艳群，宫兆刚

(衡阳师范学院数学与计算科学系，湖南 衡阳 421002)

H-振动的概念是研究向量微分方程的新的有力工具，文献[1]在研究向量常微分方程时首次引入了H-振动的概念，这里H是Rm中的单位向量。关于这一概念及其应用，文献[2]作了很好的阐述。近年来，关于具时滞影响的向量偏微分方程的H-振动性研究已经取得了一些很好的结果[3-5]，但关于具脉冲和时滞影响的向量偏微分方程的H-振动性研究还相对较少[6-9]。本文的目的是讨论一类具脉冲和时滞影响的向量抛物型偏微分方程，利用H-振动的概念及内积降维的方法，将多维振动问题化为一维脉冲微分不等式不存在最终正解的问题，获得了这类方程在Dirichlet边值条件下所有解H-振动的若干充分条件。

考虑如下的基于脉冲和时滞影响的向量抛物型偏微分方程

(1)

同时考虑Dirichlet边值条件：

U(t,x)=0, (t,x)∈R+×∂Ω,t≠tk

(2)

其中0是Rm中的零向量。

在本文中，我们总假设下列条件成立：

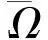
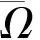
定义1 向量函数U(t,x)∈C2([t0,∞)×Ω,Rm)称为边值问题(1)-(2)的解，若U(t,x)满足：

(A)对固定的t,t≠tk,k=1,2,…,U(t,x)关于x二次可微；对t≠tk,k=1,2,…,x∈Ω,U(t,x)关于t一次可微，且满足方程(1)；

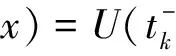
(C)对t≠tk,k=1,2,…,x∈∂Ω,U(t,x)满足边值条件(2)。

定义2 边值问题(1)-(2)的解U(t,x)称为H-振动的，若对Rm中的单位向量H及任意大的T≥0，存在一点(t0,x0)∈[T,∞)×Ω，使得内积=0。

众所周知[10]，Dirichlet特征值问题

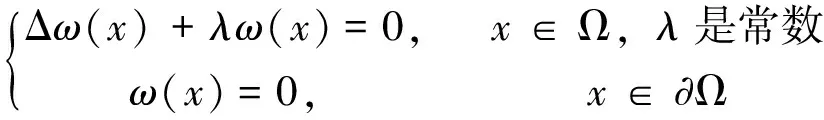
(3)

的第一特征值λ0>0，并且与λ0对应的特征函数φ(x)>0,x∈Ω。

为叙述方便，在本文中引入如下记号

UH(t,x)=，

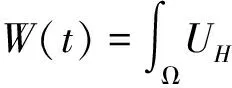
其中H是Rm中的单位向量，表示Rm中向量U和V的内积。

引理1 设H是Rm中的单位向量且U(t,x)是方程(1)的解。若UH(t,x)最终为正，则UH(t,x)是纯量脉冲抛物型偏微分不等式

(4)

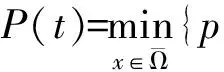
引理1的证明很简单，在此略去。

相应于边值条件(2)，考虑纯量边值条件：

UH(t,x)=0, (t,x)∈R+×∂Ω,t≠tk

(2′)

利用引理1，容易得到

定理1 设H是Rm中的单位向量。若在边值条件(2′)下纯量脉冲抛物型偏微分不等式(4)无最终正解，则边值问题(1)-(2)的所有解U(t,x)在G内H-振动。

定理2 设H是Rm中的单位向量。若脉冲微分不等式

(5)

无最终正解，则边值问题(1)-(2)的所有解U(t,x)在G内H-振动，其中λ0由问题(3)确定。

定理2的证明完全类似于文献[7]中的定理2，在此略去。

下面我们在上述讨论的基础上，给出判别边值问题(1)-(2)的所有解H-振动的进一步结果。

定理3 设H是Rm中的单位向量。若

(i)存在一常数β>0，使得tk+1-tk≥β,k=1,2,…，且τ≥β；

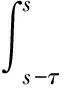
证明由定理2知，只需要证明在定理3的条件下，脉冲微分不等式(5)无最终正解即可。

假设脉冲微分不等式(5)存在最终正解W(t)，t≥T+τ>0,T≥0。由(5)易知当t≥T+τ,t≠tk时，W(t)在区间(tk,tk+1),k=1,2,…上非增且有

W′(t)+[λ0a(t)+P(t)]W(t)+

λ0b(t)W(t-τ)≤0,t≥T+τ,t≠tk

(6)

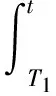
(7)

可得

y′(t)+λ0B(t)y(t-τ)≤0,t>T1+τ,t≠tk

(8)

由(7)-(8)两式可知，y(t)是一个非增函数。

对t=tk，结合(5)中的脉冲条件，有

λ0a(ξ)+P(ξ)]dξ)≤

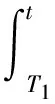
(1+bk)y(tk)

(9)

对(8)式从tk到tk+β积分，并注意到y(t)的非增性可得

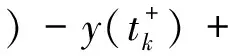
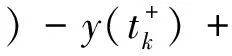
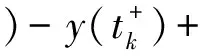
(10)

由(9)-(10)两式得

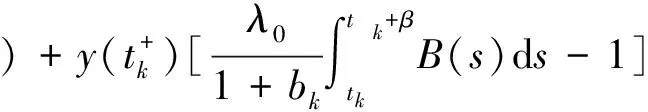
这与条件(ii)矛盾。证毕。

类似定理3的证明可得如下结论。

定理4 设H是Rm中的单位向量。若

(i)存在一常数β>0，使得tk+1-tk≥β,k=1,2,…，且β>τ；

则边值问题(1)-(2)的所有解U(t,x)在G内H-振动，其中λ0由问题(3)确定。

定理5 设H是Rm中的单位向量。若

(i)存在一常数β>0，使得tk+1-tk≥β,k=1,2,…，且β>τ；

(ii)存在某一常数α>0，使得0

则边值问题(1)-(2)的所有解U(t,x)在G内H-振动，其中λ0由问题(3)确定。

证明由定理2知，只需要证明在定理5的条件下，脉冲微分不等式(5)无最终正解即可。

假设脉冲微分不等式(5)存在最终正解W(t)，t≥T+τ>0,T≥0。则类似于定理3的证明可知，

则有

≥≥

(s-τ)ds≤0

于是有

≥(s-τ)ds≥

(11)

τ(s-τ)ds≤0

则有

(12)

于是，由(11)-(12)两式有

从而有

≤≤M

因此，V(t)有上界。

对充分大的t，由(8)式可得

≤0

(13)

又由于

(14)

于是，由(13)-(14)两式可得

≥

(15)

因此

这与条件(iii)矛盾。证毕。

由脉冲微分不等式(5)有

W′(t)+[λ0a(t)+P(t)]W(t)+

Q(t)W(t-σ)≤0,t≥T+τ,t≠tk

类似定理3-定理5的证明可得如下结论。限于篇幅，其证明在此略去。

定理6 设H是Rm中的单位向量。若

(i)存在一常数β>0，使得tk+1-tk≥β,k=1,2,…，且σ≥β；

定理7 设H是Rm中的单位向量。若

(i)存在一常数β>0，使得tk+1-tk≥β,k=1,2,…，且β>σ；

则边值问题(1)-(2)的所有解U(t,x)在G内H-振动。

定理8 设H是Rm中的单位向量。若

(i)存在一常数β>0，使得tk+1-tk≥β,k=1,2,…，且β>σ；

(ii)存在某一常数α>0，使得0

则边值问题(1)-(2)的所有解U(t,x)在G内H-振动。

参考文献：

[1]DOMSLAK JU I.On the oscillation of solutions of vector differential equations [J].Soviet Math Dokl,1970,11: 839-841.

[2]COURANT R,HILBERT D.Methods of Mathematical Physics,Volume I [M].New York: Interscience,1996.

[3]MINCHEV E,YOSHIDA N.Oscillation of solutions of vector differential equations of parabolic type with functional arguments [J].J Comput Appl Math,2003,151(1): 107-117.

[4]LI W N,HAN M A,MENG F W.H-oscillation of solutions of certain vector hyperbolic differential equations with deviating arguments [J].Appl Math Comput,2004,158(3): 637-653.

[5]LUO L P.Oscillation of solutions of neutral vector parabolic equations with continuous distribution delay[C]∥Proceedings of the 7th Conference on Biological Dynamic System and Stability of Differential Equation,Vol.Ⅱ,Liverpool: World Academic Press,2010:664-668.

[6]LI W N,HAN M A.Oscillation of solutions for certain impulsive vector parabolic differential equations with delays [J].J Math Anal Appl,2007,326(1): 363-371.

[7]罗李平,俞元洪.脉冲向量中立型抛物偏微分方程的H-振动性[J].数学学报,2010,53(2): 257-262.

[8]罗李平,杨柳,曾云辉.脉冲向量中立型抛物方程解的H-振动性[J].高校应用数学学报:A辑,2010,25(4): 463-468.

[9]罗李平,俞元洪.脉冲向量时滞双曲型方程的H-振动性[J].中山大学学报：自然科学版,2008,47(6): 1-4.

[10]GILBARG D,TRUDINGER N S.Elliptic partial equations of second order [M].Berlin: Springer-Verlag,1977.