面向随机振动功率谱估计的小波变换去噪算法理论分析*
罗中良,汪华斌,陈治明,杨发权
(1.惠州学院电子科学系,广东 惠州 5160072.佛山科学技术学院电子与信息工程学院,广东 佛山 528000)
振动试验的目的在于确定所设计的设备在运输、工作过程中能承受外来或者自身产生的振动而不被破坏,能正常发挥性能,并达到预定的使用寿命。振动大约占整个环境因素的27%,可见振动试验在环境试验中的重要地位[1-3]。在可靠性振动试验中,随机振动谱均衡控制中首先是通过对功率谱的估计,再利用均衡控制算法与参考谱进行比较迭代,最终使控制谱收敛到参考谱。实验证明谱估计的误差会引起自调整算法误差显著增大甚至不能收敛[4]。传统基于FFT 的周期图法对功率谱作估计由于缺少对估计值的统计平均,因此产生方差大[4-10],韦斯(Welch)法,可以减小谱估计的误差,却降低了谱估计的频率分辨率[11]。增大处理数据量提高频率分辨率的同时造成系统回路时间变大,影响到系统的均衡性能。小波变换是一种时间-尺度分析方法,具有多分辨分析的特点,且具有时频两域表征信号局部特征的能力[6.9],很适合于振动频谱均衡控制,如B.Williams[12]、LIU的研究[4]。
在通过对小波系数进行阈值处理去除低幅度噪声时,由于振动谱对数域中噪声统计模型在各频率点是相关的,这为小波去噪方法直接应用振动功率谱估计提出了难题。另外,振动功率谱通常存突变和间断现象,在采用软阈值方法时得到的估计信号在间断处会显得比较模糊,且整体误差较大。而硬阈值方法在间断点附近会产生伪Gibbs现象。实际上,软、硬阈值方法在去噪和保护间断方面处于两个极端,若适当将这两种方法折衷,则能够取得更好的去噪效果,从而提高谱均衡的整体性能。为此,本文通过对随机振动谱的统计模型进行分析,推导出非线性阈值与小波变换尺度之间的关系,为滤波去噪提供依据,也为自适应阈值算法提供理论支撑。
1 面向振动谱估计的小波变换去噪阈值理论分析
1.1 谱估计统计特征及其噪声模型
对于零均值的平稳高斯过程{x(t),t:0,1,...,2N-1},加w(t)窗的傅里叶变换为:
(1)
(2)
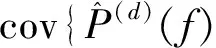
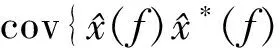
(3)
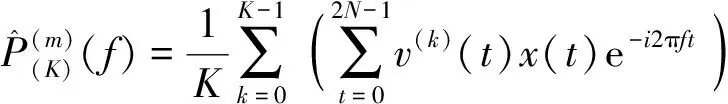
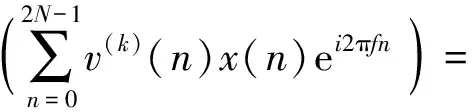
(4)
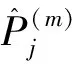
,
(5)
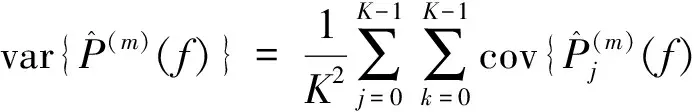
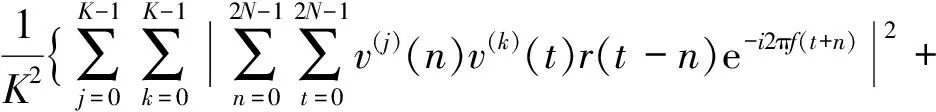
(6)
若信号序列{x(t),t:0,1,...,2N-1}是零均值的高斯白噪声,方差为σ2,则式(5)可写为:
,
(7)
对于高斯白噪声或非高斯的平稳随机过程,MTSA估计器的统计分布为:
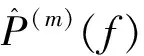
(8)
(9)
1.2 对数功率谱模型
1.2.1 周期图谱估计器的对数功率谱模型 对周期图估计器进行对数变换,将功率谱估计值变换到对数坐标,即:
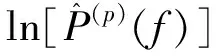
(10)
对应的的期望与方差为:
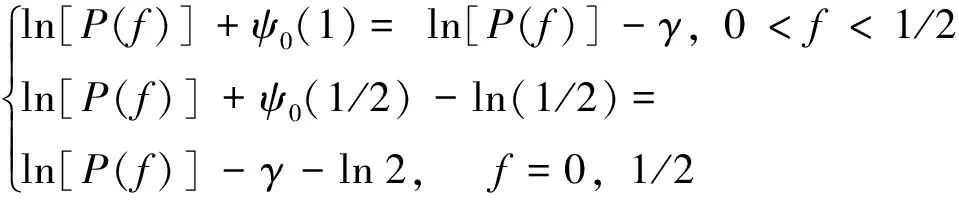
(11)
(12)
其中,ψ0(·)是Digamma函数;ψ1(·)是Trigamma函数;γ是Euler-Mascheroni常数,其值约为0.577 216。式(12)表明经对数变换的PSD,其方差不再依赖PSD的真值,而是一常量。
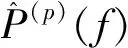
,≤f≤1/2
(13)
其中,{u(f),0 (14) γ=lnP(f)+ε(f), 0≤f≤1/2 (15) (16) 由此可见,对数周期图谱估计(与常数γ之和)等于真实的对数PSD与零均值、方差为π2/6的非高斯随机变量之和,因将对数功率谱密度中的噪声项ε(f)滤除可以提高谱估计的精度,减小谱估计的方差。 1.2.2 MTSA谱估计器对数功率谱模型 对式(8)进行对数变换得: (17) 对应的期望与方差为: (18) (19) 类似于1.2.1节分析式(15)结果,可得: ψ0(K)+lnK=lnP(f)+η(f), 0≤f≤1/2 (20) (21) 当对式(20)以傅里叶频率进行离散频率采样时,可知η(f)的傅里叶r频率点的值是相关的。为了后面描述方便,现定义: sη(ω)≡cov{η(f),η(f+ω)}= cov{ln[W(f)],ln[W(f+ω)]} (22) sη(ω)= (23) 由于实际中MTSA谱估计器较周期图谱估计器应该广泛的多,因此,仅讨论MTSA谱估计器噪声小波变换系数的方差与小波变换尺度的关系,从而为非线性阈值处理提供理论依据。为了表述上方便,记(20)式记为: ≡ψ0(K)+lnK= (24) 对上中的f以傅里叶频率进行离散采样,得到 (25) 其中离散傅里叶频率fk=k/2N。 对式(25)进行尺度为J的小波变换 (26) 以下分析如何采用阈值法将噪声序列的小波变换系数滤除,从而得到对数功率谱lnP(fk)的估计。 由式(23)可以得到η(fk)各频率间的协方差阵(自相关矩阵)为 (27) (28) 在式(26)中,设gT为WJ中产生Εj,t的行向量,即Εj,t=bTη,由于WJ是实矩阵,有gH=gT,因此Εj,t的方差可表示为: var{Εj,t}=gTRηg=[FTg]HDFTg (29) (30) 由于在同一尺度下,gT是由序列的移位而产生的,其傅里叶变换的模相等,因此: (31) 上式说明噪声η的小波系数的方差仅与小波变换的尺度有关,而与时移参数无关,可得到与小波变换尺度相关的非线性阈值处理,其尺度为j时的阈值为 (32) 根据以上分析,基于小波变换的MTSA谱估计非线性(自适应)阈值算法具体步骤为: 1){x(t),t:0,1,...,2N-1}为一平稳随机过程的2N点采样序列,通过预处理使其均值为零; 2)选择合适的K值,计算多窗口序列; 5)依据式(23)、(27)、(31)和(32)分别计算尺度j上的噪声η的小波系数的方差及对应的阈值; 6)选择合适的小波系数非线性处理方法,如硬阈值处理法、软阈值处理法或中值法对小波系数进行非线性处理; 7)通过小波逆变换,得到对数功率谱lnP(fk)的估计。 为了检验上述算法的性能,选用周期图功率谱估计和N=1 024、K=4的多正弦窗口序列MTSA法功率谱估计以及本文算法进行比较。在本文算法仿真时使用Coiflet小波,并采用文中推导的阈值在对数功率谱估计时进行非线性去噪。三种算法对随机振动功率谱估计性能的比较如图1所示,图1(a)为经滤波、抽样后的2 048点随机振动时域信号,抽样后的采样频率为8.192 kHz。从图1(b)、(c)、(d)看出,周期图谱估的功率谱波动范围为21.9 dB,MTSA法得到的功率谱计法得波动范围为11.3 dB,而本文算法得到的功率谱波动范围降低为6.9 dB,并保持了振动谱的边缘陡峭度,表明了本文方法的有效性。 1)构建了小波域振动谱估计噪声统计模型及对应的对数域振动谱噪声的统计模型; 2)在噪声模型基础上,理论推导了噪声小波系数方差与尺度关系,并得到阈值与尺度的数值关系; 3)构建了通用的小波自适应去噪谱估计方法,在抑制谱振荡和保护谱突变之间取得平衡; 4)通过仿真对研究成果进行了验证,证明算法的有效性。 参考文献: [1]侯瑞,陈国平.振动台虚拟试验的建模和仿真研究[J].力学季刊,2008,29(2):254-258. [2]关广丰,丛大成,韩俊伟.随机振动功率谱复现迭代算法的研究[J].地震工程与工程振动,2006,26(6):71-76. [3]宦海祥.电动振动设备的发展及展望[J].环境试验,2006,28(4):28-31,2006. [4]LIU Xiaoyong,YAO Xianghua,SHI Ren.Research on improving the performance of random vibration spectrum equalization using wavelet analysis[J].Mini-Micro Systemss,2004,25(12):2273-2276. [5]LIU Xiaoyong,LUO Zhongliang,YI Mingzhu.New frequency-domain method for shock vibration control[J].中山大学学报:自然科学版,2008,47(5):49-53. [6]周有平,罗中良.基于振动工程相位检测的故障诊断方法研究[J].中山大学学报:自然科学版,2009,48(2):45-50. [7]CRISTAN A C,WALDEN A T.Multitaper power spectrum estimation and thresholding: wavelet packets versus wavelets[J].IEEE Transactions on Signal Processing,2005,50:2976-2986. [8]罗中良,李昕.基于小波变换的红外弱小目标检测新方法[J].红外技术,2006,28(8):456-559. [9]张峰,石现峰.多正弦窗谱估计应用于振动信号频谱分析[J].西安工业大学学报,2010,30(4):387-391. [10]余训锋,马大玮,魏琳.改进周期图法功率谱估计中的窗函数仿真分析[J].计算机仿真,2008,3,25(3):111-114. [11]吴红卫,吴镇扬,赵鹤鸣.多正弦窗谱估计的性能分析[J].信号处理,2007,23(6):932-936. [12]KARSHENAS A,DUNNIGAN M,WILLIAMS B.Wavelet power spectrum smoothing for random vibration control[J].IEEE Transactions on Industrial Electronics,1999,46:466-467.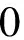
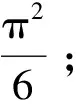
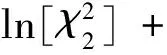
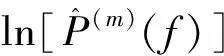
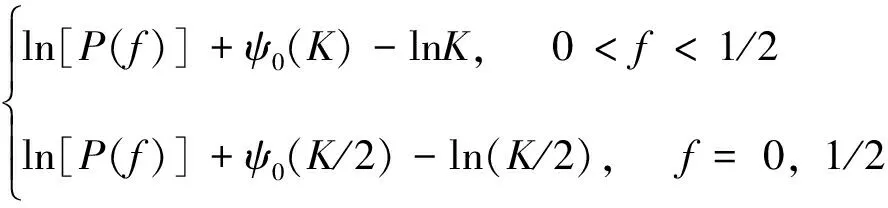
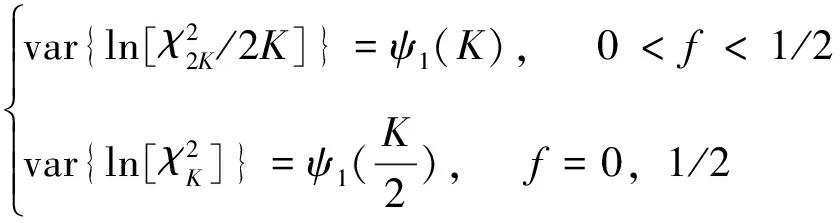
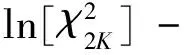
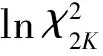
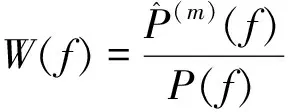
1.3 噪声小波变换系数的方差与小波变换尺度的关系
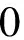
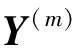
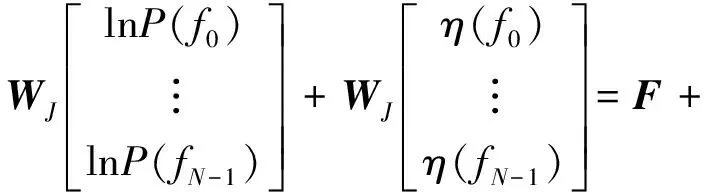
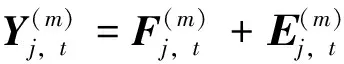
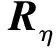
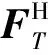
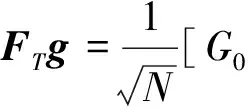
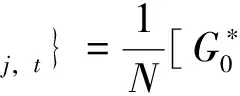
2 面向振动谱的小波变换自适应噪声消除快速算法及仿真
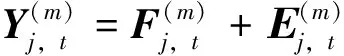
3 结 论

