基于最大熵谱估计的某型飞行模拟器动态性能验证
王哲,李国辉,赵善禄
(空军航空大学军事仿真研究所,长春130022)
0 引言
经典谱估计虽然计算效率高,但是由于窗函数的局限性,在计算过程中不可避免地出现频谱泄露、谱峰转移、分辨率低等缺点。针对经典谱估计的局限,现代谱估计方法应运而生,其中最大熵谱估计法是一种常用的现代谱估计方法。
1 最大熵谱估计与一致性验证
1.1 最大熵谱估计
1967年,Burg最早将“熵”这一概念从信息论中引入到谱估计中,提出最大熵谱估计[1]。最大熵谱估计具有分辨率高,使用范围广的特点。
“熵”是对于随机性进行度量的量,熵值越大,则随机性越大。假设p(x)为连续随机变量的概率函数密度,则“熵”可以定义为:
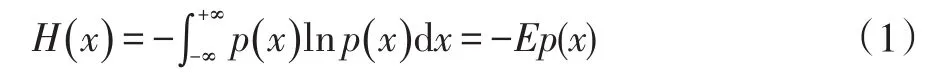
如果平稳时间序列{xt,t∈Z}是正态随即过程,其功率谱为S(ω),那么功率谱熵为:
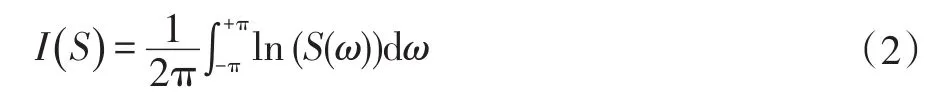
与熵的原始定义相似,I(S)表示随即序列不确定性的度量,I(S)值越大,表明随机性越强。根据谱估计知识可知,样本序列自相关函数和功率谱密度构成傅里叶变换对,在已知相关函数r(m),m=0,1,2,…,p情况下,对m>p的自相关函数进行外推,当功率谱S(ω)满足如下约束条件:

当在上数条件下使得H(S(ω))最大时,这样的过程称为最大熵谱估计,估计出的Ŝ()ω为最大熵谱。可以证明,正态随机过程的最大熵谱估计与AR模型谱估计是等效的[2]。AR模型的功率谱为:要想求信号功率谱密度pn(ω),需要求出上式中的参数φ和σ。可以通过Yule-Walker法或Burg法求得相关参数,具体过程见参考文献[3]。当确定相关参数后,就可通过4式计算功率谱。
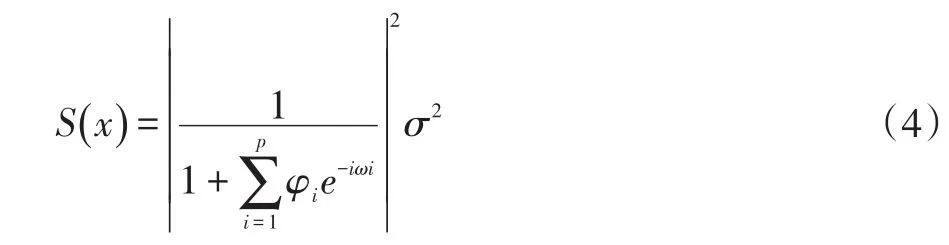
1.2 一致性验证
对最大熵谱估计进行一致性检验,有常规的非参数检验、窗谱估计一致性检验和最大熵谱估计一致性检验等多种方法[4]。本文采用最大熵谱估计一致性检验法与模型相结合进行检验。
最大熵谱估计的统计结果是有限的近似结果,是渐进无偏与渐进正态的[5]。当采样数目N与AR模型的阶数M足够大时,最大熵谱的均值与方差为:
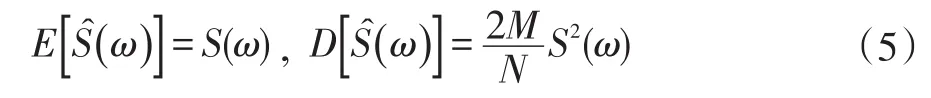
对 Ŝ(ω )作对数变换得到logŜ(ω ),由于 Ŝ(ω)是正态的,所以 logŜ(ω )仍为正态的。logŜ(ω)的均值和方差为:
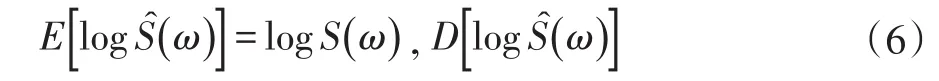
该对数谱 logŜ(ω)的100(1 -α)%置信区间近似为
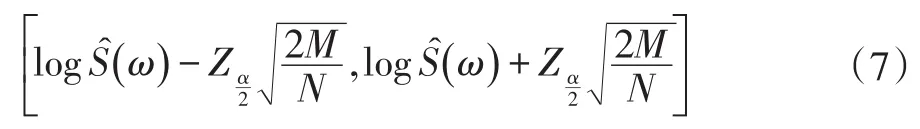
对于两个独立时间序列的功率谱密度均渐进正态情况下,第i个带宽中对数的抽样分布近似为:
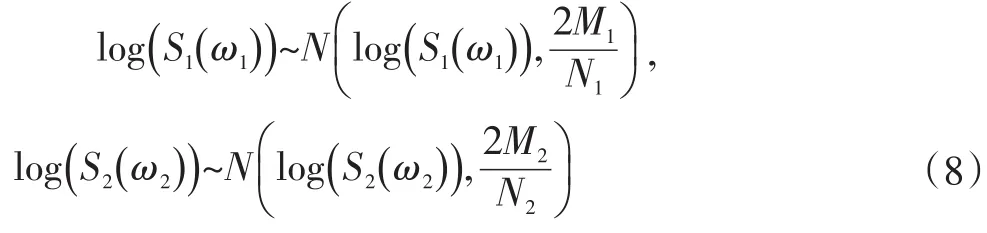
假设两个时间序列具有相同功率谱密度函数,即S1(ω1)=S2(ω2),根据式8可以得出:
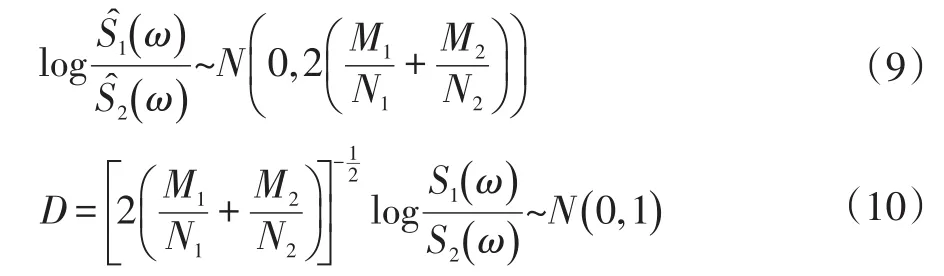
该假设检验的接受域是[ ]-Zα/2≤D≤Zα/2,α 为该检验的显著水平,N1、N2是两次试验的样本容量,M1、M2是AR模型的阶次。
在检验过程中,原则上对每个频率点都要进行检验,如果每个频率点都接受该检验,则说明两序列相容。检验的公式为:
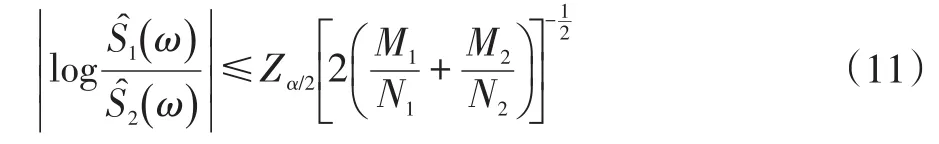
但是,与窗谱估计一致性检验类似,在实际验证过程中,由于频率点过多并且有的点功率谱较弱,所以工程中常常关注于频率谱较强的点。
2 实例验证
由前面章节的知识可知,对于正态随机过程,可以通过建立与之等效的AR模型进行最大熵谱估计。本节仍采用飞机水平加速的纵向过载nx随飞行速度ViV变化的仿真数据与试飞数据进行一致性检验。故需先建立AR模型。
在对仿真数据与试飞数据进行最大熵谱估计前,首先需要建立AR模型。由于经过数据预处理,仿真数据与试飞数据均可视为正态随机过程,可以参考文献[6]中时序建模的方法建立AR模型。对于模型阶数的确定,目前有多种准则与方法,主要有赤池FPE准则、AIC准则和Parzen的自回归传递函数准则[7]。本文对于模型阶数的确定,采用工程上常用的经验公式由于采样数目为N1,N2=3000,则M≈18,采样频率为
阶数为 P,模型参数为 φ1,φ2,…,φP的 AR(p)可以表示为
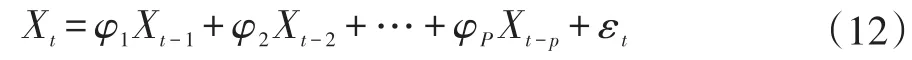
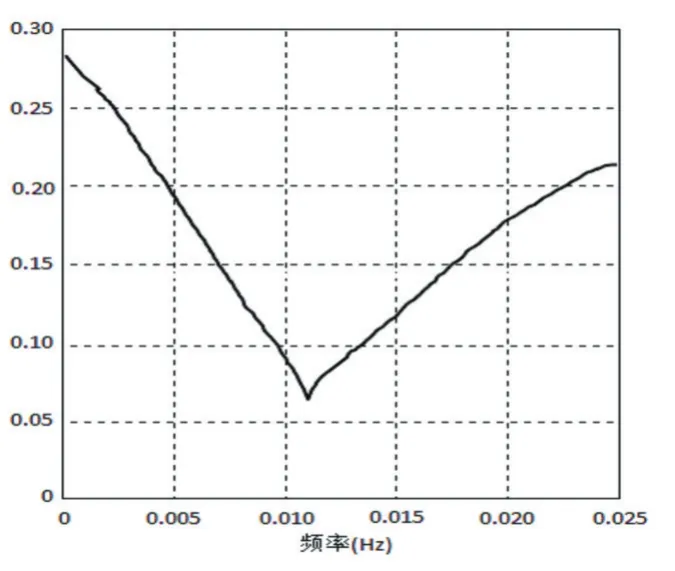
其中,{εt}是白噪声序列,满足 EXsεt=0 对一切s 采用Marple算法解yule-walker方程,利用MATLAB软件计算出相关参数,得到仿真数据的AR模型为: Xt=1.5761Xt-1-0.7562Xt-2-0.5123Xt-3-0.3165Xt-4+0.2119Xt-5+0.0352Xt-6-0.0158Xt-7-0.0264Xt-8+0.0322Xt-9+0.0286Xt-10-0.0346Xt-11+0.0153Xt-12-0.0234Xt-13+0.0315Xt-14+0.0446Xt-15-0.0061Xt-16+0.0019Xt-17+0.0211Xt-18 试飞数据的AR模型为: Xt=1.3213Xt-1-0.8613Xt-2-0.7449Xt-3-0.4881Xt-4-0.3591Xt-5-0.1011Xt-6-0.0695Xt-7+0.0987Xt-8+0.0413Xt-9-0.0363Xt-10-0.0303Xt-11-0.0134Xt-12+0.0006Xt-13+0.0201Xt-14+0.0362Xt-15-0.0061Xt-16+0.0109Xt-17+0.0211Xt-18 根据4式对仿真数据与试飞数据进行最大熵谱估计,得到如图1所示功率谱对比曲线。 图1nx随Vi变化最大熵谱估计对比曲线 根据归一化处理后的功率谱密度,确定主要频率区间为[0,0.025],因此可以对该区间内的频率点进行一致性检验。要验证nx随Vi变化的试飞数据功率谱S1(ω1)和仿真数据功率谱S2(ω2)的相容性,需要检验S1(ω1)=S2(ω2),构造统计量D: 其中,M1,M2为AR模型阶次,N1,N2为采样点数量,α为显著水平,统计量D对于该假设检验的接受域为[ ] -Zα/2,Zα/2,按公式 11进行检验: 当显著水平 α取 0.05时,查表得 Zα/2=1.96,N1=N2=3000,M1=M2=18,计算得B≈0.30。因此,只需要验证在主要频率区间内每个频率点处A的值小于0.30,就可以说明试飞数据与仿真数据的功率谱密度具有一致性。图2为A在[0,0.025]区间内的曲线图。 图2nx随Vi变化最大熵谱估计验证曲线 由图2可知,在主要频率区间内,有A≤B,所以在置信水平为95%情况下,S1(ω1)=S2(ω2)成立,即 nx随Vi变化的试飞数据与仿真数据具有一致性。 本文以飞机在某高度平飞加速过程中过载随速度的变化为例,采用最大熵谱估计法对仿真数据和试飞数据进行一致性检验,取谱峰附近[0,0.025dB]作为主要频率区间,检验结果显示,功率谱的主要频率点在95%的置信水平下,nx随Vi变化的仿真数据与试飞数据在统计意义下一致,该方法适用于其他动态飞行性能的一致性检验。 [1]李鹏波.时间序列样本的总体一致性检验——频域方法[J].飞行器测控学报,1999,18(4). [2]曾鸣,李雪青,谢保川,等.基于飞参数据的飞行仿真模型验证[J].指挥控制与仿真,2011,6(12). [3]徐慧娟.自回归AR模型的整体最小二乘分析研究[D].上海:东华理工大学,2012. [4]李鹤.基于试飞数据的模型飞行模拟器飞行性能验证研究[D].空军工程大学,2009. [5]李鹏波,高霞.应用最大熵谱估计进行导弹系统的仿真模型验证[J].国防科技大学学报,1999,21(2). [6]李鹤,吕岩,李国辉.飞行仿真动态数据验证的时序建模方法[J].兵工自动化,2008,27(12). [7]王建华,符文星,董敏周.最大墒谱估计在空空导弹仿真模型验证中的应用[J].弹箭与制导学报,2005,25(4).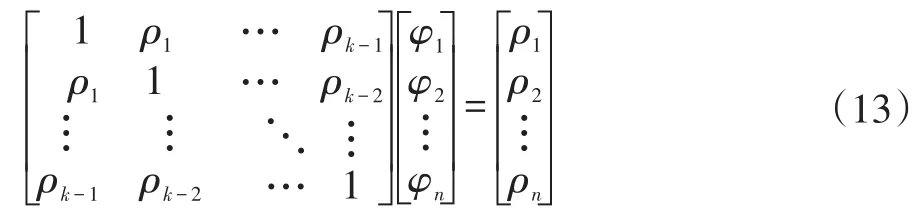

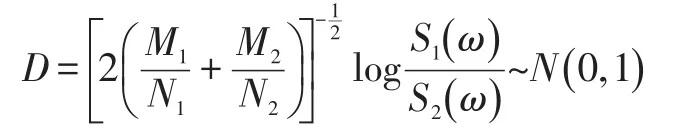
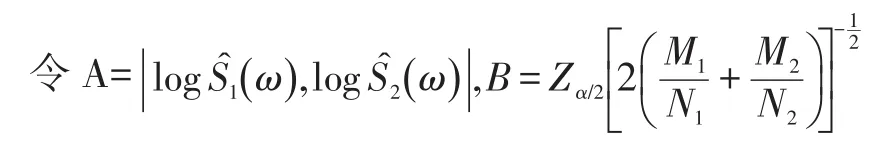
3 结语

