我国货币政策与通货膨胀的非线性机制识别
张小宇,刘金全
(吉林大学 数量经济研究中心,吉林 长春 130012)
一、引 言
利率作为货币政策的主要调控工具,其调整机理及作用效果一直受到货币当局及经济学家的高度关注。特别是利率与通货膨胀之间的作用机制更是人们关注的焦点。Fisher(1930)首次提出利率与通货膨胀的关系。Fisher将名义利率分解成两个部分,即实际利率和预期通货膨胀,并指出在完全预期的情况下,实际利率由经济中的实际因素决定,与预期通货膨胀无关。因此,预期通货膨胀只会一对一地影响名义利率。这就是著名的“费雪效应”。
随后人们开始检验费雪效应。起初,人们将滞后通货膨胀作为预期通货膨胀的代理变量,并采用分布滞后模型检验名义利率与通货膨胀的关系,尽管分布滞后模型估计方法不同,但检验结果是一致的,都证实费雪效应是成立的 (Gibson,1970;Lahiri,1976)。但将适应性预期作为通货膨胀的代理变量受到了人们的质疑。
Fama认为,如果市场是有效的,那么当前的利率水平能够反映未来的价格变化。因此,通货膨胀预期不仅包含过去的价格变化,还应包含对未来价格变化的预期。Fama(1975)在理性预期框架下分析了美国一月期债券利率与消费价格指数变化之间的关系。结果表明,过去债券利率的变化包含了未来消费价格指数变化的信息 (Fama,1975)。
Engle和Granger(1987)以及Johansen(1990)提出协整理论后,人们更加关注对名义利率与通货膨胀的长期均衡关系的检验。但检验结果存在很大差异,大部分研究表明美国利率与通货膨胀之间存在费雪效应(Bonham,1991;Jacques,1995)。然而,在其他经合组织国家,费雪效应似乎并不成立;在发展中国家,除了拉丁美洲国家明显存在费雪效应外,其他国家并没有得到一致的检验结果(Cooray,2002)。
我国学者刘金全等(2003)利用单位根及分整检验等方法检验名义利率和通货膨胀率序列的单位根性质,并利用协整检验判断二者之间的长期关系。检验结果表明,我国通货膨胀对名义利率的作用并不明显,我国经济当中没有出现显著的费雪效应。本文在名义利率与通货膨胀协整检验的基础上,构建TVECM模型,识别名义利率与通货膨胀的非线性及非对称调整特征。
二、名义利率与通货膨胀的费雪效应检验
目前检验费雪效应主要采用协整方法。如果名义利率与通货膨胀率存在长期协整关系,并且协整向量为(1,1),则认为存在费雪效应;如果二者存在长期协整关系,但协整向量不是(1,1),则二者存在“弱费雪效应”;否则,不存在费雪效应。
1.数据选取及平稳性检验
图1给出了1996年1月至2010年3月我国银行间同业拆借加权平均利率(以下简称拆借利率)与金融机构人民币一年期存款基准利率(以下简称存款利率)变化曲线①。从拆借利率与存款利率的变化路径可以看出,二者具有相同的变动趋势(序列的趋势成分采用H-P滤波方法获得)。与存款利率相比,拆借利率的波动更加灵敏,更能反映货币供需关系的变动,因此本文选择拆借利率作为名义利率的代理变量。通货膨胀率由消费价格指数计算得到。

图1 拆借利率与存款利率变化曲线

图2 残差序列
为检验名义利率与通货膨胀的协整关系,首先要检验名义利率与通货膨胀率序列的单位根性质。我们采用扩展的Dicky-Fuller(简称ADF)检验及Phillips-Perron(简称PP)检验对序列进行单位根检验。ADF检验模型的滞后阶数均根据SIC信息准则进行选取。检验结果见表1。

表1 名义利率与通货膨胀率序列的单位根检验
从单位根检验结果可以看出,名义利率和通货膨胀率序列的水平值均在1%的显著性水平上接受存在单位根的原假设,而相应的差分序列则拒绝存在单位根的原假设,说明名义利率与通货膨胀率序列均为一阶单整过程。进一步我们可以通过检验名义利率与通货膨胀率序列是否存在协整关系来检验费雪效应。
2.费雪效应检验
采用Engle-Granger两步法检验名义利率与通货膨胀率的协整关系②。第一步,用最小二乘法估计名义利率对通货膨胀率的线性方程,估计结果为 (括号中的数字为对应参数的t统计量):

第二步,提取上述回归模型的残差序列 (见图2),并进行单位根检验,如果残差序列是平稳的,说明名义利率与通货膨胀率存在协整关系。从残差图可以看出,残差序列带有明显的时间趋势,为一非平稳时间序列,ADF检验以及PP检验的结果证实了这一点 (检验结果略)。表明我国名义利率与通货膨胀率之间不存在长期的均衡关系,即不存在费雪效应③。
为了进一步研究名义利率与通货膨胀的关系,我们在模型(1)中添加时间趋势项,得到回归方程的结果为:

提取残差序列并进行单位根检验表明 (残差序列见图2),在1%的显著性水平下拒绝残差项存在单位根的原假设(检验结果略),表明名义利率、通货膨胀率与时间趋势项之间存在长期均衡关系,之所以出现这样的结果与本文所选样本区间内名义利率存在明显的下降趋势有关 (见图1)。
三、TVECM模型及名义利率与通货膨胀的非线性及非对称调整的识别
尽管我国名义利率与通货膨胀之间并不存在费雪效应,但名义利率、通货膨胀率与时间趋势项之间却存在长期均衡关系,因此我们可以在协整检验的基础上,构建误差修正模型识别名义利率的短期调整特征。但无论是Engle-Granger的误差修正模型还是Johansen基于VAR的误差修正模型都假设变量服从线性调整机制,并不能识别出变量的非线性调整特征。Balke和Fomby(1997)首次将非线性引入到协整模型中,建立了门限协整模型(threshold cointegration)。随后此模型得到了广泛的应用(Enders and Falk,1998;Baum,Barkoulas and Caglayan,2001;Enders and Siklos,2001;Caner and Hansen,2001)。Hansen (2002)构建TVECM(门限向量误差修正模型)模型用于识别变量向长期均衡调整的非线性及非对称特征。本文拟构造一个两区制TVECM模型识别名义利率与通货膨胀的非线性及非对称调整机制。
1.名义利率与通货膨胀的两区制TVECM模型
假设β为名义利率与通货膨胀的协整向量(包含时间趋势项和截距项),μt(β)为误差修正项,则TVECM模型可表示为:
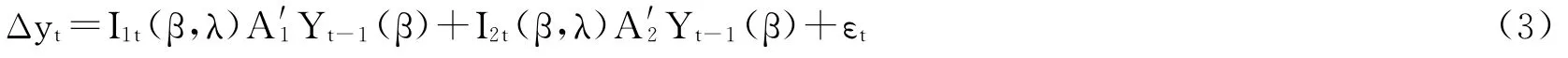
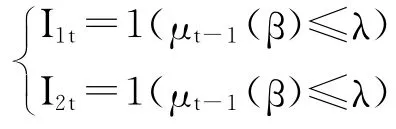
上述模型按照误差修正项分为两个区制,除了协整向量,其余参数在两个区制内均可取不同值。为了保证上述门限模型有意义,必须保证0<P(ut-1(β)≤λ)<1,否则模型不存在门限效应,另外为了保证有足够样本识别门限参数λ,通常假设:

其中,π1、π2称为调整参数 (trimming parameter)(Chan and Tong,1990;Chan,1993)。
2.协整向量β与门限值λ的参数估计
当εt服从高斯分布时,可利用极大似然法估计模型,对数似然函数为:

通常为了计算方便,首先固定参数β、λ,计算限制性对数极大似然函数 (相当于普通最小二乘回归),得到A1、A2、εt和Σ的估计值为:

进而得到“中心化”似然函数(concentrated likelihood function)为:

3.门限效应检验与非对称性的识别
当A1=A2时,模型 (3)为一线性误差修正模型。否则,为一非线性误差修正模型,表明模型存在门限效应。为了识别名义利率与通货膨胀的非对称调整机制,我们只需考查系数矩阵中对应的误差修正项系数在两个区制上是否相等,即是否等于其中分别为系数矩阵A1、A2的第三行向量。如果不相等,表明模型存在非对称调整特征。特别地,如果表明名义利率存在非对称调整特征表明通货膨胀存在非对称调整特征。可以构造 Wald统计量检验上述门限效应及非对称性 (Tsay,1989,1998)。由于在模型(3)中估计协整向量将导致门限效应的检验功效降低 (Hansen and Seo,2001)。因此模型(3)的协整向量直接采用Johasen的线性VAR模型估计。
4.名义利率与通货膨胀的TVECM模型估计结果
表2给出了不同滞后阶数模型估计的门限值、不同区制包含的样本个数比、对数似然函数以及相应门限效应检验的结果。

表2 名义利率与通货膨胀的TVECM模型门限效应检验结果
从表2的估计结果可以看出,1-6滞后阶数的模型均存在门限效应。其中,滞后阶数取1时,模型在5%的显著性水平上显著,其他模型均在1%的显著性水平上显著。另外,从门限值的估计结果可以看出,滞后阶数取3时的门限值估计结果与其他滞后阶数模型的估计结果有明显差别,基于此,再结合模型的对数似然值及AIC统计量,名义利率与通货膨胀的TVECM模型的滞后阶数取1,模型的估计结果为④:

四、主要结论及经济政策启示
通过对名义利率与通货膨胀的协整检验及名义利率与通货膨胀的非对称调整机制的识别,我们得到如下基本结论及经济政策启示:
首先,费雪效应假说在我国并不成立。由于名义利率与通货膨胀不存在协整关系,表明在本文检验的时间区间内名义利率与通货膨胀之间不存在长期均衡关系,进而说明费雪效应在我国并不成立。不存在费雪效应的主要原因与我国目前银行间拆借利率没有完全市场化以及利率政策缺乏有效的传导机制和反应机制有关。

图3 误差修正效应曲线
其次,我国名义利率存在非对称调整偏好。当误差修正项μt-1>0.0654时,即Rt-1>0.073+0.53πt-1-0.0006(t-1)+0.0654时,利率向长期均衡的调整速度明显高于μt-1≤0.0654时的调整速度。说明我国中央银行调整利率存在非对称偏好,即中央银行更倾向于采取扩张性的利率政策来刺激经济增长,适度诱导通货膨胀。相反,在治理通货膨胀时并不青睐于紧缩性的利率政策。这主要是由于目前我国的利率水平已经偏高,如果仍然采用调高利率的手段来控制通货膨胀,会拉大国内外的利差,国际上对人民币升值和国内资产价格上涨的预期将进一步加强,外资和热钱进入中国的动力将进一步加大,这必然导致资本金融项目顺差的扩大和外汇储备的持续快速增长,不利于我国改变国际收支失衡的局面,也不利于资金流动性过剩问题的解决;另外,受美国次级债危机的影响,2008年我国股市低迷,利率水平的提高将加重居民的利息负担,加大金融业的系统风险,对经济也将造成不利影响。
最后,通货膨胀呈现“弱外生性”。由通货膨胀的误差修正模型估计结果可以看出 (见式(12))。无论在区制1还是在区制2上,误差修正项的系数均不显著,表明在名义利率与通货膨胀的二元系统中,通货膨胀具有“弱外生性”⑥。因此,现阶段利率政策对于抑制目前的高通胀存在一定的难度,还应该辅以其他的货币政策,必要时可采取行政手段进行价格干预。
注释:
①将数据起始点选择1996年主要是由于人民银行1996年才建立全国银行同业拆借市场,选择月度数据是为了增加结论的灵敏性和样本数量。
②本文也采用基于VAR模型的Johasen协整检验方法对上述两变量进行协整检验,检验结果与E-G两步法的检验结果是一致的。为了研究残差性质,故本文只给出E-G两步法的检验结果。
③实际上,上述残差序列为一趋势平稳过程 (检验结果略),但只有残差序列为严格意义上的平稳过程时,“费雪效应”才成立。
④事实上,模型滞后阶数取1、2、4、5、6时,门限值的估计量都很接近。最终的名义利率与通货膨胀的TVECM模型的误差修正项的系数估计值也很相近,故本文只给出滞后阶数为1的TVECM模型的估计结果。
⑤由于模型(3)要对冗余参数 (nuisance parameter)进行识别,单个变量显著性检验的统计量不再服从标准的分布,因此没有给出参数的统计量。
⑥在通货膨胀的误差修正模型中,除在第1区制上的通货膨胀差分的滞后项相对显著外,其余名义利率与通货膨胀的滞后项均不显著。
[1] 刘金全、郭整风、谢卫东.时间序列的分整检验与“费雪效应”机制分析 [J].数量经济与技术经济研究.2003(4):59-63.
[2] Balke,N.S.,Fomby,T.B..Threshold cointegration[J].International Economic Review 1997(3):627-645.
[3] Baum,C.F.,Barkoulas,J.T.,Caglayan,M..Nonlinear adjustment to purchasing power parity in the post-Bretton Woods era[J].Journal of International Money and Finance.2001(20):379-399.
[4] Bonham,C.S.Correct Cointegration Test of the Long Run Relationship Between Nominal Interest and Inflation[J].Applied Economics.1991(23):1487-1492.
[5] Caner,M.,Hansen,B.E..Threshold Autoregression with a Unit Root[J].Econometrica.2001 (6):1555-1596.
[6] Chan,K.S.and Tong,H..On Likelihood Ratio Tests for Threshold Autoregression[J].Journal of the Royal Statistical Society.1990(3):469-476.
[7] Chan,K.S..Consistency and Limiting Distribution of the Least Squares Estimator of a Threshold Autoregressive Model[J].The Annals of Statistics.1993(1):520-533.
[8] Cooray,Arusha.The Fisher effect:a review of the literature[M].Macquarie economics research papers,2002.
[9] Enders,W.,Falk,B..Threshold-autoregressive,median-unbiased,and cointegration tests of purchasing power parity[J].International Journal of Forecasting.1998(14):171-186.
[10] Enders,W.,Siklos,E.P..Cointegration and Threshold Adjustment[J].Journal of Business&Economic Statistics.2001(2):166-176.
[11] Engle,Granger.Co-integration and Error Correction:Representation,Estimation,and Testing[J].Econometrica.1987(2):251-276.
[12] Fama,E.F..Short Term Interest Rates as Predictors of Inflation[J].American Economic Review.1975(65):269-282.
[13] Fisher,Irving.The Theory of Interest[M].Macmillan,New York,1930.

