基于Lyapunov理论的运营期地铁隧道沉降稳定性分析

李支彬,黄 腾,李桂华

(河海大学地球科学与工程学院,江苏南京 210098)

目前对运营期地铁隧道沉降稳定性的研究尚处于初步阶段,主要从统计学、工程理论与实践的方法入手,根据沉降监测数据或地区的普遍规律对运营期地铁隧道沉降进行稳定性评判。然而,在不同的地质环境和工况条件下,隧道沉降原因和规律有较大差别,仅依靠单一的沉降监测数据或地区的普遍规律进行评判有失偏颇,应在弄清沉降机理、明晰沉降趋势、综合考虑各类影响因素的基础上建立科学合理且具有通用性的评判模型才能较好地解决此问题。笔者从系统论的思路入手,将运营期地铁隧道沉降作为一个动态系统,将影响地铁隧道沉降稳定性的主要因素作为状态变量,根据观测资料反演地铁隧道沉降系统的动力学模型,然后依据基于Lyapunov理论的运营期地铁隧道沉降稳定性判据,判定地铁隧道沉降的稳定性。

1 运营期地铁隧道沉降动力学模型

1.1 反演动力学模型的方法

动力学模型的建立方法主要有根据系统的内部构成及物理机理建立动力学模型和根据监测资料反演动力学模型。由于人们对地铁隧道沉降变形体系统的内部构成和物理机理缺乏足够的了解,所以通常利用反演的方法建立动力学模型[1]。

利用观测资料反演变形体系统动力学模型的原理是监测变形体系统获得的大量观测资料在一定程度上包含了系统的动力学性质,体现了系统演变过程中不同时刻的状态,将观测数据看作是系统实际轨迹的一系列离散值,进而通过反演得到变形体系统的动力学方程。变形体系统的一般动力学方程为

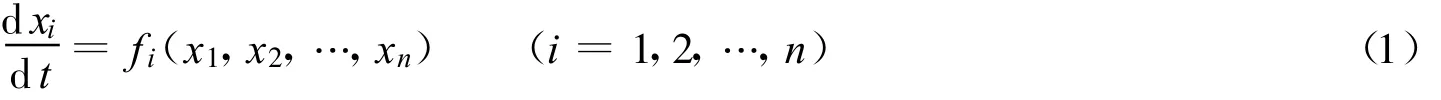
式中：n——动力学方程中的变量数;xi——状态变量,设xi的一系列观测值为xi(t0+jΔt),其中j=1,2,…,m,i=1,2,…,n;t0——起始观测时间;Δt——观测时间间隔(Δt可为不等间隔);m——观测数据离散值个数。

设t0=0,将式(1)写成差分的形式：

则式(2)可由观测序列di,j组成m-1个观测方程。若设fi(x1,x2,…,xn)中有K个参数Pk(k=1,2,…,K),并具有如下的多项式形式：

则式(2)可以写成矩阵形式：

其中

根据最小二乘准则,可以写出以下正则方程：

若GTG是非奇异矩阵,则有

若GTG是奇异矩阵,或者接近奇异,则对误差特别敏感,而G本身并不十分准确,会有较大误差,可采用奇异值分解法(SVD)来解决此问题,限于篇幅,在此不赘述。

1.2 运营期地铁隧道沉降动力学模型

根据某市运营期地铁隧道工程地质条件及土力学知识[2-6],将地下水位h、地下水位的平方h2、列车荷载Nb、地面累积沉降量H、建筑物荷载 η和降雨量P作为主成分分析因子,通过主成分分析法进行成因分析,选取对运营期地铁隧道沉降贡献率最大的h2,Nb,H作为主要影响因素。对于不同工程地质条件下的地铁隧道,其沉降机理和影响因素均不同,需根据实际观测资料进行成因分析并选取主要影响因素。

选取h,Nb,H这3个主要影响因素和隧道累积沉降量S作为地铁隧道沉降系统的状态变量,分别用变量x1,x2,x3,x4来代替,在满足工程精度的前提下,为避免各状态变量间相关性的重复导致动力学方程复杂化和相关关系的冗余,建立动力学模型：

式中ai0,ai1,ai2,ai3,ai4为参数。

根据地铁观测资料,利用上述反演方法确定式(7)中各项系数。为衡量反演效果,计算动力学模型中预测值与实际值的标准偏差r和复相关系数R2,用以检验反演的动力学模型是否满足精度要求。

2 基于Lyapunov理论的运营期地铁隧道沉降稳定性

Lyapunov理论关于稳定性判别的方法有2种：(a)级数展开法;(b)Lyapunov直接法,即通过Lyapunov函数V(x1,x2,…,xn)来判别系统运动的稳定性。然而,目前构造Lyapunov函数还存在一定的困难,在满足要求的前提下,级数展开法仍为最重要的方法[7-9]。

2.1 稳定性及平衡态

稳定性是系统的一个动态属性[10]。稳定的系统应具有这样的性能：在它受到外界的扰动后,虽然其原平衡态被打破,但在扰动之后有能力自动返回原平衡态或者趋于另一新的平衡态继续工作。平衡态是使得系统静止不动的状态。变形体系统不可能处于绝对的静力平衡状态,在外力的作用下变形体系统的任何变化都可视为一种运动,平衡态只是运动状态的一种特殊情况。Lyapunov理论是研究系统平衡态附近的运动变化问题。平衡态附近某充分小邻域内所有状态的运动最后都趋于该平衡态,则称该平衡态是渐进稳定的;若不能限定在平衡态附近某个邻域内运动,则称该平衡态是不稳定的;若能维持在平衡态附近某个邻域内运动变化,则该平衡态是稳定的。

2.2 基于Lyapunov理论的运营期地铁隧道沉降稳定性判据

考虑运营期地铁隧道沉降动力学模型(式(7)),将其写成向量形式：

设平凡解(零解)xe是一平衡态,即

在平衡态xe附近把式(7)展开成Taylor级数并写成向量形式：

3 工程实例分析

根据某市运营期地铁隧道K1+033断面的1～7期观测数据,由最小二乘法求得其动力学方程参数aik(k=0,1,2,3,4)。为衡量反演效果,计算动力学模型中x1,x2,x3,x4预测值与实际值的标准偏差和复相关系数,结果分别为可知反演效果较好。

1234-0.1491。在平衡态处把式(7)按Taylor级数展开,前7期观测数据所对应的Jacobi矩阵A为

A的特征值的实部分别为λ1=0.6573,λ2=0.6573,λ3=2.7754,λ4=-1.1955,最大值为2.7754。由基于Lyapunov理论的运营期地铁隧道沉降稳定性判据可判定该平衡态不稳定。

同理,依据观测资料中前8期、前9期、前10期、前11期数据分别反演地铁隧道沉降动力学模型,计算动力学模型中各变量的预测值与实际值的标准偏差和复相关系数,其中最大标准偏差为0.0628,最小复相关系数为0.8135,表明各动力学模型反演效果良好。求解各动力学模型的平衡态,计算得出各反演动力学方程的Taylor级数展开式Jacobi矩阵A的特征值。图1为各动力学模型Jacobi矩阵A特征值的实部最大值随观测期数的变化,由图1可知,对应于前8期、前9期、前10期、前11期观测数据的A的特征值实部最大值分别为-0.2296,-0.2716,1.4705,0.5523。

依据运营期地铁隧道沉降稳定性判据,由图1得出：前7期地铁隧道沉降系统处于不稳定状态;前8期和前9期地铁隧道沉降系统处于渐近稳定状态,并且在不受外力干扰时各状态变量将逐渐趋于平衡态;前9期至前10期地铁隧道沉降系统由渐近稳定状态转变为不稳定状态;前10期至前11期特征值的实部最大值减小但仍大于零,表明地铁隧道沉降系统处于不稳定状态,但稳定性随观测期数的增加而逐渐增强。

该地铁隧道的实际运营情况是前7期处于运营初期,前8期和前9期地铁隧道地质环境相对稳定,前9期至前10期距地铁约68m处正在开挖基坑,实际情况与上述稳定性分析结果相吻合。另外,对其他断面及不同地质条件下的运营期地铁隧道进行沉降稳定性分析,实际情况与稳定性分析结果均基本吻合,说明采用基于Lyapunov理论的稳定性分析方法分析运营期地铁隧道沉降的稳定性是合理的。

图1 各动力学模型Jacobi矩阵A特征值的实部最大值随观测期数的变化Fig.1 Maximum value of real part of matrix A's eigenvalues varying with time for various dynamic models

4 结 论

a.基于Lyapunov理论的运营期地铁隧道沉降稳定性分析方法从系统、整体的观点出发,利用主成分分析法选取实际工程地质条件下导致地铁隧道沉降的主要因素为状态变量,根据实际观测资料反演建立动力学模型,实测计算结果表明该模型能够很好地反映地铁隧道的沉降机理,对于运营期地铁隧道沉降的稳定性分析具有良好的普适性。

b.在不受外力或所受外力微小时,所建立的动力学模型各状态变量趋于平衡态,各状态变量在平衡态处的值及稳定性分析结果可为运营期地铁隧道的安全运营与决策提供理论依据。

[1]张正禄,黄全义,文鸿雁,等.工程的变形监测分析与预报[M].北京：测绘出版社,2007：51-104.

[2]陈晓平,朱鸿鹄,张芳枝,等.软土变形时效特性的试验研究[J].岩石力学与工程学报,2005,24(12)：2142-2148.(CHEN Xiaoping,ZHUHonghao,ZHANG Fangzhi,et al.Experimental study on time-dependent deformation of soft soil[J].Chinese Journal of RocKMechanics and Engineering,2005,24(12)：2142-2148.(in Chinese))

[3]成枢.地面沉降变形预计模型与监测技术研究[D].青岛：山东科技大学,2006.

[4]叶耀东,朱合华,王如路.软土地铁运营隧道病害现状及成因分析[J].地下空间与工程学报,2007,3(1)：157-166.(YE Yaodong,ZHU Hehua,WANG Rulu.Analysis on the current status of metro operating tunnel damage in soft ground and its causes[J].Chinese Journal of Underground Space and Engineering,2007,3(1)：157-166.(in Chinese))

[5]李桂华.漫滩软土地铁隧道运营期沉降监控关键技术研究[D].南京：河海大学,2011.

[6]LI Dingqing.Cumulative plastic deformation for fine-grained subgrade soils[J].Journal of Geotechnical Engineering,1996,122(12)：1006-1013.

[7]廖晓昕.稳定性的理论方法和应用[M].武汉：华中科技大学出版社,1999：220-361.

[8]LIAPUNOV A M.The general problem of the stability of motion[M].London：CRCPress,1992：21-37.

[9]刘春美.Lyapunov方法在系统稳定性理论上的应用[D].长春：东北师范大学,2010.

[10]杨彩红,王永岩,李剑光.水对边坡力学系统稳定性的影响[J].煤矿开采,2007,12(1)：8-13.(YANG Caihong,WANG Yongyan,LIJianguang.Influenceof water onthestability of slopemechanics system[J].Coal Mining Technology,2007,12(1)：8-13.(in Chinese))

[11]史志伟,吴根兴.飞机大迎角滚转运动频率域建模与稳定性分析[J].空气动力学学报,2000,18(3)：307-314.(SHI Zhiwei,WU Genxing.Unsteady aerodynamics modeling of arolling aircraft at high angleof attacKand analysis of stabilit[J].Acta Aerodynamica Sinic,2000,18(3)：307-314.(in Chinese))

[12]吴中如,潘卫平.应用李雅普诺夫函数分析岩土边坡体的稳定性[J].水利学报,1997,28(8)：29-33.(WU Zhongru,PAN Weiping.Stability analysis of geotechnical slopes by Ljapunov function and its one-time approximate method[J].Journal of Hydraulic Engineering,1997,28(8)：29-33.(in Chinese))