基于Delaunay三角网的三维Voronoi单胞体积计算

丁道红,章 青

(1.河海大学水文水资源与水利工程科学国家重点实验室,江苏南京 210098;2.河海大学力学与材料学院,江苏南京 210098)

Voronoi单胞是以自然相邻插值法进行形函数构造的自然单元法的基础[1-2]。自然单元法形函数的构造方法有Sibson法[3]和Laplace法[4]2种,其中Sibson法是以插值点对应于某一结点的二阶Voronoi单胞的勒贝格测度与插值点的一阶Voronoi单胞的勒贝格测度的比值作为形函数。三维Voronoi单胞的勒贝格测度即为Voronoi单胞的体积,目前关于Voronoi单胞体积的计算最常用的方法是Lasserre方法[5-8]。Lasserre方法是在已知凸多面体控制方程的前提下,通过递推公式求得凸多面体的体积。该方法因具有简单可行、操作方便等优点而得到广泛的应用,但该方法在应用过程中要求控制方程不能存在冗余的方程。本文在与Voronoi单胞相对应的Delaunay三角网的启示下,通过Delaunay三角网将三维Voronoi单胞划分成若干个不重叠且充满Voronoi单胞的四面体,从而可简单地通过四面体的体积计算得到Voronoi单胞的体积。

1 Voronoi单胞

对于Voronoi单胞的概念[9],可通过数学方式进行描述。记Rn空间上任意2点xI和xJ的欧氏距离为d(xI,xJ),设P={x1,…,xn}为Rn空间上任意n个互异的点,则与其中任意一点xI对应的Voronoi单胞的定义为

二阶Voronoi单胞是在Rn空间上任意n个互异的点P={x1,…,xn}的基础上,增加一新的待插值点x′,形成新的一阶Voronoi单胞,其中结点xI为插值点x′的自然邻点,结点xI的二阶Voronoi单胞为结点xI的一阶Voronoi单胞与插值点x′的一阶Voronoi单胞重叠的部分,即

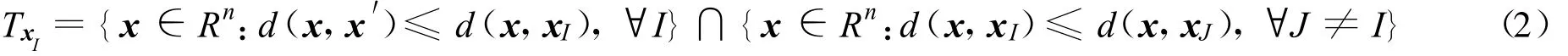
将具有公共边界的Voronoi单胞所对应的结点称为自然邻点,其公共边界为该2点的中垂面(二维问题为2点的垂直平分线),即2自然邻点xI和xJ的Voronoi单胞公共边界所在的平面(或直线)L为

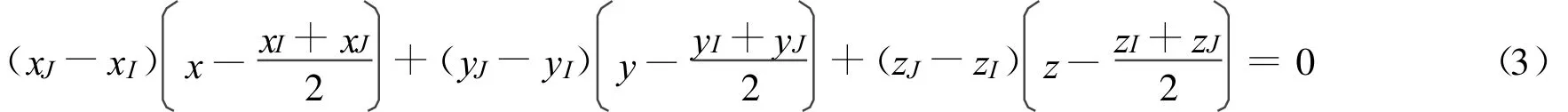
其法线方向为结点xI指向xJ。与结点xI对应的Voronoi单胞在平面(或直线)L的结点xI所在的一侧,即结点xI对应的Voronoi单胞满足

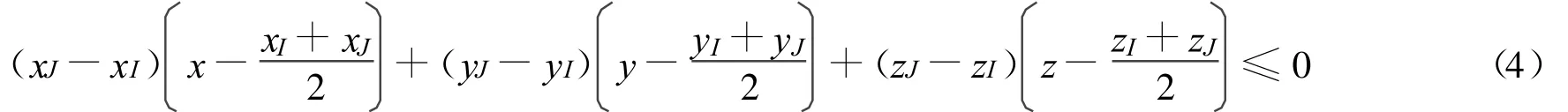
假设结点xI(xI,yI,zI)为插值点xp(xp,yp,zp)的1个自然邻点,与结点xI(xI,yI,zI)对应的自然邻点共有m个,分别为(x1,y1,z1),…,(xm,ym,zm),则与结点xI对应的二阶Voronoi单胞可写成

令

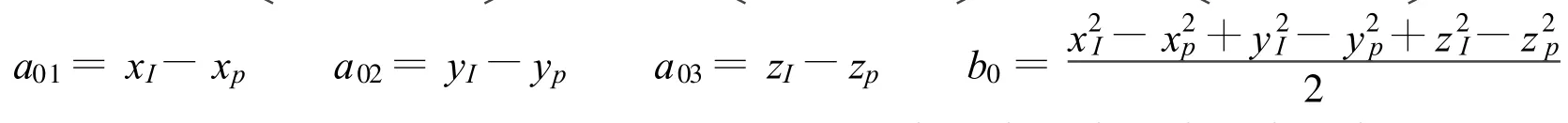
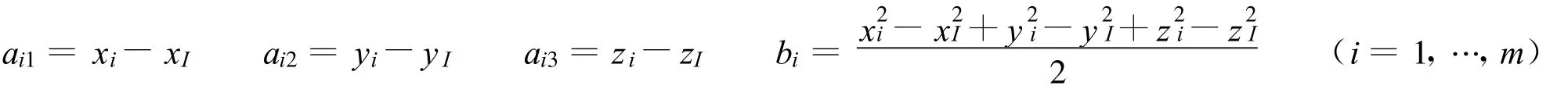
则式(5)可写为

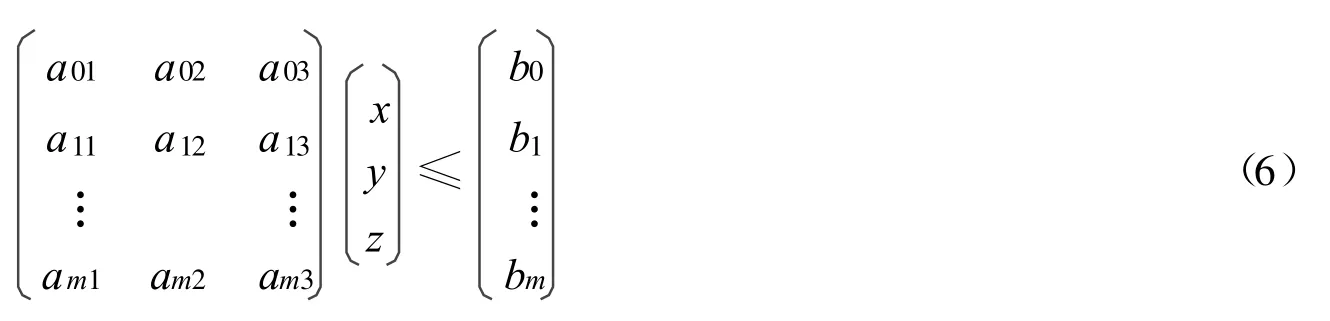
式(6)描述了二阶Voronoi单胞的控制域,若能得到二阶Voronoi单胞的顶点,则可通过Delaunay三角网将控制域划分成若干个小域进行分析。因此若要得到二阶Voronoi单胞的勒贝格测度,首先需要得到二阶Voronoi单胞的顶点。二阶Voronoi单胞的顶点是边界的交点,即式(6)取等号时所得的满足式(6)的点。对于n维空间问题,通过联立式(6)中n个方程,建立1个新的方程组

若|A|≠0,则式(7)必有解

若x=A-1b满足式(6),则为二阶Voronoi单胞的1个顶点。

2 Delaunay三角网

Delaunay三角网的概念是建立在Voronoi单胞基础之上的。将具有公共边界的Voronoi单胞所对应的结点连接所得到的三角形,称作Delaunay三角形,将Rn空间上任意n个互异的点通过Delaunay三角形划分,可形成Delaunay三角网。

文献[10]证明了Delaunay三角网具有如下性质。

a.唯一性：不论从区域何处开始构建,最终都得到一致的结果。

b.最优性：任意2个相邻三角形形成的凸四边形的对角线如果可以互换,那么2个三角形6个内角中最小的角度不会变大。

c.最规则：如果将三角网中每个三角形的最小角进行升序排列,则Delaunay三角网的排列得到的数值最大。

d.具有凸多边形的外壳：三角网最外层的边界形成1个凸多边形的外壳。

以上这些性质保证了Delaunay三角网所划分的区域不具有重叠部分,且能覆盖结点所占的凸区域。

目前关于Delaunay三角网划分的方法很多[11-12],如Lawson算法、Bowyer-Watson算法等。此外,一些商业软件具有成熟的Delaunay三角网划分的功能,如MATLAB软件中,可通过Delaunay命令进行相关工作。

在三维问题中,通过Delaunay三角网划分所得的基本体为四面体,四面体的体积可通过简单的几何方法得到,如已知某四面体的4个顶点分别为(x1,y1,z1),(x2,y2,z2),(x3,y3,z3),(x4,y4,z4),则该四面体的体积为

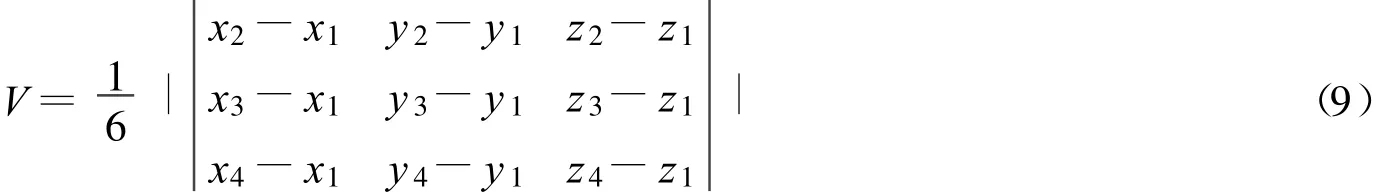
3 算 例

已知三维空间8结点1(0,0,0),2(1,0,0),3(1,0,1),4(0,0,1),5(0,1,0),6(1,1,0),7(1,1,1),8(0,1,1),插值点xp(0.7236,0.1382,0.1382),则结点6为插值点的自然邻点。结点6的自然邻点有3个,分别为2,5,7。结点6的二阶Voronoi单胞为

其中

通过式(10)中任取3个方程并取等号进行联立方程,代入上式进行判断是否符合要求,可得结点6的二阶Voronoi单胞的顶点为(0.5,0.5,-1.0854),(1.2927,0.5,0.5),(0.5,0.7542,0.5),(0.5,0.5,0.5)共4个结点,通过Delaunay三角网,可划分成1个四面体,通过式(8)可知其体积为0.0533。

4 结 语

在已知Voronoi单胞顶点的前提下,利用Delaunay三角网将Voronoi单胞划分成若干四面体,通过求解四面体的体积得到Voronoi单胞的体积。该方法具有原理简单、可行性强、理解性好等优点。

此外,该方法不仅可以应用于三维Voronoi单胞的体积计算,对于任意1个已知边界顶点的凸多面体均可应用该方法进行体积的计算。

[1]BRAUN J,SAMBRIDGEM.A numerical method for solving partial differential equations on highly irregular evolving grids[J].Nature,1995,376：655-660.

[2]SUKUMAR N,MORAN B,BELYTSCHKO T.The natural element method in solid mechanics[J].International Journal for Numerical Methods in Engineering,1998,43(5)：839-887.

[3]SIBSON R.A brief description of natural neighbour interpolation[G]//BARNETT V.Interpreting Multivariate Data.New York：Wiley,1981：21-36.

[4]BELIKOV V V,SEMENOV A Y.Non-Sibsonian interpolation on arbitrary system of points in Euclidean space and adaptive isolines generation[J].Applied Numerical Mathematics,2000,32(4)：371-387.

[5]LASSERRE JB.An analytical expression and an algorithm for the volume of a convex polyhedron inRn[J].Journal of Optimization Theory and Applications,1983,39(3)：363-377.

[6]LASSERREJB.A laplace transform algorithm for the volume of a convex polytope[J].Journal of the ACM,2001,48(6)：1126-1140.

[7]王建华,张英新,高绍武.三维弹塑性自然单元法算法实现[J].计算力学学报,2006,23(5)：594-598.(WANG Jianhua,ZHANG Yingxin,GAO Shaowu.The computational methods of natural element method in three dimensional elasto-plastic analysis[J].Chinese Journal of Computational Mechanics,2006,23(5)：594-598.(in Chinese))

[8]江涛,章青.基于Lasserre算法的自然单元法形函数计算[J].力学与实践,2008,30(4)：1-5.(JIANG Tao,ZHANGQing.The shape functions in the natural element method based on Lasserre's algorithm[J].Mechanics in Engineering,2008,30(4)：1-5.(in Chinese))

[9]杨永清,冯钧,王志坚.基于Voronoi图的复杂对象空间方位关系的推理计算[J].河海大学学报：自然科学版,2008,36(3)：414-417.(YANG Yongqing,FENG Jun,WANG Zhijian.Reasoning and calculation of spatial direction relationship between complex objects based on Voronoi diagram[J].Journal of Hohai University：Natural Sciences,2008,36(3)：414-417.(in Chinese))

[10]SEIDEL R.The upper bound theorem for polytopes：an easy proof of its asymptotic version[J].Computational Geometry,1995,5(2)：115-116.

[11]王建华,徐强勋,张锐.任意形状三维物体的Delaunay网格生成算法[J].岩石力学与工程学报,2003,22(5)：717-722.(WANG Jianhua,XUQiangxun,ZHANG Rui.Delaunay algorithm and related procedure to generate the tetrahedron mesh for an object with arbitrary boundary[J].Chinese Journal of RocKMechanics and Engineering,2003,22(5)：717-722.(in Chinese))

[12]WATSON D F.Computing then-dimensional delaunay tessellation with application to Voronoi polytopes[J].The Computer Journal,1981,24(2)：167-172.