重塑土不排水剪切应力-应变关系预测

倪钧钧,吴学春,张立志,王庶懋,陶崇福

(1.河海大学岩土工程研究所,江苏南京 210098;2.南水北调东线江苏水源有限责任公司,江苏南京 210029;

3.山东临沂岸堤水库管理处,山东 临沂 276000;4.华东电力设计院,上海 200063;5.安徽省地震局,安徽 合肥 230031)

随着我国对港口航道通航需求量的增多,每年都要进行大规模的疏浚工程,会产生大量的疏浚淤泥。在疏浚淤泥造地工程设计中重塑土强度性状是1个重要参数,所以研究其应力-应变关系特性尤为重要。重塑土由于受围压、初始含水率等条件的影响,其工程力学性质很复杂[1],因此在实际工程设计中迫切需要建立可靠实用的重塑土应力-应变关系预测模型。

许多学者对重塑土应力-应变关系的归一化特性进行了系统的研究[2-6],并提出了各种形式的函数来模拟试验曲线,如：抛物线模型、双曲线模型、双折线模型等。其中运用最广泛的是Konder提出的双曲线模型[7],该模型归一化效果的好坏主要取决于归一化因子的选择。在双曲线模型的基础上李作勤[6]用围压 σ3作为归一化因子;张勇等[8]认为用主应力差渐近值(σ1-σ3)ult作为标准归一化因子可以很好地模拟软土的归一化特性。土的应力-应变关系是土的固有属性,由其本身的物理性质和矿物成分确定。由于传统的模型以诸多假设为基础,且仅通过改变简单的数学公式的参数来反映不同岩土材料的应力-应变关系,因此,其具有明显的局限性。而BP神经网络在描述高度非线性关系方面具有很大的优势,无需任何假定便可根据数据样本自动训练得到参数并建立数学模型,所建立的预测模型有较高的拟合和预测精度,对实际工程具有很大的指导意义。

笔者基于多组重塑土室内三轴固结不排水剪切试验,设计BP神经网络的输入、输出变量,并建立重塑土三轴不排水剪切应力-应变关系的BP神经网络预测模型,最后将此模型的预测结果与试验结果及基于双曲线模型的归一化应力-应变关系的预测结果进行对比,分析此模型的优缺点。

1 特定含水率下应力-应变曲线的预测

分析所用的试验样品来自温州河道疏浚淤泥,其物理力学参数如下：相对密度Gs=2.72,液限WL=78.9%,塑限WP=34.1%,塑性指数IP=44.8%,黏粒(粒径d＜0.005mm)的质量分数为63.2%,粉粒(d的范围为0.005～0.075mm)的质量分数为35.6%,砂粒(d的范围为0.075～2.000mm)的质量分数为1.2%。在实验室内,对初始含水率w0=75%的温州重塑土进行人工压制,得到直径d=39.1mm、高度h=80.0mm的实心圆柱状土试样。在试样装上应变控制式静三轴仪前,先采用抽气饱和法对其进行真空抽气饱和,真空抽气饱和后,试样饱和度可以达到98%以上。

通过室内常规三轴固结不排水剪切试验(剪切速率设定为0.073mm/min),得到w0=75%的温州重塑土在固结围压分别为25kPa,50kPa,100kPa,150kPa,200kPa下的应力-应变曲线。根据25kPa,50kPa,100kPa,200kPa下的应力-应变曲线进行拟合并建立预测模型,在此基础上对围压为150kPa下的应力-应变曲线进行预测,并与试验结果进行对比。

1.1 基于双曲线模型的应力-应变曲线预测

Konder等认为常规静三轴试验的(σ1-σ3)～ε1关系可以近似用双曲线方程式(1)来表示[7]：

式中：ai——某不变固结围压下的主应力差渐近值(σ1-σ3)ult的倒数;bi——初始切线模量E0i的倒数。

式(1)变形可得

不同固结围压(25kPa,50kPa,100kPa,200 kPa)下的ε1/(σ1-σ3)～ε1试验关系曲线如图1所示。由图1可知4种不同围压下的ε1/(σ1-σ3)～ε1关系都表现出良好的线性相关性,用式(2)对图1中的应力-应变关系进行拟合,得到参数ai和bi的值,见表1。根据表1有关参数,主应力差渐近值(σ1-σ3)ult与固结围压 σ3之间的关系如图2所示,可以用式(3)表示：

图1 等压固结不排水剪切应力-应变关系Fig.1 Stress-strain curves in consolidated undrained test

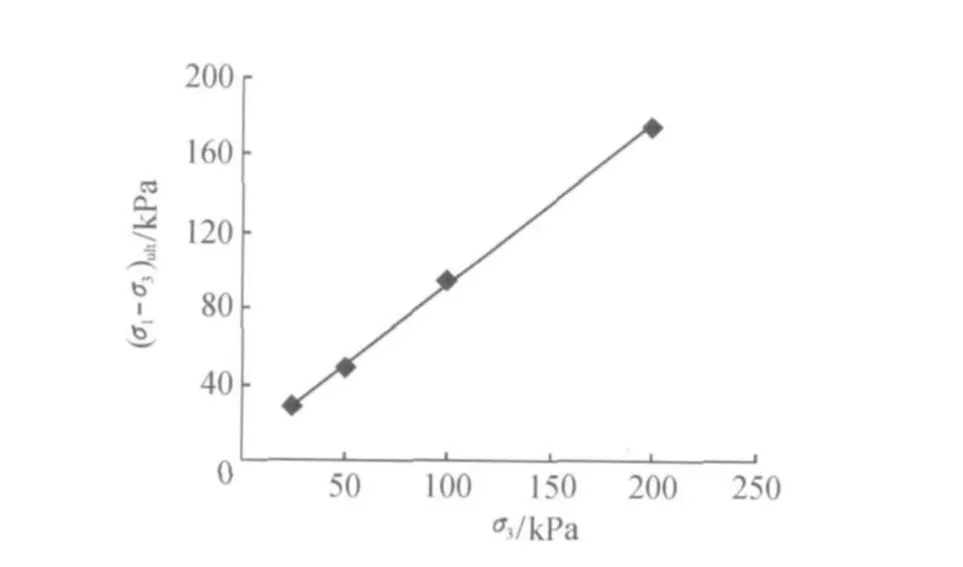
图2 (σ1-σ3)ult～ σ3的关系Fig.2 Relationship between(σ1-σ3)ult andσ3

表1 拟合得到的参数Table1 Parameters obtained by fitting experimental data

在式(3)和双曲线模型的基础上对温州重塑土固结不排水剪切应力-应变特性进行归一化分析。选用2种归一化因子,即 σ3和(σ1-σ3)ult。若以σ3为归一化因子,则归一化结果如图3(a)所示,对应的归一化公式为

由式(4)拟合不同围压下的(σ1-σ3)～ε1关系曲线,如图3(b)所示。

图3 σ3为归一化因子的应力-应变归一化结果Fig.3 Normalized stress-strain curves with normalized factorσ3

以(σ1-σ3)ult作为归一化因子,则不同围压下的 ε1/(σ1-σ3)～ε1关系归一化结果如图4(a)所示。由图4(a)可知,其具有较好的归一化特性,且对应的归一化公式为

将式(3)代入式(5)得

由式(6)拟合不同围压下的(σ1-σ3)～ε1关系曲线,如图4(b)所示。

图4 (σ1-σ3)ult为归一化因子的应力-应变归一化结果Fig.4 Normalized stress-strain curves with normalized factor(σ1-σ3)ult

由以上分析可知,用σ3作为归一化因子,对温州重塑土的应力-应变特性进行归一化,其归一化效果较差,对应的拟合曲线与试验值差别较大,对围压为150kPa下的应力-应变曲线的预测结果与试验值也有明显的偏差。与 σ3作为归一化因子相比,用(σ1-σ3)ult作为归一化因子的归一化效果较好,在此基础上建立的应力-应变预测模型能够较好地描述温州重塑土在不同围压下的应力-应变关系。

由图3(b),4(b)可知,当围压较大时,峰值前应力明显高于实际应力,即拟合所得曲线的压缩模量比实际的大,这样的成果应用于实际工程会导致计算沉降值偏小,而且对围压150kPa下的应力-应变曲线预测结果与试验值仍存在一定的偏差。

1.2 基于BP神经网络的应力-应变关系预测

BP神经网络[9-11]是一种典型的前馈型网络,由输入层、隐含层和输出层组成,各层之间采用全部连接方式,但同一层单元之间不存在相互连接。该网络算法的原理是通过已得网络输出误差的反向传播,及时调整和修改网络的连接权值,使网络误差达到最小。输入信号经隐含层的作用函数后,把结果传输到输出层,如果在输出层得不到期望的输出则转入反向传播,将误差信号沿原通路返回,并通过修改各层神经元之间的权值使误差最小。由BP神经网络的建模过程可知,模型没有对输入、输出变量的关系做任何假定,网络参数由学习样本的训练得到,避免了建立数学模型的困难。

本文建立3层BP神经网络模型,设置输入层的节点数为2,输出层的节点数为1,输入节点为轴向应变ε1和固结围压σ3,输出节点为主应力差(σ1-σ3)。设置传输函数为非线性双曲正切S型函数,输出层神经元采用纯线性函数,学习函数为附加动量因子的梯度下降权值学习函数,经过调试确定隐含层单元数为5时最佳,拟合结果如图5所示。

为了与上述归一化模型进行对比,同样以 σ3=25 kPa,50kPa,100kPa,200kPa的应力-应变曲线为训练样本,辨识神经网络模型的结构参数。利用训练好的网络对训练样本进行模拟,然后用所建立的模型预测围压为150kPa下的应力-应变曲线,并与试验结果进行比较。从图5可以看出,不论是拟合结果还是对150kPa围压下应力-应变曲线的预测结果都与试验结果比较吻合,与双曲线预测模型拟合效果相比误差更小,也更可靠。

图5 BP神经网络的拟合、预测曲线与试验值的比较Fig.5 Comparison of experimental curves and fitting and predicted curves based on BP neural network

2 任意含水率下应力-应变关系曲线的预测

在双曲线模型基础上建立的归一化公式只考虑特定含水率下的重塑土应力-应变关系,没有反映初始含水率变化对重塑土应力-应变关系的影响。而BP神经网络在模拟和预测相关的非线性和不确定性问题时具有独特的优越性,能够突破传统模型的局限,可以考虑不同初始含水率下重塑土的应力-应变关系。

根据BP神经网络拟合及预测的需要,选用上海金桥地区4层淤泥质重塑土在4种不同初始含水率(分别为21%,25%,28%,31%)下的应力-应变关系曲线[12]。该土的基本物理参数如下：密度 ρ=1.71g/cm3,孔隙比e=1.42,塑限WP=67.8%,塑性指数IP=21.2%。其中初始含水率w0为21%,25%,31%的应力-应变曲线如图6所示。

图6 BP神经网络拟合曲线与试验值的比较Fig.6 Comparison of experimental curves and fitting curves based on BP neural network

根据BP神经网络原理,建立3层BP神经网络模型。选取初始含水率w0、围压 σ3以及轴向应变 ε1为网络的基本输入变量,则输入层的节点数为3;输出节点设为主应力差(σ1-σ3),则输出层的节点数为1。设置传输函数为非线性双曲正切S型函数,输出层神经元采用纯线性函数,学习函数采用附加动量因子的梯度下降权值学习函数,经过调试确定隐含层单元数为5时最佳。

训练BP神经网络时采用3组应力-应变曲线,为w0=21%,25%,31%的重塑土皆在固结围压为50kPa,100kPa,150kPa,200kPa时所得的应力-应变曲线。然后用训练得到的模型对初始含水率为28%的重塑土试样在固结围压为50kPa,100kPa,150kPa,200kPa下的应力-应变关系进行预测,并与试验所得的应力-应变曲线进行比较。

BP神经网络的学习,主要通过对样本的反复训练来建立模型,训练结果直接决定所建立模型的质量。在进行BP神经网络学习、训练前,需要对原始的样本数据进行标准化转换,将其所有数据都归一化到[0,1]之间,在最后结果输出时再将结果反归一化。

为了验证训练效果,对BP神经网络所建立的模型进行检验。由图6可知,该BP神经网络模型能够很好地拟合试验所得结果。图7为预测曲线与试验结果的比较,可以看出,所得预测曲线较光滑,并且能够较好地吻合于试验结果,预测结果的最大误差出现在200kPa时的应力-应变曲线的中段,相对误差为8.84%,对于实际工程而言是可以接受的。

通过分析可知,BP神经网络模型能较好地拟合重塑土随初始含水率变化时在各种围压下的应力-应变关系曲线,并且此模型能较好地预测其他初始含水率的重塑土在任意围压下的应力-应变关系曲线,从而弥补室内试验费时费力、所得试验数据量不足等缺陷。

图7 初始含水率为28%时的预测曲线和实测曲线Fig.7 Comparison of experimental curves and predicted curves with initial water content of 28%

3 结 论

a.基于双曲线模型及BP神经网络模型对重塑土固结不排水剪切应力-应变曲线进行预测,结果表明,采用(σ1-σ3)ult作为归一化因子的双曲线模型比以 σ3为归一化因子的双曲线模型预测效果好;BP神经网络模型比双曲线模型的预测精度高。

b.BP神经网络可以模拟应力-应变全过程曲线,拟合曲线与试验结果较为吻合;基于双曲线函数的应力-应变归一化模型,在达到峰值强度前,拟合所得的压缩模量比实际的大,容易导致实际工程中计算沉降值偏小。

c.传统的基于双曲线模型理论只能对某一特定含水率下的应力-应变曲线进行预测,而BP神经网络模型可以预测不同初始含水率下的应力-应变曲线。

d.双曲线模型是基于试验并建立在一定的数学假设之上,对高围压下重塑土的应力-应变曲线进行模拟具有一定的偏差;BP神经网络模型无需任何假设,可以根据已有的试验数据自动生成网络参数,避免了建立数学模型的困难,拟合、预测的精度更高,结果更可靠。

[1]黄文熙.土的工程性质[M].北京：中国水利水电出版社,1983.

[2]邵军义,朱珊.黏性土应力应变关系的归一化弹性模量及其应用[J].鞍山钢铁学院学报,1997,20(4)：42-45.(SHAO Junyi,ZHUShan.On the normalization and the modulus of elasticity relating the stress to the strain of the clay soil and its application[J].Journal of Anshan Institute of Iron and Steel Technology,1997,20(4)：42-45.(in Chinese))

[3]万玉珍,林德明.重塑黄土的应力-应变关系[J].岩土工程学报,1996,18(6)：106-110.(WAN Yuzhen,LIN Deming.Stressstrain relationships of remolded loess[J].Chinese Journal of Geotechnical Engineering,1996,18(6)：106-110.(in Chinese))

[4]王成华,李广信.土体应力-应变关系转型问题分析[J].岩土力学,2004,25(8)：1185-1190.(WANG Chenghua,LIGuangxin.Analysis of problem of pattern transition in stress-strain relations of soils[J].RocKand Soil Mechanics,2004,25(8)：1185-1190.(in Chinese))

[5]曾国熙.正常固结黏土不排水剪切的归一化性状[C]//南京水利科学研究院.软土地基处理学术讨论会论文选集.北京：水利出版社,1980：13-26.

[6]李作勤.黏土归一化性状的分析[J].岩土工程学报,1987,9(5)：67-75.(LI Zuoqin.Analysis of the normalized property of cohesive clay[J].Chinese Journal of Geotechnical Engineering,1987,9(5)：67-75.(in Chinese))

[7]DUNCAN JM,CHANGC Y.Nonlinear analysis of stress and strain in soils[J].Journal of the Soil Mechanics and Foundation,1970,9：1629-1654.

[8]张勇,孔令伟,孟庆山,等.武汉软土固结不排水应力-应变归一化特性分析[J].岩土力学,2006,27(9)：1509-1513.(ZHANG Yong,KONG Lingwei,MENG Qingshan,et al.Normalized stress-strain behavior of Wuhan soft clay[J].RocKand Soil Mechanics,2006,27(9)：1509-1513.(in Chinese))

[9]唐启义,冯明光.DPS数据处理系统：实验设计、统计分析及数据挖掘[M].北京：科学出版社,2007.

[10]吴简彤,王建华.神经网络技术及其应用[M].哈尔滨：哈尔滨工程大学出版社,1998.

[12]傅艳蓉.上海软土力学性质随含水量变化影响的试验研究[D].上海：同济大学,2001.