钢闸门锈蚀速率的贝叶斯更新方法

杨光明,贾文斌,陈 宁

(1.河海大学能源与电气学院,江苏南京 210098;2.河海大学可再生能源发电技术教育部工程研究中心,江苏南京 210098;3.江苏省水文水资源勘测局,江苏南京 210029)

水工金属结构设备安全评价各指标等级标准的划分主要是依据各指标的特征性状及其对设备安全影响的性态与严重程度进行[1]。平均锈蚀速率指标既是设备结构强度、刚度与稳定等安全指标复核计算的重要依据参数,也是水工金属结构综合评价的重要指标之一。锈蚀速率对水工金属结构的安全评价结果以及使用寿命估算均具有重要的影响。

当前,由于缺乏对水工金属结构锈蚀状况长期监测的历史数据与资料,因此在本行业通常把锈蚀速率看作一个确定的量,并取多年锈蚀量的平均锈蚀速率来反映金属结构的锈蚀状况。而事实上,水工金属结构处于不同时段的锈蚀状况是不同的,锈蚀速率应当是一个随着锈蚀不断发展而逐渐增大的随机变量。因此,简单地将锈蚀速率看作确定量只是对锈蚀状况的一种近似描述。

由于缺乏对水工金属结构锈蚀状况长期监测的历史数据和资料,而且工程安全评价时的实际检测数据多数为抽样检测数据,由此所得到的锈蚀速率通常存在一定的不确定性或差异性。笔者采用贝叶斯(Bayesian)理论对工程当前的锈蚀速率进行更新,减少了锈蚀速率的不确定性或差异性,使最终的评价结论更合理、更接近实际情况。同时,根据笔者在多年实际工程检测及评价工作中所积累的全国不同地区工程钢闸门锈蚀检测历史数据和资料,运用数理统计分析方法得出我国普通碳素钢在淡水中的锈蚀速率均值及其分布规律。

1 锈蚀速率的贝叶斯更新方法

钢闸门的锈蚀速率既是水工金属结构设备安全评价的重要指标,又是设备结构强度、刚度和稳定等指标的重要计算参数。因此,国内外许多学者[2-10]或从不同的角度,或采用不同的研究方法对钢闸门的锈蚀速率进行系列研究与分析,并得到许多具有实用价值的研究成果。多数研究成果表明：对工程实际检测数据采用数理统计分析方法得到的锈蚀速率不拒绝正态分布和对数正态分布,但与对数正态分布更为接近。

基于贝叶斯理论的锈蚀速率统计更新方法,就是基于工程安全评价时的实际检测锈蚀速率统计参数(即实测数据)及锈蚀速率的历史统计数据资料(即先验数据),采用贝叶斯理论对被评价工程的锈蚀速率进行统计更新。

根据各工程的历史统计数据资料,统计、分析并确定我国钢闸门锈蚀速率的频数分布及其相关的统计参数,并将其作为锈蚀速率的先验分布和统计参数。为了便于采用贝叶斯方法更新锈蚀速率的分布,一般应先按式(1)[11]对先验对数正态分布的锈蚀速率进行转化,以得到正态分布的锈蚀速率先验分布Nμ(λ0,ξ0)。

式中：μ0,σ0——先验对数正态分布的锈蚀速率均值和标准差;λ0,ξ0——先验正态分布的锈蚀速率均值和标准差。

同样,利用式(1)亦可得到被评价工程的实际检测锈蚀速率正态分布Nμ(λ,ξ)的相关统计参数。

根据被评价工程实际检测锈蚀速率的统计参数,采用贝叶斯抽样理论,由式(2)[11]可以得到正态分布的锈蚀速率后验分布Nμ(λ′,ξ′)。

式中：λ′,ξ′——后验正态分布的锈蚀速率的均值和标准差;λ,ξ——被评价工程实际检测的正态分布的锈蚀速率均值和标准差;n——统计样本的个数;σθ——被评价工程由检测不确定性所引起的标准差,一般取0.1mm/a。

由式(3)[11]可以得到被评价工程贝叶斯更新后的锈蚀速率对数正态分布Nμ(μ′,σ′)。

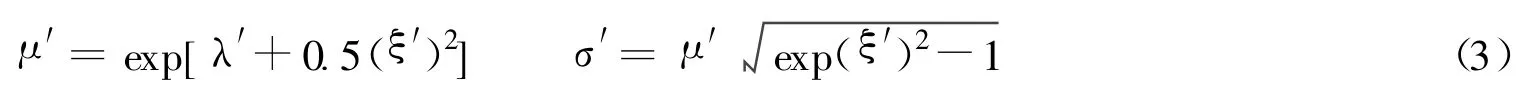
式中：μ′,σ′——被评价工程贝叶斯更新后的对数正态分布的锈蚀速率均值和标准差。

下文将通过实际工程算例来进一步证明采用贝叶斯理论更新锈蚀速率的可行性和有效性。

2 国内钢闸门锈蚀速率的统计分析

本文所用数据主要为笔者多年工作中积累的全国水利水电工程钢闸门锈蚀检测的历史数据资料及广泛收集的国内同行的历史检测数据,这些数据来自于100多座水库和水闸的200多个单位工程闸门的锈蚀速率相关数据资料。资料涉及的工程涵盖了我国不同的地域(除内蒙古以外全国所有的省、直辖市、自治区以及各流域机构),不同的闸门结构形式和规格等,因此,数据资料相对较全面,具有良好的代表性。

由于SL101—1994《水工钢闸门和启闭机安全检测技术规程》规定闸门、启闭机以及压力钢管等金属结构设备的第1次安全检测年限为5a,因此笔者将运行年限小于6a的闸门数据从所收集到的数据资料中剔除。另外,根据笔者多年的实践经验,运行年限小于6a的闸门,其防腐涂层基本完好,一般不会发生锈蚀,检测所得到的闸门锈蚀量一般是由钢材的负公差和测量误差构成。因此,闸门锈蚀量以及由此计算出的锈蚀速率并不能正确反映闸门锈蚀的真实情况,仅能反映闸门使用材料的实际厚度。而且,由于计算锈蚀速率所用的年数较小,由此所得出的闸门锈蚀速率往往会比实际的偏大,其统计结果的真实性较差。

例如：对于已运行5a而防腐涂层较好的闸门(由于防腐蚀质量问题而发生锈蚀的除外),由于钢材负公差及测量误差的存在,通常最后得到的闸门平均锈蚀量可以达到0.5mm以上,由此计算出的最小闸门锈蚀速率为0.125mm/a;而正常情况下,15a后的闸门平均锈蚀量为1.0mm左右,则锈蚀速率为0.0667mm/a。从这2组数据可以看出：闸门运行5a的锈蚀速率约为运行15a的2倍,这显然是不合理、不真实的。因此,在进行统计分析时将运行年限小于6a的闸门数据剔除,更能真实、合理地反映闸门的锈蚀性态。

对于只给出平均锈蚀速率范围的工程闸门,则采用3σ方法对其进行处理,从而可以得出锈蚀速率的均值、标准差以及变异系数。

根据上述原则,通过对收集到的历史数据资料进行统计分析计算,可以得到我国水利水电工程钢闸门锈蚀速率的频数分布及其相关的统计参数。

我国水利水电工程钢闸门锈蚀速率统计的频数分布直方图见图1,锈蚀速率的均值(μ0)、标准差(σ0)及变异系数(Cv0)分别为0.044mm/a,0.023mm/a,0.523。

由锈蚀速率统计结果、频数分布及其概率密度图(图1)可以看出：

a.我国水利水电工程钢闸门的锈蚀速率主要分布在0.016～0.055mm/a之间(其频数约为71%)。

b.依据锈蚀速率的频率分布图,分别采用正态分布和对数正态分布方法对锈蚀速率的分布状况进行模拟,可以进一步得到锈蚀速率的概率分布状况,如图1所示。按5%显著性水平采用K-S检验法[11]对锈蚀速率的2种概率分布进行检验,结果表明,锈蚀速率服从正态分布和对数正态分布,且更接近于对数正态分布。从图1亦可以看出,正态分布的部分锈蚀速率为负数,这显然是不符合实际情况的。因此,相对于正态分布,对数正态分布能更好地模拟锈蚀速率的分布情况。

据文献[12],英国、前苏联、日本的普通碳素钢在淡水中的锈蚀速率均值分别为0.05mm/a,0.015～0.05mm/a,0.031mm/a。据国内学者统计分析,我国普通碳素钢在淡水中的锈蚀速率均值一般在0.01～0.05mm/a之间[12]。

笔者统计得到的我国普通碳素钢在淡水中的锈蚀速率均值为0.044mm/a,且锈蚀速率主要分布在0.016～0.055mm/a之间。由此可以看出,国内外的普通碳素钢在淡水中的锈蚀速率基本相当,这进一步验证了笔者的统计数据资料及其结果的有效性、合理性和实用性。

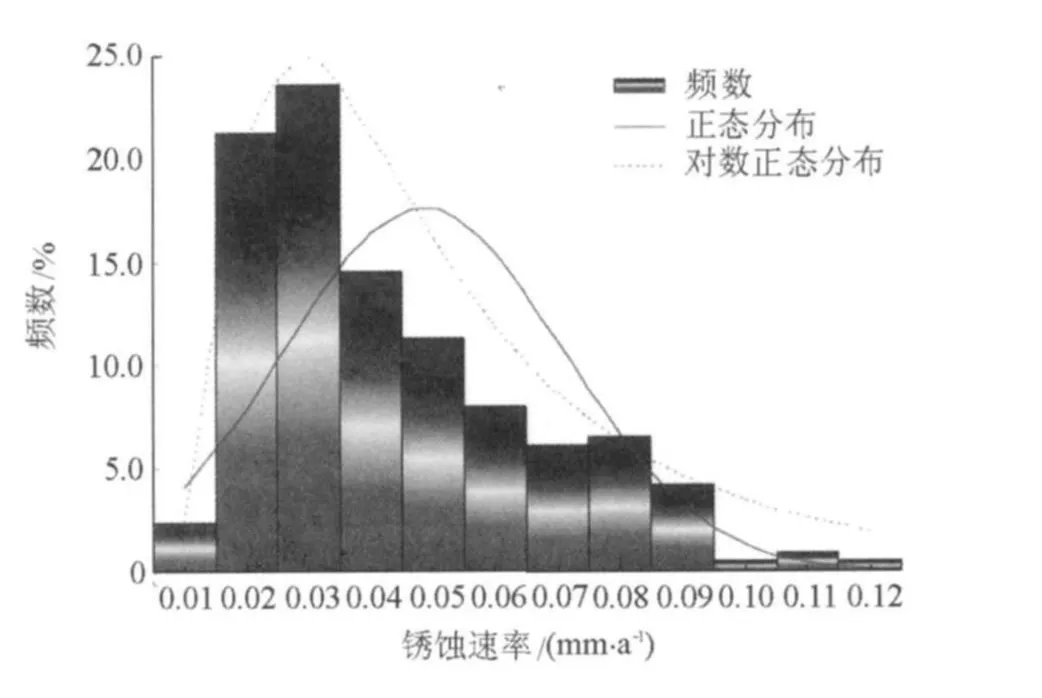
图1 锈蚀速率直方图及其概率密度Fig.1 Statistical frequency distribution and probability density of corrosion rate

3 锈蚀速率的贝叶斯更新工程算例

通过整理某水库溢洪道闸门锈蚀量检测成果,得到15组统计数据的闸门锈蚀速率均值、标准差和变异系数分别为 μ=0.061mm/a,σ=0.008mm/a,Cv=0.131。

根据式(1),得到被评价工程实测数据相应正态分布的锈蚀速率均值、标准差分别为 λ=-2.81mm/a,ξ=0.131mm/a。

根据式(1),同样可以得到先验正态分布的锈蚀速率均值和标准差分别为 λ0=-3.24 mm/a,ξ0=0.492mm/a。

根据式(2),可以计算出被评价工程实测的正态分布的锈蚀速率更新后的均值和标准差分别为 λ′=-2.83mm/a,ξ′=0.103mm/a。最后,根据式(3),可以得到更新的对数正态分布的锈蚀速率均值、标准差和变异系数分别为 μ′=0.059mm/a,σ′=0.006mm/a,Cv′=σ′/μ′=0.102。

通过采用贝叶斯理论对该工程实测锈蚀速率进行更新,可以看出,更新后的锈蚀速率均值略小于工程实际检测所得到的锈蚀速率均值;相应的变异系数明显小于先验的变异系数以及工程实际检测的变异系数。这就证明：贝叶斯理论更新方法,不仅减小了锈蚀速率的不确定性,也减少了检测数据的失真性和不确定性,是提高检测数据的准确性的一种切实可行的有效方法。

4 结 语

a.通过对笔者在多年实际工作中积累的全国水利水电工程钢闸门锈蚀检测的历史数据资料进行统计分析,得到我国普通碳素钢在淡水中的锈蚀速率均值(μ0)、标准差(σ0)及变异系数(Cv0)分别为0.044mm/a,0.023mm/a,0.523,且锈蚀速率主要分布在0.016～0.055mm/a之间。

b.工程算例中更新后的锈蚀速率均值为0.059mm/a,略小于工程实际检测所得到的锈蚀速率均值0.061mm/a,大于先验的锈蚀速率均值0.044 mm/a,这是因为检测所得到锈蚀速率均值的标准差为0.008mm/a,远小于先验锈蚀速率均值的标准差0.023mm/a。

c.工程算例中更新后的变异系数为0.102,明显小于先验的变异系数0.523,同时也小于工程实际检测的变异系数0.131。这就证明了贝叶斯理论更新方法不仅明显减小了锈蚀速率的不确定性,也减小了检测数据的失真性、不确定性,同时也是提高检测数据准确性的一种切实可行的有效方法。

致谢：本文所收集的钢闸门锈蚀速率检测历史数据资料主要为水利部水工金属结构安全监测中心全体人员在多年共同工作中所获得的现场检测资料,在此深表感谢!

[1]YANGGuangming.Research to safety evaluation expert system of hydraulic engineering metal structures[J].Applied Mechanics and Materials,2011,48/49：994-1001.

[2]PADULA JP,CHASTEN C,MLAKARP,et al.A reliability model for fatigue and corrosion of hydraulic steel structures[C]//KIM D B,ASCE M.Proceedings of the 3rd Materials Engineering Conference.Alexander：American Society of Civil Engineers,1994：1217-1224.

[3]任玉珊.既有水工钢闸门构件剩余寿命估算方法研究[J].武汉大学学报：工学版,2005,38(6)：62-65.(REN Yushan.Study on estimation of remaining life of membersof existing hydraulic steel gates[J].Engineering Journal of Wuhan University,2005,38(6)：62-65.(in Chinese))

[4]朱雅仙,朱秀娟,葛燕,等.水利水电工程中钢结构的腐蚀[J].水利水运工程学报,2002(2)：1-6.(ZHU Yaxian,ZHU Xiujuan,GEYan,et al.Corrosion of steel structures in water conservancy&hydroelectric projects[J].Hydro-Scienceand Engineering,2002(2)：1-6.(in Chinese))

[5]周建方,李典庆,李朝晖,等.钢闸门结构时变抗力模型及其可靠度分析[J].工程力学,2003,20(4)：104-109.(ZHOU Jianfang,LI Dianqing,LI Zhaohui,et al.Time-variant resistance model and reliability analysis of steel gate structures[J].Engineering Mechanics,2003,20(4)：104-109.(in Chinese))

[6]LI Dianqing,ZHOU Jianfang.Reliability assessment and acceptance criteria for existing hydraulic gates considering corrosion deterioration[J].HKIE Transactions,2007,14(2)：104-109.

[7]DAIS H,WANG M O.Reliability analysis in engineering applications[M].New York：Van Nostrand Reinhold,1992.

[8]姬永生,袁迎曙,李富民,等.混凝土内钢筋锈胀力发展及钢筋锈蚀速率的时变性[J].河海大学学报：自然科学版,2009,37(4)：430-436.(JI Yongsheng,YUAN Yingshu,LI Fumin,et al.Corrosion-induced expansive force and time-dependent change characteristics of corrosion rateof steel bars in concrete[J].Journal of Hohai University：Natural Sciences,2009,37(4)：430-436.(in Chinese))

[9]王梁英,刘华挺,张俊芝,等.人工气候环境下水工混凝土钢筋初始锈蚀时间预测[J].水利水电科技进展,2010,30(5)：9-11.(WANG Liangying,LIU Huating,ZHANG Junzhi,et al.Predictionof initial corrosion timeof steel bars in hydraulic concrete under artificial climate environment[J].Advances in Science and Technology of Water Resources,2010,30(5)：9-11.(in Chinese))

[10]朱雅仙,朱锡昶,李岩,等.大寺节制闸结构的检测与分析[J].水利水电科技进展,2007,27(3)：38-41.(ZHU Yaxian,ZHU Xichang,LIYan,et al.Inspection and analysisof concrete structures for Dasi sluice[J].Advancesin Science and Technology of Water Resources,2007,27(3)：38-41.(in Chinese))

[11]ANGH S,TANGWH.Probability concepts in engineering：emphasison applicationstocivil and environmental engineering,2nd edition[M].New York：John Wiley and Sons,2006.

[12]李典庆,吴帅兵.现役水工钢闸门锈蚀速率的统计分析[J].武汉大学学报：工学版,2007,40(2)：79-83.(LI Dianqing,WU Shuaibing.Statistical analysis of corrosion rate for existing hydraulic steel gates[J].Engineering Journal of Wuhan University,2007,40(2)：79-83.(in Chinese))