LiBr在丙酮与水的混合溶剂中溶解度的测定与关联

姜　波，李弥异，王利生

(北京理工大学化工与环境学院，北京 100081)

有关电解质溶液体系的数据对于化工分离过程的设计具有十分重要的意义，准确的溶解度数据及合适的计算模型都是必不可少的。对于电解质的相关数据，在含水体系中的溶解度数据已有很多，而在有机溶剂或水和有机溶剂的混合溶剂中的数据尚很缺乏。溴化锂作为一种高效水蒸气吸收剂和空气湿度调节剂，在制冷工业及电池工业等行业有着广泛的应用，例如：制冷工业广泛用作吸收式制冷剂，有机工业用作氯化氢脱尘剂和有机纤维膨胀剂，医药上用作催眠剂和镇静剂，电池工业用作高能电池和微型电池的电解质。此外，也用于照相行业和分析化学中。

固体溶解度数据是计算研究固-液相平衡的重要内容，是计算活度系数的基础，也是固-液相平衡理论研究的基础[1]。目前固体溶解度的理论预测和各种估算方法还不够成熟和完善，因而通过实验研究电解质在液体溶剂中的溶解度具有相当重要的意义。通过查阅大量文献及DDB数据库，确定溴化锂在不同的质量比的丙酮和水的混合溶剂中的溶解度数据还不完整。本研究选定应用广泛的溴化锂，对其在丙酮与水的混合溶剂中的溶解度进行了测定，并利用 LIFAC 模型进行了关联。

1　试验部分

1.1　试验装置与试剂

本试验中采用平衡法测定 LiBr 在丙酮和水的混合溶剂中的溶解度。

试验装置：采用如图1所示的装置测定电解质在混合溶剂中的溶解度。

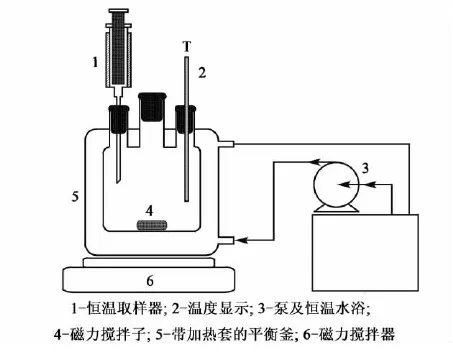
图1　溶解度测定试验装置图Fig.1　Experimental apparatus for solubility measurement

试验试剂：丙酮(分析纯，质量分数高于 99.5%)，北京北化精细化学品有限公司，没有进行二次提纯；LiBr·H2O(分析纯，质量分数高于 98.0%)，国药集团北京化学试剂有限公司，LiBr·H2O 在使用前需要180 ℃高温干燥24 h，干燥前后的 DSC 曲线及热失重曲线分别列于图2和图3中。

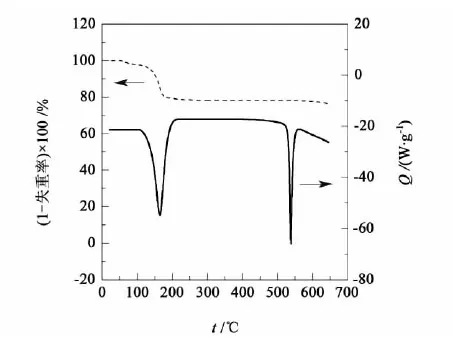
图2　LiBr·H2O干燥前的DSC曲线及热失重曲线Fig.2　DSC curve and thermo-gravimetric curve of LiBr·H2O before drying

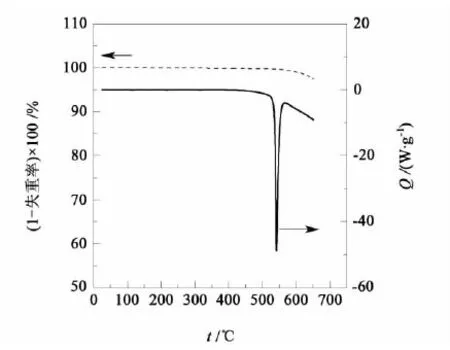
图3　LiBr·H2O干燥后的DSC曲线及热失重曲线Fig.3　DSC curve and thermo-gravimetric curve of LiBr·H2O after drying

由图2中热重曲线可见，含有1个结晶水的LiBr在160 ℃之前左右有明显质量变化，160 ℃失重达到最大值，之后趋于稳定，而与之对比的图3为干燥之后LiBr的热失重曲线中并没有出现这个质量变化，基本保持直线。此外，从图2中的DSC曲线还可知，在160 ℃有1个明显的热流变化，因而这可以证明180 ℃干燥足以使 LiBr 失去结晶水，因而在后面的溶解度测定试验中，我们将饱和溶液上清液置于180 ℃的干燥箱中烘干，可以得到LiBr。

本试验中所用设备列于表1中。

表1　溶解度测定的主要仪器设备表Table 1　Main equipment for determination of solubility

1.2　试验方法

准备好一定质量比的丙酮和水的混合溶剂，加入到平衡釜中，并加入过量的LiBr于其中，后迅速密封，搅拌同时用恒温水浴加热到指定温度，待溶质充分溶解后停止搅拌，将此过饱和溶液恒温保持4 h以上。直到溶解达到平衡，用预先加热到与溶液同温度的2 mL注射器取平衡釜中的上层清液到预先加热并称重 (m0) 的小瓶中，迅速用瓶盖住以防止灰尘进入，称重 (m1) 。 后将此小瓶放入真空干燥箱中将溶剂完全蒸发，称重 (m2) 。则溶液的质量摩尔浓度m(mol/kg) 可由式(1)计算。

(1)

其中Mm是LiBr的相对分子质量。

正式试验之前，先进行不同的溶解时间进行测试，发现10 h足够溶解达到平衡。每次取3个样本进行平行试验，溶解度取3个样本的平均值。试验中得到3次试验的最大标准误差低于2%。

2　计算模型

一个合适的能够用来计算溶剂及电解质的活度系数的热力学模型是必要的，它能可靠地解决相平衡的预测中的问题。1999年阎卫东和Gmehling等合作，把基团贡献的概念引入到LIQUAC模型[2-4]中，开发了适合混合溶剂的电解质溶液的LIFAC活度系数模型[5]，该模型在中程作用项将溶剂的相关参数分解成与UNIFAC模型相同的基团，并将UNIFAC基团相互作用参数用于中程项的参数，通过关联大量的含电解质溶液的常压相平衡数据，获得新的溶剂的基团与不同离子间的二元交互作用参数。本研究中将LIFAC模型应用于LiBr在丙酮和水中的混合电解质体系，计算活度系数，进而推算溶解度。

2.1　LIFAC模型

该模型中活度系数由3部分组成[5]。

2.1.1长程项

溶剂与离子的活度系数是表示由电荷的直接相互作用库仑力对剩余Gibbs自由能的贡献，采用Flowler-Guggenheim改进的Debye-Hückel表示。

[1+bI1/2-(1+bI1/2)-1-2ln(1+bI1/2)]

(2)

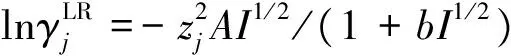
(3)

式(2)和式(3)中的A，b为Debye-Hückel常数，可由式(4)计算得出：

A=1.327 757×105d0.5/(DT)1.5

(4)

b=6.359 696d0.5/(DT)0.5

(5)

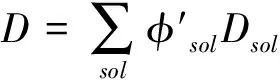
(6)

2.1.2中程项

中程项是表示的电荷之间的间接的作用力对剩余Gibbs自由能的贡献，如电荷-偶极子，诱导电荷-偶极子之间的相互作用，对于含有nkmol的溶剂基团k(k=1,2,…,s)和nj(j=1,2,…) mol离子j的溶液，

(fork=1,2,…,Nk)

(7)

式(7)中

(8)

(9)

2.1.3短程项

短程活度系数表示的是短程相互作用力对剩余 Gibbs 自由能的贡献项，可以用Fredenslund等[7]描述的 UNIFAC 基团概念来进行计算。

对于溶剂s中的任一基团k，其活度系数可由下式计算：

(10)

其中组合项与剩余项的表达式分别为：

(11)

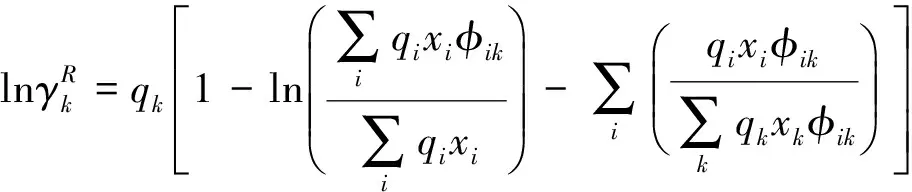
(12)

对于溶剂s，完整的活度系数表达式为：

(13)

对于盐MX平均离子活度系数为：

(14)

其中的νM与νX分别表示1 mol阳离子M和阴离子X的数量，ν=νM+νX是1 mol盐中阴阳离子的数量和。

2.2　盐在混合溶剂中溶解度的计算

有了以上电解质溶液体系活度系数的计算，就可以进一步计算出溶解度。

由于电解质在溶液中的标准吉布斯自由能等数据目前有效的仅为在纯溶剂中的一些数据，故通过一系列的转换，将电解质在混合溶剂中的标准吉布斯自由能转换为在纯水中的数据的关系式[8]为：

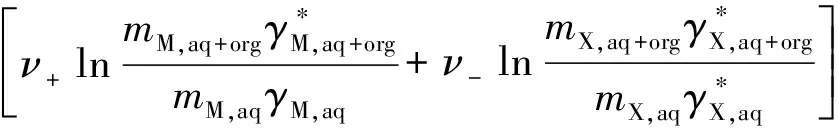
(15)

加上前面的活度系数的计算表达式，可将式(15)表示为：

[ν+ωM，aq/aq+org+ν-ωX，aq/aq+org]

(16)

其中：

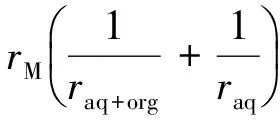
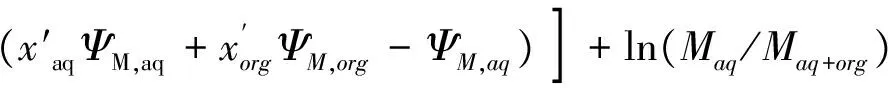
(17)

ln(Maq/Maq+org)

(18)

另由Gibbs-Helmholtz 方程，ΔGo是与温度的有关的。

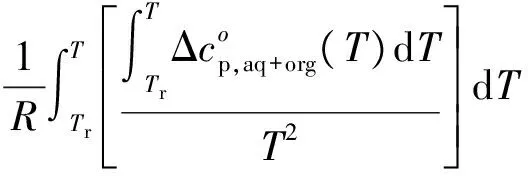
(19)

加上式(15)，可得到：

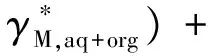
[ν+ωM,aq/aq+org+ν-ωX,aq/aq+org]

(20)

盐在含水的混合溶剂中的溶解度可以用式(20)迭代进行求解。而其中盐在含水的混合溶剂中的活度系数可以用2.1中的LIFAC模型得到。

2.3　计算结果

利用以上的活度系数模型及溶解度计算方法，我们进行了计算，所得到的计算结果与试验值的相对误差在合理的范围内。最终溶解度的试验值与计算值及相对误差列于表2中，表中w1为混合溶剂中含水的质量分数。

表2　溶解度的计算值与试验值及其相对偏差百分比Table 2　The calculated and experimental value ofsolubility and relative deviation percentage

2.4　计算偏差分析

溶解度的计算值与试验值的偏差共有3种，在计算单独样本偏差是我们用了相对偏差百分比，定义为：

(21)

计算总的计算偏差我们用了2种形式，分别为总平均相对偏差百分比和总平均绝对偏差，分别定义为：

(22)

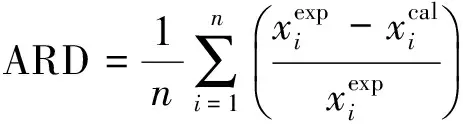
(23)

以上3种误差计算所得的值都列于表2中。

3　结果讨论

从表2中数据可以看出，LiBr 在相同质量比的丙酮和水混合溶剂中的溶解度是随着温度的升高而增大的，这与电解质在纯溶剂中的表现是一致的；而在同一温度下，随着混合溶剂中丙酮的质量百分比增加，溶解度是降低的，这表明溶剂丙酮的极性较低，在混合溶液中，对电解质的离子的吸引力没有水分子强，当丙酮的质量百分比增加时，这一规律表现的更加明显。

此外，由表2中的结果可见利用LIFAC模型得到的溶解度的计算值与试验值的总平均绝对偏差为0.054 0，总平均相对偏差为0.731 3%，这表明该模型用来计算电解质体系的活度系数，进而预测盐在混合溶剂中的溶解度是可行的。

4　结论

采用平衡法测定了LiBr在不同质量分数的丙酮与水的混合溶剂中的溶解度，并利用LIFAC模型及相关的溶解度方法进行了计算。结果表明，试验中的所有二元体系的关联结果都较好的与试验值相吻合。通过误差的分析，绝大多数二元系的误差均在1.4%以内，这表明LIFAC模型可以用来计算该电解质体系，并可以用来进一步预测溶解度数据。

符号说明：

A,b—Debye-Hückel参数；

Bij—物质i和j之间的第二维里系数；

cp—热容，J/(mol·K)；

D—介电常数；

d—密度，kg/m3；

F—vander waals表面积分数；

G—吉布斯自由能，J/mol；

I—离子强度；

H—焓 (J/mol)；

M—摩尔质量，kg/mol；

m—某一成分的质量摩尔浓度，mol/kg；

n—物质的量；

q—vander waals表面积；

R—通用气体常数，J/(mol·K)；

r—vander waals体积；

T—绝对温度，K；

V—vander waals体积分数；

x—液相摩尔分数；

y—汽相摩尔分数。

希腊字母:

φ′—液相中无盐状态下某一成分的体积分数；

φ—物质i和j之间的UNIQUAC相互作用参数;

γ—活度系数；

ν—分子中某基团数目。

上标:

C—组合项；

E—剩余项；

LR—长程；

MR—中程；

SR—短程。

下标:

a—阴离子；

c—阳离子；

i,j—组分i,j；

sol—溶剂；

ion—离子；

M—阳离子；

X—阴离子；

aq—在纯水做溶剂的溶液中的数值；

org—在纯有机溶剂的溶液中的数值；

aq+org—在水与有机溶剂混合溶液中的数值。

参考文献：

[1]胡程耀, 黄培. 固体溶解度测定方法的近期研究进展[J]. 药物分析, 2010, 30(4): 761-766

[2]LI J D, POLKA H M, GMEHLING J. AgEmodel for single and mixed solvent electrolyte systems, 1. Model and results for strong electrolytes[J]. Fluid Phase Equilib, 1994, 94: 89-114

[3]POLKA H M, LI J D, GMEHLING J. AgEmodel for single and mixed solvent electrolyte systems, 2. Results and comparision with other models[J]. Fluid Phase Equilib, 1994, 94: 115-127

[4]LI J D, LIN Y Z, GMEHLING J. AgEmodel for single and mixed solvent electrolyte systems, 3. Prediction of salt solubilities in aqueous electrolyte systems[J]. Ind Eng Chem Res, 2005, 44(5): 1 602-1 609

[5]YAN W D, TOPPHOFF M, ROSE C, GMEHLING J. Prediction of vapor-liquid equilibria in mixed-solvent electrolyte systems using the group contribution concept[J]. Fluid Phase Equilib, 1999, 162(1/2): 97-113

[6]KIEPE J, NOLL O, GMEHLING J. Modified LIQUAC and modified LIFAC-A further development of electrolyte models for the reliable prediction of phase equilibria with strong electrolytes: A group contribution method [M]. Amsterdam: Elsevier, 1977

[7]FREDENSLUND A, GMEHLING J, RASMUSSEN P. Vapor-Liquid Equilibria Using UNIFAC: A group contribution method [M]. Amsterdam: Elsevier, 1977

[8]HUANG J, LI J, GMEHLING J. Prediction of solubilities of salts, osmotic coefficients and vapor-liquid equilibria for single and mixed solvent electrolyte systems using the LIQUAC model[J]. Fluid Phase Equilib, 2009, 275(1): 8-20