一种实用的风力机叶片气动设计方法研究

昝丙合，杨旭东

（西北工业大学，翼型叶栅国家重点实验室，陕西 西安 710072）

0 引 言

风能作为环境友好型的可再生能源越来越受到人们的重视，对于风力机叶片的设计，尤其是优化设计显得越来越重要。目前存在的桨叶设计理论有Betz理论、Glauert模型、Wilson模型和儒科夫斯基模型。其中，Betz理论由于简化条件过多，因此其设计结果与实际有较大偏差。Glauert优化设计方法考虑了风轮尾流，但忽略了翼型阻力和叶尖损失的影响。Wilson理论对Glauert理论进行了修改，研究了叶尖损失与升阻比对叶片性能的影响。因此，在传统的风力机桨叶优化设计方法中，最为常用为Glauert优化设计模型以及Wilson修正模型［1］。这些方法都忽略了一些重要的问题，包括风场风况、桨叶各截面之间的约束等。所以采用这些方法设计出来的桨叶是否是最优的还值得商榷［2］。在现代叶片的优化设计过程中都要考虑风场的风速概率分布，通常采用Weibull模型［3－4］，设计目标为在满足额定功率的要求下，年能量输出最大［5－7］。本文在采用 PROPID首先对叶片确定一个较优几何外形的基础上，采用遗传算法进一步进行优化。结果发现，与原始叶片相比，风力机的年能量输出有了较大幅度的提高。

1 PROPID反设计原理

PROPID程序［8－10］是在原性能预估程序PROP［11］基础上发展而来的。PROPID程序中用于风轮性能预估的翼型数据并不唯一，不同的叶片截面可以选用不同的翼型。而且同一个截面也可以给定不同雷诺数下的翼型数据，根据雷诺数，对升力系数进行线性插值，对阻力系数进行逻辑插值。并通过普朗特损失模型、三维失速延迟模型等对二维翼型数据进行修正，以使得对风轮性能的预估更加准确。此外，PROPID最大的特点是其强大的反设计能力，它允许设计者给定风力机的性能特性，如功率峰值；或者给定叶片的气动特性，如沿叶片展向的升力系数分布进行多点反设计。PROPID程序主要是通过牛顿迭代来进行反设计。其反设计步骤如图1所示：

图1 PROPID反设计步骤Fig.1 Inverse design theory of PROPID program

其中：c0—叶片根部弦长，

Ĉ—各个站位相对于根部弦长的差值，

β0.75R—0.75半径处的扭转角，

θ—各个站位相对于0.75半径处扭转角的差值，

2 遗传算法

遗传算法（Genetic Algorithms，GA）［12－13］研究的历史比较短，20世纪60年代末到70年代初，主要由Michigan大学的John Holland等研究形成了一个比较完整的理论和方法。遗传算法由于只用编码和适应度表示问题，并不要求明确的数学方程及导数表达式，因此较之传统的优化算法通用性更强。

2.1 目标函数

将风轮扭矩M中与叶片几何外形有关的一切元素统称为g，则扭矩为：

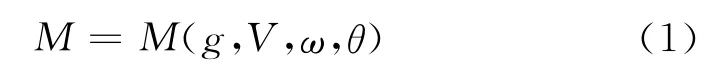
那么功率为：

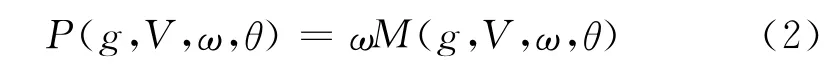
其中，ω为风轮的旋转速度。对于给定风速、转速与桨距角的情况下，功率Ρ只与叶片的几何形状有关，因此，优化过程中的目标函数定义为：

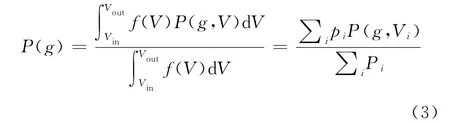
其中pi表示风速为Vi的概率。

2.2 编码控制

在优化时，选定几个截面作为控制点，控制点之间通过多项式进行插值。在控制点处给定弦长与扭转角的上下限。弦长的上限定义为cu（r），下限定义为cl（r）；同样扭转角的上限定义为ψu（r），下限定义为ψl（r）。假设种群大小为N，则半径r处的弦长与扭转角分别定义为：

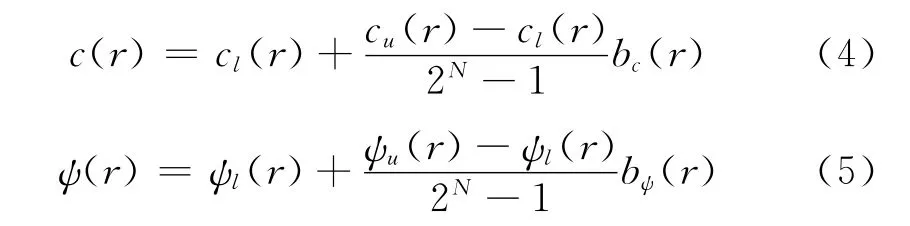
其中，bc（r），bψ（r）∈［0，2N－1］。

为了避免在种群中产生使几何形状不符合要求的个体，附加约束：

在对功率优化的程序中，如果不附加其他约束的话，弦长总是趋向于上限值。为了避免上述情况的发生，对叶片面积附加约束，在此给定叶片面积的上限，（1＋δA）A0，其中A0为叶片的初始面积。因此有叶片面积的附加约束为：

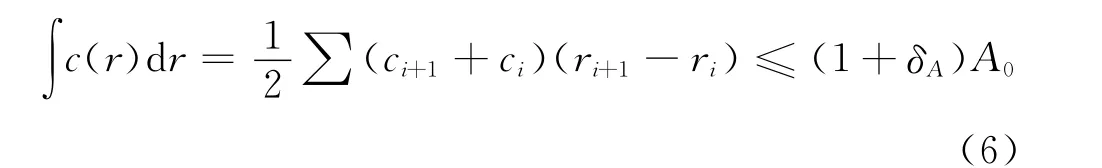
为了生成光滑的叶片几何外形，控制点之外的其他半径处的扭转角与弦长分布由5阶贝塞尔函数差值得到。

3 算例分析

3.1 验证算例

为了说明PROPID程序对风轮性能预测的准确性，选用美国国家可再生能源实验室（NREL）开发的Phase VI实验风力机叶片作为验证模型，图2为Phase VI的剖面翼型图与叶片几何外形图，整个叶片均采用S809翼型。图3为采用PROPID程序对风轮功率的预测结果。

图2 Phase VI叶片几何外形Fig.2 Blade geomtry of Phase VI

图3 RPOPID程序对Phase VI风力机性能预测结果与实验值的比较Fig.3 Comparison of the performance between the prediction of PROPID and experimental data

发现PROPID程序能够很好地对风力机性能进行预测。

3.2 采用PROPID进行反设计

本算例对某2叶片，600kW风力机叶片进行反设计，具体的设计参数如表1所示。

表1 设计风力机参数Table 1 Parameters of wind turbine

对于变速、变桨距的风力机而言，可以通过改变转速与桨距角来控制叶尖速比的大小，使其始终在功率系数最大的条件下进行工作。因此，设计目标就是使风力机的功率系数峰值最大。在本算例中，通过给定沿叶片展向的升力系数分布和周向诱导因子分布，来使得风轮功率系数峰值最大。通过平移和扭转的过程来确定最佳的分布曲线。图4为平移过程对风轮功率峰值的影响，图5为扭转过程对风轮功率峰值的影响。由于轴向诱导系数的平移与扭转扰动过程与升力系数相同，因此只画出升力系数的平移与扭转扰动关系图。

最终确定轴向诱导因子和升力系数的分布如表2所示。

图4 平移过程对功率系数峰值的影响Fig.4 Variation of CPmaxbecause of shifting of target CL／axial induction distribution

图5 扭转扰动下对功率系数峰值的影响Fig.5 Variation of CPmaxbecause of rotating of target CL／axial induction distribution

表2 轴向诱导因子与升力系数分布Table 2 Optimized CL／axial induction distribution

3.3 运用遗传算法进行优化设计

以PROPID反设计得到的叶片为基础进行优化，优化后得到的叶片几何如图6所示，从图中可以看到，在叶片根部弦长变化梯度缓和，沿叶片展向，弦长有不同程度的减小，这使得叶片的结构安全性更高。当地扭转角的分布变化平缓，有利于叶片的制造。

图7为优化前后的功率曲线对比，可以看出在风速达到12m／s之前，优化后的风轮功率优于原始风轮。

图8为原始叶片、PROPID反设计叶片以及优化后叶片的年能量输出对比。由于当风速达到12m／s时，风轮达到了额定功率600kW，因此在计算年能量输出时，只计算风速在12m／s之前的情况。在计算能量输出时风速分布采用Weibull分布，尺度参数选为8.6，形状参数选为2.66。原始风轮年能量输出为1063169kWh／年，PROPID反设计得到的风轮的年能量输出为1093854kWh／年，优化后风轮年能量输出为1126017kWh／年。比原始叶片提高了5.9114%。

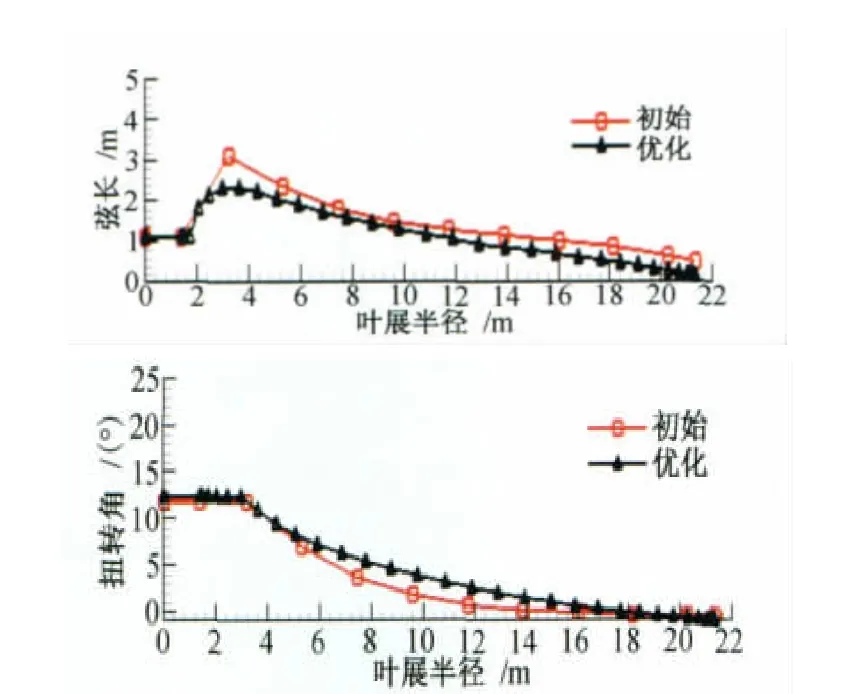
图6 优化前后几何形状对比Fig.6 Comparison of blade parameters between the optimized blade and initial blade

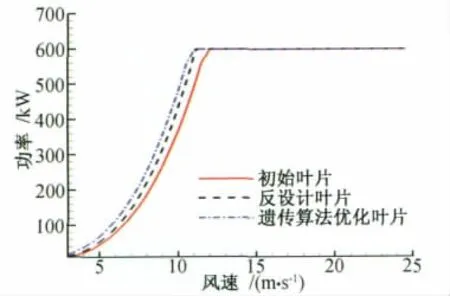
图7 优化前后功率对比Fig.7 Comparison of power between the optimized blade and initial blade

图8 优化前后年能量输出对比Fig.8 Comparison of the Annual Energy Production

4 结 论

本文提出了水平轴风力机叶片的优化设计模型，在PROPID进行反设计的基础上，采用该模型进行优化设计。以某600kW风力机为设计目标，结果发现，结合PROPID程序与该优化设计模型，能够很好地提高风力机的性能，年能量输出有了较大幅度的提高。采用5阶贝塞尔函数对控制点之间的几何进行插值获得光滑的叶片几何外形。因此，本文的优化设计方法能够高效地获得实用的高性能的风力机叶片。

［1］SPERA D A.Wind turbine technology［M］.New York：ASME Press，1994.

［2］MORGAN C A，GARRAD D.The design of optimum rotors for horizontal axis wind turbines［M］.London：Garrad Hassan and Partners，1998.

［3］DET NORSKE VERITAS，RISφNATIONAL LABORATORY.Guidelines for design of wind turbines［M］.Det Norske Veritas and RisφNational Labaratory，2002.

［4］SPERA D A.Wind turbine technology［M］.New York：ASME Press，1994.

［5］MORGAN C A，GARRAD D.The design of optimum rotors for horizontal axis wind turbines［M］.London：Garrad Hassan and Partners，1998.

［6］GIGUERE P，SELIG M S.Blade design trade－offs using low－lift airfoils for stall－regulated HAWTs［A］.Proceedings of ASME／AIAA Wind Energy Symposium［C］.Reno，Nevada Jan，1999.

［7］BENINI E，TOFFOLO A.Optimal design of horizontal－axis wind turbines using blade－element theory and evolutionary computation［J］.ASME Journal of Solar Energy Engineering，2002，124：357－363.

［8］SELIG M S，TANGLER J L.Development and application of a multipoint inverse design method for horizontal axis wind turbines［J］.Wind Engineering，1995，19（2）：91－105.

［9］GIGUERE P，SELIG M S.Aerodynamic blade design methods for horizontal axis wind turbines［A］.13thCanadian Wind Energy Association Conference and Exhibiton［C］.Quebec City，Canada，1997.

［10］SELIG M S.PROPID user manual（beta version 3.0）［M］.1998.

［11］HIBBS B，RADKEY R L.Small wind energy conversion systems（SWECS）rotor performance model comparison study［M］.Aerovironment，Inc.，Prepared for Rockwell International Corporation，1981.

［12］GOLDBERG D.Genetic algorithms in search，optimization and machine learning［M］.Addison－Wesley，1989.

［13］DAVIS L.Handbook of genetic algorithms［M］.Van Nostrand Reinhold，1991.