基于PIV技术的纵列式双旋翼尾迹特性实验研究

黄水林，林永峰，黄建萍，李 明，刘平安

（中国直升机设计研究所直升机旋翼动力学重点实验室，江西 景德镇，333001）

0 引 言

直升机旋翼尾迹几何形状随操纵和流场参数复杂多变［1］，且旋翼各桨叶的桨尖涡互诱导和自诱导作用引起的尾迹畸变使得旋翼气动特性难以准确计算。对于纵列式直升机，其旋翼尾迹中涡线之间的缠绕更为严重，两旋翼之间相互诱导作用使其气动特性比单旋翼情况更加复杂，要完全通过数值模拟来研究纵列式双旋翼气动特性是很困难的。正如文献［2］指出的那样，旋翼气动性能计算的关键是旋翼尾迹的确定，因此，深入地开展纵列式直升机双旋翼尾迹特性研究具有重要的意义。

国外基于PIV对单旋翼桨尖涡进行了不同程度的实验研究。例如，文献［3－4］采用PIV技术测量了悬停状态旋翼的桨尖涡特性，文献［5］则基于PIV技术对悬停时全尺寸和模型直升机旋翼尾迹进行了实验测量。尽管国外在这方面做了比较多的研究，但大多是针对于单旋翼直升机的悬停状态。国内在旋翼桨尖涡实验研究方面也做了一些工作，但基本是对单旋翼尾迹进行了实验测量，且主要是悬停状态。

到目前为止，国内外公开文献还没有发表过有关纵列式双旋翼情况时旋翼尾迹特性的文章。为研究双旋翼干扰对其尾迹特性的影响及与单旋翼尾迹的差异，本文基于PIV技术，在纵列式双旋翼模型实验台上，针对悬停和前飞状态下的纵列式双旋翼的桨尖涡特性进行了实验研究。测量了不同气动布局时纵列式旋翼的尾迹结构，并与单旋翼进行对比分析。本次基于PIV技术的纵列式双旋翼桨尖涡尾迹实验代表着该领域的首次尝试，目的是为纵列式双旋翼气动特性理论计算模型提供依据。

1 实验设备及模型

主要实验设备及模型有：旋翼实验台（两座）、模型桨叶及桨毂（两套）、低速风洞、PIV测量系统等。

1.1 实验台及旋翼模型

实验在南京航空航天大学直升机旋翼动力学重点实验室的2米级旋翼实验台上进行。

实验室原来的实验台（称为主旋翼台）只能用于单旋翼的实验测量，为了适合于纵列式双旋翼，本实验在实验室设备基础上增加了一个简易的旋翼实验台架（称为副旋翼台），构成了一个纵列式双旋翼模型实验系统。纵列式双旋翼实验台如图1所示。在保持转速一致的情况下，调整主旋翼台（后旋翼）的转动方向为顺时针，副旋翼台（前旋翼）的转动方向为逆时针，这样就保证了两旋翼的转速一样且旋向相反。根据风洞的吹风方向，实验时，纵列式的后旋翼置于主旋翼台上，而纵列式的前旋翼安装在副旋翼台上。

图1 纵列式双旋翼模型实验台Fig.1 Rotor model rig for tandem rotors

模型旋翼的桨毂形式是挥舞铰接式、摆振柔性片。旋转方向：后旋翼为左旋，前旋翼为右旋。转速1200r／m，对应桨尖速度约为128.177m／s。旋翼桨叶主要参数如表1所示。

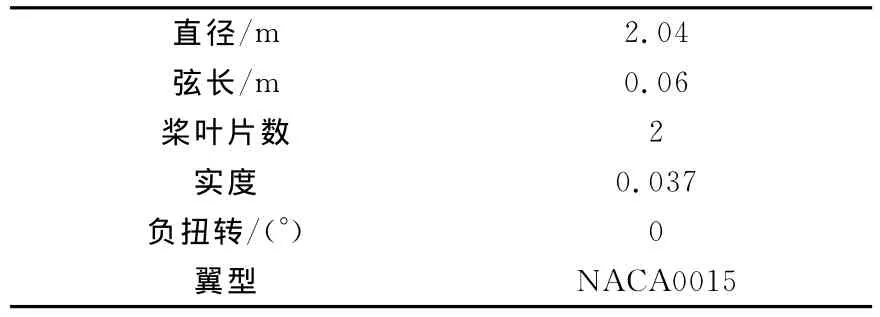
表1 旋翼桨叶主要参数Table 1 The parameters of rotor blade

1.2 旋翼流场PIV测量系统

PIV技术本质上是测量与图像分析技术的一种，它采用时间间隔很短的两个脉冲光源照亮所需要测量的流场，利用感光器（CCD）将所照明的流场中的示踪粒子记录下来，再使用计算机进行图像处理得出速度场的信息。

图2为PIV测量系统现场实物图。图2中，双脉冲激光器通过导光臂将激光引导至所需测量区域的正下方，实验测量时，发出扇形的片光，覆盖整个测量区域，再通过PIV专用相机进行拍照采样。

图2 PIV测量系统实物图Fig.2 PIV measurement system

2 实验状态及方法

旋翼尾迹测量实验的状态如表2所示。表中，dL／R代表纵向间距与旋翼半径之比，而dV／R是轴向间距与旋翼半径之比，δ表示两旋翼的重合度，φ7为总距，μ为前进比。

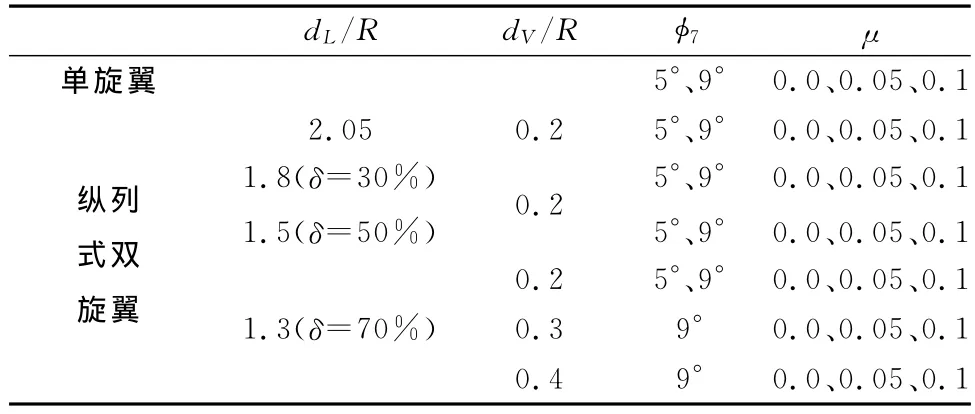
表2 旋翼尾迹测量状态Table 2 Measuring state of rotor wake

实验中通过分别调整简易旋翼台的底座高度来满足实验状态中垂向结构参数 的需要，调整简易旋翼台的纵向安装位置来改变旋翼纵向间距dL。图3是纵列式双旋翼坐标系示意图。实验时，以后旋翼的桨毂中心定义为坐标中心，沿x方向为机体纵向，沿y方向为机体横向，v代表风洞吹风方向。

图3 纵列式双旋翼坐标系示意图Fig.3 Sketch of coordinate systems for tandem twin rotors

3 实验结果及分析

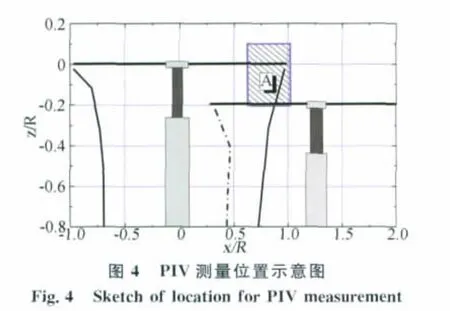
本文给出了单旋翼和双旋翼时A位置不同方位角（涡龄角）时的桨尖涡PIV测量图像。测量位置A如图4所示，A位置的测量范围为：x方向（从0.65R至1.05R），z方向（从－0.2R 至0.1R）。单旋翼情况时，只有后旋翼，没有前旋翼。为简单起见，直接用（）来代表实验时的双旋翼气动布局状态，如（1.5－0.2）表示两旋翼的纵向间距为1.5R，轴向间距为0.2R。

3.1 旋翼瞬态桨尖涡测量

图5给出了悬停状态、总距为9°时，测量的纵列式双旋翼（1.5－0.2）与单旋翼不同涡龄角时的旋翼桨尖涡位移的对比。左边一列是单旋翼桨尖涡在涡龄角（ΨW）为25.7°、77.1°、128.6°和180°时的测量图像，右边一列是这些涡龄角位置的双旋翼桨尖涡的测量图像。

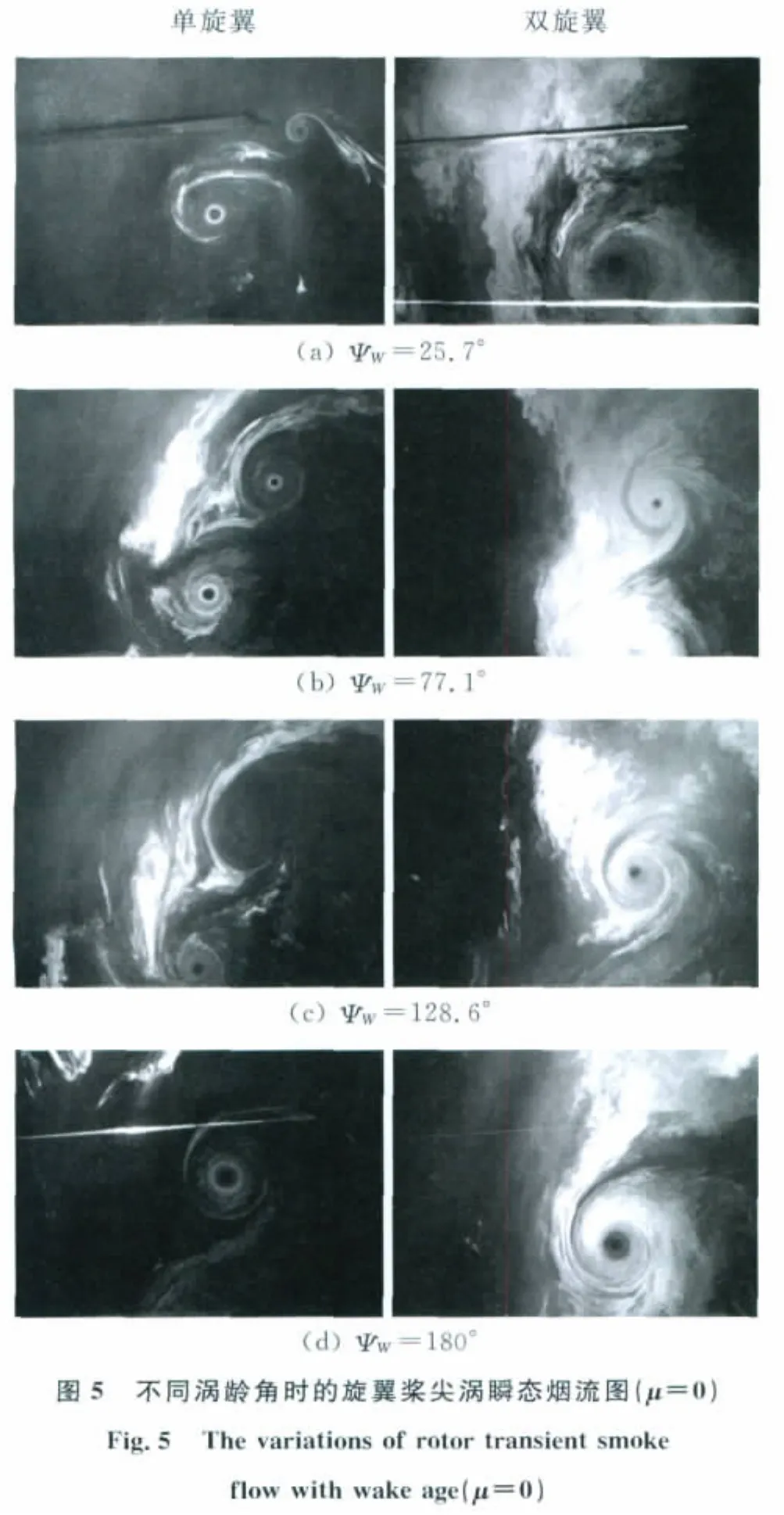
由图5可见，对于单旋翼的桨尖涡，随着涡龄角的增大，每片桨叶的桨尖涡的径向位置会越来越向里移动（图中从涡龄角25.7°、77.1°、128.6°对比可以看出）。注意，实验中的旋翼有两片桨叶，因此测量图像中包括了两个桨尖涡。图中还可看出，在涡龄角180°时，图5中测量图像对应于另外一片桨叶的桨尖涡。从桨尖涡的轴向位置对比可以看出，随着涡龄角的增大，每片桨叶的桨尖涡的轴向位置会越来越向下。这是因为悬停旋翼尾迹的轴向诱导速度所导致的，与实际［6－7］相符。

图5中也可以看出，纵列式双旋翼情况桨尖涡的径向和轴向运动变化规律与单旋翼时基本一致。与单旋翼不同的是，双旋翼时，其桨尖涡的轴向位移要大于单旋翼（图中对比左右图像的桨尖涡轴向位置），即纵列式前后旋翼的相互干扰引起尾迹的下降速度更大，而径向收缩不如单旋翼（见涡龄角为25.7°和180°时）大。

前飞时，和悬停时一样，桨尖涡在旋翼尾迹中仍然占主导地位。与悬停相比，至目前对前飞状态的旋翼尾迹的PIV实验研究进行得还不多，主要原因是因为前飞时旋翼的尾迹比悬停要复杂许多，且随流场参数变化敏感［1］。

图6是前飞状态（μ＝0.1）总距为9°时，纵列式双旋翼（1.5－0.2）与单旋翼不同方位角下的旋翼桨尖涡位移的比较，图中ΨV表示PIV对A区域的桨尖涡进行采样时桨叶所处的方位角。由图可见，对于前飞时单旋翼的桨尖涡，随着方位角的增大，每片桨叶的桨尖涡在测量的A区域的径向位置会越来越向里移动（图中ΨV从25.7°至180°对比可以看出）。图中还可看出，沿轴向，桨尖涡仍向下移动，但相对悬停时要慢。

对于纵列式双旋翼，前飞时，其桨尖涡的径向和轴向运动规律与单旋翼是类似的。但其向下的轴向运动速度都比单旋翼时更快。而径向收缩也略大于单旋翼的情况（后面的尾迹边界对比图将更清楚地示出）。

3.2 旋翼尾迹边界

本节给出了单旋翼和双旋翼不同状态、不同总距时测量的尾迹边界，并进行了对比分析。该尾迹边界通过对实验中获得的旋翼桨尖涡烟流图转化而来。

图7是悬停状态下，轴向间距0.2R、总距为9°时不同纵向间距对纵列式后旋翼桨尖涡位移影响的对比。由图可知，纵列式双旋翼时，旋翼尾迹径向收缩不如单旋翼那么严重，从图中还可以发现，纵向间距的变化对桨尖涡的运动有很大影响，尤其是径向时。而且，径向位移并不是随纵向间距的变化而规律变化，如图所示，当纵向间距为1.8时，径向收缩很小，而当纵向间距为1.3或1.5时收缩程度基本一致。这一现象可以从双旋翼重叠区域的尾迹边界来解释，当纵向间距为1.8R附近时，后（上）旋翼的尾迹边界刚好处于下旋翼桨尖附近，此时会产生一个类似于双旋翼横列式排列时的有利干扰［8］。由图7（b）可以看出，纵向间距对轴向位移具有一定影响，且随两旋翼纵向间距的增大，桨尖涡的轴向位移越来越大。

图8是悬停状态下，纵向间距1.3R、总距为9°时不同轴向间距对纵列式后旋翼桨尖涡位移影响的对比。由图可知，双旋翼时，轴向间距的变化对径向和轴向位移具有一些影响，但都不是很大。

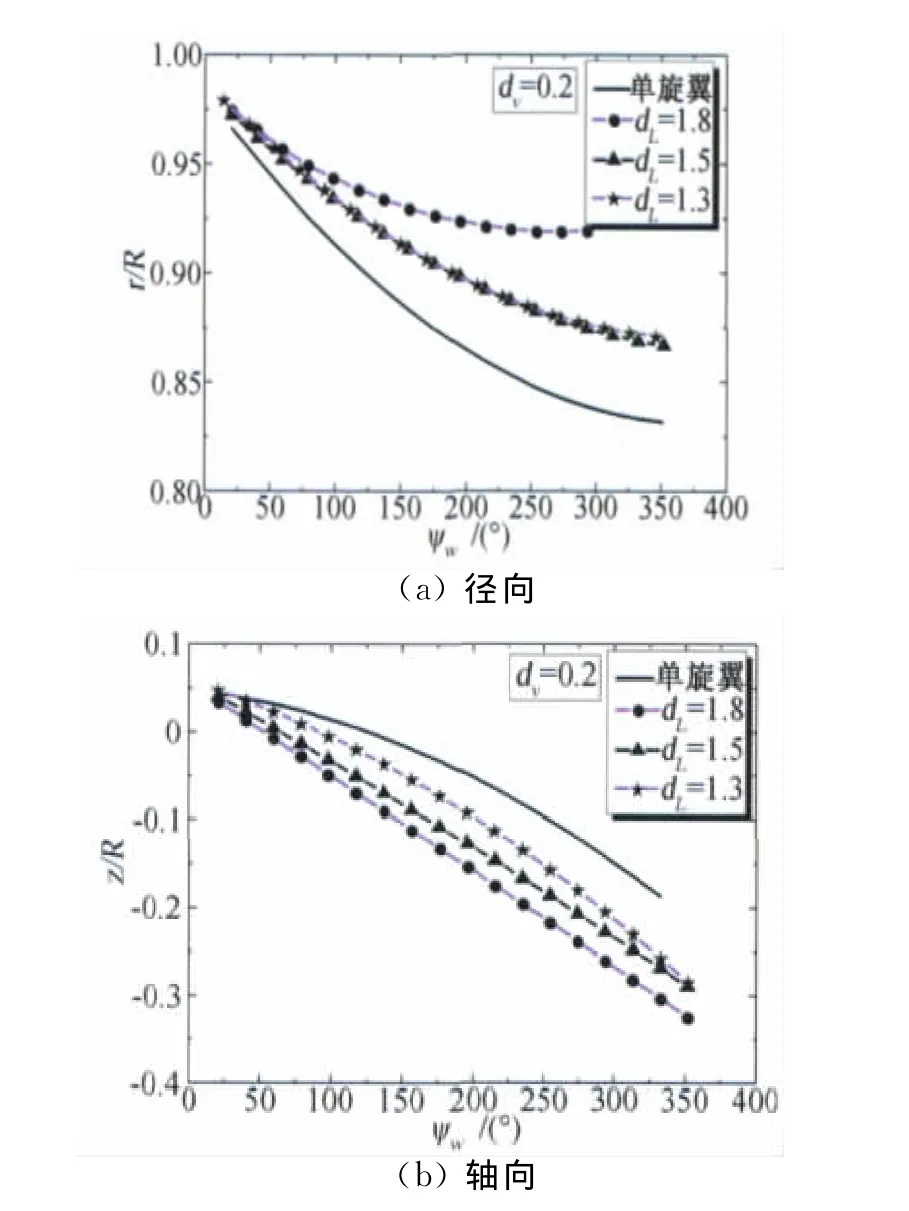
图7 不同纵向间距时后旋翼桨尖涡位移随涡龄角的变化（φ7＝9°，μ＝0）Fig.7 The displacement of aft rotor blade tip vortices with wake age in different longitudinal distances（φ7＝9°，μ＝0）

图8 不同轴向间距时后旋翼桨尖涡位移随涡龄角的变化（φ7＝9°，μ＝0）Fig.8 The displacement of aft rotor blade tip vortices with wake age in different axial distances（φ7＝9°，μ＝0）

图9为不同纵向间距时旋翼桨尖涡位移随方位角的变化。图中对应的轴向间距为0.2R，前进比μ＝0.1，总距为9°。由图可见，前飞状态下，双旋翼时的桨尖涡径向收缩比单旋翼时要更大些，这与前飞尾迹的偏斜有关。而桨尖涡轴向位移比单旋翼时要大。

图9 不同纵向间距时旋翼桨尖涡位移随方位角的变化（φ7＝9°，μ＝0.1）Fig.9 The displacement of aft rotor blade tip vortices with wake age in different longitudinal distances（φ7＝9°，μ＝0.1）

图10给出的是纵向间距1.3R、总距9°，不同轴向间距时的旋翼桨尖涡位移随方位角的变化。对应的前进比为μ＝0.1。可见，不同轴向间距对纵列式旋翼的桨尖涡位移有一定的影响，且在方位角大时影响更为明显。

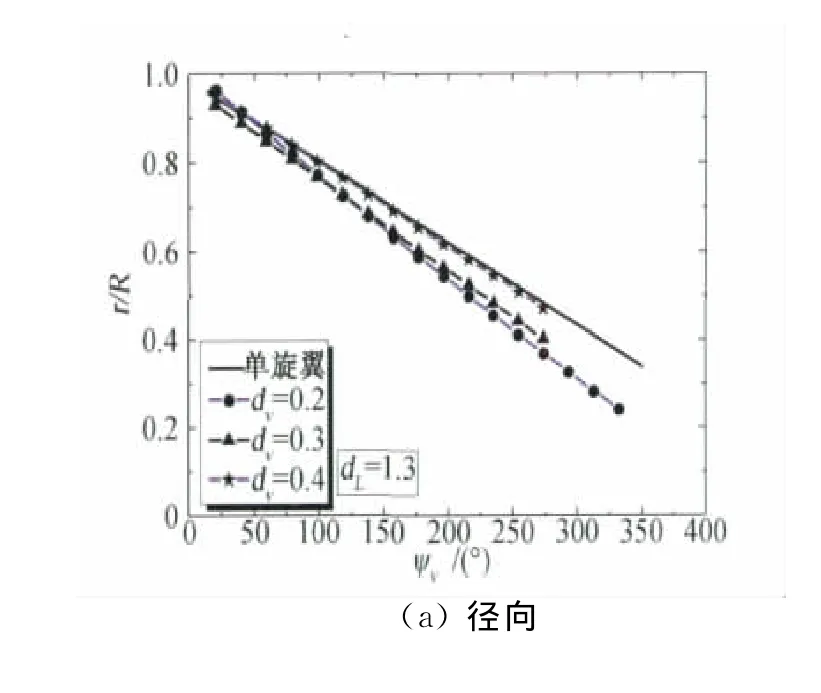
图10 不同轴向间距时旋翼桨尖涡位移随方位角的变化（φ7＝9°，μ＝0.1）Fig.10 The displacement of aft rotor blade tip vortices with wake age in different axial distances（φ7＝9°，μ＝0.1）

4 结 论

（1）悬停状态，无论是纵列式双旋翼还是单旋翼情况，随着涡龄角的增大，桨尖涡的径向位置都会越来越向里移动，轴向运动越来越向下。双旋翼时桨尖涡的轴向位移要大于单旋翼，但径向收缩不如单旋翼明显。

（2）前飞时单旋翼的桨尖涡随着方位角的增大，径向位置会越来越向里移动，沿轴向仍向下移动，但相对悬停时要慢。双旋翼情况时，其向下的轴向运动速度都比单旋翼时更快，径向收缩也略大于单旋翼的情况。

（3）悬停状态，桨尖涡轴向位移随两旋翼纵向间距的增加而不断增大，但径向位移并不是随纵向间距的变化而规律变化，在纵向间距为1.8R附近时最小；轴向间距的变化对桨尖涡的径向和轴向位移都有影响，但变化都不是很大。

（4）前飞时不同气动布局对纵列式旋翼的桨尖涡位移有一定的影响，且在方位角大时影响更为明显。

［1］BHAGWAT M J，LEISHMAN J G.Stability analysis of helicopter rotor wakes in axial flight［J］.Journal of the American Helicopter Society，2000，45（2）：165－178.

［2］LORBER P F，STAUTER R C，LANDGREBE A J.A Comprehensive hover test of the airloads and airflow of an extensively instrumented model helicopter rotor［A］.Proceedings of the American Helicopter Society 45th Annual Forum［C］.1989.

［3］MARTIN P B，PUGLIESE G J，LEISHMAN J G.Stereoscopic PIV measurements in the wake of a hovering rotor［A］.Proceedings of the American Helicopter Society 56th Annual Forum［C］.2000.

［4］HEINECK J T，YAMAUCHI G K，WADCOCK A J，et al.Application of three－component piv to a hovering rotor wake［A］.56th Annual National Forum of the A－merican Helicopter Society［C］.Virginia Beach，VA，2000.

［5］RICHARD H，RAFFEL M.Rotor wake measurements：fullscale and model tests［A］.Proceedings of the American Helicopter Society 58th Annual Forum［C］.2002.

［6］JOHNSON W.Helicopter theory［M］.Princeton University Press，1980.

［7］LEISHMAN J G.Principles of helicopter aerodynamics［M］.New York：Cambridge University Press，2000.

［8］郭才根，郭士龙.直升机总体设计［M］.航空工业出版社，1993.