基于数值模拟的复杂地形风场风资源评估方法

梁思超，张晓东，康 顺，2，康雅兰，赵永锋

（1.华北电力大学电站设备状态监测与控制教育部重点实验室，北京 102206；2.西安现代控制技术研究所，陕西 西安 710065；3.中国电力工程顾问集团华北电力设计院工程有限公司，北京 100120；4.中国福霖风能工程有限公司，北京 100034）

0 引 言

风电场风资源评估和微观选址的好坏将直接关系到风电场发电量的多少。经过大量工程实践，基于线性模型的WAsP软件被认为不适用于复杂地形风场。计算流体力学（CFD）作为一种很有前途的手段，在这一领域正不断发展。

湍流数值模拟方法主要有直接模拟（DNS）、大涡模拟（LES）、分离涡模拟（DES）以及雷诺时均模拟（RANS）。从精度上看，在实际山地Bolund山测风实验的盲评中，排名靠前的均为两方程的雷诺时均数值模拟方法，优于大涡模拟和风洞实验结果。综合计算精度，运算时间，计算机资源，雷诺时均法还没有受到其他任何模拟方法的挑战［1］。

带有壁面函数的k－ε湍流模型，由于同时考虑了风速，湍动能以及地表粗糙度，适于风工程的研究。为把这一用于工业流动问题的模型用于风工程研究，前人对湍流模型参数进行了修正［2－3］。2009 年 在NUMECA软件平台下，提出其他相关参数对模拟的影响，作出进一步修正［4］。使用该修正模型的Askervein山数值模拟结果很好地与实验值吻合。

为了将这一模拟方法用于实际风场的风资源评估和微观选址中去，以实际南澳岛风场为研究对象。结合测绘数据和卫星数据等间隔生成不同风向下的计算域，进行全周数值模拟。

1 南澳岛简介

为了简化问题，降低边界条件设置难度，选取岛屿地形南澳岛风场作为研究对象。南澳岛濒临台湾海峡，处于南海北部，距离汕头市莱芜岛约10km，面积106.45km2，岛上山地面积占93.6%。岛上平均风速达8.44m／s，年有效发电小时数达7215h，年平均有效风能密度为678W／m2，有东北和西南两个主风向，风力资源居世界最佳之列。

图1 南澳岛Fig.1 Nanao island

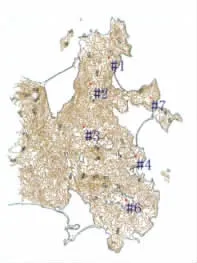
图2 固定测风塔位置Fig.2 Fixed masts positions

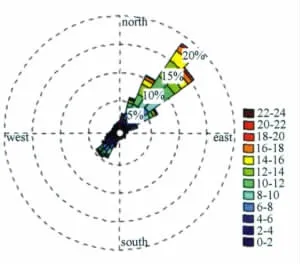
图3 6号塔风向玫瑰图Fig.3 Wind rose of 6＃

南澳风电场资源勘测期间，设立了若干固定测风塔和移动测风塔。其中，1、2、3、4、6、7号测风塔为固定测风塔，测有全年风资源数据，位置如图2所示。从6号测风塔70m高度处风向玫瑰图（图3）中可以看到，南澳岛的主风向为40°左右。

2 数值方法

采用NUMECA的FINE／TURBO软件包，该软件采用时间相关法求解湍流Navier－Stokes方程、中心节点的有限体积离散、显式Runge－Kutta法，全多重网格初场处理以及多重网格迭代加速收敛。选用的湍流模型为带有壁面函数的k－ε湍流模型。

2.1 k－ε两方程湍流模型

标准k－ε湍流模型三维标准输送方程为：

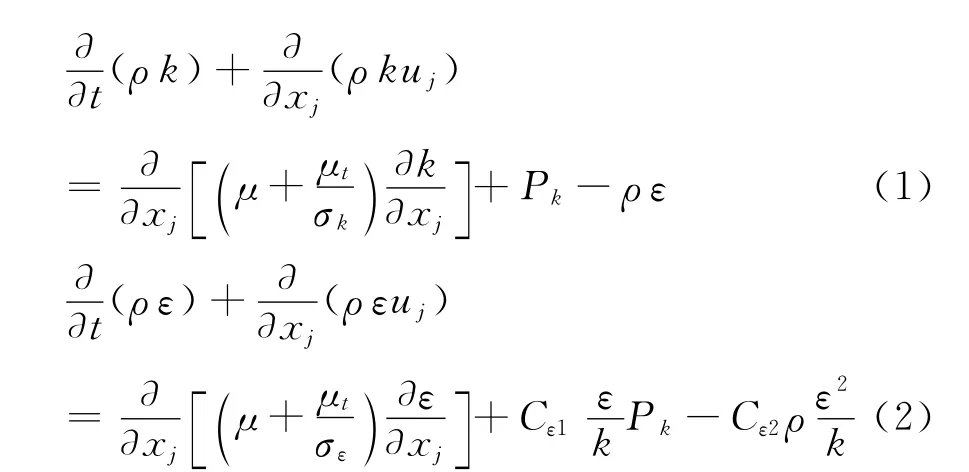
k和ε为湍动能及耗散率，湍动能生成项Pk为：

式（3）中，uj和分别为j方向的平均风速和脉动速度。湍流粘度为：

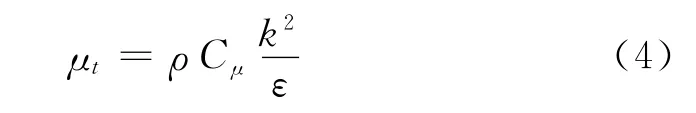
湍流模型参数参数Cμ、Cε1、Cε2、σk、σε在模拟大气边界层时设置为Cμ＝0.03，Cε1＝1.21，Cε2＝1.92，σk＝1.0，σε＝1.3［5］。为排除软件对流场中μtx／μ的影响，设置 MUCLIP＝1×109。

数值迭代时，由于湍动能是从入口不断向出口发展的，迭代速度很慢，不利于计算的收敛。将参数KEGRID的值设置为大于全多重网格加速重数的最大值。此时，湍动能k会在最粗网格上进行迭代，为较细网格的迭代提供好的初场，加速收敛，防止发散。计算中KEGRID取4。

2.2 壁面函数

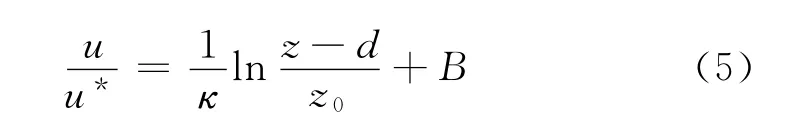
在FINE／TURBO软件中，不考虑粘性底层的存在，粗糙度z0为粗糙地表上风速为零点到粗糙地表顶端的距离。壁面函数的表达式如下：其中，u＊为摩擦速度，与壁面剪切应力τwall有关，u＊卡门常数κ一般取0.41。z0为表面粗糙度，d为零偏移量，定义u（z0＋d）＝0。当d≠0时，相当于把壁面移到距真实壁面距离d 的地方。对于粗糙壁时，常数B取零。其中，ksy＋／y，y＋＝yu＊／v。计算中取d＝0，B＝0。

3 计算域与边界条件设置

实际风工程中，由于经费有限，只测绘风场内有限的地形区域。而在CFD中，为了考虑周围地形对风场空气流动的影响，需要更大区域的地形数据来生成计算域和网格。针对这一问题，提出结合网上可免费获取的SRTM卫星地形数据，补全测绘地形数据的方案。卫星数据绝对水平和高程精度分别为20m和16m，仅作为地形补充，精度足够。南澳岛风场二期的测绘地形数据与卫星数据如图4、图5所示。地形处理时考虑了WGS84与北京54坐标的转换、二维插值、两地形间的平滑［5］。

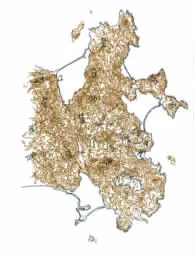
图4 测绘地形图Fig.4 Mapping terrain data

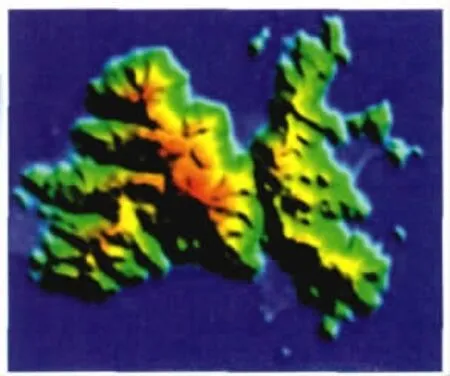
图5 SRTM卫星地形图Fig.5 SRTM terrain data

以30°为间隔，分别进行12个风向的数值模拟。图6为0°、30°、60°风向下的计算域和网格。由于风向正交，如0°、90°、180°、270°，这四个风向采用相同的计算域和网格。于是，模拟中仅需要三个计算域，根据风向设置相应的边界条件（即风速的大小和方向）即可。另做40°主风向计算域，这样就有4个不同的计算域。

图6 风向角为0°、30°、60°的网格和计算域Fig.6 Grids and domains of 0°，30°and 60°degree

计算域尺寸为18000m×18000m×4000m。水平方向网格单元尺寸为90m×90m。计算域x、y、z三个方向的网格数为200、200、76。垂直方向网格分布分为三层结构：底层、中层和顶层（图7）。底层网格共高10m，共有3个网格单元，按等延展比分布，第一层网格高度2.3m。中层内每个网格高度相等，均为5m，共12个。顶层网格也按等延展比分布，随着高度的增加网格单元尺度增大。由于中层和底层内每个网格单元具有固定的高度，在后处理时，可以在一定高度上生成一个与地面起伏趋势相同的网格面，便于分析模拟结果。

以40°风向计算为例（图8），设置边界条件时，来流方向边界为入口边界，对面一侧为出口边界，两侧为镜像边界，计算域顶端为入口边界，地面为粗糙固壁。将计算域划分为若干块，便于在不同固壁区域设置不同的地表粗糙度。设置海面粗糙度为0.002m，陆地粗糙度为0.3m。

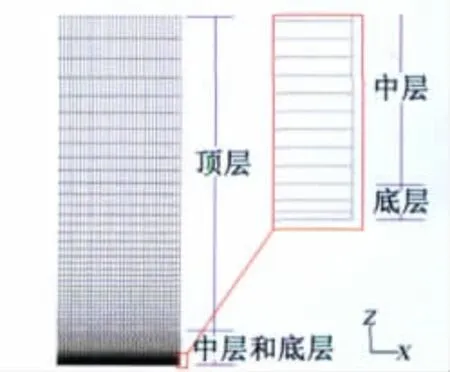
图7 垂直方向网格分布Fig.7 Vertical grid distribution

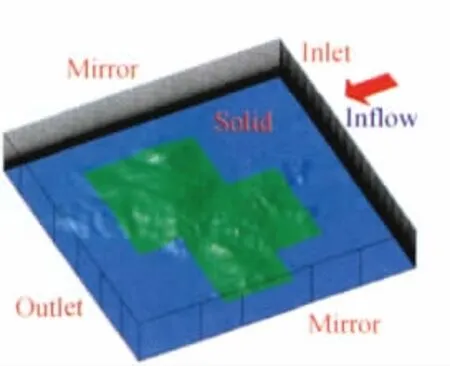
图8 边界条件设置 Fig.8 Boundary conditions

入口边界上速度、湍动能、以及耗散率由以下模型确定［6］。

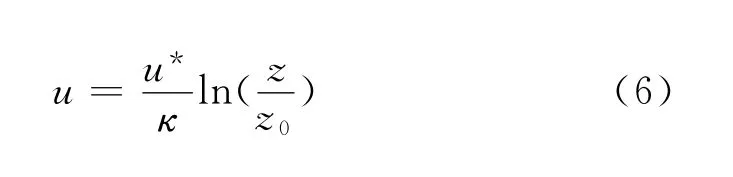
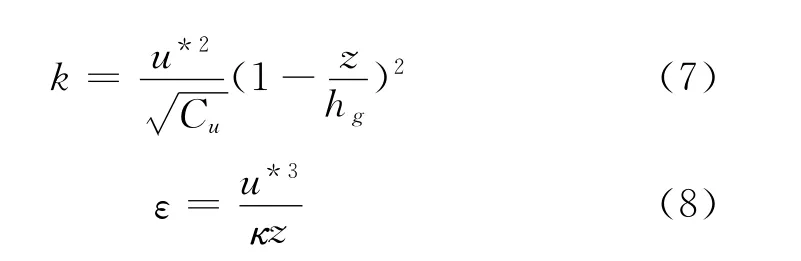
其中，κ取0.4，Cu＝0.03。hg为大气边界层高度，hg＝u＊／6f，f为科里奥利参数，f＝2Ωsin a（｜λ｜），其中，Ω为地球自转的角速度，λ为风场所处纬度位置。认为大气边界层顶端为湍动能消失的地方，当高度超过大气边界层高度时，速度不再变化，湍动能和耗散率为零。计算中，Ω＝7.292×10－5rad，λ取23.5°，z0取0.002m。以50m为特征高度，以风速2、4、6、8、10、12、14、16、18、20m／s作为特征值，根据式（6）分别计算u＊，生成来流条件。

4 模拟结果分析

4.1 不同来流条件对计算结果的影响

为了研究不同来流风速对于模拟结果的影响，引入无量纲量风加速ΔS，定义式为：

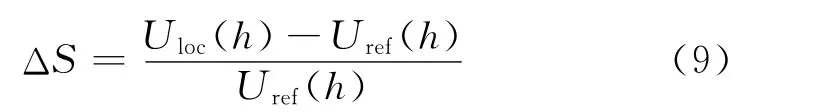
Uloc（h）为距地表高h处的当地风速，Uref（h）为参考风速。取50m高处的风速进行比较。各向同性时，湍流强度IT与湍动能k和风速U的关系为：

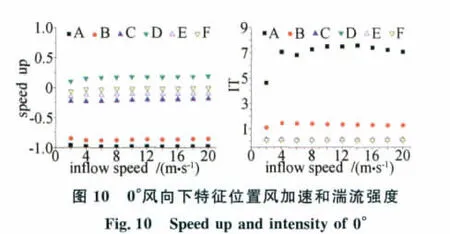
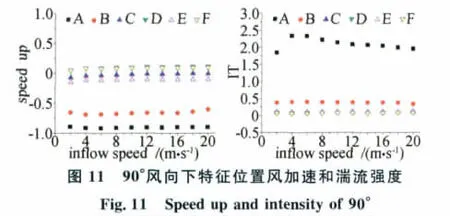
以0°和90°风向计算为例，分别选取6个位置（如图9）。其中，A点和B点位于背风坡；C点和D点位于山顶；E点和F点位于迎风坡。图10和图11分别为各个位置50m高度上的风加速和湍流强度与入口特征风速的关系。虽然各点位置不同，流动状况也不同，但所处位置上的风加速和湍流强度基本上不随来流发生变化，其余风向模拟结果均存在这一规律。这对于后处理带来了极大的方便，每个方向仅作一个风况的特征计算即可。

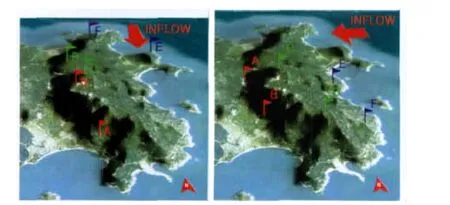
图9 0°和90°风向下特征位置Fig.9 Characteristic positions of 0°and 90°

4.2 计算结果比较

由于以上规律的存在，可以认为：同风向下、不同风速时，风场不同位置两处风速比例关系不变。因此，在一个风向下，当知道某一位置的风速U1时，可采用公式（11）计算另一位置风速U2。其中，Us1和Us2为该风向下，对应位置模拟值。

为验证数值模拟的精度，进行各测风塔间的风速互相推算比较。除6号塔外，其余各塔1、2、3、4、7均有50m高度处的数据。以7号塔风向为风向基准，在风向和风速稳定的时间段内选取3个小时平均数据，见表1。由式（11），以各测风塔风速计算其它测风塔位置处风速，并比较差异，得到表2～表4。

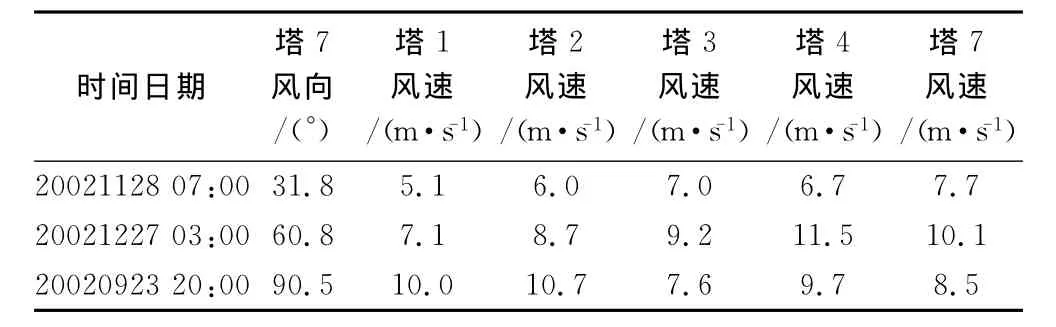
表1 样本风速Table 1 Sample wind speed data

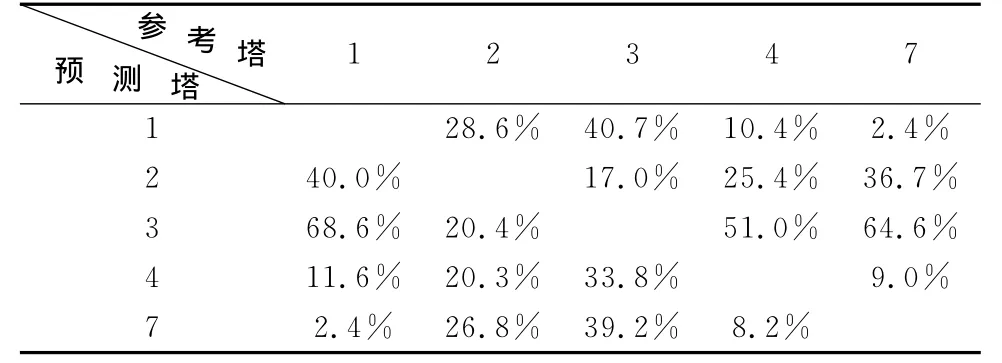
表2 30°风向计算结果比较Table 2 30°results comparisons

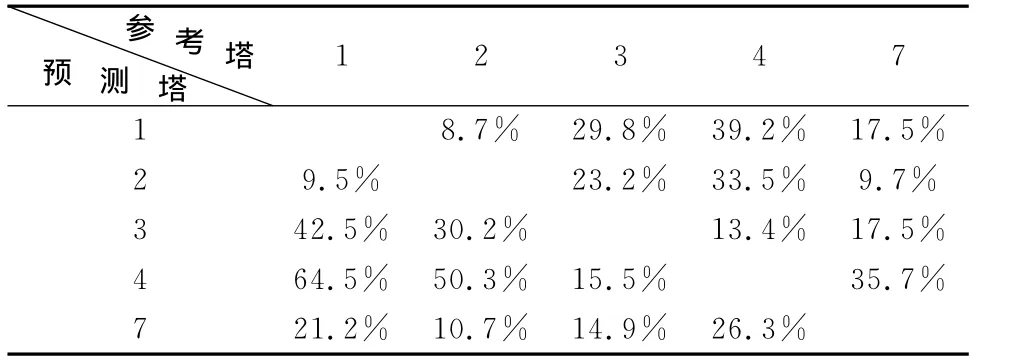
表3 60°风向计算结果比较Table 3 60°results comparisons

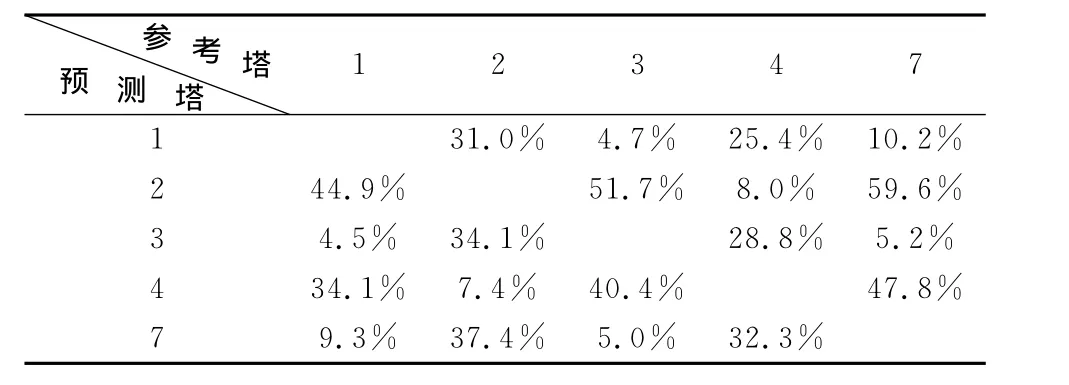
表4 90°风向计算结果比较Table 4 90°results comparisons

从三个风向的互推差异来看（表2、表3、表4），数值模拟结果存在较大误差。产生误差的原因可能来自两方面。一是数值模拟网格的太稀，不能很好地表现地面的起伏状况，简单的壁面函数不足以描述复杂的粗糙地表。二是由于安装，损坏，附近障碍物影响等原因造成的测量数据不准。但无论怎样，这一方法在风资源评估当中是值得借鉴的。

4.3 主风向下的流场分析及微观选址

由于40°为该风场的主风向，研究该风向下的流场分布状况是十分必要的。图12中标出的7个位置，综合空气流动状况，风能密度和湍流强度，适于安装风力机。最下面的区域由于面积较大，地形平坦，便于施工，应优先考虑。

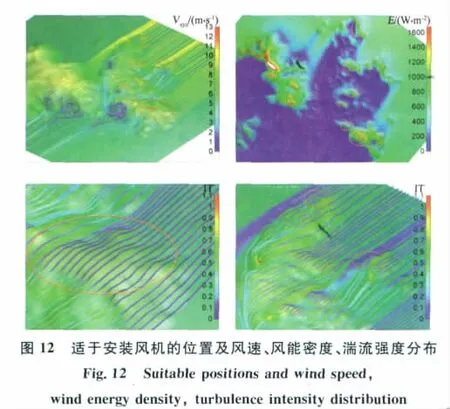
风场区域内有4个位置（图13）处于背风处，流动状况复杂，风能密度小，流动不平稳。尤其是最下那个区域，处于高山的背风坡，十分陡峭，又由于左侧山地的阻挡作用，一股气流斜向流入，加剧了该处的流动分离。这些位置的湍流强度明显大于周围，因此，要避免在这些位置安装风力机。

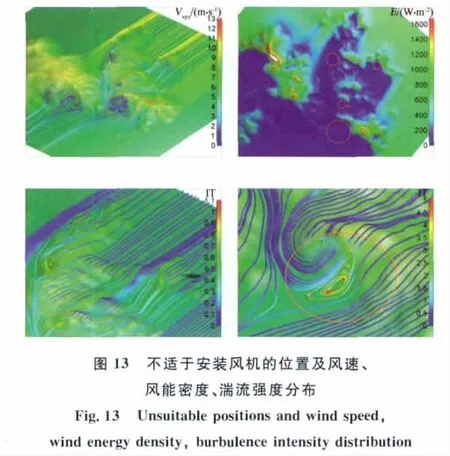
5 全周模拟结果的后处理

实际工程当中，为了简化计算，多采用威布尔分布来拟合测风数据，描述风速的概率分布。但很多情况下，风速概率分布不满足威布尔分布。这时，可采用处理时间序列的方式来评估风资源。即，每一个测风数据均进行累计计算。

处理时，选择一位于高处、受地形影响较小的测风塔作为基准测风塔，用来判定该时刻的风况属于哪个风向的数值计算。在风场区域内布置二维网格面，利用式（11）计算节点i采用第j个测风塔的数据点得到的风速Uij。由于测风塔往往有n个，可采用反距离加权法计算该结点的风速Ui，即：

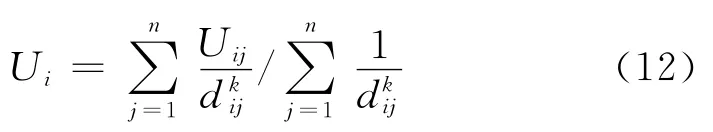
其中dij为节点i到测风塔j的距离。用每一时刻测风数据计算得到风能密度，累计相加后平均，即得到每个网格点上的年平均风能密度。得到风场区域年平均风能密度云图，如图14。

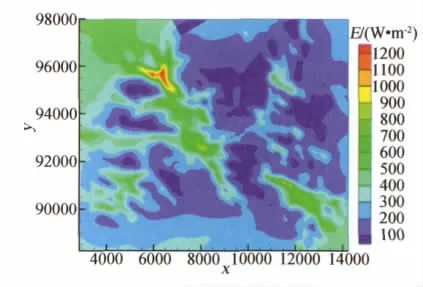
图1 4 年平均风能密度云图Fig.1 4 Annual average wind energy density contour

6 结 论

在相同计算域下，地表附近风加速和湍流强度模拟值基本上不随入口参考风速的变化而发生变化。因此，当知道风场某一位置的风速和湍流强度时，可根据模拟值计算出另一位置的风速和湍流强度。基于这一思想，建立起的数值模拟和后处理方法对于实际风场的风资源评估具有积极的指导作用。

［1］HANJALIC K，KENJERES S.Some developments in turbulence modeling for wind and environmental engineering［J］.Journal of Wind Engineering and Industrial Aerodynamics，2008，96（10－11）：1537－1570.

［2］BECHMANN A，SORENSEN N N，JOHNSEN S，et al.Hybrid RANS／LES method for high Reynolds numbers，applied to atmospheric flow over complex terrain［A］.The Science of Making Torque from Wind［C］.Lyngby，DENMARK，2007.No.012054.

［3］YANG Y，GU M，CHEN S Q，et al.New inflow boundary conditions for modelling the neutral equilibrium atmospheric boundary layer in computational wind engineering［J］.J.of Wind Engineering and Industrial Aerodynamics，2009，97：88－95.

［4］梁思超，张晓东，康顺.复杂地形风场扰流数值模拟方法［J］.工程热物理学报，2011，32（6）：945－948.

［5］梁思超.复杂地形风场数值处理及扰流模拟方法研［D］.［硕士论文］.北京：华北电力大学，2010.

［6］ZHANG X D.CFD simulation of neutral ABL flows［R］.Risø－R－1688（EN），2009.