基于近海海面观测的台风黑格比风特性研究

肖仪清，李利孝，宋丽莉，秦 鹏

（1.哈尔滨工业大学深圳研究生院，广东 深圳 518055；2.广东省气候与农业气象中心，广东 广州 510080）

0 引 言

随着我国国民经济的发展，城市土地资源匮乏及城市品牌效益的追求，建筑结构向着高、轻、柔的方向发展，导致结构的风敏感性增加，风荷载成为这类结构的控制荷载。尤其在台风影响区已建或即将兴建的大量高层建筑，如上海中心、深圳京基大厦、平安银行大厦、广州东西双塔、广州电视塔等，抵抗台风作用成为这些结构设计的关键所在。而在过去的几十年，由于人类对自然环境的过度破坏，导致灾害性天气的强度和频度也在近几年逐渐增加，尤其是每年的破坏性台风频繁发生［1］。

建筑结构设计可分为荷载估算和抗力设计两个步骤。对于台风影响区的风敏感结构，如何准确地估计结构上的台风荷载作用及作用形式成为这类结构设计的重中之重。为了准确刻画在台风影响区结构的台风荷载，国内外专家学者进行了大量风特性和结构风效应现场实测研究，如 Xu［2］，Choi［3］和黄世成［4］等，但是由于台风本身机理的复杂性、发生的相对稀缺性以及观测的困难性，到目前为止这方面相对成熟的成果还较少。同时台风是水汽交换作用的结果，其风场特性对地形地貌的影响非常敏感，已进行的台风风场特性的观测研究基本上是在沿海地区或内陆相对平坦场地进行的，很难反映台风风场本身的特性，在海面上进行观测研究成果非常少，只有Sparks［5－6］和Harper［7］进行了少量的海面观测研究。本文针对在博贺海洋观测站上测得的0814强台风黑格比，研究了其在海面上的风场特性，给出了风场特性参数，并与海岸观测结果［8］进行了对比分析，为进一步研究台风登陆后衰减过程中风场特性提供借鉴。

1 博贺海洋观测站介绍

博贺海洋观测站位于广东省茂名市电白县博贺镇至沙扒镇之间对开海面约3km处的峙仔岛上。峙仔岛是一个距离陆地约4km的无人岛，小岛长120m，宽50m，最高海拔只有11m，周围海水深6m～10m，非常适合开展海陆气相互作用试验。在峙仔岛上东经111°22′28.02″E，北纬21°27′3.12″N，海拔11m 高度处建了一座高度为100m的观测铁塔，在塔身离地8m高度处安装了美国NRG公司的气温计和气压计，在离地10、20、40、60、80、100m 高度处安装了风速仪，在10、60、100m高度处安装了风向仪，测风仪全部为美国NRG Symphonie型测风仪，在60m高度安装了GillWindMasterPro超声风速仪进行脉动风场测量。铁塔及风速仪安装图如图1（a）所示。在观测塔的正南侧1.14km处有一个最高海拔高度为48m的大竹洲岛；在观测塔的东北偏北侧距离12km为沙扒镇；在观测站正西侧6.5km和正北侧6.0km及之间均为内陆地区，最短距离为4.4km，其他侧均为外海面。详细地形情况如图1（b）所示。沙角旋海岸观测塔的详细地形情况以及风速仪安装见参考文献［8］。

图1 观测站仪器设置及地形图Fig.1 Instruments setting of station and topographic map

2 台风黑格比介绍

台风黑格比是2008年的第14号强台风，也是至1996年以来登陆广东的最强台风。黑格比于9月19日早上在香港东南偏东约2540km的北太平洋西部海上形成，并向西南偏西移动，它于9月24日早上6时45分在广东西部电白陈村附近登陆，登陆时中心风力达15级（48m／s），图2给出了台风黑格比的路径图。

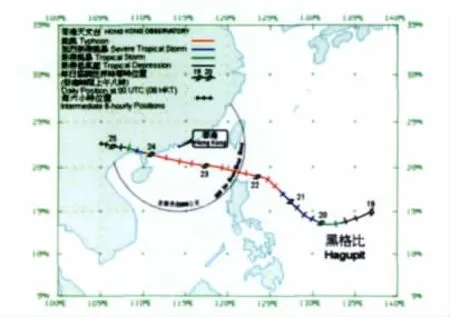
图2 台风黑格比路径图Fig.2 Track of typhoon Hagupit

3 数据质量控制方法和样本选取原则

在台风条件下，常伴有强降雨，并且在空气中有时会夹杂一些风致飞射物，以及台风导致电压不稳和环境噪声等使得采用超声风速仪进行台风现场实测时，观测到的数据中总是存在坏点和野点。另外，在实际观测中还常存在如下几类无以避免的误差［9］：（1）实测中缺乏真正各向同性的场地以及恒定粗糙度的实验条件；（2）不存在完全中性的大气层结条件；（3）不同的信号处理技术以及湍流参数的计算方法产生的误差；（4）湍流本身的随机性。所有这些误差最终都将影响台风条件下平均和脉动风特性的计算及反演。

综合分析各类误差来源以及特征，可将其划分为如下三类：（1）显著误差，这类误差主要由于强降雨或风致飞射物的干扰，电压的不稳定性造成的，基本上用肉眼就能识别出来，通常称为野点；（2）趋势误差，这类误差主要由于在测试中采样频率的限制，以及与电源频率重合产生“折叠效应”，测试时长没有经历所有大涡运动的特性等导致的；（3）随机误差，这类误差主要是由于试验条件和湍流信号本身的随机性导致。

针对以上实测数据误差，许多文献提出了不同的处理方法，如李鹏飞采用的“子样本分割法”［10］、孙建超采用的“绝对均值法”［11］等，但是都没有系统的对数据样本进行检测处理，本文根据对大量实测台风数据的分析经验，提出如下系统的数据检测处理方法：

（1）首先根据风速仪自带的判别码，判别出坏点，采用五点三次插值法进行替换；

（2）绘制风速时程，找出其中的野点，采用五点三次插值法进行替换；

（3）进行子样本分割，根据需要分割为长度为L（通常为10min）的子样本；

（4）针对后两类误差导致的不合理点，采用一个长度为L1（通常为1min或30s）的矩形窗以一个数据为单位进行滑移，然后计算每一个矩形窗的均值和标准差，如果某个值与均值差的绝对值大于3.5倍标准差，则认为其为不合理点，采用五点三次插值法进行替换，这个过程一直重复，直到没有不合理点检测出来为止，在第二次检测时标准差倍数取为3.6，当不合理点数量超过总点数的1%，认为数据样本不合理；

（5）大气湍流谱分析理论建立在自然界风过程是平稳各态遍历的随机过程的假定基础上，而实测台风过程中风时程具有非平稳和非高斯特性，因此在计算湍流参数时，应尽可能地减少非平稳特性的影响，需进行去除趋势项处理；

（6）对子样本进行平稳性检验，检测数据合理性。

通过上述数据质量控制之后，样本可以进行风特性研究及谱分析研究。

当计算湍流参数时，同一风速时程的不同样本计算结果离散性较大，故如何判定台风特性及选取样本进行台风风特性研究至关重要，本文采取如下原则：

（1）平均风速标准，当气旋中心风力小于6级时，将不具有螺旋结构，对流发展较差，不能反映台风特性。根据世界气象组织的规定，8级及以上的风力，即底层中心最大平均风速大于17.2m／s时，具有一定的破坏力，同时只有当风速较大时才能满足近似中性层结假定，故在研究台风特性时，样本10分钟平均风速应大于17.2m／s；

（2）平均风向标准，台风风眼前后眼壁区风向存在约180°相角差，距离风眼越远，风向相对转角越小。而台风的强风、高湍流度、螺旋及剖面特征均发生在眼壁强风区，外围与常态大风特性类似。故所选样本拟反映眼壁强风区风特性，需台风中心经过观测站前后样本10min平均风向相对转变应大于90°；

（3）样本风向标准，不同的下垫面强烈影响风特性，上风向风区长度的变化导致内边界层风场高度改变，外边界层的风场特征受上风向下垫面的影响［12］。因此所选样本的上风向粗糙度长度不能发生较大的变化，故选取样本时样本内瞬时风向变化应小于22.5°。

4 风场特性分析

本文分析了2008年9月24日00：00时到次日00：00时在博贺海洋观测站得到的数据，数据长24h。平均风剖面数据为每10min输出一次平均值。脉动风场研究所采用的数据为60m高度安装的Gill WindMaster Pro超声风速仪观测到的数据，采样频率为10Hz。

4.1 平均风速、风向、风攻角

Gill WindMaster Pro超声风速仪输出的为三个方向的风速矢量 ，通过风轴坐标转换求得平均风速、风向、风攻角和脉动风速。

根据实测数据，以10min为基本时距的平均风速、风向和风攻角如图3所示，10分钟平均风速的最大值为45.88m／s。在9月24日早上6时台风正中心经过观测站，在中心经过前后风向角有一个大约192°的转变。风攻角介于－1°～7°之间。在眼壁强风区和风眼区，全部为正攻角，介于1°～7°之间。当台风后眼壁经过后，攻角急剧下降，基本上介于－1°～2°。在眼壁强风区有较大的正攻角，由台风风场导致的攻角大约为3～7°，大于规范［13］规定的－3°～3°之间。

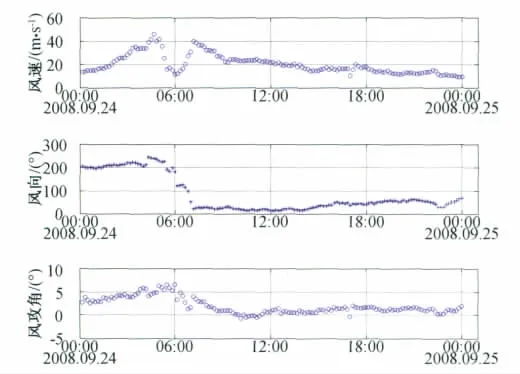
图3 十分钟平均风速、风向和风攻角随时间变化历程Fig.3 Wind speed direction and attack angle varying history

4.2 风剖面

风剖面描述了平均风速随高度的变化规律，台风条件下，由于台风的强对流作用以及台风本身结构特性，导致台风与常态风剖面不同。常用的风速剖面模型有：

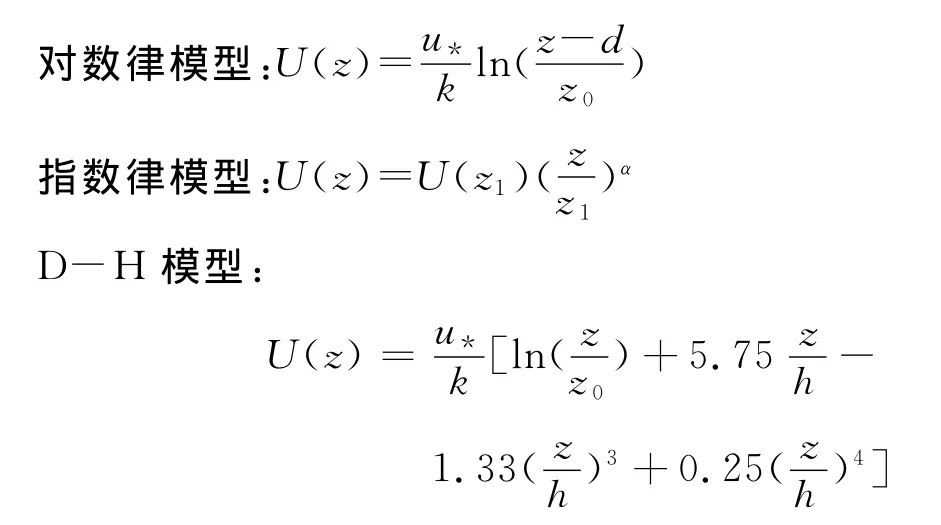
其中d为零平面位移，u＊为摩擦速度，h为大气边界层高度，z0为粗糙度长度，k为卡门常数。

本文根据在观测站所测到的梯度风场数据，得到了台风前眼壁强风区、风眼区和后眼壁强风区风剖面如图4所示，由于在近地100m风剖面与对数率剖面符合较差，故只给出了A类场地的指数律剖面。由图4可见，无论是眼壁区还是风眼区剖面均比A类场地指数律剖面陡，指数a远小于A类场地类别规范推荐值。图5给出了风剖面随时间的变化历程，从图上我们可以发现在台风前眼壁强风区，在近地面（10m高度）有一个近地急流层，随着台风中心区经过之后，该急流层的高度逐渐移动到40m左右。采用指数律拟合的台风眼壁强风区和风眼区风剖面指数如表1所列，同时给出了沙角旋海岸观测塔的结果作为对比，在海面下垫面时，指数a小于规范推荐的A类场地类别相应值。

表1 指数律风剖面指数aTable 1 Exponential index a in power law

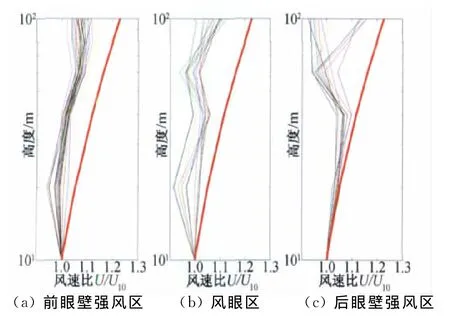
图4 台风不同部位风剖面与指数律比较Fig.4 Wind profile and exponential law in different parts

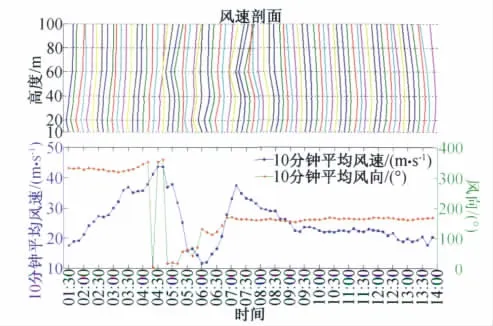
图5 台风黑格比风剖面发展历程Fig.5 Wind profile varying history

4.3 梯度风高度

梯度风高度表征了大气边界层的厚度，在梯度风高度以上大气运动将不再受地面摩擦的影响。Deaves和Harris［14］给出了下式来计算梯度风高度：

其中u＊为摩阻速度，fc为科里奥利参数。根据在观测站60m高度超声风速仪实测所得到的数据，用公式（1）计算了梯度风高度如图6所示，梯度风高度的最大值出现在十分钟平均风速最大值附近，略微提前。风场前眼壁强风区梯度风高度平均值为3368.7m，风场后眼壁强风区梯度风高度平均值为2692.4m。Franklin等［15］发现台风风速沿高度有多个局部极大值，平均梯度风高度大约在离地500m高度左右，远小于公式（1）计算结果，可能是因为在台风条件下对流湍流比重增加，梯度风高度不再单纯地由机械湍流控制。

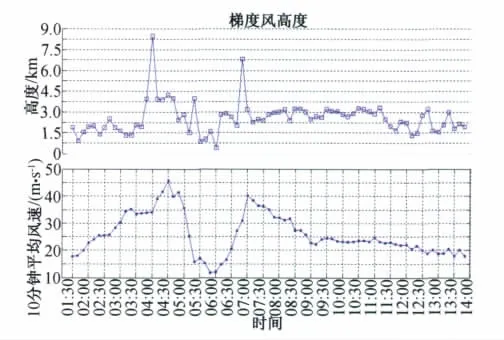
图6 梯度风高度随风场变化特征Fig.6 Gradient wind height varying history

4.4 阵风因子与湍流强度

阵风因子是不同时距平均风速转换的关系，也是我国《建筑结构荷载规范》［16］风荷载中围护结构抗风设计的重要参数。本文选取3s阵风持时研究了阵风因子与平均风速的关系如图7所示，发现在海面观测的阵风因子随着平均风速的增大而增大，当平均风速大于30m／s时，基本上不再变化。在图7同时对比了沙角旋海岸观测塔11m高度超声风速仪的结果，当平均风速较大（大于17.2m／s）时，阵风因子基本上不发生变化，可能是在海面上，随着风速的增加，浪高增加而导致粗糙度增加，当在风速达到一定值之后，在海面形成一个新的平衡层，粗糙度相对稳定，湍流参数将不再发生变化。实测阵风因子列于表2。

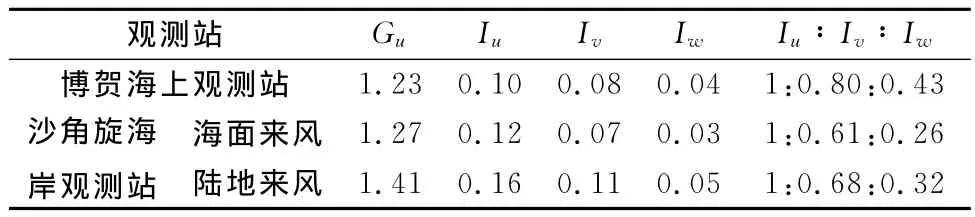
表2 阵风因子和湍流强度Table 2 Gust factor and turbulence intensity

湍流强度表征了风的脉动程度。图8给出了博贺海上观测站湍流强度随平均风速的变化关系，同时给出了沙角旋海岸观测站结果进行对比。当风速大于17.2m／s时，湍流强度基本上不随平均风速变化。博贺站三个方向湍流强度的比值与我国规范给出的1∶0.88∶0.52相对较为接近，而沙角旋海岸观测结果有较大差异，可能是因为观测高度在11m，受地形影响较多。实测不同地形三向湍流强度的对比列于表2。

Ishizaki［17］和 Choi［18］建议的湍流强度和阵风因子之间的关系，可统一用下式表示：

Ishizaki建议k1＝0.5，k2＝1.0，Choi建议k1＝0.62，k2＝1.7。图9给出了湍流强度与阵风因子的变换关系，从图9可见湍流强度与阵风因子的变换关系不是完全线性的。Ishizaki所建议的参数在台风黑格比博贺海上观测站观测结果中高估了二者之间的关系，而Choi所建议的参数低估了二者之间的关系，根据实测结果拟合得到两个参数分别为k1＝0.48，k2＝1.04。

图7 阵风因子随平均风速变化关系Fig.7 Relationship between gust factor and mean wind speed

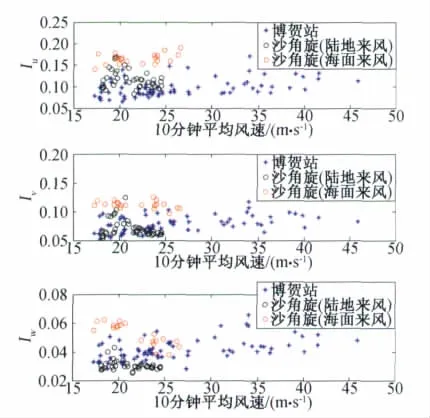
图8 湍流强度随平均风速变化关系Fig.8 Relationship between turbulence intensity and speed

4.5 时间尺度和积分长度尺度

通常假定自然界风为水平平稳气流，因此自相关函数仅与离地高度和时间差τ有关。时间尺度用来描述时间轴上两点脉动风速的相关情况。我们认为时间差τ≪T（z）时，两脉动风矢量具有较大的相关性，反之亦然。时间尺度定义为：

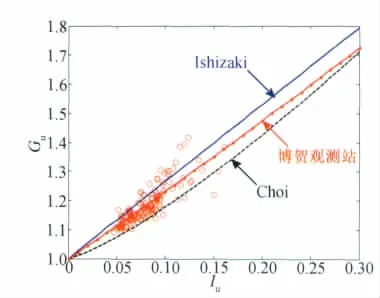
图9 阵风因子随湍流强度变化关系Fig.9 Ralationship between gust factor and intensity

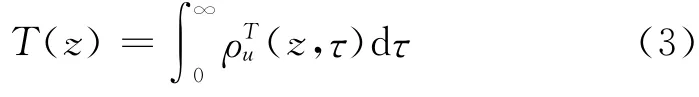
积分长度尺度是湍流中漩涡平均尺度的度量。用来描述空间两点脉动风速的相关情况。积分长度尺度在数学上可以定义为：

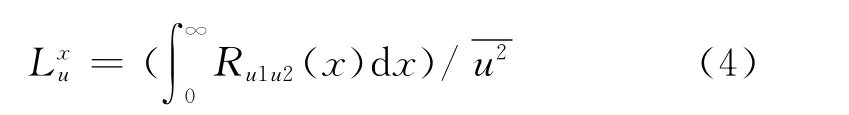
根据泰勒的“凝固湍流”假设，空间两点脉动可转换为时间轴上相应两点的脉动。于是积分长度尺度和时间尺度具有如下关系：

图10给出了博贺海上观测站实测样本的时间尺度随时间发展的历程，由图我们发现风眼区时间尺度较大，在眼壁强风区最大风速位置略微提前一点出现了较大的时间尺度。在强风区时间尺度基本上小于30s，与台风中湍流的特征尺度一致。竖向时间尺度均小于10s，表明竖向湍流相关性较弱。图11给出了积分尺度随风场发展的变化关系，我们可以发现与时间尺度类似变化规律，最大值均出现在眼壁强风区，但是比风速最大值出现略微提前一点。在前眼壁强风区纵向、横向和竖向积分尺度的平均值分别为466m、441m和111m；后眼壁强风区三个方向的积分尺度平均值分别为460.84m、401m和85m。由此可见在海面上受局部地形的影响较小，纵向和横向湍流相当，只有在竖直方向上湍流较小。当平均风速大于17.2m／s以后，湍流积分尺度随平均风速的变化没有固定的规律。表3列出了博贺观测站和沙角旋观测塔观测结果，下垫面为海面时积分尺度远大于陆地下垫面的结果。在沙角旋海面来风时，由于眼壁区风向发生急变，横风向样本出现非平稳性，导致横风向积分尺度大于顺风向值。

4.6 脉动风速谱

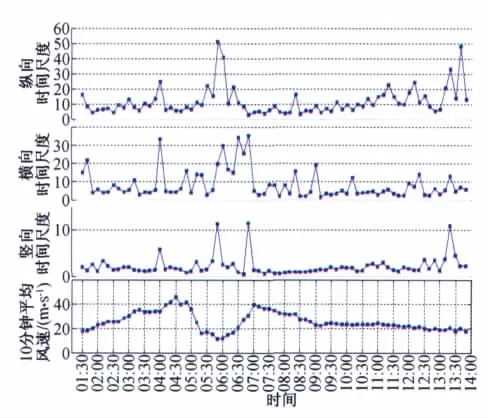
图10 时间尺度随风场发展的变化关系Fig.10 Time scale varying history

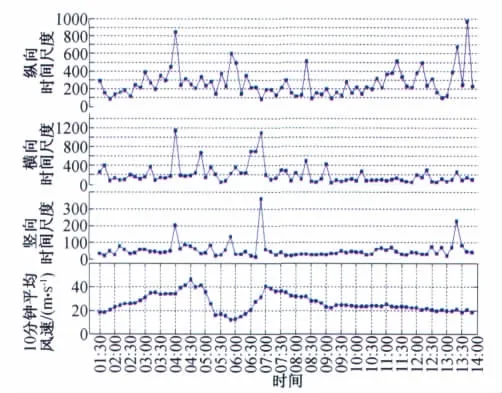
图11 积分尺度随风场发展的变化关系Fig.11 Integral scale varying history

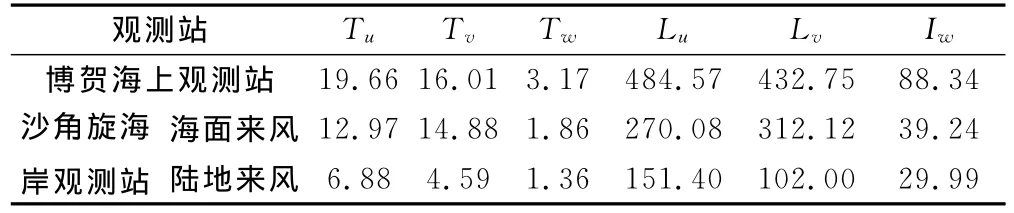
表3 积分时间尺度和积分长度尺度Table 3 Integral time scale and length scale

脉动风速谱表征了湍动能在不同频率（漩涡）上的分布。脉动风速谱是结构抗风设计至关重要的一个参量，基于Kolmogorov假设，大量学者根据实测资料研究了脉动风速谱的表达式，如von Karman谱、Davenport谱、Kaimal谱、Panofsky谱等，以及对各脉动风速谱进行修正，如Solari［19］、Tieleman［20］等，但是真正针对台风特性的风速谱特性研究还较少。尽管各风速谱的表达形式各不相同，根据Tieleman［20］建议，风速谱可统一表示为：其中A、B、C、α、β和γ为六个待定参数，满足γ－αβ＝－2／3。

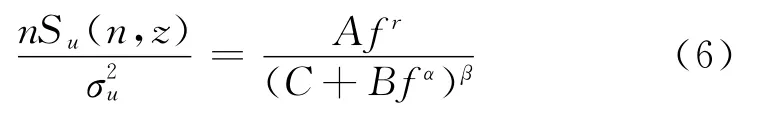
本文根据实测数据，选取了前、后眼壁强风区和外风场三个时间段各一小时的时程样本研究了台风不同部位风速谱特性。前眼壁强风区10分钟平均风速介于35.66～45.88m／s，平均值为40.61m／s，风向介于223°～244°之间，积分长度尺度平均值为259m；后眼壁强风区10分钟平均风速介于32.30～40.07m／s之间，平均值为36.44m／s，风向介于20°～28°之间，积分长度尺度平均值为180m；外风场10分钟平均风速介于16.18～20.49m／s之间，平均值为18.05m／s，风向介于40°～47°之间，积分长度尺度平均值为149m。图12给出了所选取样本的示意图。

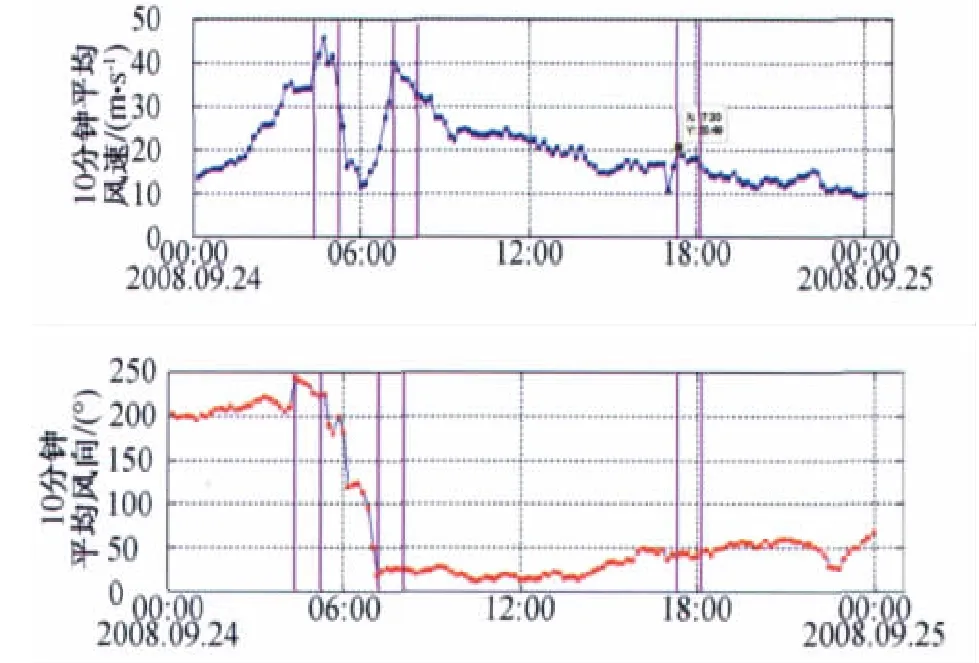
图12 风速谱分析样本Fig.12 Specimen used for analyzing wind spectra

图13给出了三个样本的实测风速谱，同时给出了经验谱：von Karman谱、Davenport谱和Kaimal谱对比。从图13我们可以发现，在双对数坐标系中，前眼壁强风区的峰值频率为0.0232Hz，无量纲化峰值能量为0.3215；后眼壁强风区的峰值频率为0.0427Hz，无量纲化峰值能量为0.2698；外风场区的峰值频率为0.0208Hz，无量纲化峰值能量为0.2706。

前眼壁强风区风速谱，von Karman谱在低频区（＜0.02Hz）略微高估了风速谱能量，对峰值频率的估计比较准确，无量纲化峰值能量为0.2713；在土木工程结构通常所关心的高频区（＞0.1Hz），von Karman谱和Kaimal谱则低估了谱能量，Davenport谱在高频区高估了谱能量，实测谱在高频区基本上介于Kaimal谱和Davenport谱之间。后眼壁强风区风速谱，von Karman谱同样在低频区略微高估了风速谱能量，对峰值频率的估计值为0.0300Hz，低于实测值，可能因为实测样本的湍流积分尺度估计值略微偏高导致峰值频率的估计稍微偏小，对无量纲化峰值能量估计较为接近；在高频区，同样von Karman谱低估了风谱能量，实测风谱在高频区介于von Karman谱和Davenport之间。对外风场区风速谱，von Karman谱亦在低频区略微高估了风速谱能量，对峰值频率的估计值为0.0181Hz，低于实测值，但是对无量纲化峰值能量估计较为准确；在高频区，实测风速谱与Davenport谱吻合较好。分析三个经验风速谱与实测风速谱的吻合程度我们可以发现，由于Davenport谱和Kaimal谱只受平均风速的影响，对大气稳定度、湍流形式和地形没有进行考虑，所以估计的只是中性大气层结平稳天气的风谱特征，von Karman谱的影响因素除了平均风速还有积分尺度，但是由于积分尺度对计算采用的方法、时长还有平稳程度的敏感性，很难有一个比较准确的计算，故导致对风速谱峰值频率和高低频区估计略微不准确，但是相对而言还是比较适合描述台风状况下的风速谱特征。

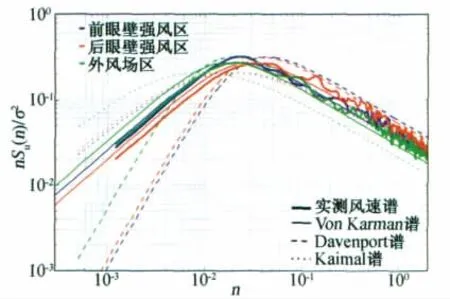
图13 台风不同部位风速谱特征Fig.13 Wind spectra characteristics in different parts of typhoon

比较台风不同部位的三个风速谱特征，可以发现在土木工程所关心的高频区，台风强风区的风谱能量均高于外风场强风区的能量；惯性子区，三个部位风谱均能满足－5／3次律；三个实测风速谱在高频区均介于von Karman谱和Davenport谱估计值之间或与Davenport谱接近；实测台风前眼壁强风区的无量纲化峰值能量最高。

5 结 论

台风荷载已经成为沿海台风影响区高层结构的重要控制荷载。国内外对台风特性的研究基本上是在空旷场地上或结构上安装风速仪进行观测，同时所观测的10分钟平均风速比较小，基本上是台风外风场的常态风，不能较好地反映台风风场特性（强风速、强风切、螺旋结构），很难指导台风影响区结构抗风设计，本文基于近海面观测结果，研究了台风风场特性得出如下结论：

（1）研究了在台风条件下观测到的原始风时程的处理方法，将不合理数据区分为：显著误差、趋势误差和随机误差，并提出了处理方法及台风条件下风速样本选取的原则；

（2）海面上台风条件下，在前眼壁强风区有3°～7°的正风攻角，风眼区和后眼壁强风区，有－1°～2°的风攻角。当在陆地上时，需叠加由于地形影响导致的风攻角；

（3）在台风条件下，下垫面为海面时无论在台风眼壁区还是风眼区，离地100m高度内指数律风剖面指数α均小于规范中A类地貌推荐值0.12。风场前眼壁强风区梯度风高度计算值大于风场后眼壁强风区梯度风高度计算值；

（4）海面实测阵风因子随着平均风速的增大而略微增大。在近海海面3s阵风因子的平均值为1.23；当10分钟平均风速达到17.2m／s以上时，湍流强度基本上不随平均风速变化，在近海海面三个方向湍流强度的平均值分别为0.10、0.07和0.04，Iu∶Iv∶Iw＝1∶0.80∶0.43与规范给出的1∶0.88∶0.52较接近；湍流强度和阵风因子成非线性关系，拟合得湍流强度和阵风因子表达式中两个参数为k1＝0.48，k2＝1.04；

（5）水平向时间尺度基本上小于30s，竖向时间尺度基本上小于10s，与湍流的特征时间尺度一致。积分长度尺度与平均风速具有一定的相关性，极大值比平均风速的极大值略微提前出现。台风前眼壁区积分尺度大于后眼壁区积分尺度；

（6）在双对数坐标系中，前眼壁强风区的峰值频率为0.0232Hz，无量纲化峰值能量为0.3215；后眼壁强风区的峰值频率为0.0427Hz，无量纲化峰值能量为0.2698；外风场区的峰值频率为0.0208Hz，无量纲化峰值能量为0.2706。前眼壁区峰值能量较高，后眼壁区和外风场区峰值能量较接近；在土木工程结构敏感的高频区（＞0.1Hz），实测风速谱均介于von Karman谱和Davenport谱之间。

本文以近海海面台风风场实测数据为基础，研究了台风本身的一些风场特征，为后续的台风风特性研究和结构抗风设计提供一些参考意见，但是由于这方面的观测尚少，结论具有片面性，以后有必要进一步的观测，积累更多的数据，为准确刻画台风风场特性和土木工程结构抗风设计提供更为可靠的依据。

［1］香港天文台.2008年热带气旋：香港天文台［M］.2008.（Hong Kong Observatory.Tropical cyclones in 2008［M］.2008.）

［2］XU Y L，ZHAN S.Field measurements of di wang tower during typhoon york［J］.Journal of Wind Engineering and Industrial Aerodynamics，2001，89（1）：73－93.

［3］CHOI E C C.Wind characteristics of tropical thunderstorms［J］.2000，84（2）：215－226.

［4］黄世成，周嘉陵，王咏青，等.两次台风过程近地层湍流度和阵风因子分析［J］.气象科学，2009，29（04）：454－460.（HUANG S C，ZHOU J L，WANG Y Q，et al.Analysis on turbulence and wind gust factor in surface layer during two typhoon processes［J］.Scientia Meteorologica Sinica，2009，29（04）：454－460（in Chinese））

［5］SARKS P R，HUANG Z.Gust factors and surface－togradient wind－speed ratios in tropical cyclones［J］.Journal of Wind Engineering and Industrial Aerodynamics，2001，89（11－12）：1047－1058.

［6］SPARKS P R.Wind speeds in tropical cyclones and associated insurance losses［J］.Journal of Wind Engineering and Industrial Aerodynamics，2003，91（12－15）：1731－1751.

［7］HARPER B R.Wind speed time averaging conversions for tropical cyclone conditions［A］.AMS 28th Conference on Hurricanes and Tropical Meteorology［C］.Orlando，FL，2008.

［8］LI L X，XIAO Y Q，SONG L L.Study on typhoon wind characteristics based on seashore measurements［A］.Proceedings of the 11th International Symposium on Structural Engineering［C］.Guangzhou，China，2010.

［9］SOLARI G，PICCARDO G.Probabilistic 3－D turbulence modeling for gust buffeting of structures［J］.Probabilitic Engineering Mechanics，2001，16（1）：73－86.

［10］李鹏飞，赵林，葛耀君.上海崇明越江通道工程场地脉动风特性分析［J］.结构工程师，2007（01）：56－61.

［11］孙建超.土木工程相关的近地台风特性观测研究［D］.［硕士学位论文］.哈尔滨工业大学，2006：24－25.

［12］PANOFSKY H A，TOWNSEND A A.Change of terrain roughness and the wind profile［J］.Quart.J.Roy.Meteorol.Soc.，1964，90：147－155.

［13］JTG／TD60－01－2004.《公路桥梁抗风设计规范》［S］.

［14］DEAVES D M，HARRIS R I.A Mathematical model of the structure of strong winds［A］.Construction Industry Research and Information Association［C］.1978.

［15］FRANKLIN J L，BLACK M L，VALDE K.GPS dropwindsonde wind profiles in hurricanes and their operational implications［J］.Weather and Forecasting，2003，18（1）：32－44.

［16］GB50009－2001.《建筑结构荷载规范》［S］.

［17］ISHIZAKI H.Wind profiles，turbulence intensities and gust factors for design in typhoon－prone regions this article is not included in your organization's subscription.［J］.Journal of Wind Engineering and Industrial Aerodynamics，1983，13（3）：55－66.

［18］CHOI E.Wind loading in hong kong－commentary on the code of practice on wind effects hong kong－1983［A］.Council of the Hong Kong Institution of Engineers［C］.1983.

［19］SOLARI G.Wind response spectrum［J］.Journal of Engineering Mechanics，1989，115（9）：2057－2073.

［20］TIELEMAN H W.Universality of velocity spectra［J］.Journal of Wind Engineering and Industrial Aerodynamics，1995，56（1）：55－69.