二维增升装置前缘缝翼的远场噪声分析

刘志仁，王福新，宋文滨，李亚林

（1.上海交通大学航空航天学院，上海200240；2.中国商用飞机有限责任公司上海飞机设计研究院，上海200235）

0 引 言

随着社会的发展和工业技术的进步，国际社会对民用航空业的环保要求越来越苛刻，如何进一步降低飞机的噪声是民用航空业目前面临的一个重要问题。飞机的噪声主要包括两大类：发动机噪声和机体噪声。在航空业发展的初期发动机噪声强度远高于机体噪声，但经过几十年的发展，发动机的喷流噪声已经得到了显著的降低。这使得飞机的机体噪声达到和发动机噪声同等的水平，航空界也越来越重视机体噪声的研究［1］。

已有的研究表明，在飞机的进场和着陆过程中增升装置和起落架是两个主要的噪声源。其中，前缘缝翼是增升装置在飞机起飞和降落过程中最主要的低中频率噪声源。对于一些较新的客机，比如波音777等，前缘缝翼的噪声甚至超过了机翼其它部分产生的噪声［2－4］。因此，研究前缘缝翼的噪声机理以及减噪措施对降低机体噪声具有重要的意义。目前，国外一些学者已经通过风洞实验和数值计算等手段对缝翼噪声的机理、特性进行了研究，研究结果表明前缘缝翼噪声主要来源于缝翼空腔处的紊流及尾缘脱落涡［5－7］。Ma Z和 Smith M 等［8］通过数值计算模拟了安装在缝翼缝道上的声衬的减噪效果，并对声衬的位置和尺寸进行了优化。在国内，对飞机气动噪声的研究还处于起步阶段，研究手段也比较简单，但发展态势良好。游亚飞等［9］采用基于 CFD（Computational Fluid Dynamics，计算流体力学）和FW－H（Ffcows Williams－Hall）理论的方法研究了干净机翼后缘的气动噪声特性，他们认为翼型形状、后缘厚度等对噪声强度存在影响。

另外，增升装置在飞机起飞着陆阶段发挥着重要作用，前缘缝翼的缝道参数是增升装置的主要设计参数，对增升装置的最大升力系数有着很大的影响。因此，本文从工业实际应用出发，通过研究前缘缝翼缝道参数对噪声的影响来分析增升装置的气动噪声和气动性能之间的关系，为工业设计提供参考。Emunds和Fischer［10］采用在平均流场中注入涡的方法分析了带前缘缝翼的二维二段型缝道参数变化对缝翼噪声的辐射方向、频谱的影响，他们认为尽早地在设计过程中将噪声纳入设计参数，能够更好地平衡降噪和气动性能的需求。本文以通用计算流体力学软件FLUENT（v12.1）为平台，先由LES模型计算得到噪声源，然后采用FW－H积分方法获取远场噪声总声压级，分析了缝道参数对远场噪声的影响，并使用响应面对原翼型的缝道参数进行了优化。

1 缝翼噪声计算原理简介

1.1 前缘缝翼噪声源

目前，国外一些研究机构通过风洞试验，测量缝翼产生的流场和噪声频谱等信息，提出了缝翼噪声产生的机理。Takeda和Zhang等［5］通过风洞实验观测了缝翼区域的非定常流场和该区域产生的噪声特性，并成功地捕捉到了缝翼尾缘涡脱落的现象，他们的实验表明，尾缘涡脱落是缝翼尾部噪声的主要来源。这一结论与Khorrami等［7］进行的数值计算结果是一致的。Takeda等［6］人针对缝翼空腔的实验表明空腔表面与剪切层之间的相互作用是低频噪声的来源。一般认为，缝翼噪声源分为低中频和高频两个部分：高频的窄频噪声是由气流经过缝翼与主翼之间的缝道造成的啸叫引起的，而缝翼尾缘涡的脱落是啸叫最主要的原因；低中频率的宽频噪声是由缝翼空腔内各类湍流流动与壁面之间的相互作用造成的。

1.2 气动声学数值计算方法

经过近二十年的发展，计算气动声学已经取得了很大的进步，对航空气动噪声的预测也有了多种方法。计算气动声学方法大致可以分为两类。一类是直接求解法，通过解NS方程直接求取计算域内的声场，这类方法需要的计算成本相当大，以目前的计算机能力来说，还无法进行工程应用。另一类是混合求解法，先用非定常RANS、LES／DES等方法计算声源或者采用RANS加入扰动因子模拟声源，然后再用LEE方法或者FW－H等积分方法计算声波的传播或者辐射［11］。本文采用混合方法，先用RANS求得流场的稳态解，然后以此为初始值用LES方法求解流场的瞬态解，得到噪声声源，最后使用FW－H方程进行积分得到远场观测点的声压随时间的波动。

2 二维增升装置缝翼远场噪声计算

2.1 流场求解器及FW－H声学模型

本文采用的FLUENT商业软件以雷诺平均N－S（Reynolds Averaged Navier Stokes，RANS）方程作为控制方程，使用有限体积法（Finite Volume Method，FVM）进行离散，采用SIMPLEC方法进行速度与压力耦合求解，时间和空间离散精度均为二阶。（1）采用SA（Spalart－Allmaras）湍流模型求解流场稳态解，SA一方程模型其容错功能好，处理复杂流动的能力强，方程中包含对流项，扩散项和源项，以非守恒形式建立。（2）采用LES方法来求解流场中的非定常压力脉动，大涡模拟（LES）采用非稳态的N－S方程直接模拟大尺度涡，但不计算小尺度涡，小涡对大涡的影响通过亚网格雷诺压力模型来近似地模拟。

在FLUENT噪声模块中，用于预测远场观测点噪声预报的方法是基于FW－H方程的声类比积分方法。其基本原理是根据瞬态流场模拟计算结果，获得积分表面脉动压力随时间的变化，然后根据FW－H方程计算得到观测点随时间变化的声压，再通过快速傅利叶变换（FFT）就可以得到观测点的噪声频谱［12］。

2.2 方法验证

由缝翼噪声机理可知，缝翼噪声源主要是偶极子声源，其产生的远场噪声指向性图也明显呈偶极子态。与缝翼噪声类似的是，圆柱绕流的噪声是由涡周期性脱落造成的，是一个典型的偶极子声源［13］。因此，首先计算圆柱绕流的噪声，以验证基于FLUENT平台的远场噪声计算方法是否能有效预测偶极子噪声。

在圆柱绕流噪声计算中，自由来流速度为69.2 m／s，雷诺数为89000，圆柱直径为19.05mm，计算流域为二维矩形区域，坐标原点位于圆柱圆心，计算域的上下和前边界距原点距离为5倍圆柱直径长度，后边界为20倍圆柱直径长度。采用全结构网格，网格结点数为80492，第一层近壁网格高度为0.0005mm，计算的时间步长为5×10－6s。图1显示的是圆柱上方局部的瞬态涡量图，从图可以清晰地观察到涡的脱落过程。

图1 圆柱绕流中涡的脱落Fig.1 Vortex shedding in flow around a circular cylinder

卡门涡周期性的脱落，会引起圆柱表面的压力按涡的脱落频率进行波动。为了验证噪声计算结果是否正确反应了噪声产生的机理，首先对圆柱随时间变化的升力系数进行快速傅利叶变换，得到其频谱如图2所示，图中的峰值频率即为涡的脱落频率。

图2 圆柱绕流升力系数的功率谱密度Fig.2 Power spectral density of lift coefficient in flow around a circular cylinder

卡门涡街脱落的斯德鲁哈尔数一般认为是0.2左右，根据实验的雷诺数不同而有小幅度的不同。表1中列出了计算得到涡脱落频率的斯德鲁哈尔数与物理实验值、经验值的对比。可见本次计算较为准确地预测了亚临界雷诺数情况下的圆柱绕流涡放频率。根据圆柱的噪声机理可知，其噪声频谱峰值频率应该与涡脱落频率一致。在圆柱正上方0.66675m（35倍圆柱直径）的位置设置一个观测点，采用圆柱表面为积分面，使用FW－H噪声模型积分得到该点的声压，通过快速傅利叶转换可得到其频率如图3所示，其峰值频率的斯德鲁哈尔数同样为0.195，与涡脱落频率一致。这一结果说明了，基于FLUENT平台的噪声计算方法是能够正确模拟偶极子声源的噪声产生机理。

表1 圆柱绕流涡脱落频率的斯特鲁哈尔数比较Table 1 Comparison of strouhal number for vortex shedding in flow around a circular cylinder

图3 观测点的噪声功率谱密度Fig.3 Power spectral density of noise at observation point

2.3 几何模型及网格

本文计算中采用UK National High Lift Programme中的L1T2模型［15］。几何外形如图4所示，翼型初始弦长为0.7635m，前缘缝翼的偏角为25°，后缘襟翼的偏角20°，前缘缝道宽度（Gap）为0.0212，缝道重叠量（Overlap）为－0.01，无量纲缝道参数采用的参考长度为翼型弦长0.7635m。该模型的缝翼尾缘尖端与真实缝翼一样，是有一定厚度的。

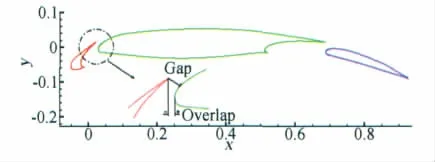
图4 L1T2增升装置模型的几何形状Fig.4 Geometry shape of L1T2high lift device model

本文中计算采用的网格为混合网格，整个计算域中绝大部分网格为结构网格，缝翼附近的网格用四边形的非结构网格代替结构网格，以提高网格对不同前缘缝道参数的适应性，具体网格如图5和图6所示，网格结点数为429，438，计算域为50倍翼型弦长的圆（图中显示的网格进行了稀疏，密度为真实计算网格的1／4）。

图5 增升装置附近的网格划分Fig.5 Grid distribution near high lift device

图6 缝翼附近的网格划分Fig.6 Grid distribution near slat

2.4 远场噪声计算及其结果

对L1T2模型的噪声计算分为以下几步：第一步，采用SA湍流模型求解稳态流场；第二步以流场稳态解为初始值采用LES方法求解瞬态流场；第三步，瞬态流场计算稳定后，加入FW－H声学模型，声源修正长度（Source Correlation Length）设为4m，以缝翼固壁为积分面求解远场噪声。计算的条件为：攻角20.18°，来流速度0.197马赫，计算域半径50倍弦长的圆。

1）图7所示的是SA湍流模型计算得到的L1T2模型表面压力系数与实验值［15］的比较，计算得到的升力系数为3.997（实验值为4.071），计算结果基本与风洞实验值相吻合。

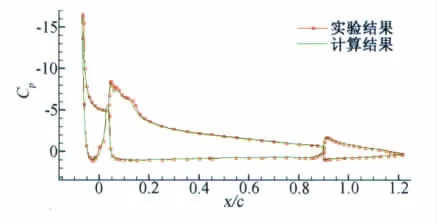
图7 增升装置的表面压力系数分布Fig.7 Distribution of surface pressure coefficient of high lift device

2）非定常计算的时间步长为5×10－6s，迭代步数先为12000步，此时流场结果已经收敛，然后加入FW－H声学模型再迭代9000步，得到观测点的噪声声压。图8和图9是计算得到的瞬态流场中涡量的分布图，从图中可以看出，计算成功捕捉到了缝翼尾缘和空腔内的涡的运动，这些涡的运动是造成缝翼噪声的主要声源。图10显示的是距模型正下方50m远处观测点的噪声频谱。

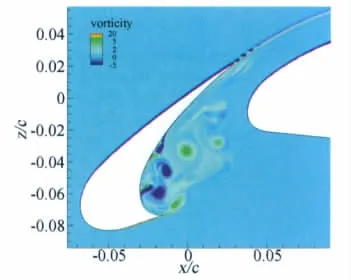
图8 缝翼区域的涡量云图Fig.8 Vorticity contour near slat

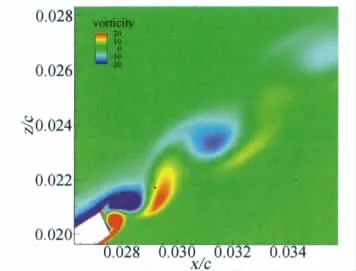
图9 缝翼末端的脱落涡Fig.9 Vortex shedding at slat trailing edge

3）在距模型50m远处，每隔5°取一个观测点，计算观测点的噪声总声压级，得到缝翼噪声辐射的指向性图如图11所示。从图中可以看出缝翼噪声的辐射形态是一个典型的偶极子声源的样式，这个结果与缝翼噪声原理是相吻合的。

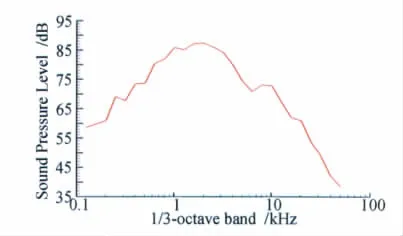
图10 1／3倍频程的声压级频谱Fig.10 Acoustic spectrum in 1／3－octave band

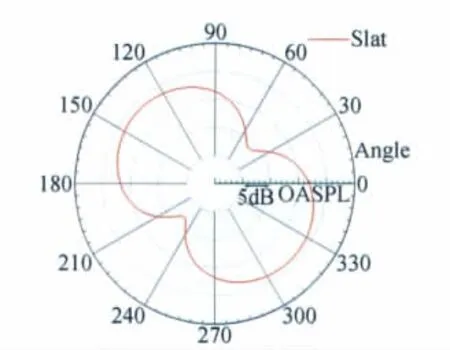
图11 缝翼远场噪声的指向图Fig.11 Far－field directivity pattern of slat

3 二维增升装置的缝翼噪声特性研究

为了研究前缘缝道参数对前缘缝翼远场噪声的影响，首先以L1T2模型为基准模型使用不同的缝道参数构造了24个不同的二维增升装置模型。这些模型的缝道参数分别由5个无量纲缝道宽度值（0.01，0.02，0.03，0.04，0.05）和6个无量纲重叠量（－0.04，－0.03，－0.02，－0.01，0，0.01）组合而成（去除6组不合理的缝道参数）。按照前面计算L1T2模型缝翼噪声的方法，分别计算这24个几何模型的缝翼噪声，噪声的观测点统一设在模型垂直下方的50m处。计算的条件为来流攻角12°，速度0.2马赫。以计算得到的24个总声压级数据为基础，使用优化设计工具OPSYS建立缝翼噪声总声压级关于缝道参数的响应面如图12所示。从图中可以看出，当缝道宽度和缝道重叠量同时增大时，观测点的总声压级先减小再增大，缝道宽度和重叠量都很小或者很大时噪声总声压级显著增大；当缝道宽度减小重叠量增加时，噪声总声压级持续减小。

当然，只分析缝道参数对噪声的影响是不够的，在设计过程中增升装置首先要满足气动性能的要求，因此还应该分析噪声与气动性能之间的关系。为了分析多段翼型气动性能与噪声之间的相关性，同时计算了不同缝道参数对应的最大升力系数，图13中是对应缝道参数组合的最大升力系数云图。将图12和图13比较可知，最大升力系数与总声压级的最优区域并不完全重叠，但是在一定的设计范围内两者还是能够得到较好的平衡。将24个不同增升装置的最大升力系数与噪声总声压级通过缝道参数对应起来，得到图14，从图中也可以看出好的设计是能够很好地满足气动性能和噪声等级两方面要求的。

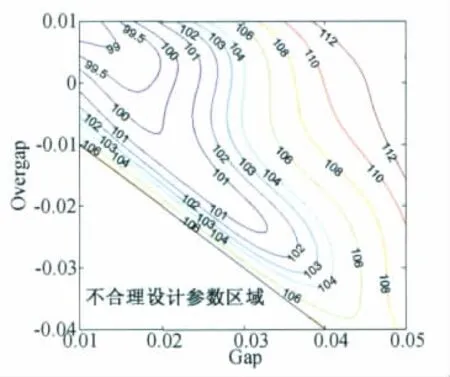
图12 缝翼噪声的OASPL云图Fig.12 OASPL contour of slat noise

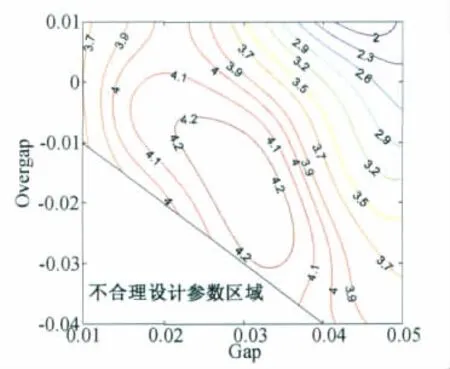
图13 最大升力系数云图Fig.13 Maximum lift coefficient contour

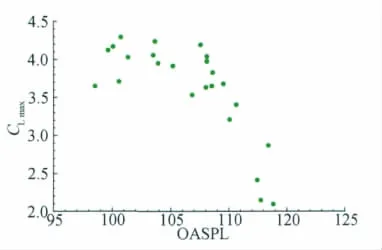
图14 总声压级与最大升力系数的关系Fig.14 Relationships between OASPL and CLmax

4 二维增升装置噪声性能优化

采用两种优化方案，使用OPSYS工具［16］以降低缝翼噪声为目标对L1T2模型的缝道参数进行优化。优化方案一：设定增升装置的最大升力系数必须不小于4.0，才能满足气动性能要求，得到的有效设计参数范围如图15所示。优化方案二：设定增升装置的最大升力系数必须不小于原模型的最大升力系数。优化的结果如表2所示，方案一和方案二得到的噪声总声压级分别较原翼型下降1.07%和0.09%，可以看出原翼型的噪声辐射强度本来就比较低。

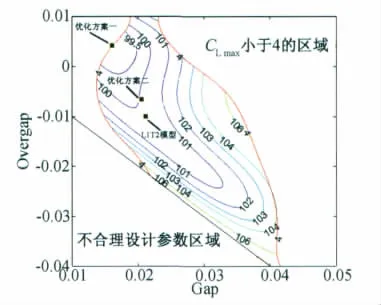
图15 缝翼噪声的优化Fig.15 Optimization of slat noise

表2 优化结果比较Table 2 Comparison of optimized results

5 结 论

本文以计算流体力学软件FLUENT为平台，以L1T2为基准模型，采用LES模型计算了增升装置瞬态流场，并利用FW－H方法计算了远场观测点的噪声辐射。分析了缝翼缝道参数对噪声的影响以及缝翼噪声与气动性能之间的关系，并对L1T2模型的缝道参数进行了优化。得到如下结论：

（1）缝道宽度和重叠量大小适中时，噪声总声压级较小；缝道宽度和重叠量都很小或者很大时噪声总声压级显著增大；当缝道宽度减小重叠量增加时，噪声总声压级持续减小。

（2）最大升力系数和噪声总声压级的最优参数值范围并不完全重合，但好的设计参数是能够使多段翼型同时在气动性能和噪声强度两方面得到优化。

（3）L1T2模型是一个具有较好噪声特性的增升装置模型，但通过优化仍然能够得到少量的改进。

致谢：本研究工作得到中国商用飞机有限责任公司上海飞机设计研究院提供专项资助。

［1］GEOFFREY THOMAS，GUY NORRIS，SMITH C F，et al.Plane simple truth［M］.U.S.：Aerospace Techinical Publications International Oty Ltd，2008：1－208.

［2］DOBRZYNSKI W.Almost 40years of airframe noise research－what did we achieve［J］.Journalofaircraft，2010，47（2）：353－367.

［3］SMITH M，CHOW L.Aerodynamic noise sources on high lift slats and flaps［R］.AIAA Paper，2003－3226.

［4］GUO Y，YAMAMOTO K，STOKER R.Componentbased empirical model for high－lift system noise prediction［J］.JournalofAircraft，2003，40（5）：914－922.

［5］TAKEDA K，ZHANG X，NELSON P.Unsteady aerodynamics and aeroacoustics of a high－lift device configuration［A］.AIAA.40th Aerospace Sciences Meeting ＆Exhibit［C］.Reno，NV，2002：14－17.

［6］TAKEDA K，ASHCROFT G，ZHANG X，et al.Unsteady aerodynamics of flap cove flow in a high－lift device configuration［A］.AIAA 39th Aerospace Sciences Meeting and Exhibit［C］.Reno，NV，2001.

［7］KHORRAMI M R，BERKMAN M E，CHOUDHARI M.Unsteady flow computations of a slat with a blunt trailing edge［J］.AIAAJournal，2000；38（11）：2050－2058.

［8］MA Z，SMITH M，RICHARDS S K，et al.Slat noise attenuation using acoustic liner［A］.AIAA／CEAS 11th Aeroacoustics Conference（26th Aeroacoustics Conference）［C］.2005：1－14.

［9］游亚飞，宋文萍，郝海兵.机翼后缘噪声预测研究［J］.应用声学，2008，27（2）：140－147.（YOU Y F，SONG W P，HAO H Z B.Prediction of trailing edge noise of a clean wing［J］.AppliedAcoustics，2008，27（2）：140－147.）

［10］EMUNDS R，FISCHER M.Effect of slat settings（gap and overlap）on slat noise based on a test vortex injected upstream of the slat hook［A］.AIAA／CEAS.12th Aeroacoustics Conference（27th AIAA Aeroacoustics Conference）［C］.Cambridge，MA：American Institute of Aeronautics and Astronautics，2006.

［11］MA Z.Numerical investigation of slat noise attenuation using acoustic liners［D］.Southampton，UK：University of Southampton；2008.

［12］ANSYS Inc.Ansys fluent 12.1user's guide［EB／OL］.http：／／www.ansys.com／.2009.

［13］ORSELLI R M，MENEGHINI J R，SALTARA F.Two and three－dimensional simulation of sound generated by flow around a circular cylinder［A］.AIAA 30th AIAA Aeroacoustics Conference［C］.2009.

［14］REVELL J D，HAYS A P，PRYDZ A，et al.Experimental study of aerodynamic noise vs drag relationships for circular cylinders［J］.AIAAJournal，1978，16：889－897.

［15］MOIR I.Measurements on a two－dimensional aerofoil with high－lift devices［R］.1994.

［16］SONG W，KEANE A.Surrogate－based aerodynamic shape optimization of a civil aircraft engine nacelle［J］.AIAA Journal，2007，45：2565－2574.