铰接式自卸车前悬架半主动控制及平顺性仿真

郭志军，孟克明，吴静波，李忠利，邢义胜

(河南科技大学车辆与动力工程学院，河南洛阳471003)

0 前言

悬架是现代汽车的重要总成之一，它把车身或车架与车桥弹性地连接起来，其性能的好坏对车辆的乘坐舒适性和行驶平顺性有着重要的影响。因为铰接式自卸车经常行驶在工程现场，所以其路面状况非常恶劣。传统的被动悬架已经不能满足铰接式自卸车的乘坐舒适性和行驶平顺性要求。主动悬架虽然可以满足悬架系统性能的要求，但由于其需要单独的力发生器，所以很难在铰接式自卸车上实现。半主动悬架不需要单独的力发生器且结构简单，能较好地满足悬架系统性能的要求，短时间内其研究和应用的潜力较大［1－4］。

铰接式自卸车因前、后车体之间具有三维铰接式结构，前、后车体所受力与力矩相对独立。所以在平顺性分析过程中，可将前、后两车体分开单独研究［5－7］。前车体主要包括非悬挂质量(前桥、前轮和制动器等)，前悬架和前悬挂质量(前车架、驾驶室、发动机、变速器和液压转向装置等)。后车体主要包括非悬挂质量(中桥、后桥及其相应的制动系统)，中、后平衡悬架和后悬挂质量(后车架、举升系统、车厢及其所装货物)。因为前车体安装有发动机等动力总成，以及对驾驶员疲劳舒适性要求较高，所以，对前车体减振性能要求也较高，故本文重点研究前悬架的动态特性。具体是通过建立前悬架的被动模型、开关型半主动模型和天棚控制半主动模型，分别完成各自的动态特性仿真计算。通过比较悬挂质量垂向加速度、悬挂质量角加速度、悬架动挠度和轮胎相对动载的差异，为该类悬架的半主动减振控制提供了理论依据。

1 前悬架系统动力学模型

1.1 物理模型

铰接式自卸车的前悬架主要由纵向传力元件(“U”型架)、横向传力元件(推力杆)、垂向减振元件(左右共两组螺旋弹簧和左右共4组筒式液压减震器)等组成。建立如图1所示的振动模型，并做以下假设:车辆匀速直线行驶;因驾驶员质量相对于前车体质量很小，所以可忽略驾驶员对于前悬架系统的反向振动影响，即暂不考虑驾驶员——座椅子系统的振动特性;忽略转向、制动和动力系统的振动输入，其质量分别添加到相应位置的车桥和车架上;驾驶室和车架刚性连接在一起，加入其他附件质量形成悬挂质量;车桥、车轮及制动器等组合形成非悬挂质量;车辆对称于它的纵轴线;各弹性元件、阻尼元件均具有线性特性;路面激励仅作用在垂直方向上。

根据标准车辆坐标系规定，图1为背向车辆行驶方向的悬架系统示意图。其中，q1(t)、q2(t)分别是左、右车轮处的路面激励;kt、ct分别是轮胎的刚度和阻尼;k、c分别为悬架的刚度和阻尼;m1、m2分别为非悬挂质量和悬挂质量; J1、J2分别为非悬挂质量和悬挂质量绕纵轴线的转动惯量; l1、l2分别为车辆的前轮距和左右两侧悬架的间距;z1(t)、z2(t)分别为非悬挂质量和悬挂质量质心处的位移;φ1(t)、φ2(t)分别为非悬挂质量和悬挂质量绕纵轴线的侧倾角。

1.2 被动悬架模型

根据图1所建的物理模型，由第二类拉格朗日方程［8］可得到图1四自由度被动悬架的动力学方程

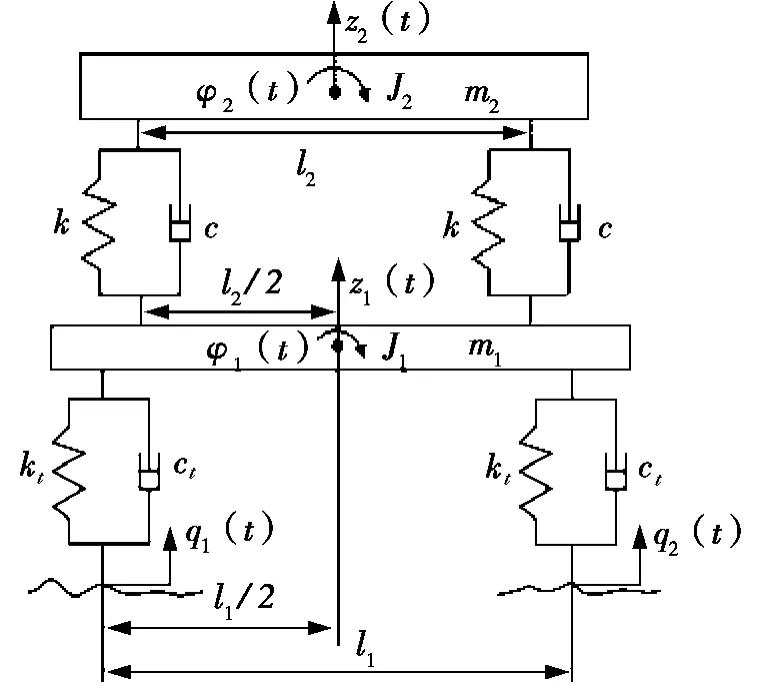
图1 被动悬架

1.3 开关型半主动悬架模型

在式(1)中，由于c为常数，所以不能同时满足各种行驶状态下对悬架减振性能的要求。为此，人为设置惯性墙，在悬挂质量m2和惯性墙之间设置两组虚拟的定常数阻尼器csky，如图2所示。规定所设阻尼器在垂直和侧倾方向上的阻尼力分别为fz和fc。该阻尼力的控制规律如式(2)和式(3)所示。当m1和m2的相对速度与m2绝对速度的符号相同时，阻尼力设置为开状态(具有常数阻尼)，否则为关状态(零阻尼)。把fz和fc分别加到式(1)的第2个和第4个等式的左边，就可以得到开关型半主动悬架的动力学方程。

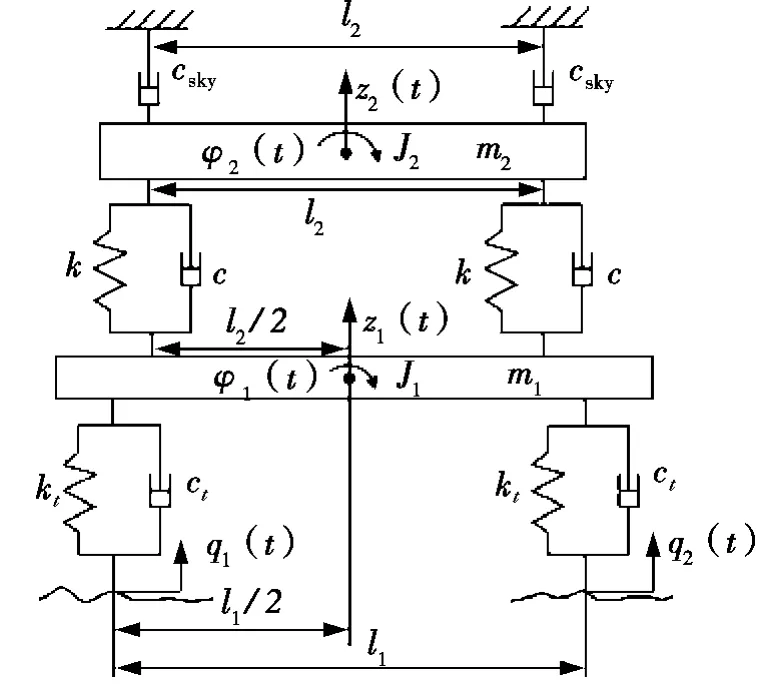
图2 开关型半主动悬架

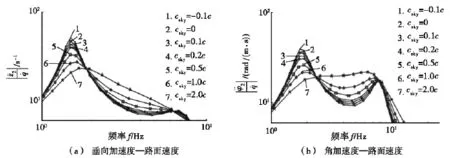
图3 悬挂质量垂向加速度和角加速度对路面速度的幅频特性

从图3中可以看出:随着csky的增大，悬挂质量垂向加速度—路面速度幅频特性在一阶固有频率(1.5 Hz，悬挂质量共振频率)处的共振峰有所下降，在二阶固有频率(6.2 Hz，非悬挂质量共振频率)处的共振峰基本没有变化。随着csky的增大，悬挂质量角加速度—路面速度幅频特性在一阶固有频率(1.8 Hz)处的共振峰有所下降，在二阶固有频率(8.3 Hz)处的共振峰基本没有变化。csky过大时会影响系统的固有特性。综合考虑，本文csky选为0.3c。

1.4 天棚控制半主动悬架模型

上述开关型半主动悬架中，由于fz和fc只有两个值来回切换，且csky为常数，所以仍然不能很好地满足悬架性能的要求。因此，考虑使csky成为阻尼力连续可调的阻尼器—天棚阻尼，来进一步改善系统的减振性能或车辆的平顺性。为了获得天棚阻尼的最优值，利用线性二次型最优控制理论，并考虑控制能量最小的基本条件来求解最优值［9－10］。取目标性能指标为

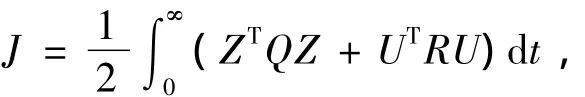
式中，Z为系统状态变量，Z={z2，z2，φ2，φ2}T;U为主动控制力，U={fz，fc}T;Q、R为加权系数矩阵。当某个分量对所研究问题的影响很大，需要特别约束时，就可以加大此分量的权系数;如果此分量对所研究问题的影响很小，就可以设它的权系数为零。根据研究的内容和侧重点，Q、R取值分别为

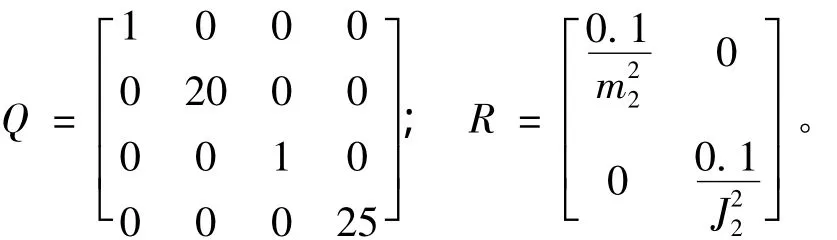
2 仿真分析

2.1 路面激励

选用一个滤波白噪声作为随机路面激励模型，它可覆盖大部分的路面激励频率范围［11］。Simulink仿真模型如图4所示，其数学表达式为

其中，q(t)为路面激励;w(t)为均值为零的白噪声;G0为路面不平度系数;u为车速;f0为下截止频率。因砂石路为铰接式自卸车常用路面，所以路面等级选用C级。因规定选用10 km/h、20 km/h、30 km/h和40 km/h这4种车速［12］，本文所设计铰接式自卸车设计最高车速为48 km/h，常用车速为30 km/h。仿真过程中分别选用上述4种车速作为车速条件，其中，重点分析车速为30 km/h时的动态特性。

图4 随机路面激励模型

2.2 仿真分析

利用Matlab分别做出上述3种悬架的悬挂质量垂向加速度和角加速度对路面速度的幅频特性，如图5所示。从图5中可以看出:开关型半主动悬架的悬挂质量垂向加速度—路面速度幅频特性在一阶固有频率(1.5 Hz)处的共振峰比被动悬架的略低，在二阶固有频率(6.2 Hz)处的共振峰基本和被动悬架的相同。天棚控制半主动悬架的悬挂质量垂向加速度—路面速度幅频特性在一阶固有频率(1.5 Hz)处基本没有共振峰，在二阶固有频率(6.2 Hz)处的共振峰比被动悬架和开关型半主动悬架的都低。开关型半主动悬架的悬挂质量角加速度—路面速度幅频特性在一阶固有频率(1.8 Hz)处的共振峰比被动悬架的略低，在二阶固有频率(8.3 Hz)处的共振峰基本和被动悬架的相同。天棚控制半主动悬架的悬挂质量角加速度—路面速度幅频特性在一阶固有频率(1.8 Hz)处基本没有共振峰，在二阶固有频率(5.4 Hz)处存在共振峰，峰值介于被动悬架和开关型半主动悬架之间。天棚控制半主动悬架虽然可以有效地抑制一阶、二阶固有频率处的共振现象，但是其改变了系统的固有特性，使二阶固有频率减小。

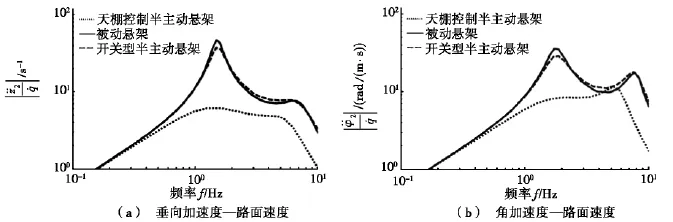
图5 悬挂质量垂向加速度和角加速度对路面速度的幅频特性

当车辆发生侧倾振动时，由于图1和图2中左、右车轮处路面激励不相同，所以仅考虑单边车轮。轮胎动载Fd=kt(z1+l1φ1－q1)+ct(z1+l1φ1－q1)，轮胎相对动载为轮胎动载(Fd)与悬挂质量m2的重力(G)之比，它是一个无量纲物理量。选用悬挂质量垂向加速度(z2)、悬挂质量角加速度(φ2)、悬架动挠度(fd=z2－z1)和轮胎相对动载(Fd/G)这4个参数，对铰接式自卸车前悬架系统进行定量评价。采样时间为0.05 s，仿真时间为20 s。图6是当车速为30 km/h时，上述参数仿真结果的时域曲线。表1为上述参数仿真结果的均方根值。

由图6和表1可得出以下结论:随着车速的增大，悬挂质量垂向加速度、悬挂质量角加速度、悬架动挠度和轮胎相对动载均变大。当车速为30 km/h时，开关型半主动悬架比被动悬架在悬挂质量垂向加速度、悬挂质量角加速度和轮胎相对动载方面分别下降了14.4%、8.7%和2.8%，而在悬架动挠度方面则提高了3.3%。天棚控制半主动悬架比被动悬架在悬挂质量垂向加速度、悬挂质量角加速度、悬架动挠度和轮胎相对动载方面分别下降了48.6%、18.8%、3.2%和9.9%。在其他车速条件下，悬挂质量垂向加速度、悬挂质量角加速度、悬架动挠度和轮胎相对动载的变化规律和30 km/h时的变化规律相同。开关型半主动悬架在悬架动挠度方面变得恶劣，这和csky不能连续平滑可调有关。天棚控制半主动悬架不能使所有参数优化程度相等，这与最优反馈控制矩阵K计算过程中只考虑了悬挂质量垂向加速度和悬挂质量角加速度，没有考虑悬架动挠度和轮胎相对动载有关。

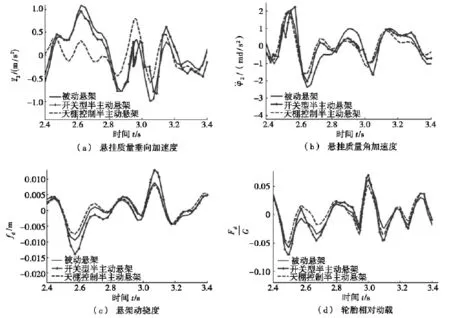
图6 前悬架仿真结果

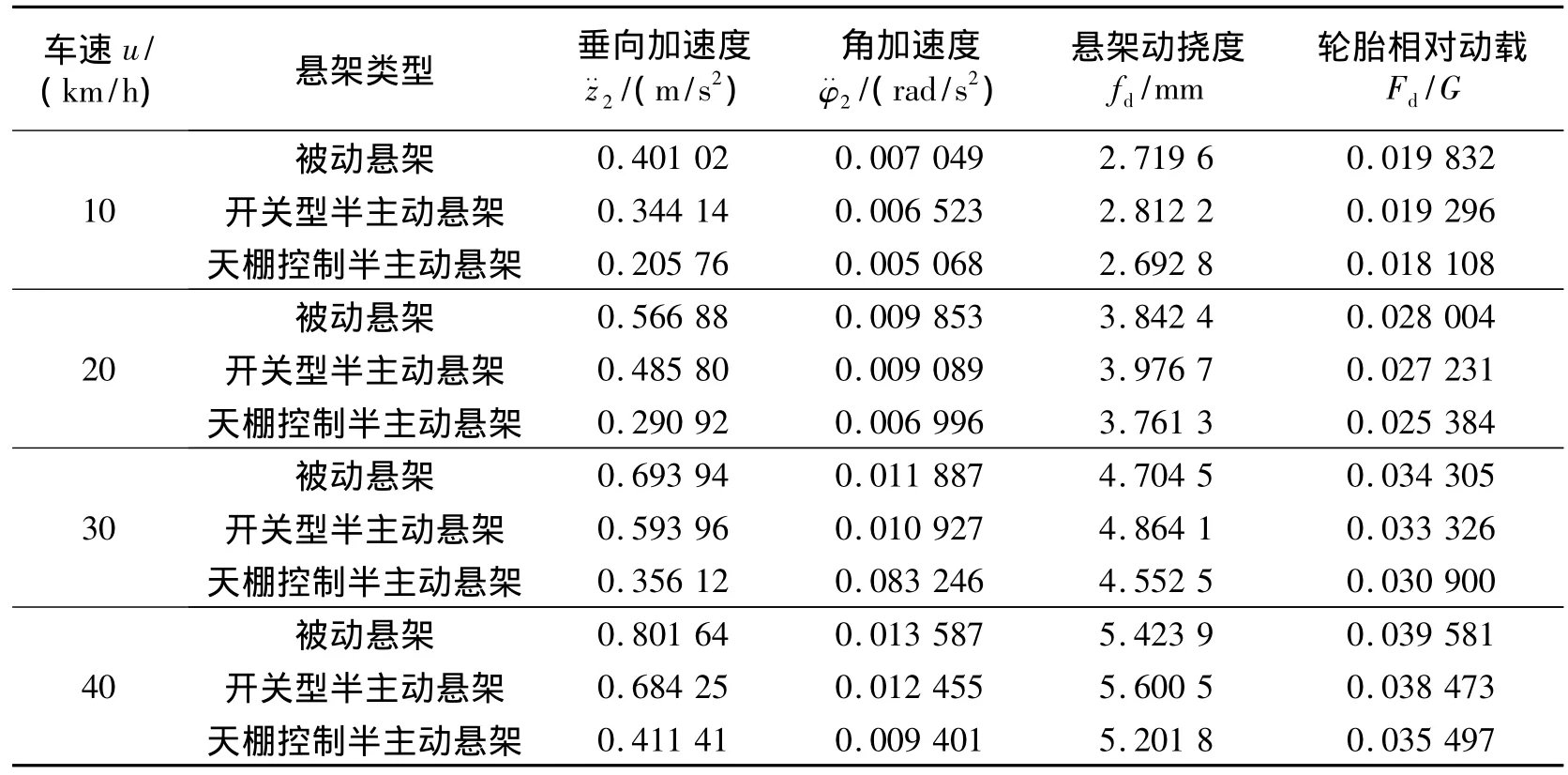
表1 前悬架时域响应仿真结果(均方根值)

3 结论

(1)开关型半主动悬架的开关阻尼值可取为悬架阻尼的0.3倍。

(2)幅频特性分析表明:无论是悬挂质量垂向加速度，还是侧倾角加速度，开关型半主动悬架相对于被动悬架而言，幅值减少有限，共振频率基本没变化。天棚控制半主动悬架则可使悬挂质量的共振峰值约降低一半，振动衰减曲线也变得比较平缓。

(3)随着车速的增大，悬挂质量垂向加速度、悬挂质量角加速度、悬架动挠度和轮胎相对动载均变大。

(4)对于4种车速下，悬挂质量垂向加速度、悬挂质量角加速度和轮胎相对动载等参数的分析计算表明:开关型和天棚控制半主动悬架均比被动悬架减振效果好，而且天棚控制半主动悬架对于振动的衰减能力约为开关型的3倍。另外，开关型半主动悬架有可能使悬架动挠度增加。

［1］ 王国丽，顾亮，孙逢春，等.车辆主动悬架技术的现状和发展趋势［J］.兵工学报，2000，21(z1):80－83.

［2］ 兰波，喻凡.车辆主动悬架LQG控制器的设计与仿真分析［J］.农业机械学报，2004，35(1):13－17.

［3］ Yu F，Crolla D A.An Optimal Self-Tuning Controller for an Active Suspension［J］.Vehicle System Dynamics，1998，29 (1):51－65.

［4］ Dong X M，Yu M，Liao C R，et al.Comparative Research on Semi-active Control Strategies for Magneto-Rheological Suspension［J］.Nonlinear Dynamics，2010，59(3):433－453.

［5］ 张朝杰.铰接式自卸车前悬架系统动力学建模与分析［D］.洛阳:河南科技大学，2009.

［6］ 周长峰，孙蓓蓓，孙庆鸿，等.铰接式自卸车悬架系统动力学建模与仿真［J］.汽车技术，2004(9):15－18.

［7］ 王长新，郭志军，刘美兰，等.铰接式自卸车前车体侧倾振动仿真分析［J］.河南科技大学学报:自然科学版，2011，32 (3):20－24.

［8］ 蒋伟.机械动力学分析［M］.北京:中国传媒大学出版社，2005:81－118.

［9］ 赵研，寇发荣，方宗德，等.汽车天棚控制半主动悬架模型仿真与性能分析［J］.计算机仿真，2006，23(11):233－236.

［10］ 张嗣瀛，高立群.现代控制理论［M］.北京:清华大学出版社，2006:292－307.

［11］ 陈杰平，陈无畏，祝辉，等.基于Matlab/Simulink的随机路面建模与不平度仿真［J］.农业机械学报，2010，41(3): 11－15.

［12］ QC/T76.8—1993 矿用自卸汽车试验方法行驶平顺性试验［S］.北京:中国标准出版社，1993.