凸度偏移的对数母线圆柱滚子接触应力分析
夏新涛,祝世超,贾晨辉,牛荣军
(河南科技大学机电工程学院,河南洛阳471003)
0 前言
为了改善“边缘应力效应”,滚子通常需要修形,使母线带有微量凸度,这样的滚子被称为凸度滚子。在现有的凸度滚子中,对数曲线母线优势明显[1-5],因为它不仅可以极大地改善“边缘应力效应”,而且滚子中部的应力分布也很均匀,有利于提高轴承的承载能力和使用寿命[6-10]。
图1是圆柱滚子母线的对数曲线,其特点是曲线中间部分近似为直线,曲线两端呈变曲率弯曲状分别向滚子左右两个端部的实体收缩。滚子轴线和径向方向分别与坐标轴线x和y的方向平行;对数曲线左右对称,对称线和y轴重合,曲线上的对称点和坐标原点o重合;滚子母线凸度是指曲线在y方向的高度δ。
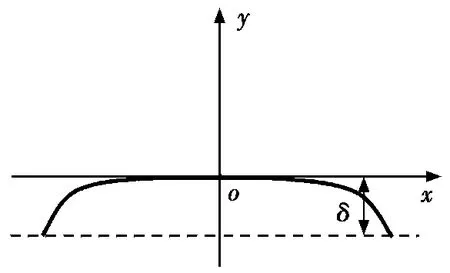
图1 圆柱滚子母线的对数曲线
修形后的滚子母线主要存在3种修形误差:凸度大小误差,凸度偏移误差和凸度形状误差。凸度大小误差是指修形的凸度值和设计值不同;凸度偏移误差是指修形的对数曲线上的对称点与坐标原点o不重合,出现一个偏移量s,如图2所示;凸度形状误差是指修形的滚子母线在法线方向偏离对数曲线的程度。修形误差的存在使滚子与滚道之间的接触状态与理想状态有很大差异,不仅会增大接触应力,而且会使接触应力分布不对称与不均匀,直接影响轴承运动性能和寿命[1-3]。
在现有的文献中,只有关于对数母线滚子凸度大小对轴承接触应力影响的报道[1,3-4],很少有对数滚子母线凸度偏移误差和凸度形状误差对轴承接触应力影响的报道。本文以N1015型圆柱滚子轴承为案例,用ANSYS探讨凸度偏移对滚子与滚道之间接触应力的影响问题,以合理确定对数母线滚子的凸度偏移量。
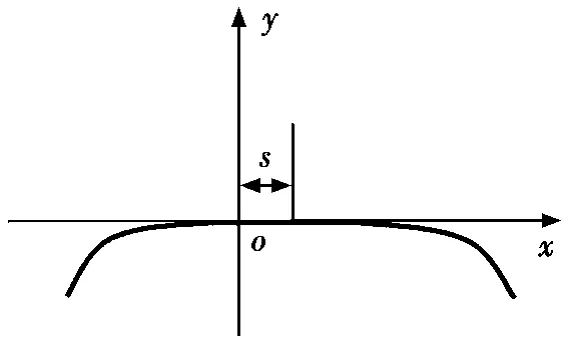
图2 对数曲线的偏移
1 圆柱滚子轴承有限元模型
1.1 轴承主要参数
表1给出N1015型圆柱滚子轴承的主要参数。

表1 主要技术参数
1.2 凸度设计
对数母线滚子的素线方程为
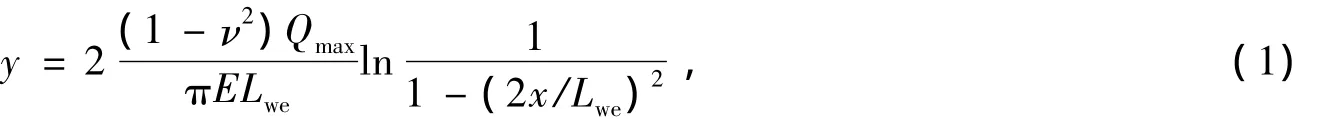
式中,y为对数曲线函数;x为对数曲线函数的自变量,-Lwe/2<x<Lwe/2;ν为滚子材料的泊松比;E为滚子材料的弹性模量;Qmax为滚子承受的最大载荷;Lwe为滚子的有效长度,Lwe=Lw-2r,r为滚子端部的倒角半径,Lw为滚子长度。
实际计算时,取滚子有效长度Lwe=10 mm。
滚子承受的最大载荷为

式中,Fr为轴承内圈所受的径向载荷;Z为滚子个数。
对数母线滚子的建模:考虑到对数曲线在ANSYS中无法直接生成,采用ANSYS的参数化语言APDL建立,其核心内容是宏、参数、循环命令和条件语句,可以通过建立参数化模型来自动完成一些通用性很强的任务,这样可以提高工作效率。
N1015型圆柱滚子轴承部分建模命令流如下:
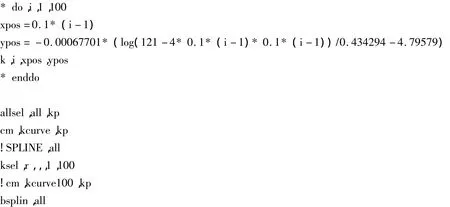
1.3 网格划分
N1015型圆柱滚子轴承二分之一有限元模型如图3所示。采用三维空间连续体8节点线性简化综合单元solid45划分网格。在套圈和滚子的接触部分细化网格,滚子沿轴向方向网格尺寸为0.07 mm,沿径向方向为0.006 mm。远离接触部位的网格,为了减少计算机运算量可以适当稀疏些,对接触应力计算没有影响。当有限元模型的网格边长尺寸小于接触椭圆的短半轴尺寸,特别是小于短半轴尺寸的50%时,计算结果已经足够精确。模型中的滚子与滚道接触区半宽的一半是0.15 mm,所以该有限元模型的网格尺寸是合适的。

图3 N1015型圆柱滚子轴承二分之一有限元模型
1.4 接触对的建立
接触对的建立和接触参数的设定是接触分析中的重要问题[7,10],考虑到内外圈相对滚子的接触情况,把内外圈设为目标面,滚子设为接触面,分别建立接触对。接触刚度和穿透容差是两个重要的接触参数,小的接触刚度有利于收敛性,但大的接触刚度有利于保证精度,因此,需要反复调整才能确定合适的接触参数。经过多次计算,接触刚度因数选为1.5,穿透容差取默认值是比较合适的。
1.5 载荷施加
在施加约束和载荷时,首先,将滚子的一个中间面上所有节点坐标系转为柱坐标系下,剖面加对称约束,约束轴承外圈的外表面节点的所有自由度,约束内外圈和滚子的侧面沿轴向方向的位移,约束滚子中间面上所有节点的周向位移。加载时先将内圈内表面径向自由度耦合,然后在其中一个节点上施加载荷。
2 结果分析
通过上述建模、划分网格、约束、加载和求解,可得到在径向载荷下滚子所受的接触应力、等效应力、径向位移等分析结果。在此通过观察滚子与内圈法向接触应力的变化来分析凸度偏移量对滚子受力的影响。
在给定的0.2倍额定动载荷下,首先分析凸度偏移量为0 mm时的情形,结果如图4所示。由图4可以看出:滚子中部x1=4.9 mm附近(对应于图1中的x=0 mm附近)的接触应力最大,为1 362.846 MPa,但滚子母线表面应力分布左右对称且均匀;沿轴线方向,从滚子中部到滚子端部的接触应力值是逐渐平滑下降的,最小为1 148.2 MPa。研究还表明:滚子与外圈的接触应力小于滚子与内圈的接触应力,但是沿轴线方向的趋势是一样的。
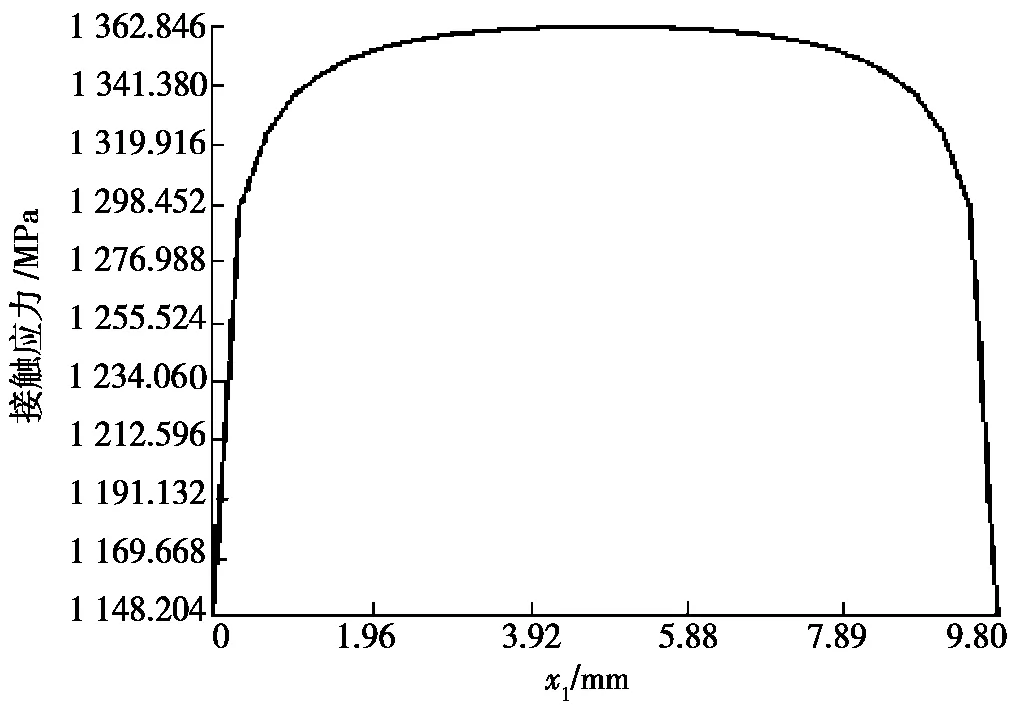
图4 凸度偏移量为0 mm时滚子与内圈的接触应力曲线
图5是对数曲线滚子凸度偏移量为0.7 mm时,滚子与内圈滚道之间的接触应力曲线。由图5可以看出:接触应力的最大值没有出现在滚子母线中部,而是出现在x1=4 mm附近(对应于图1中的x=0.7 mm附近);滚子左端面附近(x1=0 mm附近)与右端面附近(x1=9.4 mm附近)的接触应力分别为1 251.6 MPa和198.1 MPa,两者差值很大。这些表明接触应力的分布呈现出复杂的非对称性与非均匀性,属于对数母线的接触应力分布异常。
图6给出了凸度偏移量从0 mm到0.7 mm范围内的滚子与内圈滚道之间接触应力变化情况。由图6可以看出:在相同的载荷下,凸度偏移量为0 mm时,接触应力分布对称均匀,接触应力大小变化不大。但是,沿滚子轴线方向,随着凸度偏移量的增大,滚子表面最大接触应力和滚子左端表面的接触应力逐渐增大;随着凸度偏移量的增大,滚子右端表面的接触应力下降比较快,尤其当凸度偏移量增至0.4 mm后,滚子右端表面的接触应力下降很快。因此,当凸度偏移量大于0.4 mm以后,滚子左右2个端面的接触应力差值迅速增大,同时滚子表面的最大接触应力逐渐增大,意味着滚子表面应力分布的对称性与均匀性开始变得很差。

图5 凸度偏移量为0.7 mm时滚子与内圈的接触应力曲线
为定量评估表面接触应力的非对称性与非均匀性,图7给出滚子左右端接触应力的相对差。由图7可以看出:随着凸度偏移量的增加,滚子左右端接触应力的相对差非线性增加,在凸度偏移量大于0.4 mm后,滚子左右端接触应力的相对差开始快速增加,表明0.4 mm是一个转折点。在该点,滚子左右端接触应力的相对差约为25%。在工程上,这个百分比是允许的最大相对误差。因此,对N1015轴承滚子的接触应力分布的对称性与均匀性而言,对数曲线滚子的凸度偏移量应控制在0.4 mm以下。这样的制造误差,对于滚子修形质量控制而言,也是比较合适的数值。
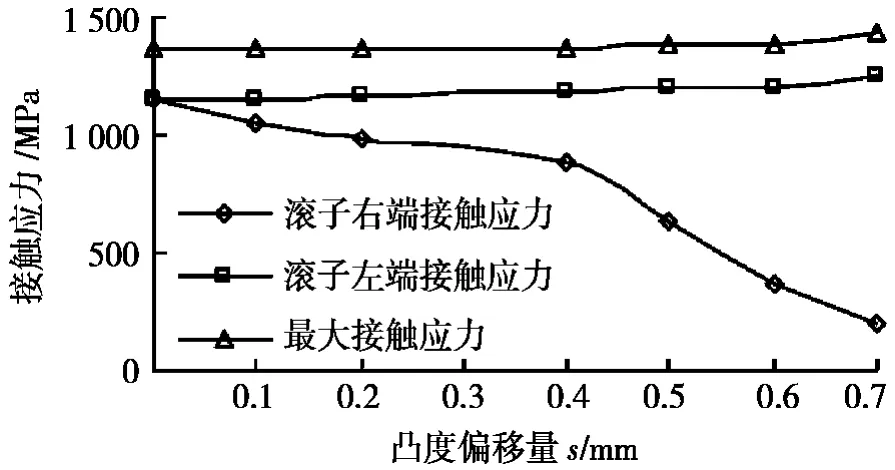
图6 凸度偏移量对接触应力的影响
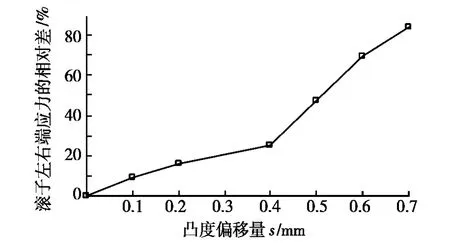
图7 凸度偏移量与滚子左右端接触应力相对差的关系
3 结论
在给定的载荷下,对数曲线滚子凸度偏移量应控制在一定的范围内,否则,滚子与滚道之间的接触应力增大,而且接触应力分布会呈现出复杂的非对称性与非均匀性。在对数滚子曲线修形时,应当严格控制凸度偏移量。对于N1015轴承而言,凸度偏移量应控制在0.4 mm以下。
[1] 陈晓阳,马家驹.对数型滚子凸度量设计中的几个问题[J].轴承,1994(11):2-4.
[2] Harris T A.Rolling Bearing Analysis[M].3 ed.New York:John Wiley&Sons,1991.
[3] Wang L Q,Ye ZH,Gu L.The Effectof Roller Profile Modification on Roller Bearing Performance[J].Advanced Materials Research,2011,230/232:1210-1215.
[4] 孙浩洋,陈晓阳,刘春浩,等.Lundberg对数滚子的热弹流特性及其凸度量的修正[J].摩擦学学报,2008,28:68-72.
[5] 孙浩洋,陈晓阳,张宏信.对数滚子的热弹流凸度量设计研究[J].摩擦学学报,2010,30:567-571.
[6] Demirhan N,Kanber B.Stress and Displacement Distribution on Cylindrical Roller Bearing Rings Using FEM[J].Mechanics Based Design of Structures and Machines,2008,36:86-102.
[7] Slack T,Sadeghi F.Explicit Finite Element Modeling of Subsurface Initiated Spalling in Rolling Contacts[J].Tribology International,2010,43:1693-1702.
[8] Chiu Y P,HartnettM J.A Numerical Solution for the Contact Problem Involving Bodieswith Cylindrical Surface Considering Cylinder Effect[J].Journal of Tribology-Transactions of the ASME,1987,109:479-486.
[9] Hanson M T,Keer L M.Mechanics of Edge Effects on Frictionless Contacts[J].International Journal of Solids and Structures,1995,32:391-405.
[10] Chandrasekara M C S,Ramamohana R A.Mechanics and Behaviour of Hollow Cylindrical Members in Rolling Contact[J].Wear,1983,87:287-296.

