基于引导线的涡轮气冷叶片伸根建模方法

朱 谦 宁 涛 席 平

(北京航空航天大学 机械工程及自动化学院，北京 100191)

1 问题提出

涡轮是航空发动机最重要的结构件之一，是受高温、高压燃气包围以高速旋转并承受高负荷的热端部件［1］.涡轮气冷叶片是空心结构零件，内腔供冷气流通，如图1所示.其结构形状与传热和冷却气流的温度分布关系密切，外形与气动性能、强度等有关，因此结构设计十分复杂，是多专业的技术综合.

从几何建模角度，涡轮叶片分为3个主要部分:叶身、缘板和榫头，如图2所示.叶身和榫头之间的过渡段称为伸根.其外表面是一张光滑曲面，内部有通道连接叶身内腔和榫头内腔，进行结构设计时通道在指定高度上需满足给定的截面面积要求以控制冷气的流速和流量.

伸根段设计是设计人员根据经验多次反复迭代、协调和折衷的过程，设计繁琐工作量大，直接影响整个涡轮叶片设计周期.利用参数化建模方法进行伸根段过渡曲面构造，可以有效的提高设计效率和设计质量.

图1 涡轮叶片内腔结构示意图

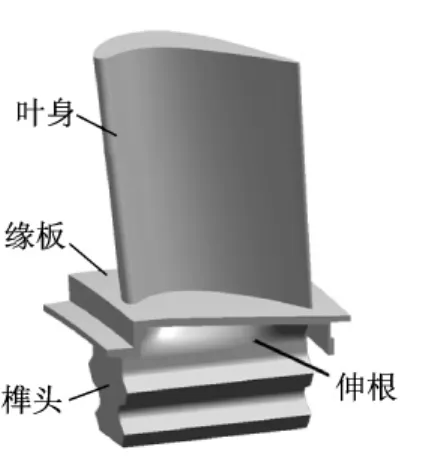
图2 涡轮叶片

文献［2］针对航空发动机气冷叶片进行基于特征的参数化方法研究，提出了叶片内腔由内型反相实体表示，整个叶片由外型实体和内型实体使用布尔差运算得到，实现了叶身特征和部分附属特征的参数化设计，但对伸根的建模方法涉及很少.文献［3］首先通过直纹面放样并与平面相交得到中间截面线，再修改中间截面线，最后用蒙皮法生成伸根内型.这种方法虽然实现了伸根的参数化设计，但仍需一定的人机交互和重复修改工作，并且不容易实现指定高度的截面面积修改.因此本文提出基于引导线的方法完成伸根段的建模:由伸根段的边界条件生成引导线并用最小能量法优化引导线，最终通过引导线放样获得伸根段曲面.这种方法能够进一步减少人机交互，并可以通过修改引导线来实现指定高度的截面面积修改.

2 伸根曲面的特征分析

由于伸根面是叶身和榫头之间的过渡面，首先对叶身和榫头的曲面构造做简要介绍.

叶身外型由多个叶身截面线(又称为叶型)利用蒙皮方法生成，截面线由前缘、后缘、叶盆、叶背4段组成，其中前缘、后缘部分为圆弧，曲率相对较大，叶盆、叶背部分曲率相对较小.叶身内型可由叶身外型截面线串向内等距偏置(等壁厚叶片)或结合壁厚分布要求偏置(变壁厚叶片)所得的截面线串放样生成，其几何特征与叶身外型相似，如图3所示.榫头外型和内型如图4a和图4b所示，在靠近伸根部分的侧面为柱面，上表面都为带圆角的平行四边形.

由于叶片内腔存在多个冷气通道，伸根内型可分为2种类型:完整过渡和局部过渡.完整过渡是由整个叶身内型截面到榫头内型截面的过渡，如图5a所示.局部过渡是叶身内型截面的一部分到榫头内型截面的过渡，见图5c、图5d.伸根外型曲面与伸根内型完整过渡曲面类似，见图5b.

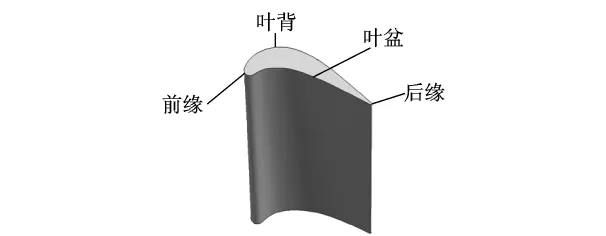
图3 叶片内型/外型示意图

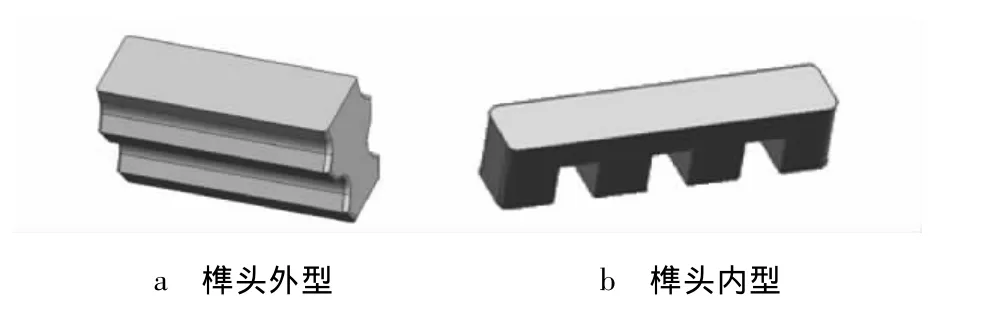
图4 榫头内型与外型

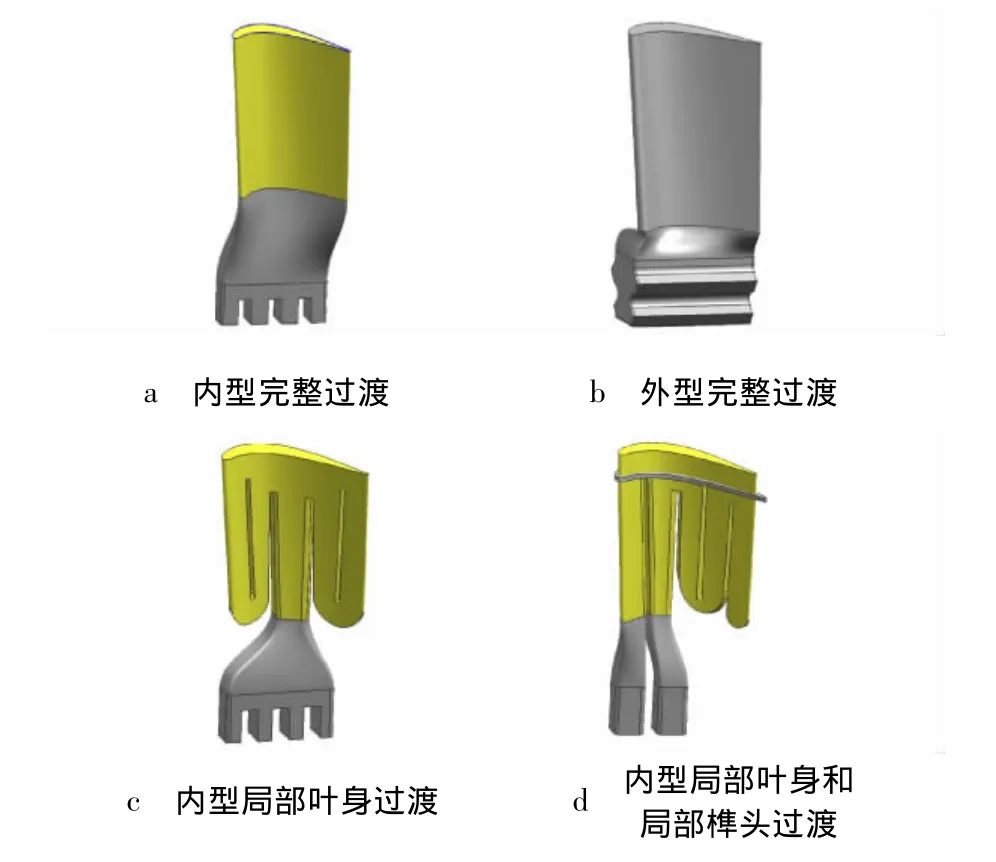
图5 伸根的几种过渡形式

根据叶身和榫头的曲面特点，伸根曲面的特征和建模要求归纳如下:

1)伸根曲面是封闭的自由曲面，连接叶身和榫头，与叶身的连接曲线为叶身截面线，又分为完整截面线或部分截面线，与榫头的连接曲线为带圆角的平行四边形;

2)过渡面与连接面要求达到一阶几何连续;

3)要求在靠近叶身前缘、后缘等曲率变化较大的曲面局部没有扭曲和褶皱，曲面整体光顺，以满足内腔冷气流通的气动要求;

4)实现在指定高度更改内型截面面积以控制冷气流量、流速.

3 基于引导线的伸根建模方法

3.1 基本方法

根据伸根段过渡曲面特征，提出了基于引导线的伸根建模方法:

1)当伸根为完整过渡时，选取叶盆、叶背、前缘、后缘的边界4个点和榫头截面4段倒圆角中心位置的点分别作为关键点相对应，这些点的特征是在截面线上的曲率产生突变，这样可使过渡段实体上截面的前缘、后缘能分别对应下截面的2条短边，叶盆、叶背分别对应下截面的2条长边，如图6a所示;当伸根为局部过渡时，上下截面均选取4段圆弧中心位置的点作为关键点，选取如图6b所示.

2)在上截面的4段曲线上分别按等弧长采样点.对于完整过渡的伸根段，由于前缘、后缘曲率较大，在这2段曲线上的采样点可以取密一些.在下截面对应段分布相同数目的采样点，上下截面的关键点和采样点相互对应，如图7所示.局部过渡伸根类似，不再附图说明.

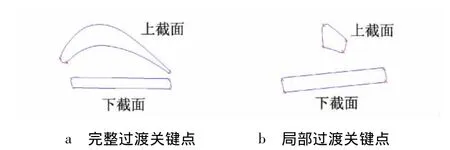
图6 选取关键点

图7 采样对应点

对关键点的选取，可以参考文献［3］采用分离算法自动生成，也可手动选取.手动选取关键点可以根据实际情况调整关键点的位置，具有一定的灵活度.

3)使用样条曲线将上下截面上的对应点连接起来作为引导线，设定引导线两端切矢方向与上下过渡曲面在端点处跨界导矢方向相同.对于由B样条曲面表示的伸根段曲面，可由德布尔算法求取曲面边界给定点处的跨界导矢.图8为引导线切矢等于跨界导矢生成的引导线.

4)根据引导线，对上下两截面线放样，并添加放样曲面两端与叶身内型侧面和榫头内型侧面G1连续的约束条件，从而得到伸根过渡段，如图9所示.引导线是放样曲面的骨架，决定了上下截面线上点的对应方式，防止曲面出现扭曲，从而保证了在截面线方向上的曲面质量，并可通过控制引导线的形状来控制曲面的形状.

使用引导线放样生成曲面可以减少人机交互，避免为提高曲面质量而对曲面直接的手动修改，特别是对曲面上单独点的调整编辑，进而避免了因此产生的曲面局部凹陷或凸起.引导线还使上下截面按照对应点分段对应，减少了曲面整体的扭曲.

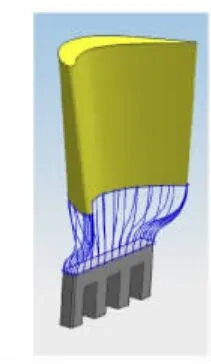
图8 引导线

图9 伸根过渡段

3.2 最小能量法优化引导线

基于引导线所构造的曲面已能满足G1几何连续条件，但引导线两端切矢模长的大小会对引导线以及相应曲面的形状产生影响，如图10所示.因此本文采用最小能量法求解光顺度最高的引导线:当曲线的能量最小时，可以认为其光顺程度最高，进而保证了在引导线方向上的曲面质量.

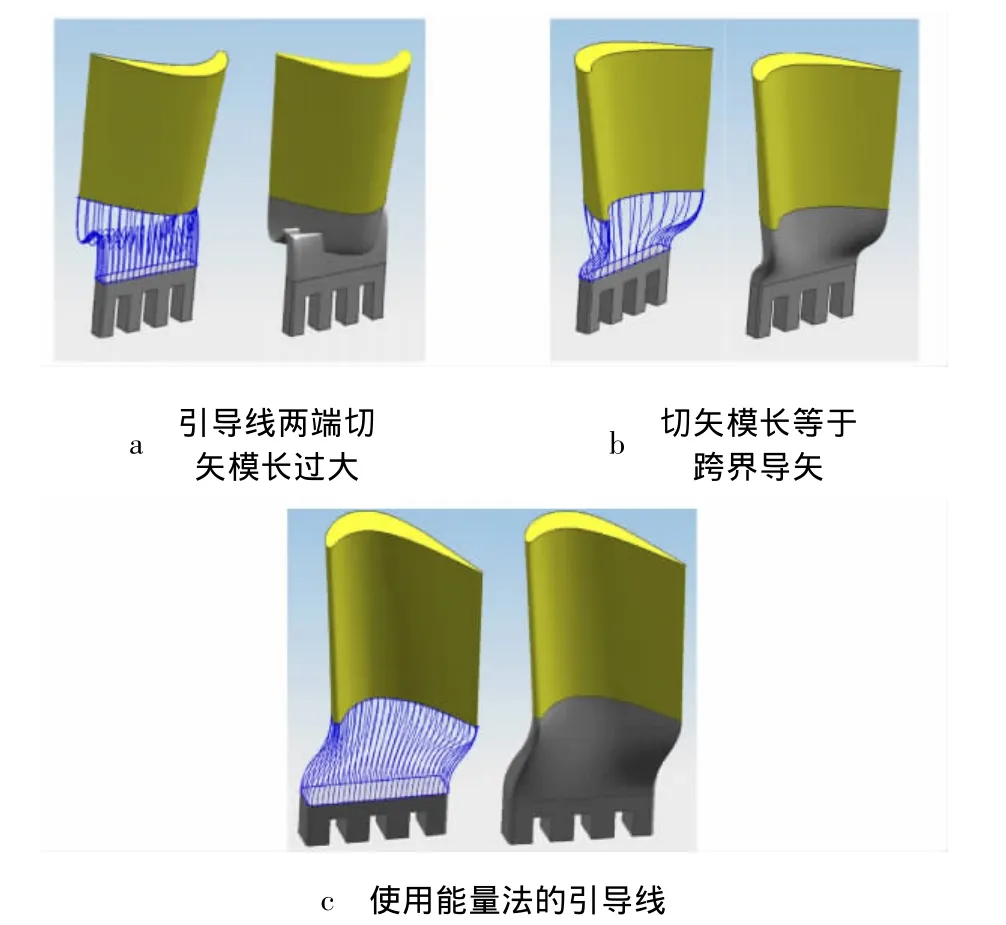
图10 不同切矢模长对引导线和曲面的影响

最小能量法是借鉴弹性力学中薄板的弹性变形方程，以曲线曲面拥有最小物理变形能量为目标，运用各种约束及添加外载荷等方式控制曲线曲面形状的造型方法［4］.根据能量法的概念，每条曲线都能由公式定义出所包含的能量.本文使用曲线的曲率表示曲线的能量模型:对于二阶连续曲线 Q(t)，t∈(t0，t1)，曲线的能量为

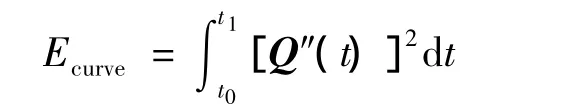
设上下截面对应点的坐标矢量为P0和P1，切矢方向为跨阶导矢V0和V1方向，其中P0=Q(t0)，P1=Q(t1)，V0=Q'(t0)，V1=Q'(t1).则目标函数为

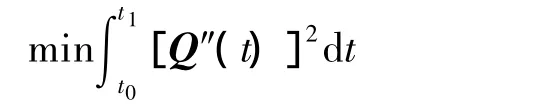
根据参考文献［5］，在以此为边界条件的三次样条曲线族中，能量最小的曲线是以{P0，P1，a V0，b V1}为边界条件的三次样条曲线，其中

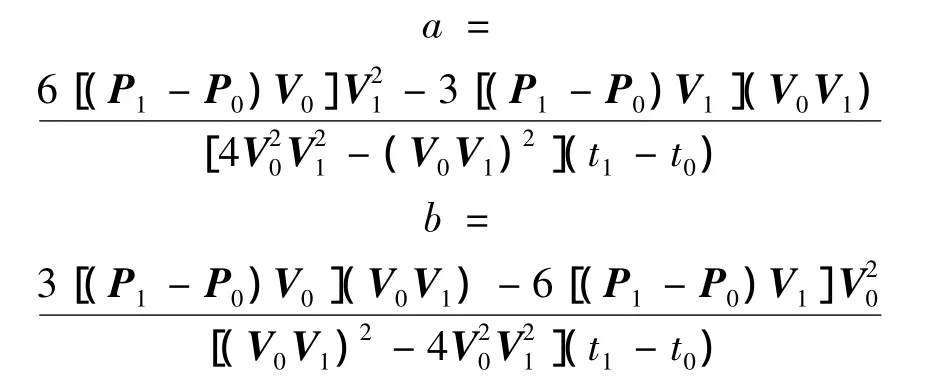
从而求得这2个对应点之间的引导线，同理可得到其余引导线.

效果如图10c所示，可见引导线更光滑，曲面质量更高.

3.3 修改指定高度截面面积的方法

进行伸根结构设计时，伸根内部的冷气通道在指定高度上需满足给定的截面面积要求以控制冷气的流速和流量，这就要求能够修改指定高度的伸根内型截面面积.而借助引导线样条曲线的性质可以达到这个目的，方法如下:

1)将z值设为指定高度，取平行于xOy的平面，与引导线相交于Pi(i=1，2，…，n;n为引导线数).引导线为样条曲线，Pi为引导线上的插值点，如图11所示;

图11 指定高度插值点

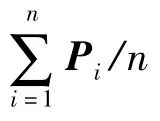
3)更新引导线，进而生成改变截面面积的伸根内型，如图12所示;

4)计算该截面面积，若大于给定的最小截面积，则返回3)，直到该截面面积足够接近给定的最小截面积.

图12 更新伸根内型

3.4 保证伸根最小壁厚方法

为了保证叶片强度，伸根段还要满足最小壁厚要求，保证伸根最小壁厚方法如下:

1)建立伸根内、外型实体模型;

2)求取内型、外型曲面在指定高度之间最小距离;

3)将最小距离与给定的叶片最小壁厚值对比，若大于最小壁厚值，则完成外型建模;若小于最小壁厚值，放大在此高度伸根外型的截面面积，重复2)，直到最小距离大于所给定的叶片最小壁厚值为止.

4 伸根内型/外型参数化建模实现

根据以上方法，本文以VC++6.0为开发工具，在UG NX 3.0平台上利用UG/Open API开发完成涡轮气冷叶片伸根内型/外型参数化设计系统，实现了伸根内型/外型参数化建模.

伸根段设计流程如图13所示，最终效果如图14所示.

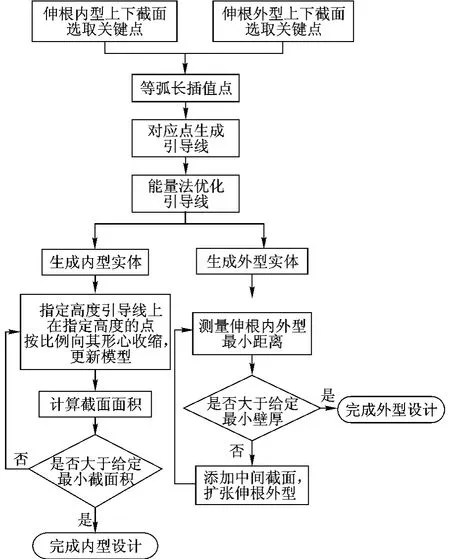
图13 伸根段设计流程

图14 伸根参数化设计实现结果

5 结论

本文针对涡轮气冷叶片伸根段结构特点，提出了基于引导线的伸根段曲面建模方法，实现了伸根内型/外型的参数化建模.此项功能的开发增强了设计过程的连续性和自动化，避免了手动直接修改导致的曲面质量下降和大量的重复工作，提高了设计效率和设计质量.该方法应用于与某发动机设计所的合作项目中，曲面质量得到设计所的认可.此方法也为航空发动机其它复杂过渡段曲面参数化建模提供了参考.

References)

［1］航空发动机设计手册总编委会.航空发动机设计手册第十册［M］.北京:航空工业出版社，2000:5－6 Editorial Board of Aircraft Engine Design Manual.Aircraft engine design manual volume 10［M］.Beijing:Aviation Industry Press，2000:5－6(in Chinese)

［2］宋玉旺，席平.基于特征造型技术的涡轮叶片参数化设计［J］.北京航空航天大学学报，2004，30(4):321 －324 Song Yuwang，Xi Ping.Parametric design of turbine blades based on feature modeling［J］.Journal of Beijing University of Aeronautics and Astronautics，2004，30(4):321 －324(in Chinese)

［3］王睿，莫蓉，印亚群，等.涡轮气冷动叶片伸根段参数化设计方法研究［J］.航空计算技术，2008，38(6):1 －4 Wang Rui，Mo Rong，Yin Yaqun，et al.Parametric design on root extending segment of turbine blade［J］.Aeronautical Computing Technique，2008，38(6):1 －4(in Chinese)

［4］朱心雄.自由曲线曲面造型技术［M］.北京:科学出版社，2000:273－305 Zhu Xinxiong.Design technique of free-form curves and surfaces［M］.Beijing:Science Press，2000:273 －305(in Chinese)

［5］ Yong Junhai，Chen Fuhua.Geometric Hermite curves with minimum strain energy［J］.Computer Aided Geometric Design，2004，21(3):281 －301