可实现定点停泊与轨迹逼近的航天器交会控制
侯云忆
(哈尔滨工业大学航天学院,哈尔滨 150001)
景前峰
(上海宇航系统工程研究所,上海 201108)
马广富
(哈尔滨工业大学航天学院,哈尔滨 150001)
在载人飞船、大型空间站、空间操作、在轨维护等空间任务中,往往需要进行轨道交会,轨道交会过程可能涉及到在某点停泊、逼近等任务.由于进行交会的飞行器其近程导航设备的安装角度与测量范围,以及对接飞行器对接口的位置与对接的特殊要求,往往对停泊点的位置、逼近的轨迹、交会过程的视线角提出特殊的要求.针对这些要求,目前发展出不同的轨道交会方法,如:Vbar逼近、Rbar逼近[1]、视线制导[2]、滑移制导[3]等,但这些方法的使用范围均有一定的局限性,其精度、通用性有其不足之处.如Vbar逼近是沿速度方向逼近,Rbar逼近是沿径向逼近,滑移制导可以实现沿斜线逼近,这3种方法均未实现闭环反馈控制,且逼近轨迹较为单一,容易受到初值误差与干扰的影响,精度难以提高,视线制导虽实现了闭环反馈控制,有较高精度,但其逼近轨迹比较单一,难以实现复杂轨迹的逼近.本文设计了一种可以跟踪目标状态的交会控制方法,对目标状态的运动可以进行随意设定,对状态的跟踪具有精度高、停泊与逼近方式灵活等特点,从而具备在设定点停泊,沿设计轨迹逼近目标的功能,并通过仿真对此算法进行了验证.
1 相对运动动力学建模
1.1 坐标系定义
航天器轨道坐标系原点在飞行器的质心,轴z沿轨道矢径负方向,轴x在轨道平面内与轴z垂直,沿轨道运动的正方向,轴y沿轨道平面的负法线方向.如图1所示.
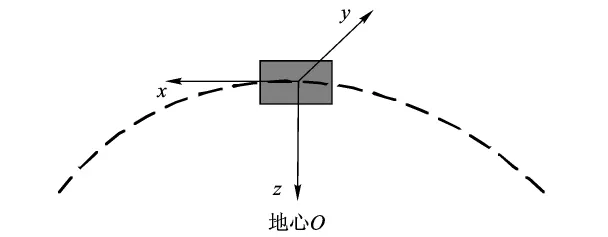
图1 轨道坐标系定义
1.2 相对运动动力学方程
轨道交会任务涉及追踪飞行器和目标飞行器两个航天器.而描述两个近距离航天器的相对运动,最常用的是 hill方程[4-6].记目标航天器为 s,追踪器为c,假设s在近圆轨道上运动,定义交会对接坐标系(即RVD动坐标系)为航天器s的轨道坐标系,即:其原点在飞行器的质心,轴z沿轨道矢径负方向,轴x在轨道平面内与轴z垂直,沿轨道运动的正方向,轴y沿轨道平面的负法线方向.设O为地心,其矢量关系如图2所示.
由矢量关系ρ=rc-rs,及万有引力定律:

图2 两航天器矢量关系
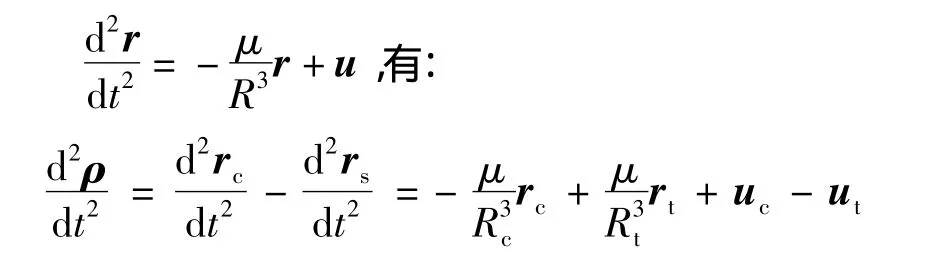
又有其在RVD动坐标系下投影:
考虑到ρ≪R,略去高阶小量,可得相对运动动力学方程:

式中,ns为目标飞行器的轨道角速度;u在轨道坐标系上的投影为 u=[ux,uy,uz].
2 控制算法

其中
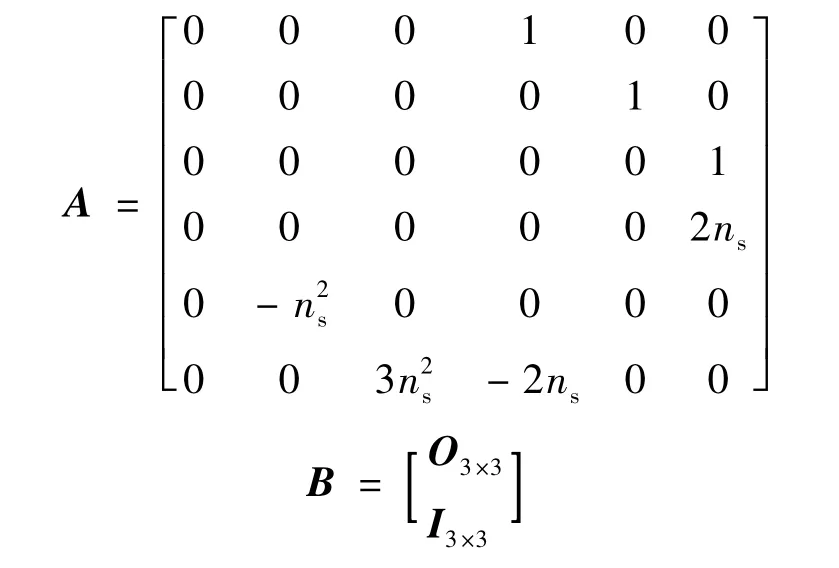
假设一个虚拟目标点D在目标飞行器s后方,与追踪飞行器c的关系如图3所示.
将上述矢量关系代入相对运动动力学方程,可得
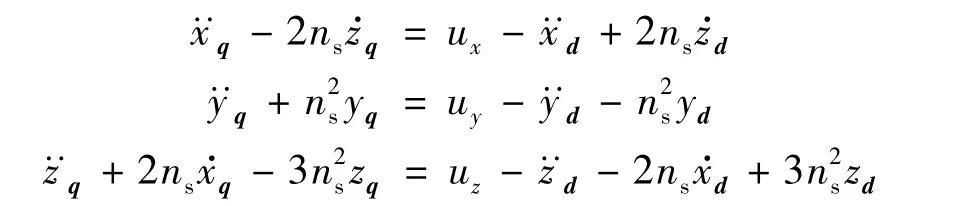
设计以下控制律:
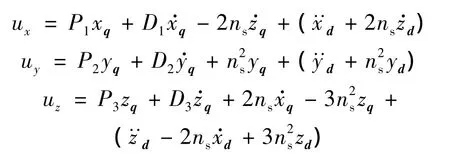
整理可得解耦的3个通道的微分方程:
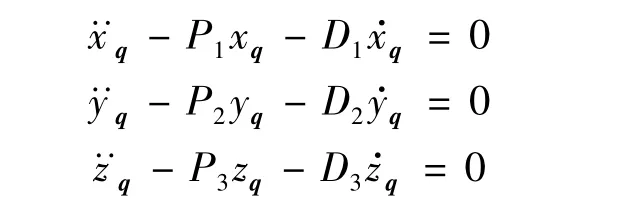
其控制律即
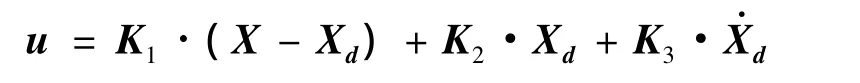
其中

3 定点停泊与轨迹逼近的实现
3.1 在设计点停泊的控制方法

3.2 沿设计轨迹逼近的控制方法
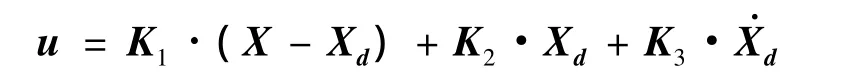
实现沿轨迹逼近的几种典型设计方法有:
1)沿y方向的直线逼近.

2)在轨道平面内沿斜线逼近.
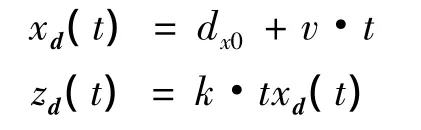
3)沿法向平面螺旋曲线逼近.
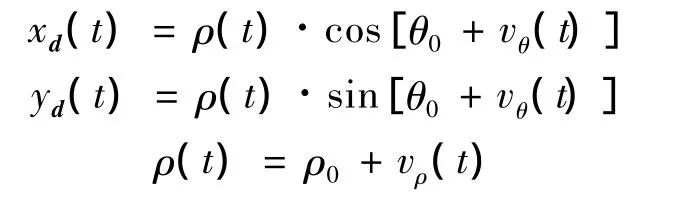
4 仿真分析
进行仿真时,假设轨道高度为400km,初始状态误差为δ.
4.1 在特定点停泊的控制仿真
分别对目标状态为3个轴向1 000m处的定点停泊控制进行了数字仿真,图4~图6给出了3个典型任务在RVD坐标系下的运动轨迹,图7中对比了3次停泊控制的能耗,以便于进行分析.
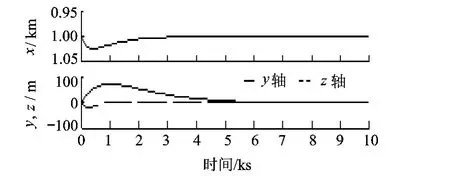
图4 在x轴的停泊

图5 在y轴的停泊
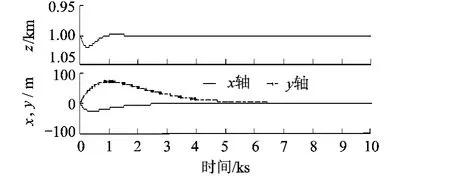
图6 在z轴的停泊
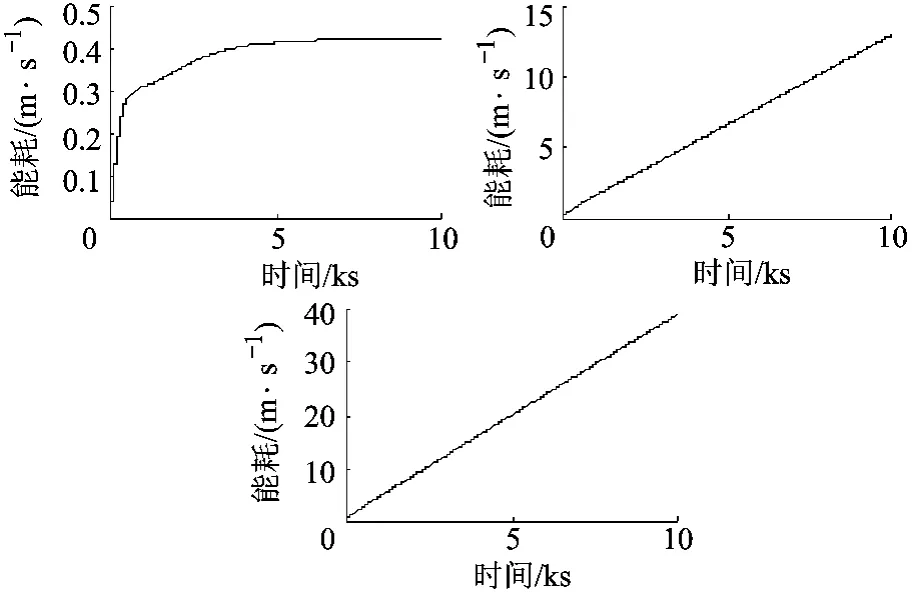
图7 3种停泊的能耗比较(顺序从左至右)
1)在x轴处停泊.
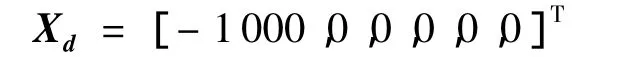
2)在y轴处停泊.

3)在z轴处停泊.

比较在3个轴向停泊控制的结果,包括末端位置精度和能耗,见表1.
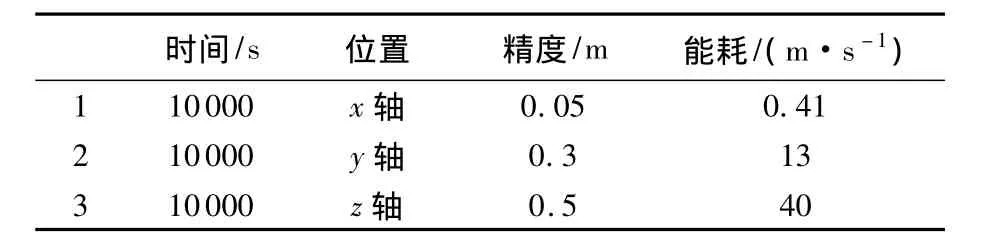
表1 3种典型位置停泊控制性能比较
可进一步分析:在x轴停泊时,只要初始条件符合要求,就可以利用相对动力学自由运动特性停泊于稳定点,因此能耗省、精度高;须控制在y轴、z轴停泊时,由于都不是可以自由停泊的稳定点,需要不断地进行控制,所以有一定的能耗;此外,z轴的停泊控制要更加困难,是因为会有一个漂移速度,需要不断抑制这种漂移,需要的能耗最高.
4.2 沿特定轨迹逼近的控制仿真
设计沿x,y,z3个轴向直线跟踪、在轨道平面内沿z=x斜线逼近、以及沿法向平面Oxy螺旋逼近5种逼近轨迹为目标状态并进行数字仿真.图8~图12依次给出了5次逼近任务在RVD坐标系下的运动轨迹和能耗.
1)沿 x轴逼近(图8):从 -5 km逼近至-1 km处;
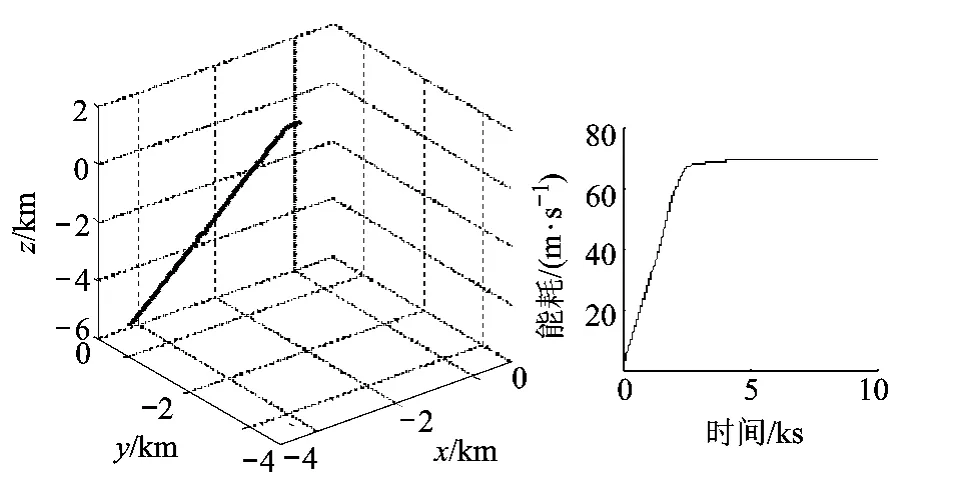
图11 沿z=x轨迹逼近路径与能耗
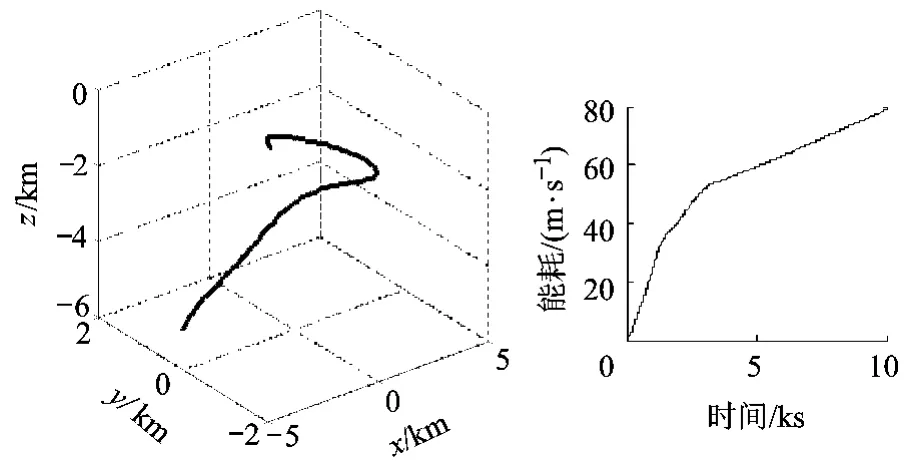
图12 沿Oxy平面螺旋逼近路径与能耗
2)沿 y轴逼近(图9):从 -5 km逼近至-1 km处;
3)沿 z轴逼近(图10):从 -5 km逼近至-1 km处;
4)沿z=x轨迹逼近控制(图11):从-5 km逼近至-1 km处;
5)沿 Oxy平面螺旋曲线逼近(图12):从-5 km逼近至-1 km处.
通过以上5种典型逼近轨迹的仿真与比较,可以分析:当沿x轴逼近时,由于在x轴上有一连串稳定点,可以部分利用相对动力学自由运动特性,所以能耗较省;而在实现沿y轴、z轴、z=x轨迹、Oxy螺旋曲线逼近时,由于影响系统的耦合项较大,能耗较高;同时发现,沿z轴、z=x轨迹的逼近更加困难,同样是因为z不为0时,会有一个漂移相对速度,需要不断抑制这种漂移,所以需要的能耗最高.
针对以上功能实现和控制性能的特点,在逼近轨迹设计的多样性和精度上和其他交会控制方法进行了比较,本文所提出的方法在灵活性和精准性上有较好的表现,见表2.

表2 与其他交会控制方法比较
5 结论
本文针对轨道交会中可能出现的停泊点保持与逼近轨迹的特殊要求,设计了一种可快速跟踪设定目标状态的控制方法,通过数学仿真表明,此种控制方法可以很好地实现在特定点进行停泊保持与沿特定轨迹进行逼近,并且具有精度高、逼近方式灵活等特点.
References)
[1]林来兴.空间交会对接技术[M].北京:国防工业出版社,1995 Lin Laixing.Space rendezvous and docking technology[M].Beijing:National Defence Industry Press,1995(in Chinese)
[2]王颖,吴宏鑫,解永春.基于视线制导的交会停靠控制方法[J].航天控制,2004,22(6):21 -24 Wang Ying,Wu Hongxin,Xie Yongchun.Line of sight guidance based rendezvous and berthing control method[J].Areospace Control,2004,22(6):21 -24(in Chinese)
[3]朱仁璋,尹艳.论空间交会最终平移段制导设计[J].中国空间科学技术,2004,5:1 -8 Zhu Renzhang,Yin Yan.Guidance strategy design for the final translation of space rendezvous[J].Chinese Space Science and Technology,2004,5:1 -8(in Chinese)
[4] Hablani H B.Guidance and relative navigation for autonomous rendezvous in a circular orbit[J].Journal of Guidance,Control and Dynamics,2002,25(3):553 -562
[5]陈统.空间自主交会的轨道动力学与控制方法研究[D].北京:北京航空航天大学,宇航学院,2008 Chen Tong,A study on orbital dynamics and control of space autonomous rendezvous[D].Beijing:School of Austronautics,Beijing University of Aeronautics and Astronautics,2008(in Chinese)
[6] Singla P,Subbarao K,Junkins J L.Adaptive output feedback control for spacecraft rendezvous and docking under measurement uncertainty[J].Journal of Guidance,Control,and Dynamic,2006,29(4):892-902

