抽样调查中基于模型的稳健预测方法

巩红禹，贺本岚，王丽艳

(1.内蒙古财经学院，呼和浩特010051；2.中国人民大学 统计学院，北京100872；3.内蒙古岱海发电有限责任公司,内蒙古 乌兰察布 013700)

0 引言

在实际的抽样调查中，通常关注总体的某些特征，如总量、均值、比例等。基于设计推断和基于模型的推断（Fuller,2009;Bolfarine,Zacks,1992;Cassel,Sarndal,Wretman, 1977）是推断有限总体特征的两种不同途径。基于设计推断通常假定总体固定和有限的，根据样本观测结果推断总体的参数。调查者根据某种抽样设计从总体中随机获取样本，样本中每个样本单元的权数是它包含概率的倒数。基于模型推断方法思想是假设有限总体是某个超总体或者某个概率分布的一次随机实现，估计量是基于这个超总体模型作出的。在特定的超总体模型下寻找最优估计是理想的情形，实践中很难找到严格服从某一特定分布的观测数据，于是在假定模型下寻找稳健估计。估计量的稳健性是指，当模型发生微小变化时，对估计量的影响也相对较小。

一直以来，抽样技术领域中估计量的稳健性问题始终受到关注，统计学家从两种途径研究这类问题，一类是讨论样本中有代表性异常点情形，比如和Chambers（1986）和Gwet、Rivest（1992）讨论了样本中有异常点时总量稳健的比率估计,Kuk(2001)给出异常点情形下均值的稳健估计；一类是讨论当模型识别错误时，选择模型下估计量的稳健性问题（Royall,Herson,1973；Scott,Brewer,1978；Royall, Pfeffermann 1982;Rodrigues 1985;Bolfarine,Pereira 1987；tam,1995）。本文拟从后一角度讨论。总体总量的比率估计和扩张估计在简单平衡样本下是稳健的，也就是说，比率估计和扩张估计的无偏性不受模型识别错误的影响。

1 最优无偏估计BLU

设U={1,2,…,N}表示容量为N的有限总体，yk为U中第k个单元的未知观测值；xk1,xk2,…,xkp为第k个单元已知的p个辅助观测值；k=1,2,…,N。假定超总体回归模型M

其中，X=(x1,…,xN)T，xTk=(1,xk1,…,xkp)是已知矩阵，β=(β0,β1,…,βp)T是未知的常量向量，var(e)=V =diag(v1,…,vN)是对角矩阵，第k个对角元素是已知的非负常量。辅助向量值xk是已知的。

超总体回归模型引入了一种新的随机性——总体的随机性，有限总体y=(y1,y2,…,yN)T视为独立随机向量Y=(Y1,Y2,…,YN)T的一个随机样本。

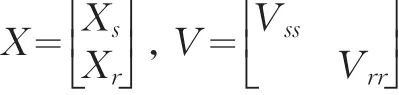
其中：

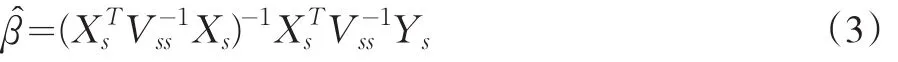
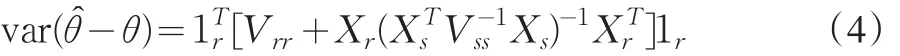
当仅有一个辅助变量与目标变量相关时，通常考虑多项式模型

2 基于简单平衡的稳健估计

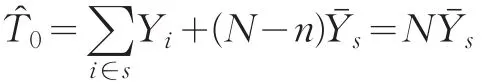
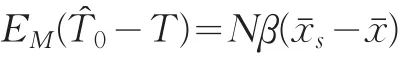
为说明问题的方便，这里正式引入简单平衡样本的概念。记s(J)为满足下面条件的样本，对于j=1,…,J，有

当β0＞0时，若前n最大的x值入样，估计量将会产生最大的负偏倚。如果xˉs=xˉ，比率估计在这个模型下是无偏的。从这里看出，如果总体的ξ*是比率估计模型，抽取前n个最大的x值会使模型方差达到最小，但如果总体的ξ*是含常数项的一次回归模型，这种抽样策略却使估计产生最大的负偏倚。

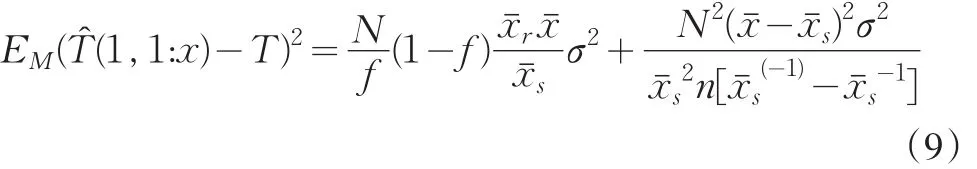
比较（8）与（9）式，若

即使在模型发生微小变化的情形下，采用比率估计不会造成均方误差大的波动。如果样本是平衡的，二者的模型均方误差相同，这时比率估计不失为好的估计方法。

进一步思考，若总体的ξ*是多项式模型，平衡样本能否使得比率估计与扩张估计稳健呢？采用扩张估计的偏倚是

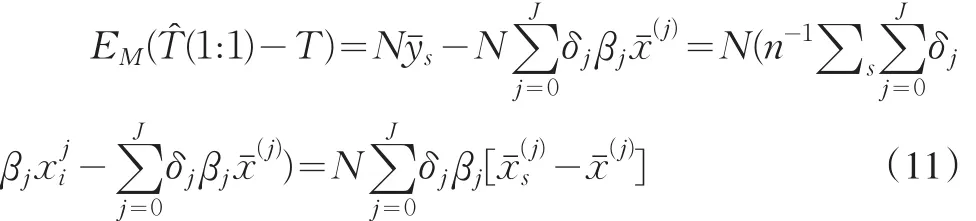
采用比率估计的偏倚是

其中，j≠1（j=1时，（12）式为0）。

如果s=s(J)，那么扩张估计偏倚和比率估计偏倚都是0。满足多项式模型，采用简单平衡抽样设计，比率估计和扩张估计都是无偏估计。这意味着，对于满足多项式模型的总体，采用简单平衡抽样设计，总量比率估计和简单估计是能够消除偏倚的稳健估计。

在简单平衡抽样设计下，总量估计和比率估计既然都是无偏的，我们应该选择哪个估计呢？有两点理由选择比率估计。（1）比率估计充分利用了总体的辅助信息，特别在样本量很小时，扩张估计的结果容易受人质疑，比率估计要明显优于扩张估计；（2）实践当中，样本是很难实现精确平衡的，只能获得近似简单平衡的样本。很多数值分析表明，对不同偏离平衡程度的样本，扩张估计同比率估计相比要更加敏感。

3 平衡样本下比率估计的有效性

如果超总体模型是M(0,1:x)，比率估计的均方误差是（9）式。最优样本满足条件

这时均方误差是最小的，比率估计是最有效的。但如果超总体模型是M(1,1:x)，采用平衡抽样设计消除比率估计的偏倚，这时误差均方误差是

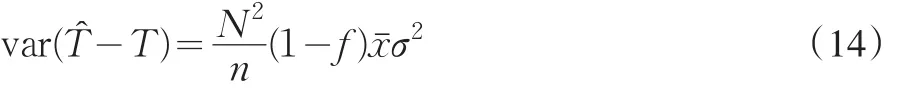
4 约束的简单随机抽样

那么，就认为这个样本是近似平衡的。这个过程可按如下操作：

(1)指定常量E。

(2)采用无放回简单随机抽样。

(3)如果满足条件（16），保留样本；否则将样本放回总体，重复步骤（2）。

E的选择是任意的，当E=∞,是无约束的简单随机抽样。大样本时e(s)是近似服从标准正态分布的。当e(s)＞1.96或者e(s)＜-1.96时，将以0.05的显著性水平拒绝xˉs=xˉ，即认为样本是不平衡的。

这里采用S_PLUS软件模拟平衡抽样设计样本的结果（图1）。

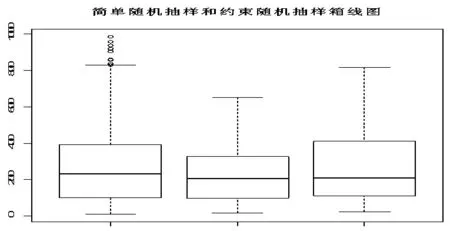
图1

这个总体中，总体单元数是N=393，xˉ=274.6972，我们分别采用简单随机抽样和约束随机抽样（e(s)=0.01）从中抽取样本量为50的样本。图1中，从左至右依次为总体x值、简单随机样本x、约束简单随机样本x的箱线图，简单随意样本均值为 xˉ1=236，约束随机样本均值为xˉ2=274.6972。从图中看出，由约束简单随机抽样获取的样本与总体的分布是很相似的。

5 样本量的确定

如果样本是简单平衡的，样本量可以通过变异系数确定。

基于模型总量的变异系数定义为：

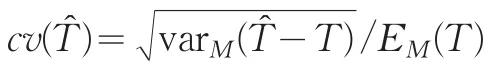
cv是无单位测度，通常认为相对合理的变异系数cv≤10%。cv的平方称为相对方差。为确定样本规模，需要事先设定cv的值。

若总体的真实模型是多项式模型M(δ0,δ1,…,δj:v)，选择模型是M(1:1)，简单平衡样本使得T＾(1:1)是无偏的，其对应的方差为：

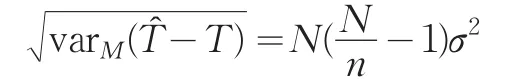
相对方差：

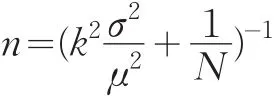
确定样本规模需要事先知道合适的变异系数k、总体均值μ和方差σ2。

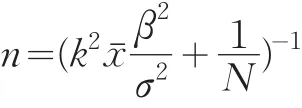
确定样本规模需要事先知道合适的变异系数k、总体均值xˉ和方差σ2。

6 结论

有限总体认为是超总体的一次随机实现，并假定样本分布与超总体的分布是一致的，如果违背模型假定，基于模型作出有限总体参数的推断受人质疑，因此需要考虑基于模型估计量的稳健性问题。本文考虑为了消除估计量的偏倚，假定多项式模型成立条件下，可以对样本进行平衡抽样设计，这时比率估计和扩张估计是无偏估计。

简单平衡样本视为样本单元的权重是相同的，即每个样本单元都代表相同数目的总体单元。事实上，每个单元目标变量的变异并不相同，可能与辅助信息有关，比如医院接纳病人能力的不确定性与病床数相关，消费能力的不确定性与收入有关等。不同变异程度样本单元的权重应该是不同的，即每个样本单元代表总体单元的数目不同。因此，基于模型的抽样设计一种合理的假设是样本单元的权数与方差的平方根成正比，它涉及到权平衡的概念。这是笔者今后面将要研究的问题。

[1]Anthony Y.C.Kuk,A.H.Welsh.Robust Estimation for Finite Populations Based on a Working Model[J].Journal of the Royal Statistical Society,Series B(Statistical Methodology),2001,2(63).

[2]A.J.Scott,K.R.W.Brewer,E.W.H.Ho.Finite Population Sampling and Robust Estimation[J].Journal of the American Statistical Association,1978,6(73).

[3]Claes-Magnus Cassel,Carl-erik Sarndal,Jan Hakan Wretman.Foundatations ofInference in Survey Sampling[M].New York:John Wiley&Sons,1977.

[4]Carlos Alberto de Bragança Pereira,Josemar Rodrigues.Robust Linear Prediction in Finite Populations[J].International Statistical Review/Revue Internationale de Statistique,1983,3(51).

[5]Heleno Bolfarine,Shelemyahu Zacks.Prediction Theory for Finite Populations[M].New York:Springer-verg,1992.

[6]Josemar Rodrigues,Heleno Bolfarine,André Rogatko.A General Theory of Prediction in Finite Populations[J].International Statistical Review/Revue Internationale de Statistique,1985,3(53).

[7]Jean-Philippe Gwet,Louis-Paul Rivest.Outlier Resistant Alternatives to the Ratio Estimator[J].Journal of the American Statistical Association,1992,12(87).

[8]Raymond L.Chambers.Outlier Roubust Finite Population Estimation [J].Journal of the American Statistical Association,1986,12(81).

[9]Richard M.Royall,Dany Pfeffermann.Balanced Samples and Robust Bayesian Inference in Finite Population Sampling[J].Biometrika, 1982,2(69).

[10]WayneA.Fuller.SamplingStatistics[M].NewYork:JohnWiley&Sons, 2009.