基于数据挖掘的股票指数涨跌概率推断

彭益

（湖南大学 金融与统计学院，长沙 410079）

0 引言

股票的价格由股票的价值所决定，价格围绕价值上下进行波动。通过对股票内在价值以及其价格的表现形态进行分析，可以了解股票价格的波动性。对股票的内在价值进行分析，即基本面的分析，主要是结合公司的经营业绩与行业的发展前景，对公司的未来现金流进行预测，从而确定公司未来的价值。当价格高于价值时卖出，当价格低于价值时买入。对价格的表现形态进行分析，即技术分析，主要是对公司股票的历史价格、成交量等交易数据进行挖掘，找出其规律。在此基础上，对股票价格走势进行预测，进而确定当前价位对应的交易策略。基本面分析是一种长期的投资工具，本文欲对短期股指涨跌概率进行推断，故未考虑基本面分析。

从股票产生之日开始，对股票价格以及股指涨跌的预测是学术界与股票投资者感兴趣的问题。对投资者而言，对股价的预测准确度越高，有利于其获得利润与回避风险。对国家的经济金融发展而言，股票市场是国民经济的晴雨表，股票预测也具有重要的作用。针对这样的情况，本文提出推断股指涨跌概率的新方法，通过数据挖掘，用泊松分布拟合股指收益率的动态过程，从而构造股指涨跌概率推断模型来对股指涨跌概率进行预测。

1 基于数据挖掘的股指涨跌概率推断模型

股票指数涨跌变化可以看成离散的时间序列，日收盘价是时间的函数。若进行技术分析，实际上是在知道股票指数第t天以前信息基础上，对第t+1天股票指数 pt+1进行预测。 pt+1是一个非线性的函数，近期的技术分析集中分析收益率动态过程，主要是利用神经网络以及生存模型对股票价格及股指涨跌进行预测。本文也从收益率动态过程的角度出发，对历史数据进行挖掘，采取泊松分布对股指涨跌的动态过程进行拟合，并且以该泊松分布为基础，构建股指涨跌概率推断模型，从而判断第t+1天的股指相对第t天是涨还是跌。

1.1 基于历史数据的泊松分布拟合

对第t+1天股指涨跌进行预测前，可以计算出股指历史日收益率。第t天股指收益率为rt，收益率计算采用rt=(pt-pt-1)/pt-1，其中 pt表示第t天收盘价，pt-1表示第t-1天收盘价。

我国股票市场存在10%的涨跌停限制，每天股票收益率在-10%与10%之间波动。股票指数采取的是派许加权综合价格指数方法进行计算，故其日涨跌幅也在-10%与10%之间。将收益率总区间[-10,10]划分为n等份，则每个区间段的长度为20 n。用i表示区间序号，i取值从1到n，第i区间段表示为Sector(i)，则：

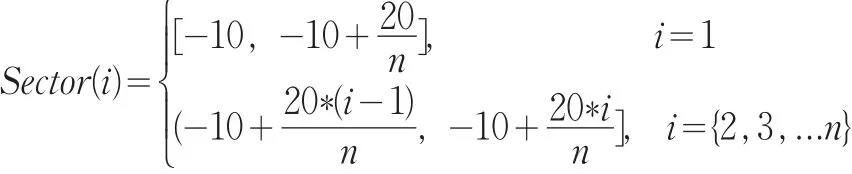
在收益率区间划分为n等份后，可以判断第t天股指收益率rt所处的区间，若rt在区间a(a∈Sector(i))内，将历史数据中出现股指收益率处于区间a后第二天数据组成一个集合S，用该集合来进行泊松分布的拟合。用Count(i)表示集合S中股指收益率在区间段Sector(i)元素个数，P(i)表示集合S中股指收益率在区间段Sector(i)中概率，则：

假设第t+1天收益率rt+1服从参数为λ的泊松分布，且

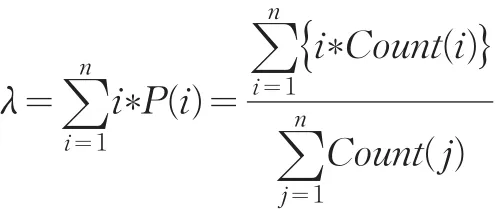
1.2 分布参数的估计

泊松分布的拟合是在收益率区间划分为n等份基础上进行的，需要获得n的最佳值，使得集合S中股票指数收益率尽量服从泊松分布。令n的拟合评估函数为F(n)，现在考虑影响F(n)的元素。

最后，我们希望集合S中股指收益率的实际概率分布是尽量光滑的曲线，考虑股指收益率分为n个区间后，集合S股指收益率实际概率出现异常点的情况。如图1所示，异常点是指在处于某区间的实际概率比其左右临近区间的概率都要低的情况。图1中，收益率区间划分为15个区间段，纵坐标为对应的概率值，则点4为异常点。异常点的个数g(n)越多，表示实际概率分布越不平滑。异常点的个数与 f(n)呈负相关关系。

图1 异常点示例图

对异常点g(n)进行定义如下

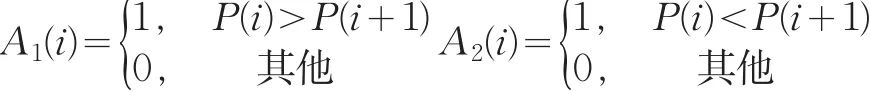
其中 P(i)表示集合 S中股指收益率在区间段Sector(i)中的实际概率，h表示收益率区间进行等分后，集合S中包含元素最多的区间段，即P(h)=max{P(i)}，i∈{1,2...n}。

根据以上三个主要的影响因素，建立了最佳泊松分布的拟合评估函数：

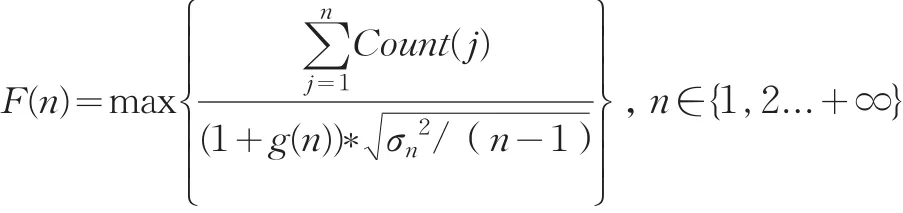
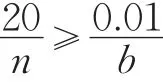
1.3 涨跌概率推断模型的构建

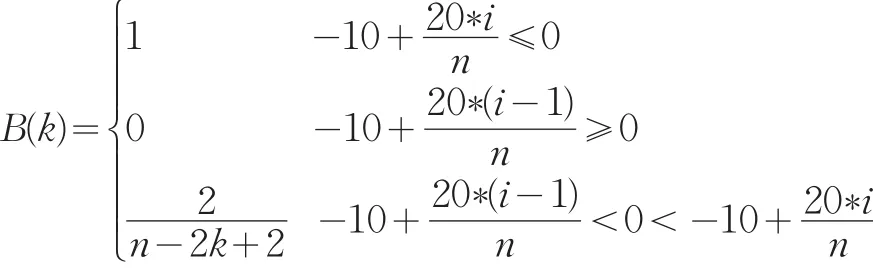
本文以{G(t+1)＞60%|G(t+1)＜40%}作为判别条件，当G(t+1)的值大于60%时，我们认为第t+1天股指上涨概率较大；当G(t+1)的值小于40%时，我们认为第t+1天股指下跌的概率较大。

2 股指涨跌概率推断模型的检验

2.1 股票指数与数据的选取

我们选取上证综合指数（000001），新上证综指（000017）以及深证新指数（399100）对股指涨跌概率推断模型进行检验。上证综合指数反映上海证券交易所上市的股票价格的总体趋势。新上证综指由沪市所有G股组成，股票在股权分置改革方案实施后的第二个交易日纳入指数，该指数与2006年1月4日发布。深证新指数上反映深圳证券交易所流通股票价格的变动情况，其以G股公司为主体编制，于2006年2月16日开始发布。

在对股指第t+1天涨跌情况进行推断时，采用的历史数据为2006年2月16日至第t天的数据。历史数据选取从2006年2月16日开始，是考虑到深圳新指数于2006年2月16日开始发布；另外在计量经济学中，一般认为时间序列里前期数据对后期数据的影响呈现一个递减的趋势，前期数据过多，反而使得数据预测会产生一个失真的效果，上证综合指数和新上证综指没有选取所有的历史数据进行拟合。从2006年2月16日以后的200个交易日后开始预测，因为如果前期数据过少，会导致集合S中缺乏的足够数据来进行泊松分布的拟合。总样本的数据截止于2011年6月30日，即进行预测的最后一天的数据为2011年6月30日。

2.2 模型的简化与模拟结果

本文采用Microsoft Visual Studio 2005 with C#进行编程，对股票指数涨跌概率进行估算。在本文前面建立的模型基础上，进行一定的简化处理。模型中需要遍历n={1→2000b}，但是在实际检验过程中，n取值范围简化为[15,50]。原因在于模型将收益率总区间进行了均匀分布处理，分区数不能过少，取n的下限值为15；在对部分数据进行处理后，发现n的取值一般在50以内，为了计算机处理的方便，我们取50作为上限值。

上证综合指数，新上证综指以及深证新指数的检验结果如表1所示。

表1 指数拟合结果

对上证综合指数而言，第一个符合 {G(t+1)＞60%||G(t+1)＜40%}的数值出现在2006年12月11日，由于本文为了使拟合的泊松分布接近真实值，故要求在对第一个数据进行拟合之前至少有200天的交易，而初始数据是从2006年2月16日开始，故第一个数据的出现接近2006年年底。n值取42时，拟合评估函数F(n)取得最大值。当n值为42时，该天上证综合指数收益率服从参数为23.67的泊松分布。根据股指涨跌概率推断模型，上证综合指数涨跌的概率G(t+1)为66.18%，上涨的概率比较高，而该天上证综合指数实际增长率为1.76%，推断正确。在所有符合{G(t+1)＞60%||G(t+1)＜40%}的日期里面，根据本文构建的模型判断上证综合指数涨跌与实际上证指数涨跌一致的占69.39%，说明该模型对上证综合指数涨跌的预测具有一定的准确性。

对新上证综指而言，第一个符合判别条件的数值出现在2006年12月11日。估计拟合函数F(n)取得最大值时，n值为18，该天收益率服从参数为12.33的泊松分布。根据股指收益率概率分布函数，判断该天新上证综指涨跌的概率G(t+1)为78.55%，上涨的概率高，而该天新上证综指实际增长率为1.85%，估计正确。在所有符合判别条件的日期里面，根据本文构建的模型判断新上证指数涨跌与实际涨跌相同的占到72%，说明该模型对新综指涨跌的预测具有一定的准确性。

对深证新指数而言，第一个符合 {G(t+1)＞60% ||G(t+1)＜40%}的数值出现在2006年12月11日，n值为21时，估计拟合函数F(n)取得最大值。该天服从参数为14的泊松分布，从而判断该天深证新指数涨跌的概率G(t+1)为78.21%，上涨的概率比较高，而该天深证新指数实际增长率为0.2%，估计正确。在符合判断条件的所有日期里面，根据模型判断深证新指数涨跌的概率与实际涨跌概率一致的占到64.2%，说明该模型对深证新指数涨跌的预测具有一定的准确性。

在选取的三种指数中，预测准确度最低的是深证新指数，为64.2%，但是其依然优于吕琦采用支持向量机的预测准确度63.3%，说明该方法是可取的。

3 结论

本文基于数据挖掘，构建了用于推断股指涨跌概率的新模型。通过对上证指数、新综指和深证新指数的实证检验表明该模型具有一定的准确性，其对新上证综指的拟合程度最好。但是该模型具有一定的缺点，判别条件的要求比较高，故并不能对每天的股指涨跌进行预测，有待进一步的改进。

[1]Cheol-Ho P,Scott H.Irwin.What do we Know about the Profitability of Technical Analysis?[J].Journal of Economic Surveys,2007,21(4).

[2]Kim K,Won B L.Stock Market Prediction Using Artificial Neural Networks with Optimal Feature Transformation[J].Neural Comput&Applic,2004,(13).

[3]Liu W，Zhang W.Stochastic Volatility Model and Technical Analysis of Stock Price[J].Acta Mathematica Sinica,English Series,2004,27(7).

[4]邓杰,唐国兴.中国股票市场技术交易规则有效性的实证分析[J].华东经济管理,2009,(5).

[5]李莎,李红刚.股票市场中技术分析有效性的实证研究[J].北京师范大学学报（自然科学版）,2009,(2).

[6]雷鸣,叶五一,缪柏其,郭文旌.生存分析与股指涨跌的概率判断[J].管理科学学报,2010,(4).

[7]吕琦.基于SVM的股票时间序列的预测研究[J].吉林工程技术师范学院学报,2009,(7).

[8]王志刚,曾勇,唐小我.中国股票市场技术分析非线性预测能力的实证检验[J].管理工程学报,2009,(1).