基于CRITIC的多属性决策组合赋权方法

张 玉，魏华波

（华北水利水电学院数学与信息科学学院，郑州 450000）

0 引言

多属性决策是多目标决策的一种,它是对具有多个属性的有限方案,按照某种决策准则进行多方案选择和排序。它的实际应用范围很广,包括社会、经济、管理等诸多领域。多属性决策问题的许多求解方法,一般都与属性权重有密切关系,因为权重的合理性直接影响着多属性决策排序的准确性,所以在多属性决策中,权重问题的研究占有重要地位。

目前确定权系数的方法有多种,大体上可分为主观赋权法和客观赋权法两大类[1]。主观赋权法是基于决策者给出的主观偏好信息或决策者直接根据经验给出的属性权重的。例如专家调查法、二项系数法、AHP法等。客观赋权法是基于决策矩阵信息,通过建立一定的数学模型计算出权重系数的。例如熵技术法,主成分分析法,多目标最优化方法等。两大类赋权方法各有不同的特点。主观赋权法可以体现决策者的经验判断,属性的相对重要程度一般不会违反人们的常识。但其随意性较大,决策准确性和可靠性稍差。客观赋权法存在赋权的客观标准,可利用一定的数学模型,通过计算得出属性的权重系数。其缺点是忽视了决策者的主观知识与经验等主观偏好信息,有时会出现权重系数不合理的现象。

为了使多属性决策的排序结果更科学,一种合理的做法就是将不同的赋权法所得的权重系数按照一定的方法进行组合。通过组合赋权,使排序结果既能体现主观信息,又能体现客观信息。文献[1],[2]分别提出了一种主、客观赋权集成方法,它们均通过建立一个数学规划模型来求解属性组合权重。目前优化组合赋权方法的研究还不完善,有必要进一步探讨多种准则下的优化组合赋权方法,并进行比较分析。一种新的基于CRITIC准则下的多属性决策的最优组合赋权方法。利用该方法对文献[1]的实例进行了计算,其结果与文献[1]的结果一致,表明本文提出的最优组合赋权方法的科学合理性。

1 基于CRITIC的多属性决策的组合赋权方法的基本原理

设有某个多属性决策问题,其方案集表示为S={S1, S2,...,Sm}其属性(或指标)集表示为P={P1,P2,...,Pn},第i个方案Si对第j个属性Pj的属性值记为aij,i=1,2,…, m,j=1,2,…,n,A=(aij)m×n称为属性矩阵或决策矩阵。通常,属性可分为效益型、成本型。所谓效益型属性是指属性值愈大愈好的指标,成本型属性是指属性值愈小愈好的指标。由于不同的属性往往具有不同的量纲和量纲单位,为了消除它们带来的不可公度性,在决策之前首先应将属性指标作无量纲化处理。然而,决策属性类型不同,无量纲化处理方法也将不同。对于效益型属性,一般可令：

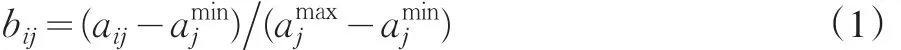
对于成本型属性，一般令 ：

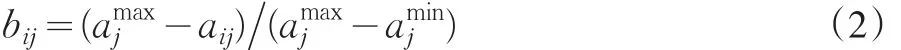
式中：

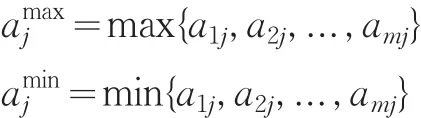
上述的无量纲化处理的矩阵B=(bij)m×n称为规范化的决策矩阵,bij表示第i个方案Si对第j个属性Pj的规范化属性值,矩阵B的第i行表示第i个方案Si对n个属性值的规范值。显然bij愈大愈好。

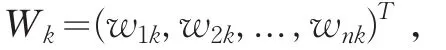
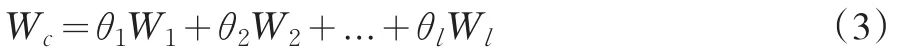
称Wc=(wc1,wc2,...,wcn)T为组合权系数向量。式中θ1,θ2,...,θl为组合权系数向量的线性表示系数。θk≥0 k=1,2,…,l,且满足约束条件:

各个指标的客观权重就是以对比强度和冲突性来综合衡量的。设Cj表示第j个评价指标所包含的信息量，则Cj可以表示为:

Cj越大，第j个评价指标所包含的信息量越大，该指标的相对重要性也就越大，所以第j个指标的客观权重：

2 组合赋权方法检验的探讨

组合赋权方法理论上可以综合集成主、客观信息,但是还有必要探讨运用多种组合赋权方法的前提条件及效果,即探讨组合赋权方法的检验问题[4]。组合赋权方法的事前检验主要用来印证主、客观赋权法的结果是否一致。这可以采用Kendall一致性系数检验法进行检验。如果l种具体的主、客赋权方法通过一致性检验,结果相差不大,此时考虑到计算上的简便性和信息的完备性,可以直接计算一种方法的算术平均[4],将其作为组合权系数:

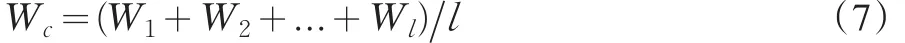
如果l种主、客赋权方法没有通过一致性检验,就可以通过本文提出的基于CRITIC的多属性决策的最优组合赋权向量的分析结果。为了反映本文提出的组合赋权方法与其它方法的合理性,同样有必要研究它的事后检验问题,可采用Spearman等级相关系数检验法[4]对组合赋权法进行事后检验。

综上所述,基于CRITIC法的多属性决策的最优组合赋权的计算步骤可归纳如下：

步骤1 由属性矩阵A=(aij)m×n,根据式(1)式(2)计算规范化的属性矩阵B=(bij)m×n

步骤2 采用Kendall一致性系数检验法对各种主、客赋权方法进行一致性检验,若通过检验,按式(7)计算组合赋权向量Wc,转步骤4。否则,转下一步;

步骤3 根据CRITIC法式（5）和式（6）计算出的θ={θ1,θ2,...,θl}再根据式(3)求出归一化的最优组合赋权向量Wc。

步骤4 利用所求的组合权重权重Wc进行多属性综合评价

步骤5 与其它方法一起进行组合赋权方法的事后检验,并作对比分析。

3 应用举例分析

下面以文献[1]中的例子的数据,运用上面提出的基于CRITIC法的多属性决策的最优组合赋权向量的分析结果。这是一个在市场上选择机器人的多属性决策问题。考虑到一个用户要选择机器人，其方案集为S={S1,S2,S3,S4}分别表示4个可供选择方案；其属性集P={P1,P2,P3,P4}即由4个属性，它们分别是:P1表示价格($10000)；P2表示速度(m/s)；P3表示可重复性(mm)；P4表示负载能力(kg)其中P1,P3为成本型属性，P2,P4为效益型属性。该问题的原始决策矩A=(aij)4×4

根据式（1）和（2）计算规范化属性矩阵B=(bij)4×4

假设第一类赋权方法为主观赋权法,机器人用户聘请3位专家给出关于属性的权重(文献[1])向量分别为：

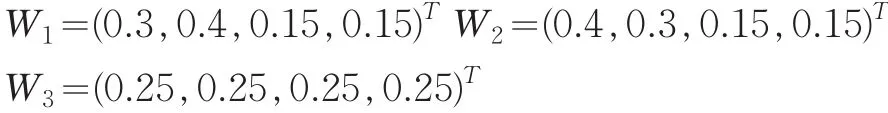
假设第二类赋权方法为客观赋权法,运用文献[1]给出的客观赋权法,可以求出4个属性的权重向量为：

上面的4种赋权方法权重向量表明各属性的排序有一定的差异,Kendall一致性系数检验的结果是4种赋权方法不具有一致性。

利用求得各个权重向量的相关系数矩阵为R：

各个权重向量的标准差为(σ)：

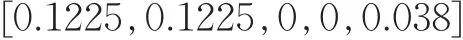
利用式（5）求得信息量(C)为：

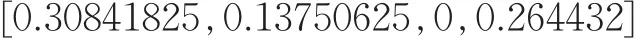
再根据式（6）求得权重系数θ={θ1,θ2,...,θl}：

根据（3）式求得组合权重:

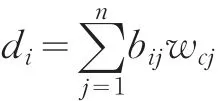
则可以计算每个方案的综合评价值为：

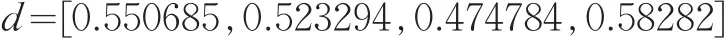
排序的结果为S4＞S1＞S2＞S3,“＞”表示优于。

文献[1]的最优组合赋权向量为Wc=[0.2733,0.2688, 0.2509,0.2100],可见本文提出的组合赋权方法和文献[1]方法对4种属性有相同的排序。因此对此市场上选择机器人的多属性决策问题,本文提出的方法所得的排序结果和文献[1]的结果是一致的。由文献[4]给出的Spearman等级相关系数计算式知,它们与原来的4种赋权方法之间具有相同的平均相关程度。实例说明了本文提出的以CRITIC法为准则的最优组合赋权方法的有效性。

4 结束语

在多属性决策中,权重问题的研究占有重要地位。因为权重的合理性直接影响着多属性决策排序的准确性。本文给出了基于CRITIC多属性决策的最优组合赋权方法,它综合了各种赋权方法的特点,可通过利用权重之间的对比强度和冲突性求出组合赋权系数。本文方法概念清楚、涵义明确,同时计算也不复杂。应用举例表明,本文方法排序结果准确。可操作性较强,具有重要的推广应用价值。

[1]樊治平,张全,马建.多属性决策中权重确定的一种集成方法[J].管理科学报,1998,1(3).

[2]樊治平,赵萱.多属性决策中权重确定的主客观赋权法[J].决策与决策支持系统,1997,7(4).

[3]D.Diakoulaki,G.Mavrotas，L.Papayannakis.Determaining Objective Weights in Multiple Crireria Paoblems:The CRITIC Method[J].Computer Ops.Res.22,1995.

[4]曾宪报.组合赋权法新探[J].预测,1997,16(5).