谐波平衡法在低速非定常流模拟中的应用

杜鹏程 宁方飞

(北京航空航天大学 能源与动力工程学院，北京 100191)

谐波平衡法在低速非定常流模拟中的应用

杜鹏程 宁方飞

(北京航空航天大学 能源与动力工程学院，北京 100191)

谐波平衡法是一种有效的周期性非定常流的计算方法.采用基于可压缩流的谐波平衡方程在计算低速不可压流动时，会由于对流通量计算格式中的数值粘性污染，降低解的精度和收敛性.采用预处理技术，使得基于可压缩流的谐波平衡方程可以直接用于低速周期性非定常流的计算中.选取典型的不可压方腔驱动流和低雷诺数圆柱绕流为例进行了时间推进法和谐波平衡法的计算对比.计算结果表明预处理后的谐波平衡方程适合于低速流的计算，在谐波平衡法中采用较少阶数的谐波计算就可以还原出几乎准确的非定常流场.

周期性非定常流;谐波平衡法;低速预处理;方腔驱动流;圆柱绕流

周期性非定常流是一种在内流、外流中常见的流动，如叶轮机的动静干涉、震荡叶栅、翼形的俯仰振荡等.对于这类问题的求解通常采用传统的时间推进法.基于时间推进法的非定常计算往往十分耗时，计算的大部分时间用于过渡到周期性状态的中间计算过程.为了减少计算时间，傅里叶方法被引入到上述周期性非定常流计算中［1］.在这类基于傅里叶方法的频域方法中，参考文献［2］提出的谐波平衡法将频域方程变换回时域求解，同时可以很方便的处理湍流模型问题，能在保证计算精度的同时，加快计算速度，从而得到了广泛关注和应用［3］.

在低速不可压流计算中，如果采用基于可压缩流动方程的计算格式，则会由于对流通量计算格式中的数值粘性过大和数值刚性问题造成解的精度降低且收敛性差［4］.因此不能将基于可压缩流的谐波平衡方程直接应用于低速周期性非定常流计算中.而时间预处理方法可有效地解决这一问题.该方法通过在可压流控制方程的时间导数项左乘一个预处理矩阵，改变了对流通量系数矩阵的特征值，降低了其系数矩阵的条件数，改善了数值刚性;并相应修改其对流通量格式中的耗散项，从而可根据流动条件减小数值粘性.当然，预处理矩阵形式并不唯一，选定不同的预处理矩阵可推导出不同对流格式的预处理形式.参考文献［5］对不同的预处理矩阵做了分析对比.

本文采用低速预处理，使得可以将基于可压缩流的谐波平衡方程直接用于低速周期性非定常流的计算中.并用方腔驱动流和低雷诺数圆柱绕流这两个基本算例进行了验证.

1 流动控制方程

1.1 时间推进法

采用有限体积法离散的Navier-Stokes方程可以写为

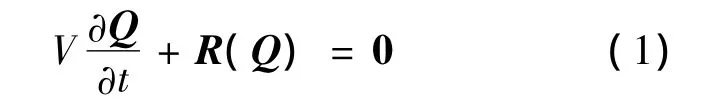
式中，Q 为守恒变量;Q=［ρ，ρu，ρv，ρw，ρE］T;V 为控制体的体积;R为残差向量.对于定常计算，本文采用隐式算法LU-SGS求解，即是求解:

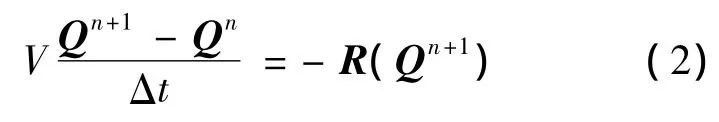
非定常计算采用双时间步方法DTS(Dual Time Stepping)推进求解如下方程:

式中，Δt*为物理时间步长.

1.2 谐波平衡法

作为时间推进法的一种降阶模型，谐波平衡法HB(Harmonic Balance method)可以计算时间周期性流动［2］.对于周期性流动，其解Q和残差R(Q)同样是时间的周期函数，频率为ω，可以将其用有限阶傅里叶级数近似表示为

将式(4)代入控制方程式(1)，利用正弦函数的正交性，对其进行谐波平衡，可得

式(5)为方程数和未知数都为NT=2NH+1个的方程组，写成矩阵形式为

由于控制方程式(6)在频域内的形式很复杂，直接计算十分麻烦.文献［2］巧妙的利用离散傅里叶变换将频域方程(6)再转化回时域中求解.取一个周期T=2π/ω内均匀分布的NT个时刻的解，定义:

其中Δt=T/NT，利用离散傅里叶变换，可得

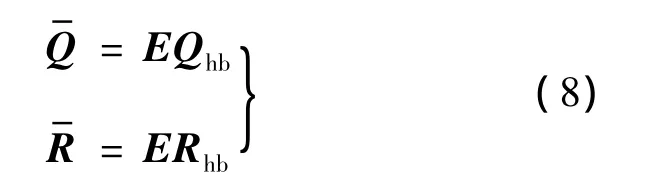
将式(8)带入式(6)可得

其中D=E－1AE.对于式(9)的求解，引入虚拟时间推进求解:

可以看到，谐波平衡法相当于是同时求解一个周期内NT个时刻的“定常”流场，并通过源项Shb将这NT个时刻的流场关联起来.但该源项的存在会影响计算的稳定性，使得计算可取的CFL数变小.本文谐波平衡方程的求解采用参考文献［6］提出的隐式BJ-SSOR算法.

1.3 带低速预处理的谐波平衡方程

谐波平衡法的控制方程(10)和控制方程(1)相比，其对流通量的求法不变.因此在计算低速流时采用基于压缩流动方程所发展的对流格式，则会由于数值粘性过大和数值刚性问题造成解的精度低且收敛性差.本文采用预处理方法来解决这一问题.预处理的基本原理和预处理矩阵的具体推导参见文献［5］，最终得到带预处理的谐波平衡方程为

其中

2 算例1——方腔驱动流

2.1 定常计算

方腔驱动流通常用来进行低速不可压流的计算验证［8］.即是一个长度为D的方腔，上壁面以速度U做匀速运动，其余壁面静止，由于流体的粘性，会在方腔内形成一个稳定的漩涡.本文取U=0.1m/s，保证雷诺数 Re=100，流动的马赫数约为 0.001.

在定常计算时，网格大小为均匀分布的41×41.不采用预处理时，由于数值粘性过大，使得方腔中的流体几乎静止.当选取预处理马赫数Mr=0.001后，计算得到的方腔中间截面的速度分布和参考文献［9］的计算结果吻合很好，如图1所示.同样，能准确计算得从右壁面－下壁面－左壁面的静压升系数分布，如图2所示.

2.2 非定常计算

使上壁面做周期性往复运动:

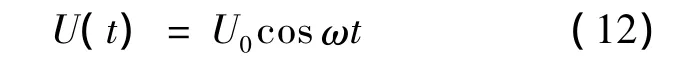
本文取ω=1 rad/s.双时间步非定常计算时一个周期内采用60个物理时间步，每个物理时间步内沿虚拟时间步推进求解30次，使其残差下降1×10－3量级.沿时间推进求解3个周期左右，流动就已达到良好的周期性状态，上壁面阻力系数随时间的变化过程如图3所示.

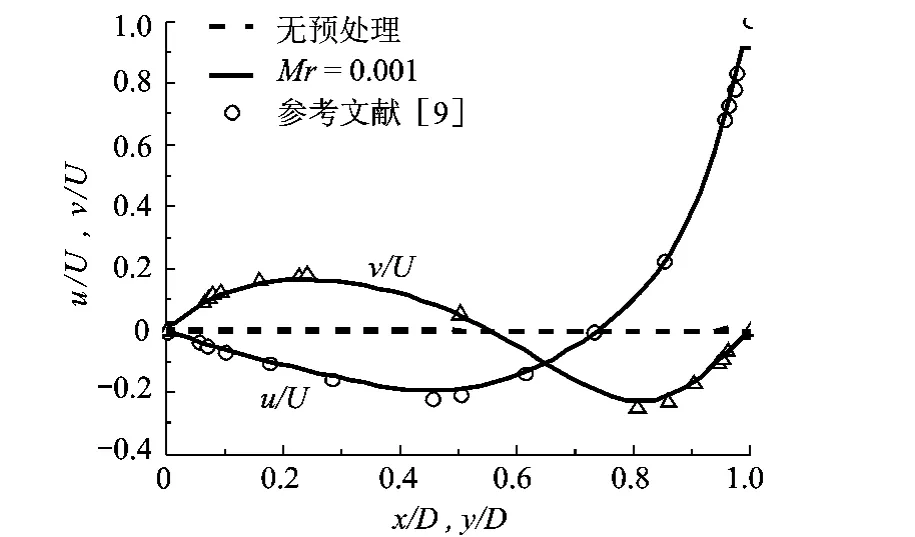
图1 方腔中间截面的速度分布

图2 沿壁面的静压升系数分布

图3 时间推进法计算的阻力系数随时间的变化

在谐波平衡法计算中分别采用了不同阶数谐波，并还原得到t=0.5T时刻的流场，方腔内的流线与时间推进法计算结果的对比如图4所示.虽然上壁面做一阶谐波非定常运动，但是由于流体控制方程的非线性，如果仅仅采用一阶谐波，还原得到的流场误差较大，该时刻涡的运动中心有明显区别，位置更加靠近中间截面.随着采取的谐波阶数的提高，还原得到的流场更加准确.采用3阶谐波，即计算7个时刻的流场，就可以很好的还原出该时刻的非定常流场.

计算得到的一个周期内上壁面的阻力系数的变化如图5所示.由于阻力系数的计算只涉及到靠近上壁面处的流场，采用1阶谐波就可以得到较准确的阻力系数的分布.当采用的谐波阶数N≥3后，再增加谐波的阶数对于解的精度没有明显的提高，并和时间推进法计算的阻力系数的幅值存在较小的差别.这是因为在对流通量和粘性通量这些非线性项计算时，采用有限阶的谐波截断和傅里叶变换总是抛弃了一些高阶项，存在一定的计算误差.

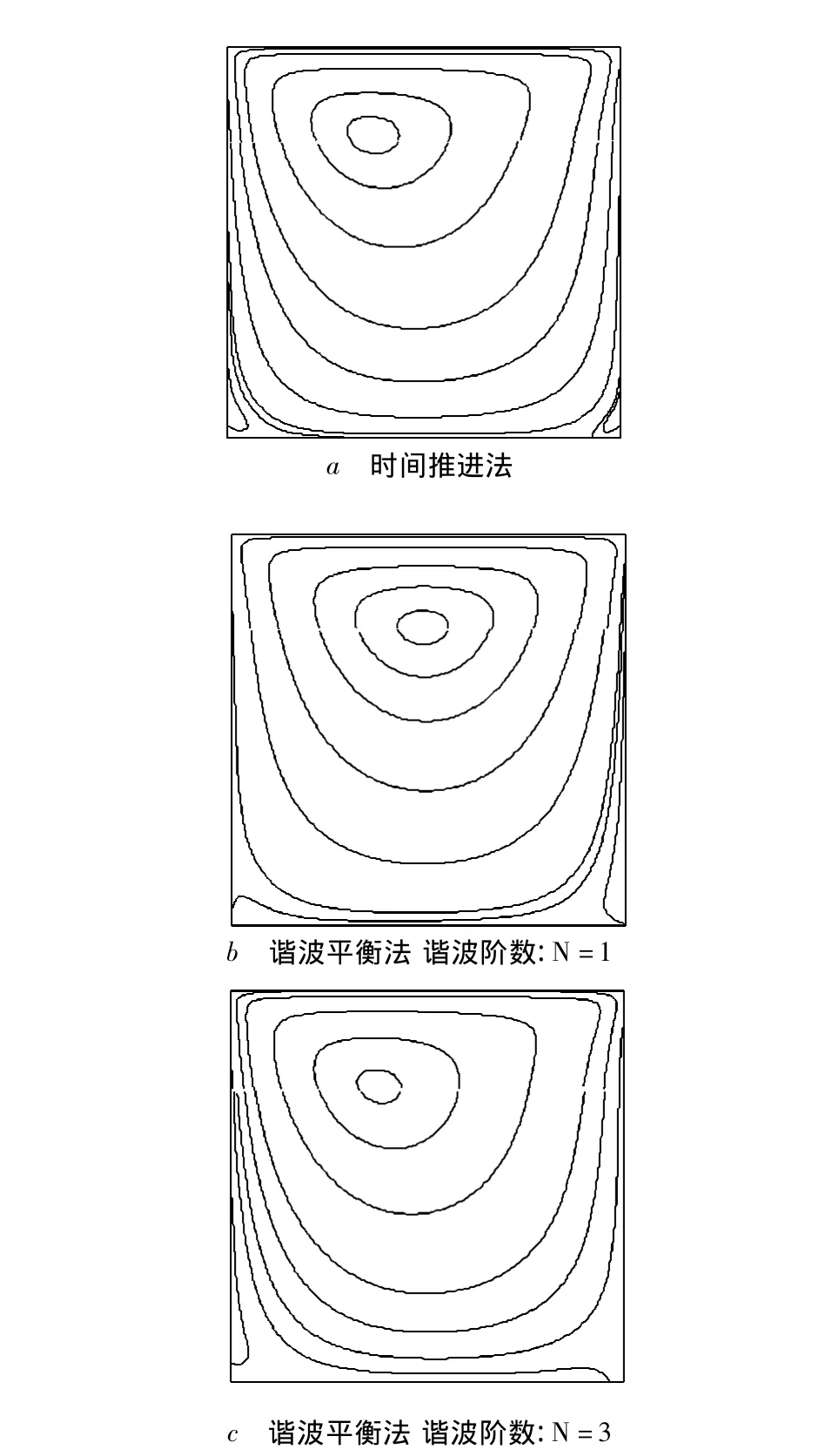
图4 t=0.5T时刻方腔内流线的对比

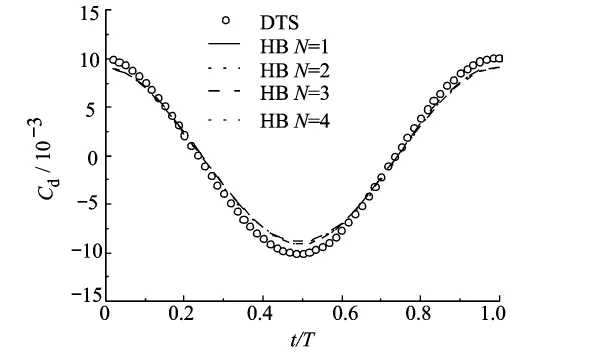
图5 一个周期内的阻力系数对比

3 算例2——低雷诺数圆柱绕流

3.1 定常计算

首先，以Re=41的定常圆柱绕流为例验证所采取的预处理方法.计算域为20倍圆柱直径，网格为91×81的简单O型网格，流动的马赫数为0.001.从图6可以看到不使用预处理时，耗散过强，流动没有分离;而采用预处理后，减少了对流格式的数值耗散，计算的流线和实验吻合很好，分离区的大小约为2倍圆柱直径.

图6 Re=41的低速圆柱绕流的流线图

3.2 非定常计算

当圆柱绕流的雷诺数增加到Re=200时，圆柱后就会出现周期性的涡的脱落，出现“卡门涡街”.首先采用非定常计算，预处理马赫数取为0.01，计算网格为156×156，其计算的阻力系数Cd和升力系数Cl随时间的演化过程如图7所示.计算得到的阻力系数 Cd=1.35±0.039，升力系数Cl= ±0.64，涡脱落频率(Strouhal数)St=0.19.本文的计算结果和其他研究者的计算或实验结果吻合很好，如表1所示.

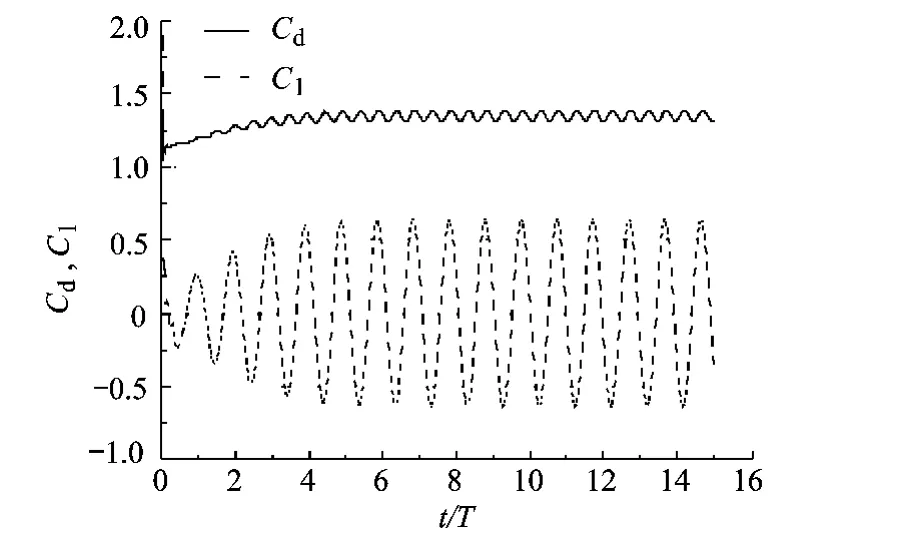
图7 阻力、升力系数随时间的变化

表1 Re=200的圆柱绕流的非定常计算结果对比

在采用谐波平衡法计算时，需要事先知道涡的脱落频率，或者采用参考文献［13］提出的一种基于梯度类的寻优算法来动态的决定涡的脱落频率.这里直接利用时间推进法计算得到的涡的脱落频率作为谐波平衡法中涡脱落的基准频率.

采用不同阶数谐波计算的阻力、升力系数如表2所示.随着所采取的谐波阶数的增加，阻力系数的均值保持在1.35左右，和时间推进计算结果基本一致;升力系数为±0.67，比时间推进计算结果略大，但在表1其他研究者计算的范围之内.

表2 不同阶谐波计算得到的阻力、升力系数

在谐波平衡法计算中，当采用较少阶数谐波时，计算误差大;采用更多谐波计算时，计算精度虽然会得到改善，但增加了计算时间和内存需求.为了分析实际需要的合理的谐波阶数，在圆柱后沿轴向选择4个监控点(A，B，C，D).利用时间推进法计算得到的一个周期内守恒变量ρu的变化规律如图8所示.可以看到在圆柱后涡交替脱落的A点，其在一个周期内的变化剧烈，需要采用较多阶数的谐波来分辨;而随着涡向下游的不断传递，由于粘性耗散，其ρu的变化趋于平缓，只需要较少阶数的谐波.这也可以从图9，这4个点ρu的傅里叶分析的频谱图中看出，在A点，其前6阶谐波的幅值和一阶谐波幅值相比，不可忽略，故需要大约6阶谐波才能较好的分辨出A点的非定常信号，而在B，C，D点需要的谐波阶数越来越少，在D点，只需3阶谐波即可.

图8 时间推进法计算的一个周期内监控点ρu的分布

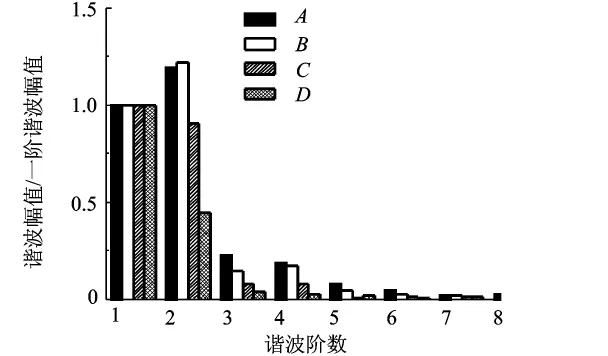
图9 时间推进法计算的监控点的ρu的频谱

图10为采用不同阶数谐波计算还原得到的t=0.5T时刻的流场和时间推进法计算流场的对比.采用一阶谐波，能够分辨出涡脱落的基本过程，但是分辨率很差.采用3阶谐波对C，D点附近的流场细节有很好的分辨能力，但对A，B点附近的流场分辨不够，这和图9的傅里叶分析结果匹配.当采用6阶谐波计算时，就可以很好的还原出整个涡脱落区的流场细节.

图10 t=0.5T时刻涡量的对比

上面的分析表明如果能够采用自适应的谐波平衡法，即是在流场变化大的区域采用较多阶数的谐波，在流场变化平缓的区域采用较少阶数的谐波，这样与全场采用同样多高阶谐波的计算相比，可以减少计算量和内存需求，这也是作者后续研究的方向之一.

4 结论

1)采用时间预处理方法，可以用基于可压缩流方程的计算格式求解低速不可压流，从而将高、低速流的计算在同一个方程中统一起来.

2)在低速周期性非定常流计算中，带预处理的谐波平衡方程可以采取较少阶数的谐波计算，还原得到一个周期内几乎准确的非定常流场.表明在计算规模大，采用时间推进法求解需要漫长的中间过渡态的周期性非定常流计算中，采用谐波平衡法，可以大大减少计算时间.

3)有必要进一步研究自适应的谐波平衡法，减少谐波平衡法的计算时间和内存需求.

References)

［1］ He L.Fourier methods for turbo machinery applications［J］.Progress in Aerospace Science，2010，46(8):329 －341

［2］ Hall K C，Thomas JP，Clark W S.Computation of unsteady nonlinear flows in cascadesusing a harmonic balance technique［J］.AIAA Journal，2002，40(5):879 －886

［3］ Lucia D J，Beran P S，Silva W A.Reduced-order modeling:new approaches for computational physics［J］.Progress in Aerospace Sciences，2004，40(1 －2):51 －117

［4］ Turkel E.Preconditioning techniques in computational fluid dynamics［J］.Annual Review of Fluid Mechanics，1999，31:385 －416

［5］ Briley W R，Taylor L K，Whitfield D L.High-resolution viscous flow simulations at arbitrary Mach number［J］.Journal of Computational Physics，2003，184:79 －105

［6］ Sicot F，Puigt G，Montagnac M.Block-Jacobi implicit algorithms for the time spectralmethod［J］.AIAA Journal，2008，46(12):3080－3089

［7］ Edwards JR.Towards unified CFD simulationsof real fluid flows［R］.AIAA-2001-2524，2001

［8］曹宁，吴颂平.低速流预处理Roe格式中的数值粘性［J］.北京航空航天大学学报，2010，36(8):904－908 Cao Ning，Wu Songping.Numerical dissipation of Roe's scheme with preconditioning for low-speed flows［J］.Journal of Beijing University of Aeronautics and Astronautics，2010，36(8):904 －908(in Chinese)

［9］ Ghia U，Ghia K N，Shin C T.High-Re solutions for incompressible flow using the Navier-Stokes equations and amultigridmethod［J］.Journal of Computational Physics，1982，48:387 － 411

［10］ Dyke Van，Milton D.An album of fluid motion［M］.Stanford，CA:Parabolic Press，1982

［11］ Chin Hoe Tai，Zhao Yong.Parallel unsteady incompressible viscous flow computations using an unstructured multigrid method［J］.Journal of Computational Physics，2003，192:277 － 311

［12］ Rosenfeld M，Kwak D，Vinokur M.A solution method for the unsteady and incompressible Navier-Stokes equations in generalized coordinate systems［R］.AIAA-88-0718，1988

［13］ McMullen M，Jameson A，Alonso JJ.Application of an on-linear frequency domain solver to the Euler and Navier Stokes equations［R］.AIAA 2002-0120，2002

(编 辑:张 嵘)

Application of harmonic balance method in simulations of low speed unsteady flows

Du Pengcheng Ning Fangfei
(School of Jet Propulsion，Beijing University of Aeronautics and Astronautics，Beijing 100191，China)

The harmonic balance method is an effective computational method in simulating time periodic unsteady flows.When using the harmonic balance method based on compressible flow equations to solve low Mach number flows，both the accuracy and convergence of the solution would be deteriorated due to the large dissipation of the convective scheme which is specially designed for compressible flows.To solve this problem，the low speed preconditioning was adopted;therefore，the harmonic balance method based on compressible flow equations could be used to compute low speed periodic unsteady flow directly.Both the time marching calculation and the harmonic balance calculation were performed in simulating the incompressible lid-driven flow and the low Reynolds number vortex shedding cylinder flow.The results show the capability of using the preconditioned harmonic balance equation in simulating low speed periodic unsteady flows，and the unsteady flowfield could be well reconstructed by using only a few harmonics retained in the harmonic balance method.

periodic unsteady flow;harmonic balance method;low speed preconditioning;lid-driven flow;cylinder flow

V 211.3

A

1001-5965(2012)06-0766-06

2011-03-16;网络出版时间:2012-06-15 15:44

www.cnki.net/kcms/detail/11.2625.V.20120615.1544.031.htm l

国家自然科学基金资助项目(50506001)

杜鹏程(1986－)，男，四川宣汉人，博士生，dupengcheng22@163.com.