单星导航HEO卫星初轨确定算法

李涛护 刘建胜 秦红磊 李 锐

(北京航空航天大学 电子信息工程学院，北京 100191)

单星导航HEO卫星初轨确定算法

李涛护 刘建胜 秦红磊 李 锐

(北京航空航天大学 电子信息工程学院，北京 100191)

HEO(Highly Elliptical Orbit)轨道卫星利用星载GPS(Global Positioning System)进行自主定轨面临的主要难题之一就是解决在单颗导航卫星条件下的初轨确定问题.从理论上分析了利用单颗导航卫星的观测量确定HEO卫星轨道初值的所需满足的条件，指出了利用F.G级数法求解初值存在的问题，提出了一种基于轨道根数约束的迭代批处理算法，该算法无需复杂的数学运算，避免了F.G级数法用短弧资料定初轨时系数矩阵秩亏的影响.仿真结果表明，当先验轨道根数误差在允许范围内取值时，在考虑轨道射入误差的情况下，初值的位置偏差在104m量级，速度偏差在100m/s量级，能够根据单颗导航卫星的短弧观测值可靠地完成轨道初值的确定.

HEO;初轨确定;自主定轨;GPS

自主定轨技术不仅能够提高卫星的自主能力，还能够减轻地面监控站的任务量，降低运行成本.当前，基于星载 GPS(Global Positioning System)的自主定轨系统已在低轨道卫星上得到了广泛应用，这在很大程度上归功于GPS为低轨道卫星提供了连续跟踪和多方位的观测几何.但对于大椭圆轨道(HEO，Highly Elliptical Orbits)卫星，由于其轨道高度往往高于GPS卫星，星载GPS接收机只能接收来自地球另一侧的导航信号，导致能够观测的导航卫星数目较少甚至是没有，此时将面临观测数据缺失的情况［1－2］.在高性能时钟的支持下，若采用动力学方程和测量方程结合的定轨方法，并利用高精度轨道模型作为状态方程，则仍可以对HEO卫星进行自主定轨［3］.

卫星轨道确定的过程实际上是通过求解轨道方程而对轨道初值不断改进的过程.若轨道初值偏差较大，则定轨滤波器可能会发散或者收敛到错误的状态.卡尔曼滤波需要轨道状态初值来启动递推算法，而偏差较小的初值可以提高滤波器的收敛速度，减少迭代次数，提高定轨性能.

由于受轨道类型、测站数目和观测资料等多种因素的影响，初轨计算有多种方法.比较有影响的方法有 Laplace方法、gauss方法、几何法［4］等.Laplace法和gauss法一般更适用于测角、测角+测距和点位资料［5］，不适用于星载GPS定轨.几何法适用于星载GPS产生的伪距+伪距变化率观测资料，但要求能接收4颗以上卫星，难以适用于可见导航卫星较少的环境.文献［6］研究了以两颗GPS卫星的观测量求解初值的过程，其具体方法为通过F.G级数法求解线性方程组，这种方法在观测量较少时易出现系数矩阵秩亏现象，而观测量较多时则计算量显著增大，同时两颗导航卫星的观测量也约束了在大椭圆轨道的应用.而在HEO卫星自主定轨系统中，大部分轨道区间上可见的导航星数目较少甚至没有，因此需要能够利用较少数目卫星的观测数据完成轨道初值的确定，现有的轨道初轨确定算法难以适应这种场景.在这种背景下，本文先从理论上分析了用单颗导航卫星的观测量进行初值确定的所需满足的条件，指出了F.G级数法存在的问题，然后提出了一种根据单颗卫星观测数据进行初值搜索的迭代批处理算法，无需复杂计算，适应较多观测数据的情况，能够很好地满足工程要求.

1 单星观测量初值确定分析

HEO卫星自主定轨采用的是动力学方程结合测量方程的定轨方法，以伪距和伪距变化率作为观测量，采用EKF(External Kalman Filter)作为导航滤波器进行自主定轨，EKF的状态量为ECI(Earth Centered Inertial)坐标系下的位置、速度以及钟差和频差共8个参数.定轨计算的基础是2个方程:卫星运动方程和测量方程.

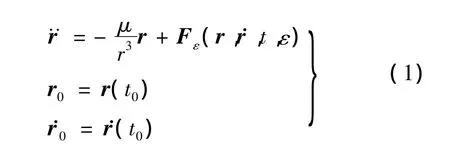
在ECI坐标系中，卫星相对于地心的运动方程为其中，r为卫星的位置矢量，表示摄动加速度，初轨计算即是通过观测量确定r0和r·0的过程.

测量方程给出卫星之间、星地之间的对应几何关系，如图1所示，其中S表示HEO卫星，S1表示导航卫星.

图1 测量方程几何关系

容易看出，卫星之间满足以下几何关系:

其中，ρ为观测量;R为导航卫星位置矢量.

在某一固定时刻，当只有一颗导航卫星时，根据观测量(伪距+伪距变化率)能够建立2个方程，但需要求解8个未知参数，观测量是不够的.但卫星轨道遵循的严格的动力学条件，即任意时刻的位置和速度都能够用初始时刻的位置和速度表示，常见的表示方法有F.G级数法和数值积分法.下式给出了无摄运动时F.G级数法描述的任意时刻卫星状态和初始状态之间的关系，有摄运动的表达式详见文献［7］.将多于8个时刻的测量值对应的几何关系引入后，结合式(3)，即可使方程个数多于未知变量的个数，使求解状态初值成为可能.

其中，F，G 和 F'，G'分别表示 ri和对的幂级数展开式.

尽管方程数目容易满足，但是对短弧测量数据，由于星间相对运动较平缓，相应的系数矩阵容易秩亏或接近秩亏状态，此时难以确定该方程组是否可解.为了从理论上研究能否根据单颗GPS观测量确定轨道初值的问题，可以建立自主定轨的非线性方程，然后通过分析该方程的可观测性进行研究.将定轨问题描述为自治非线性系统:

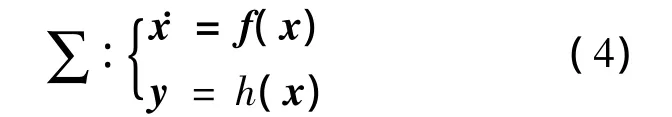
式中，x∈Rn为系统状态矢量;y为观测量;f，h分别表示卫星动力学方程和测量方程.该非线性系统可观测意味着在时间区间(0，t)内，系统输出的观测量能够提供足够的信息以确定系统的初始状态，即求解出正确的初值，因此可将初值求解问题转化为分析非线性系统的可观测性问题.根据轨道动力学理论，卫星运动状态并不完全在状态空间Rn上取值，而是在Rn的某些开子集或流形(如球面、环面)上变化，这种情况下，可以把系统置于流形上进行分析，认为非线性系统的动态特性是由定义在流形上的向量场决定的，根据非线性系统微分几何理论［8］，非线性方程可观测的条件是观测矩阵为满秩矩阵.

定义观测矩阵为

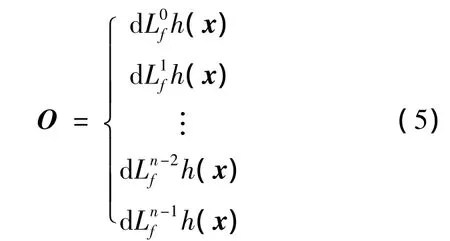
出于以上原因，本文基于批处理的思想，提出了一种迭代搜索算法，该算法无需复杂的运算，并可以用较短弧段的数据可靠地搜索出轨道初值，适于实际的应用.

2 迭代批处理算法

2.1 算法原理

由于摄动力的影响，在轨卫星实际运行轨道平面是随时间变化的近似椭圆轨道，轨道根数不再是常数，但由于摄动力是微小量，除平近点角τp外，其它根数(a，e，i，Ω，ω)仍可近似为常量，故可以根据轨道根数的前5个元素建立一个预计轨道，对状态量初值搜索的过程即转化为在预计轨道上对平近点角的确定过程.当星载接收机完成对GPS卫星的捕获和跟踪后，即可通过导航电文获取导航卫星的星历，从而得到卫星的位置和速度，结合接收到的观测值，即可对平近点角的真实位置进行搜索，当参与批处理的目标卫星时间序列与真实位置吻合或偏差较小时，观测量残差序列具有最小均方根值.

2.2 迭代搜索过程

在迭代搜索之前，首先要确定目标卫星进行批处理的数据序列时间间隔，一般数据序列的时间间隔与滤波器观测值时间间隔相同，记作d.为了便于说明，设j表示目标卫星时间序列的索引，m表示搜索起始点位置的索引，k表示迭代次数的索引.详细过程如下:

1)选择搜索起点，根据Kepler轨道模型生成一个轨道周期的时间序列，记作SHEO，序列长度为M;

2)确定批处理序列的长度，即在SHEO中选择一定长度的序列用于批处理计算，较长的数据序列能够取得更高的性能，但运算量也随之增大，故可在性能和计算能力两方面折中，设用于批处理的序列长度为N;

3)当前迭代次数为 k，k=1，2，…;

4)从SHEO序列的起始点开始搜索，即m=1，m=1，2，…，M;

5)将轨道根数转换成状态量:

6)然后计算批处理时间序列中的所有点和各自对应时刻的导航卫星的状态量之间的伪距估计值和伪距变化率估计值:

7)计算伪距估计值和伪距变化率估计值与真实观测量之间的残差序列:

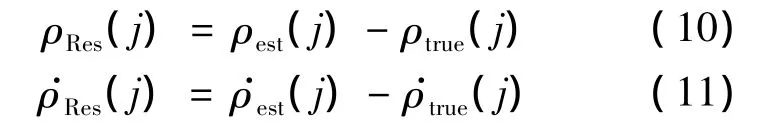
8)计算差值序列的累加均方根值;

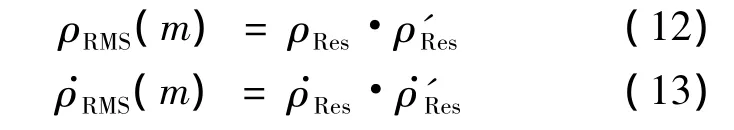
9)若m＜M，m=m+1，重复4)～8);

10)当m=M时，完成了一次迭代，将ρRMS和ρ·

3 仿真算例

下面以HEO卫星AMSAT OSCAR-40(AO-40)为例通过仿真算例说明算法的性能.AO40世界无线电爱好者卫星组织在2001年发射的HEO卫星，星上安装了高性能GPS接收机用于星载自主定轨的实验，其基本轨道参数为:轨道半长轴a=36286 km，轨道偏心率e=0.769 8;轨道倾角i=6.04°;轨道周期 T=19.1 h;近地点高度和远地点高度分别为1000 km和58800 km.

3.1 仿真数据产生

由两行式轨道数据格式(TLE，Two-Line orbital Element set format)文件得到目标卫星和GPS导航卫星的卫星初始星历，指定时间间隔的真实星历通过高精度轨道外推产生，考虑的摄动力模型为:30×30阶的JGM-3重力场模型、日月三体摄动;相对论摄动;固体潮汐摄动(太阳和月亮);固定面值比太阳辐射压摄动，采用RKF45积分滤波器.计算GPS与HEO卫星之间的距离值和伪距变化率值，并将此值加上噪声后作为滤波器的观测量.

轨道初值所在的轨道平面不考虑摄动力的影响，根据二体模型用卫星轨道的前5个轨道根数生成一个完整周期的轨道采样点，轨道间隔与观测数据接收间隔相同.

3.2 仿真参数设置

目标卫星轨道根数来自于TLE星历文件，比较了在有无轨道射入误差情况下的算法处理结果.轨道射入误差设置为:

近地点高度附件误差:1 km

远地点高度附近误差:100 km

轨道倾角误差:1°

升交点赤经误差:1°

仿真起始时刻设为UTC2003年7月17日15:44:24，测量值接收间隔为1 s，则单个HEO轨道周期的轨道点数为1147;观测噪声为高斯白噪声，伪距和多普勒观测值方差分别为100 m和1m.观测数据起始点在远地点、近地点与两者之间各选择一个，分别为811，237，400，以检验算法在目标卫星不同轨道弧段所能取得的精度.批处理数据长度分别为50，200，500min.

4 仿真结果分析

图2给出了当观测数据起始点为811时利用迭代批处理算法以不同的批处理长度对AO40卫星进行初始状态量搜索得到的结果.横坐标表示目标卫星一个完整轨道周期的数据序列索引，尖峰所对的索引表示测量值起始点对应的目标卫星真实坐标在整个轨道周期中的位置，纵坐标表示参加批处理的数据序列经过算法处理后得出的残差累加均方根值.容易看出，数据长度较长的数据块峰值更尖锐，因此能更准确地确定搜索的位置，但用短弧数据也能很容易地搜索出真实位置，且不影响精度.观测数据起始点在其它位置时所得的图相似.

图2 不同长度数据算法处理结果

表1给出了不考虑射入误差时采用迭代批处理算法因不同的迭代间隔内进行搜索的性能.表中结果主要反映出算法的3个特点:①迭代时间间隔越小，状态量初始值与真实状态量之间越接近;②在不考虑射入误差的条件下，即轨道根数能比较准确地反应真实轨道，则所得的状态量初始值与真实值之间差距较小，此时滤波器能够较迅速收敛;③在目标卫星轨道的不同位置，所得的状态量初始值与真实值差值不同，且表现为近地点偏差最大，远地点偏差最小，其原因在于预计轨道和真实轨道在不同位置偏差量不同.

表2给出了在有射入误差条件下算法的搜索性能.搜索结果也体现出了与表1结果相似的特点，但不同的是，由于轨道根数存在误差，使得初始值与真实值之间的偏差较表1结果明显增大，可见预计轨道的精度对搜索结果的误差有着直接影响.当迭代间隔为0.01 s时，位置偏差量为104m量级，速度偏差量为米/秒量级，能够满足自主定轨滤波器的需求.

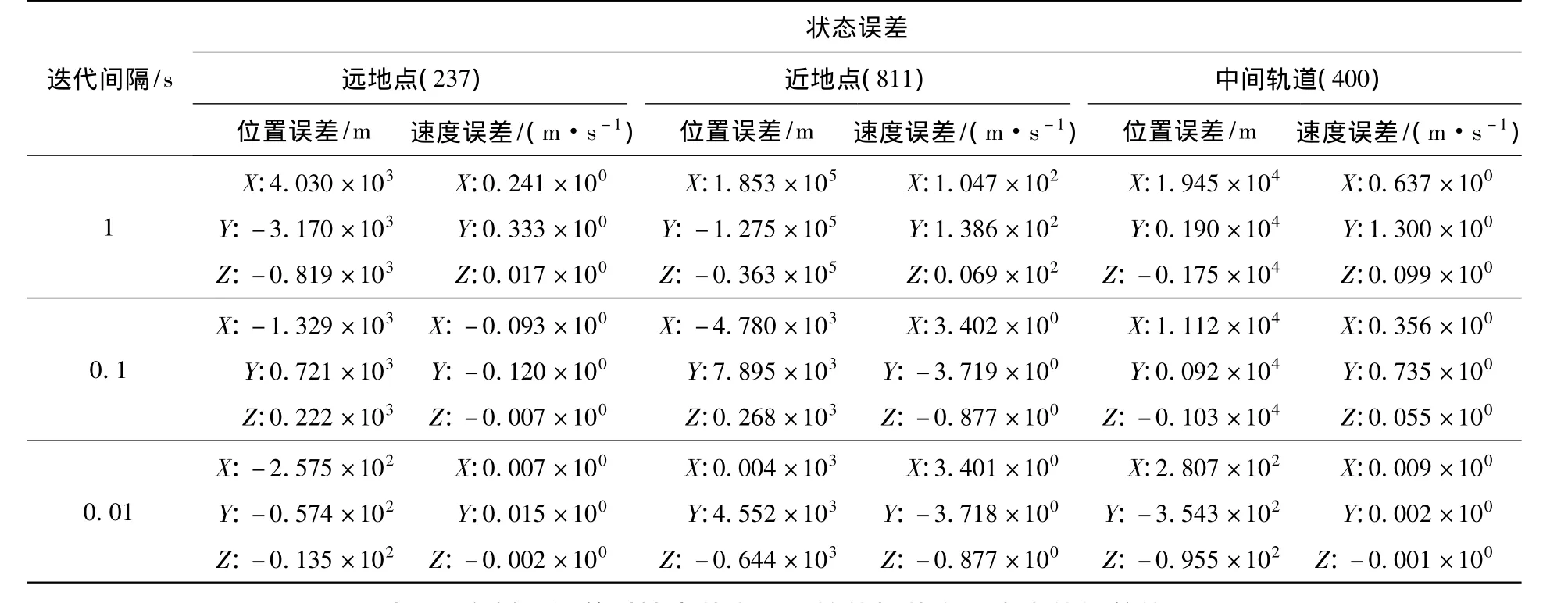
表1 无射入误差时搜索状态量初始值与真实状态量的差值

表2 有射入误差时搜索状态量初始值与状态量真实值的差值

5 结束语

基于星载GPS的HEO卫星自主定轨系统中，当可见卫星数目无法满足几何法求解条件时，导航滤波器的状态量初始值难以确定.本文以只能接收到一颗导航卫星为研究背景，提出一种迭代批处理法轨道的初值估计.本算法将已知的轨道根数作为先验信息，通过迭代查找对目标卫星在预计轨道的位置进行估计，能够有效地获取目标卫星的初值.需要指出，初值估计的准确度受限于预计轨道的精度，如果轨道根数能较准确地反映真实轨道的状态，则预计轨道与真实轨道之间的偏差可以足够小.通过仿真模型对算法性能进行了验证，结果表明，在导航卫星数目不足的环境中，即使只能接收到单颗导航卫星，只要鲜艳轨道根数能够满足一定的精度范围，迭代批处理法能够有效地确定滤波器值，使导航滤波器满足正常运行的条件，克服了传统方法难以解决的难题.

References)

［1］ Balbach O，Eissfeller B，HEIN GW，et al.Tracking GPS above GPS satellite altitude:first results of the GPS experiment on the HEOmission equator-S［C］//Proceedings of the 11th International Technical Meeting of the Satellite Division of the Institute of Navigation(ION GPS 1998).Nashville，TN:［s.n.］，1998:1555－1564

［2］ Davis G，Moreau M，Bauer F，et al.GPS-based navigation and orbit determination for AMSATAO-40 satellite［C］//AIAA Guidance，Navigation，and Control Conference and Exhibit.Monterey，California:AIAA，2002:5 －8

［3］ Long A，Kelbel D，Lee T，et al.Autonomous navigation improvements for high-earth orbiters using GPS［C］//Proceedings of the 15th International Symposium on Spaceceflight Dynamics.Biarritz:CNES，2000

［4］赵春梅，瞿锋.无准确初轨信息时星载GPS低轨卫星定轨方法研究［J］.测绘科学，2006，31(3):23 －27 Zhao Chunmei，Qu Feng.Research on methods of low-earth satellites orbit determination based on GPS without accurate preliminary orbit position［J］.Science of Surveying and Mapping，2006，31(3):23－27(in Chinese)

［5］刘林，张巍.关于各种类型数据的初轨计算方法［J］.飞行器测控学报，2009，28(3):70 －76 Liu Lin，Zhang Wei.Initial orbit determination for different data types［J］.Journal of Spacecraft TT＆C Technology，2009，28(3):70－76(in Chinese)

［6］刘艳芳，巨涛.用两颗GPS卫星确定低轨卫星轨道的初值方法［J］.中国空间科学技术，1999，4(2):47 －52 Liu Yanfang，Ju Tao.Initial value method of orbit determination using two GPS satellites［J］.Chinese Space Science and Technology，1999，4(2):47 －52(in Chinese)

［7］刘林.人造地球卫星轨道力学［M］.北京:高等教育出版社，1992:49－54 Liu Lin.Orbital dynamics of manned satellite［M］.Beijing:Higher Education Press，1992:49 －54(in Chinese)

［8］刘小河.非线性系统分析与控制引论［M］.北京:清华大学出版社，2008:235－240 Liu Xiaohe.Analysis and control of nonlinear systems［M］.Beijing:Tsinghua University Publishing House，2008:235 － 240(in Chinese)

［9］ Yim Jo R，Crassidis John L，Junkins John L.Autonomous orbit navigation of interplanetary spacecraft［R］.AIAA-2000-3936，2000

［10］ Alfriend K T，Dasenbrock R R，Kaufman B，et al.Autonomous interplanetary orbit determination using satellite-to-satellite tracking［J］.Journal of Guidance，Control，and Dynamics ，2007，30(3):679 －686

［11］ Lee Deok-Jin，Alfriend Kyle T ，OZA D H，et al.Landsat-4(TDRSS-user)orbitdetermination using batch least-squares and sequential methods［C］//AIAA/AAS Astrodynamics Conference.South Carolina:AIAA，1992:10 －12

［12］ Teixeira B O S，Bernstein D S，Santillo M A，et al.Spacecraft tracking using sampled-data Kalman filters［J］.IEEE Control Systems Magazine，2008，28(4):78 －94

(编 辑:娄 嘉)

Preliminary orbit determination method of HEO satellite using a single navigation GPS satellite measurements

Li Taohu Liu Jiansheng Qin Honglei Li Rui

(School of Electronics and Information Engineering，Beijing University of Aeronautics and Astronautics，Beijing100191，China)

The autonomous navigation of highly elliptical orbit(HEO)satellites using GPS needed to solve a key problem of the preliminary orbit determination under the condition of only one navigation satellite.The feasibility by using the pseudo-range

from a single navigation satellite was demonstrated，and the limitation of the F.Gmethod for preliminary orbit determination was figured out.An iterative batch method using orbit elements as constrains was proposed to determine the preliminary orbit.This algorithm did not have complex mathematic operation and could avoid the influence of ill-conditioned equation with short arc data by using F.Gmethod.The simulation results show that its positioning bias is about104m and velocity bias is approximate 100m/swith an acceptable orbit injection errors，and the proposed method using a single navigation satellite measurements could determine the HEO initial orbit credibly.

highly elliptical orbit;preliminary orbit determination;autonomous orbit determination;global positioning system

P 135

A

1001-5965(2012)06-0755-05

2011-04-02;网络出版时间:2012-06-15 15:44

www.cnki.net/kcms/detail/11.2625.V.20120615.1544.039.htm l

国家973资助项目(2010CB731805);国家自然科学基金资助项目(60902055)

李涛护(1976－)，男，安徽宿州人，博士生，thlee100@126.com.