独立多细节结构耐久性试验寿命的统计标定

贺小帆 董彦民 刘彦毛 刘文珽

(北京航空航天大学 航空科学与工程学院，北京 100191)

独立多细节结构耐久性试验寿命的统计标定

贺小帆 董彦民 刘彦毛 刘文珽

(北京航空航天大学 航空科学与工程学院，北京 100191)

在进行疲劳试验评定结构寿命时，为了能真实模拟实际结构形式和传载情况，模拟试件往往设计成多细节试件，进行不完全疲劳寿命试验，必须由多细节试件寿命推断单细节寿命.针对工程上常用的两种寿命分布形式:对数正态分布和双参数Weibull分布，以结构串联失效模型为基础，建立了由相同独立多细节结构疲劳寿命分布确定单细节寿命分布的统计标定方法.当多细节试件寿命服从对数正态分布时，可近似认为单细节寿命也服从对数正态分布，单细节寿命分布参数与多细节试件寿命分布参数间存在确定关系，并且单细节寿命数学期望和标准差均高于多细节试件相应参数;当多细节寿命服从双参数Weibull分布时，单细节寿命也服从双参数Weibull分布，其斜率不变，但位置参数按比例放大.最后给出了一个分析实例.

疲劳;使用寿命;多细节;对数正态分布;Weibull分布;统计标定

疲劳试验是验证和评定飞机结构耐久性的必需手段，在飞机结构的设计和使用阶段，要进行大量模拟试件的疲劳试验以获取疲劳特性参数，为结构设计和寿命评定提供依据.

飞机上存在大量的由独立相似细节构成的结构，在进行疲劳试验测试结构的寿命时，由于时间和经费限制，往往不可能进行成组的全尺寸疲劳试验，而是模拟结构细节进行元件级疲劳试验，此时就存在着考虑细节数量的元件寿命和结构寿命间的折算问题［1］，需要测试得到单个细节的疲劳寿命.但在元件级试验中，模拟试件一方面要能良好地模拟结构形式(如材料、连接状态、几何形状、尺寸)、表面状态和受力模式，另一方面又力求简单，能够实现以最简单的形式再现结构关键部位的力学特性，并易于疲劳试验.由于结构形式和功能要求，模拟试件往往含有多个细节.以飞机上最常见的连接件为例，为了实现合理的载荷传递和应力分布，模拟试件往往设计成对称的多孔叠层连接试件.此时，一旦一个孔破坏，则试件破坏，但是试件寿命反映的并不是单一细节的寿命，在评定含有多个细节的结构寿命时，以不完全疲劳试验寿命作为统计量来描述单细节的寿命会丧失部分信息，得到的结果过于保守.为了避免上述问题，在试验方面，进行了很多改进，如串联多细节试件，在一个细节破坏后，还可以将剩余部分继续试验以获得有效寿命信息，但是，这样加大了试件设计、加工以及疲劳试验的复杂性，工程上难以采用.

为了解决试验寿命的有效信息问题，本文讨论一种统计标定方法，即考虑试件细节数目对试件寿命进行推断以获取单细节寿命分布参数.

1 统计标定的含义和理论基础

1.1 假 设

1)细节相互独立，细节裂纹尺寸达到工程可检尺寸即认为细节失效，此时由于裂纹尺寸较小，不会引起其他细节的应力场变化，可以认为细节是相互独立的;

2)［n］个细节失效，则结构失效，并通常取［n］=1;

3)细节寿命分布形式相同;

4)多细节寿命可用对数正态分布或双参数Weibull分布描述.

1.2 统计标定的含义

多细节试件疲劳试验无法进行到所有细节失效，一旦部分细节失效则停止试验，属于不完全寿命试验，由多细节试件寿命分布和特征值推断单细节寿命分布和特征值的过程称为标定［2］.具体描述形式如下:设多细节寿命的概率密度函数为f(θ1)，单细节寿命的概率密度函数为 g(θ2)，其中f(x)，g(x)为分布函数，θ1和 θ2是分布参数.当f(θ1)已知，确定g(x)和θ2的过程称为统计标定，θ1和θ2是一种概率意义上的统计关系.

1.3 统计标定的理论基础

1)失效准则.对含M个独立细节的结构，假定其中［n］个细节失效，则结构失效.

以Y表示多细节结构的寿命，FY(N)=P{Y＜N}表示Y的分布函数.以X表示单细节寿命，FX(N)=P{X＜N}表示X的分布函数，则

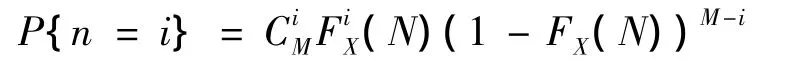
若令［n］=1，则多细节结构为串联结构，有

2)疲劳寿命分布特性

由于材料、几何、结构、加工等的分散导致的结构固有分散，疲劳寿命为随机变量，通常采用对数正态分布或Weibull分布描述疲劳寿命的分布特性［3］.其概率密度函数为

① 对数正态分布(LN，Log-Normal).包括最小值为0和最小值不为0的对数正态分布形式，其概率密度函数为

式中，N0为最小寿命;μ=E(lg(N－N0))为数学期望;σ为标准差.

② Weibull分布.包括三参数Weibull分布和双参数Weibull分布，其分布函数为

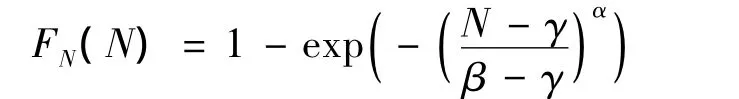
式中，γ为最小寿命;α为斜率;β为位置参数.

它由Weibull提出，基于最弱环理论，认为结构由若干个相同单元串联构成，最小单元的寿命决定了结构的寿命，其最佳极值分布为Weibull分布［4］.目前在军用运输机和民用飞机结构疲劳失效寿命分布特性中得到了广泛应用.

由于三参数分布参数多，参数估计稳定性差，工程上普遍采用最小寿命为0的对数正态分布和Weibull分布，以给出偏于保守的结果.

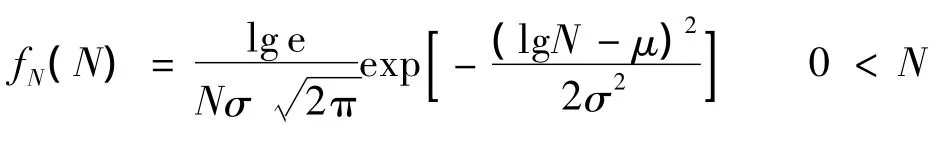
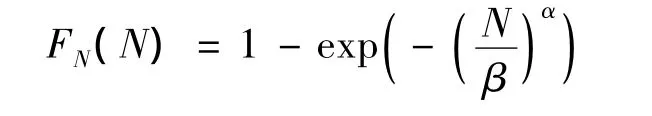
针对这两种分布形式，给出了常用金属结构的对数疲劳寿命标准差和双参数Weibull分布的斜率参数［5－11］.

2 基于Weibull分布的统计标定

假设相同多细节结构寿命服从双参数Weibull分布，取［n］=1，多细节结构寿命分布满足

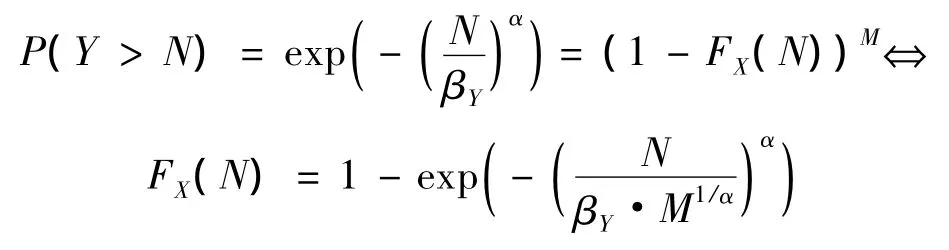
显然，单细节寿命X也服从双参数Weibull分布，且αi=α.表明单细节寿命分布斜率不变，而位置特征值是比例放大，设放大系数为 K，则K=M1/α，与细节数和分布斜率有关.

该问题属于典型的尺度效应问题，在Weibull及后续的文章中进行了大量的讨论［4］.

3 基于对数正态分布的统计标定

3.1 寿命分布及参数特性

取［n］=1，假定相同多细节结构寿命服从对数正态分布 LN(μ，σ2)，则有 Y=min{Xi|i=1，2，…，M}，转化为对数形式 Y'=lg Y=min{X'=lg Xi|i=1，2，…，M}

由于Y″为标准正态分布和X″的分布仅仅与M有关，记其数学期望和方差分别为 E(X″)和Var(X″)，用Mathcad软件计算得到的典型值见表1，且有

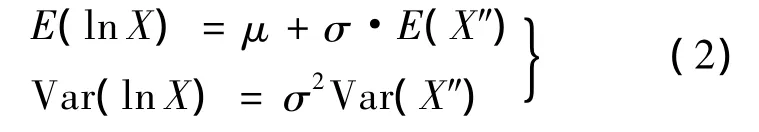
3.2 统计标定的近似方法

式(1)比较复杂，为便于应用，提出如下假设:

当多细节寿命Y服从对数正态分布时，单细节寿命X也服从对数正态分布.该假设等同于X″服从正态分布.

1)拟合优度检验

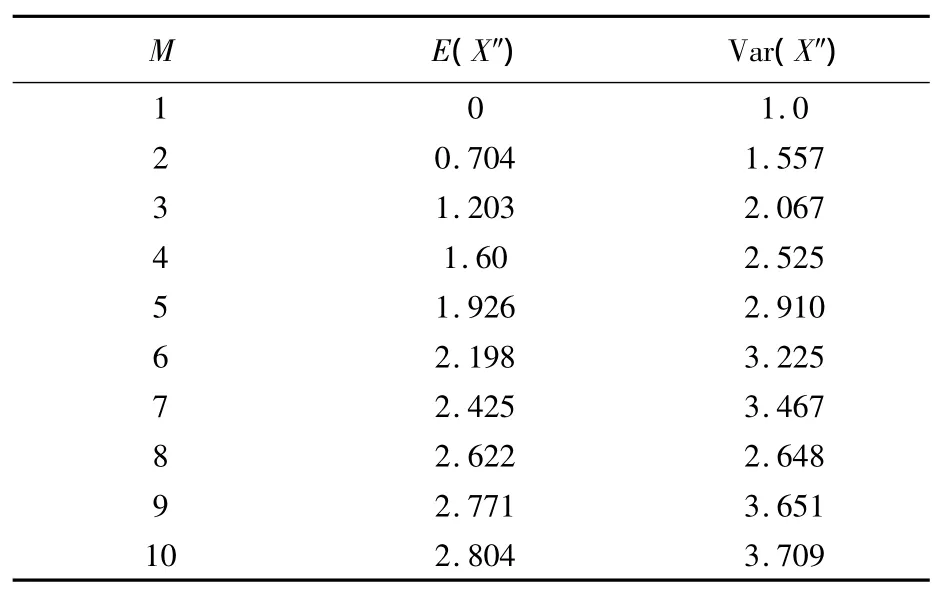
表 1 E(X″)和 Var(X″)取值

①按多细节寿命分布函数进行随机抽样，获得多细节寿命的样本点(N，PY)i(i=1，2，…，K)，其中PY=FY(N);

②按式(1)确定单细节寿命样本点(N，PX)i，其中 PX=FX(N)=1－(1－PY)1/M;

③由(N，PX)i数据对进行分布特性拟合优度检验，若单细节寿命也服从对数正态分布LN(E(X″)，Var(X″))，则有

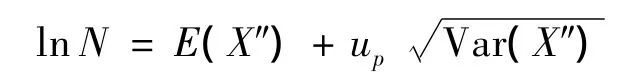
由(N，PX)i数据对构造(up，N)i数据对，按线性回归方法给出相关系数［12］.

取随机样本点数量K≥50000，相关系数均大于0.997，可以接受单细节寿命服从对数正态分布的假设.

典型细节数对应的模拟结果见图1.

图1 分布函数对比

从图1可以看出，在分布函数的首尾两端差别相对比较明显，应予以关注，典型失效概率P下对应的单细节寿命相对误差见表2.

表2 小概率对应的相对误差

取军用飞机结构常用的失效概率P=0.1%，估计值均小于真值，偏于保守.

2)寿命分布参数的关系

式(2)和表1可以作为单细节对数寿命分布的数学期望和方差.随着细节数的增加，分布函数依次右偏，说明数学期望和方差随细节数的增加而增大.

4 算例

美国空军耐久性手册背景资料给出7475-T7351铝合金双孔平板试件在随机载荷谱下的疲劳试验结果［13］，该试件两孔距离足够大保证两孔应力分布无相互影响，在试件断裂后将另一孔静拉断，通过断口判读获得裂纹萌生寿命.将两个孔的裂纹萌生尺寸为0.76mm(0.03 in)时对应的裂纹萌生寿命列入表3.

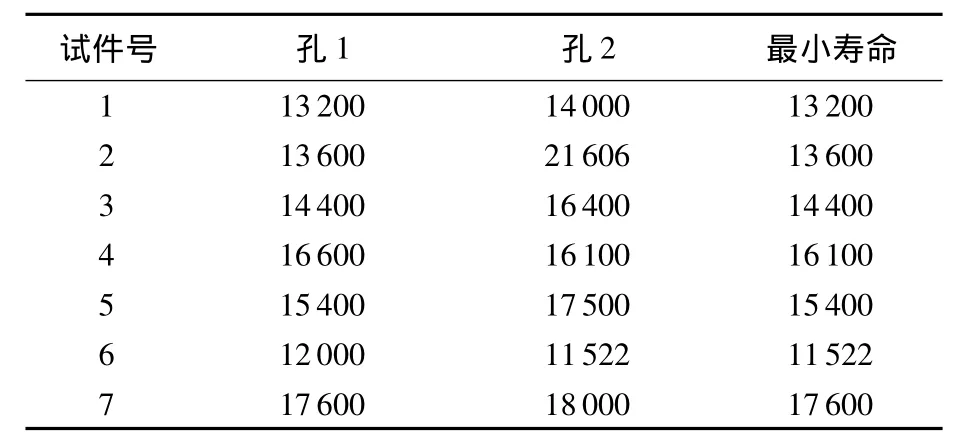
表3 双细节试件寿命 飞行小时

1) 假定试件寿命服从对数正态分布

假定试件疲劳寿命N服从对数正态分布，由表3数据按下式估计分布参数:

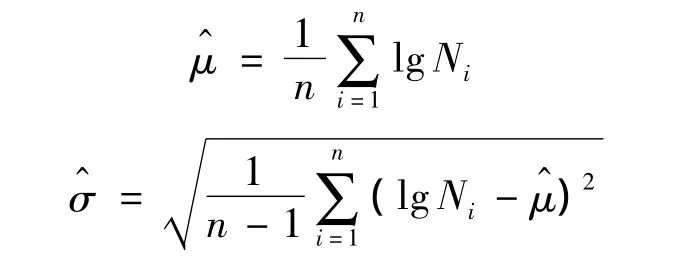
式中，n为试件数，n=7.

由表3中第4列数据估计得到双细节试件寿命分布为 LN(4.159 12，0.060 842)，将表 3 中第1、第2列数据综合在一起估计得到的单细节寿命分布为 LN(4.18612，0.074622)，按式(2)和表1，标定得到的单细节对数寿命期望为4.159 12+0.06084 ×0.7014=4.20195，方差为0.060842×1.557=0.075 922，即标定的单细节寿命服从LN(4.20195，0.075922)，对应的上述分布函数曲线见图2.

由于试件样本容量有限，估计得到的曲线与标定曲线有一定差别.但在高可靠度区，这种差别不明显.

2)假定疲劳寿命服从双参数Weibull分布

按下式估计分布参数:

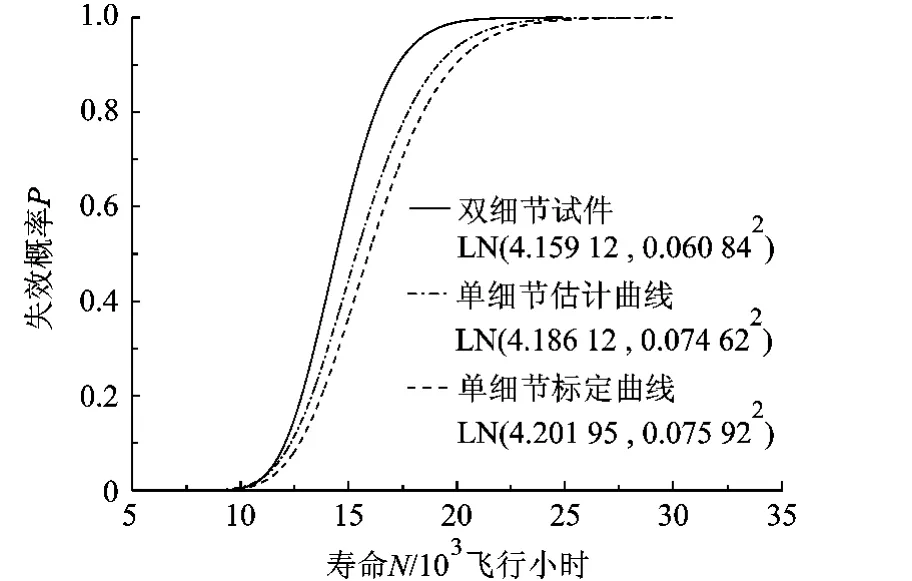
图2 分布函数对比

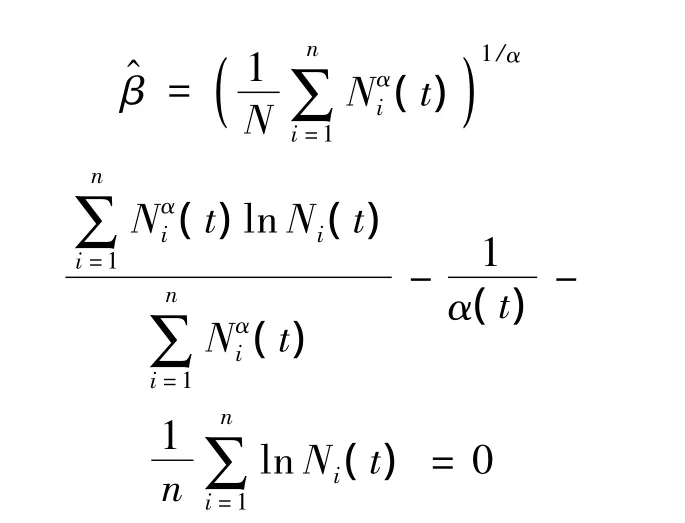
估计得到的参数分别为:双细节试件寿命服从Wei(15 372，8.657 2)、单细节寿命服从 Wei(16686，6.1492)，标定得到的单细节寿命特征值为15372 ×21/8.6572=16653，标定得到的单细节寿命服从 Wei(16653，8.6572).上述分布函数如图3所示.

图3 基于Weibull分布的对比图

同样，由于试件样本容量的限制，估计得到的尺度参数和斜率参数与标定值均不同.为了保证分布参数的稳健性，参考文献［10－11］，取多细节寿命分布斜率α=4.0，按上述过程得到:试件寿命服从Wei(14 895，4.0)、估计得到的单细节寿命服从Wei(16 219，4.0)，标定得到的单细节寿命特征值为14895×21/4.0=17713，标定得到的单细节寿命服从 Wei(17 713，4.0)，上述分布函数见图4.

同样，由于样本容量的限制，估计值与标定值有一定差别，但在高可靠度区，差别不明显.

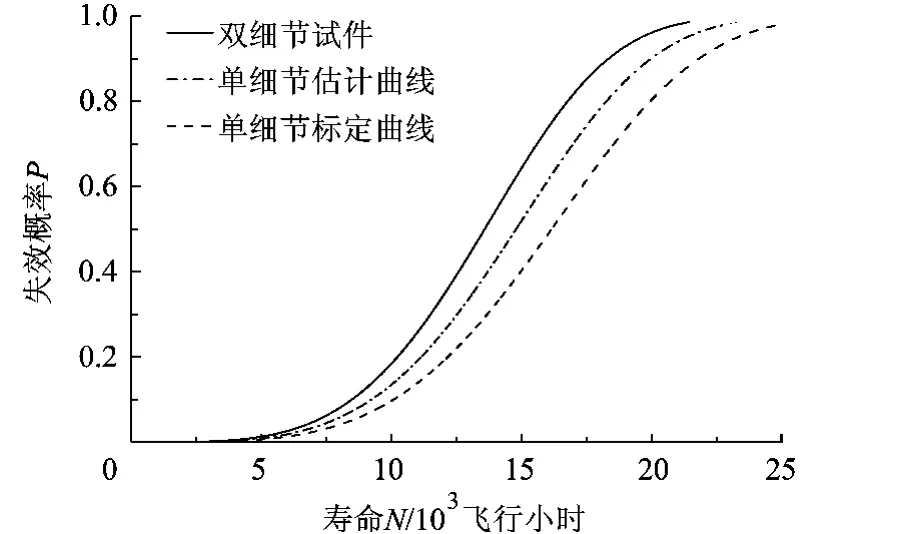
图4 基于单参数Weibull分布的对比图

5 结论

1)当多细节寿命服从对数正态分布时，单细节寿命也可近似用对数正态分布描述，但在分布函数首尾两端差别比较明显.单细节寿命分布参数与多细节寿命分布参数间存在明确关系，单细节寿命的数学期望和方差随着细节数的增加而增大.

2)当多细节寿命服从双参数威布尔分布时，单细节寿命也服从双参数威布尔分布，分布参数间也存在明确关系:分布斜率不变，位置参数按比例放大.

References)

［1］贺小帆，董彦民，阎有为，等.独立多细节结构疲劳寿命分布的数值模拟与分析［J］.工程力学，2010，27(8):217－222 He Xiaofan，Dong Yanmin，Yan Youwei，et al.Simulation and analysis of fatigue life distribution characteristic of muliti-details structures［J］.Engineering Mechanics，2010，27(8):217 － 222(in Chinese)

［2］ Schijve J.Statistical distribution functions and fatigue of structures［J］.Internantional Journal of Fatigue，2005，27:1031 －1039

［3］ WeibullW.The effect of size and stress history on fatigue crack initiation and propagation［R］.AD0287962，1962

［4］张福泽.疲劳分散系数中标准差的研究［J］.航空学报，1986，7(增刊1):17－27 Zhang Fuze.Study on the standard variation of fatigue scatter factor［J］.Acta Aeronautics et Astronautica Sinica，1986，7(Supplement1):17－27(in Chinese)

［5］施耐康.规范疲劳寿命及其标准差［J］.航空学报，1987，8(10):B467－B474 Shi Naikang.Normalize the fatigue life and standard variation［J］.Acta Aeronautics et Astronautica Sinica，1987，8(10):B467－B474(in Chinese)

［6］ DEF 00-970 Design and airworthiness requirements for service aircraft［S］

［7］ Cardrick AW，Mew A B.Scatter considerations in the interpretation ofmajor fatigue tests［C］//Rudd JL，Bader RM.Proceedings of the 20th ICAF Symposium，Volume II.Bellevue，Washington:［s.n.］，1999:14 －16

［8］高镇同.疲劳应用统计学［M］.北京:国防工业出版社，1986:375－377 Gao Zhentong.Applied statistics of fatigue［M］.Beijing:Chinese National Defense Industry Press，1986:375 －377(in Chinese)

［9］ Whittaker IC，Besuner PM.A reliability analysis approach to fatigue life of aircraft structures［R］.AD-853263，1969

［10］ Whittaker IC.Development of Titanium and steel fatigue variability model for application of reliability analysis approach to aircraft structures［R］.AD-758219，1972

［11］刘文珽，郑旻仲，费斌军.概率断裂力学与概率损伤容限/耐久性［M］.北京:北京航空航天大学出版社，1999:47－49 Liu Wenting，Zheng Minzhong，Fei Binjun.Probabilistic fracture mechanics and probabilistic damage tolerance/duration［M］.Beijing:Press of Beijing University of Aeronautics and Astronautics，1999:47 －49(in Chinese)

［12］ Manning SD，Pendley B J，Garver W R，et al.美国空军耐久性设计手册背景材料［M］.航空航天部(AFFD)系统工程办公室译.北京:AFFD系统办公室，1987:B135－B137 Manning SD，Pendley B J，Garver W R，et al.Background information of USAF durability design handbook［M］.Translated by AFFD Systems Engineering Office.Beijing:AFFD Systems Engineering Office，1987:B135 － B137(in Chinese)

(编 辑:李 晶)

Statistical scaling of durability life for independent multi-detail structures

He Xiaofan Dong Yanmin Liu Yanmao Liu Wenting

(School of Aeronautic Science and Engineering，Beijing University of Aeronautics and Astronautics，Beijing 100191，China)

To assess the fatigue life for aircraft structure，the specimen used for the durability test is often designed as multi-details(MD)to simulate the structural configuration and load transfer.Once one detail fails，the fatigue testing is ended，and the fatigue life of single detail(SD)must be deduced statistically based on the incomplete life of MD specimen.Based on the series failure model of the same multi-detail structures，the statistical scaling approach was proposed to determine the life distribution of the single detail.Assuming the fatigue life of MD follows the log-normal distribution，Monte Carlo sampling and stimulating results show that the fatigue life of single detail follows the same distribution approximately;the expressions between the distribution parameters of MD and SD are deduced.The expectation and variation of MD are higher than those of SD.Assuming the fatigue life of MD follows the two-parameter Weibull distribution，the SD’s fatigue life follows the same distribution whose slope is unchanged，but location parameter is larger than that of MD.Finally，an example for analyzing MD fatigue test result from American durability test program is given.

fatigue;service life;multi-details;log-normal;Weibull distribution;statistical scaling

V 215.5

A

1001-5965(2012)06-0715-05

2011-03-15;网络出版时间:2012-06-15 15:44

www.cnki.net/kcms/detail/11.2625.V.20120615.1544.030.htm l

国家自然科学基金资助项目(11002009)

贺小帆(1976 －)，男，湖北天门人，副教授，xfhe@buaa.edu.cn.